Ключевые слова: угол, окружность, хорда, дуга, центральный угол, вписанный угол, касательная, секущая, теорема о секущих, теорема о касательной и секущей, градусная мера дуги, угол опирается на хорду, угол опирается на дугу, дуга стягивает хорду, угол между хордой и касательной, внутренный угол окружности, внешний угол окружности.
Центральные и вписанные углы в окружности
Центральный угол в окружности - угол с вершиной в ее центре и сторонами-радиусами.
Дуга окружности , соответствующей центральному углу - часть окружности внутри плоского угла.
Градусная мера дуги окружности - градусная мера соответствующего центрального угла.
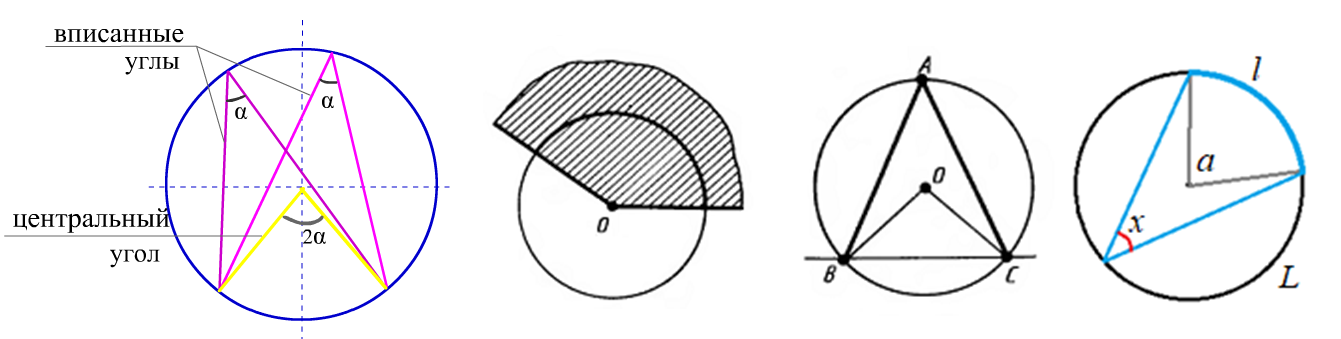
Вписанный угол - вершина которого лежит на окружности, а стороны пересекают эту окружность (хорды).
- Вписанный угол опирается на хорду , которая соединяет точки пересечения сторон угла и окружности.
- Вписанный угол опирается на дугу, заключенную между его сторонами.
- Обозначение: $AB^o$ - градусная мера дуги $AB$ , равна центральному углу $AOB$.
Теорема Вписанный угол равен половине того центрального угла, что опирается на ту же дугу.
Теорема$\angle BAC=\frac{\angle BOC}{2}=\frac{BC^o}{2}$ $\angle BAD=\frac{\angle BOD}{2}=\frac{BD^o}{2}$ $\angle DAC=\frac{\angle DOC}{2}=\frac{DC^o}{2}$



Случай 1: Точка $O$ принадлежит лучу $AC$.
- Пусть $\angle A = \alpha$ , тогда и $\angle B = \alpha$ , ведь $\bigtriangleup AOB$ - равнобедренный, его стороны $OB=OA$ как радиусы.
- $\angle BOC$ является внешним для треугольника , а значит равен сумме двух других углов: $\alpha+\alpha=2\alpha$
- угловое измерение дуги $BC$ есть $2\alpha$ $\Rightarrow$ вписанный угол равен половине дуги, на которую он опирается.
Случай 2: Точка $O$ лежит внутри вписанного угла $\angle BAC$ .
- Проведем диаметр $AD$, обозначим $\angle BAD = \alpha$ и тогда дуга $BD$ равна $2\alpha$ (см. случай 1).
- Обозначим $\angle BAD$ за $\beta$ , тогда дуга $DC$ равна $2\beta$ ( так же из-за случая 1)
- $\Rightarrow$ вся дуга $BC = 2\alpha + 2\beta = 2\left(\alpha+\beta\right)$. Но $\angle BAC$ , в свою очередь, равен $\alpha + \beta$
- $\Rightarrow$ вписанный угол равен половине дуги, на которую он опирается.
Случай 3: Точка $O$ находится вне вписанного угла .
- Проведем диаметр $AD$, обозначим угол $\angle BAD$ через $\alpha$ , тогда дуга $BD$ равна $2\alpha$ (из-за случай 1).
- $\angle CAD$ обозначим через $\beta$ , тогда дуга $DC = 2\beta$ (из-за случай 1).
- Дуга $BC$ является разностью большой дуги $BD$ и дуги $DC$ : $BC=BD-DC=2\alpha-2\beta=2\left(\alpha-\beta\right)$
- $\Rightarrow$ Вписанный угол $\angle BAD = \alpha - \beta$. ... вписанный угол равен половине дуги опирания.
Следствия теоремы о вписанном угле:
- Все вписанные углы, стороны которых проходят через $A$ и $B$, вершины лежат по одну сторону от прямой $AB$ , равны.
- Все вписанные углы, опирающиеся на одну и ту же дугу, равны меж собой.
- Вписанные углы, опирающиеся на диаметр, равны 90° , являются прямыми углами....центральный угол 180° .
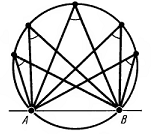
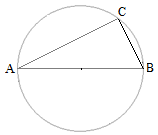
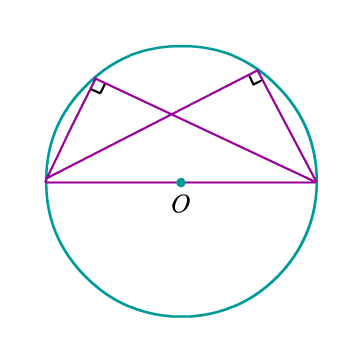
Задача 1: Точки $A$, $B$, $C$ находятся на окружности и делят ее на три дуги, градусные величины которых относятся как 1 : 3 : 5. Найдите больший угол треугольника $ABC$ в градусах.
- Решение: Пусть меньшая дуга окружности равна $x$ , тогда $x + 3x + 5x = 360^o$ , $9x = 360^o$ , $x = 40^o$
- Больший угол $\bigtriangleup ABC$ опирается на большую дугу и равен $5\cdot40^o$ , для окружности он является вписанным
- и значит равен половине этой дуги $\frac{200}{2}$. Ответ: $100^o$
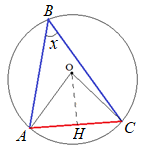
Задача 2: В треугольнике $ABC$ угол $B$ равен $25^o$ . Найти угол между радиусом описанной окружности и противоположной стороной $AC$.
- Решение: Обозначим $\angle ABC$ за $x$ . Он вписанный и опирается на дугу $AC$ , на которую так же опирается центральный угол $AOC$.
- Вписанный угол в два раза меньше центрального $\Rightarrow$ $\angle AOC = 2x$.
- $\bigtriangleup AOC$ - равнобедренный, т.к. две его стороны являются радиусами ,
- значит углы при основании - хорде $AC$ равны и $OAC=OCA=\frac{180-2x}{2}=90-x=90-25=65$ .
- Кстати, угол $HOC=ABC=x$. Ответ: $65^o$
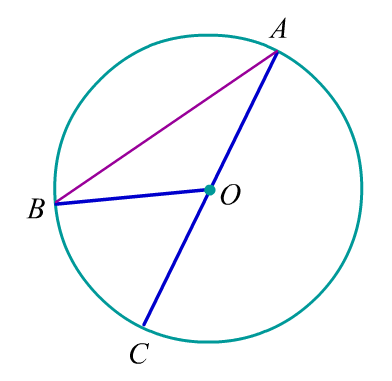
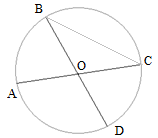
Задача 3: Отрезки $AC$ и $BD$ — диаметры окружности с центром $O$ , образовали меж собой угол $COD$ равный $58^o$. Найти $\angle ACB$.
- Решение: Углы $BOA$ и $COD$ равны как вертикальные , поэтому $\angle BOA = 58^o$ .
- Искомый угол $ACB$ - вписанный и он опирается на ту же дугу , что и центральный угол $BOA$ .
- По теореме о вписанных и центральных углах $ACB=\frac{1}{2}BOA=\frac{1}{2}\cdot58=29$ Ответ: $\angle ACB = 29^o$
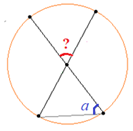
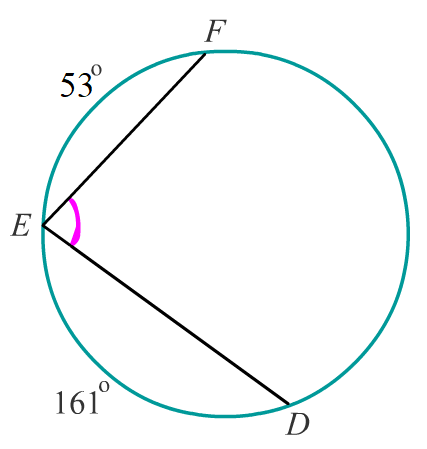
Задача 4: Найдите $\angle DEF$, если градусные меры дуг $DE$ и $EF$ равны $161^o$ и $53^o$ соответственно.
- Решение: $\angle DEF$ — вписанный, его градусная мера равна половине дуги, на которую он опирается.
- Дуга $FD = 360° – (161° + 53°) = 146°$ $\Rightarrow$ $\angle$ $DEF=\frac{1}{2}146=73$ Ответ: $73^o$
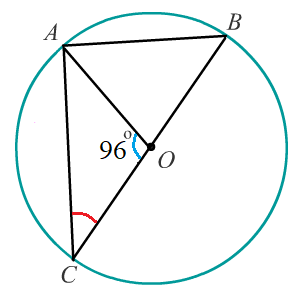
Задача 5: Найдите градусную меру $\angle ACB$ , если известно, что $BC$ является диаметром окружности, а градусная мера центрального $\angle AOC$ равна $96^o$.
- Решение: $\angle ACB$ — вписанный, опирается на дугу $AB$ и равен её половине. Найдем дугу $AB$.
- $BC$ — диаметр окружности, дуга $CAB$ равна $180^o$. $\angle AOC$ - центральный угол. По условию $\angle AOC = 96^o$ .
- $\Rightarrow$ дуга $AC = 96^o$ , а дуга $AB = 180^o - 96^o = 84^o$ , тогда $\angle$ $ACB=\frac{1}{2}84=42$. Ответ: $\angle ACB = 42^o$
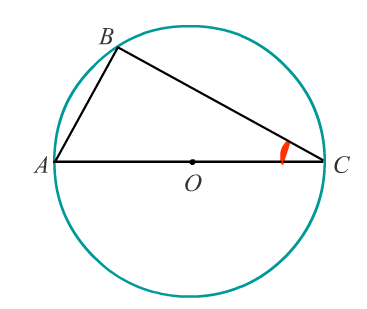
Задача 6: Сторона $AC$ треугольника $ABC$ содержит центр описанной около него окружности. Найдите $\angle C$, если $\angle A = 69^o$.
- Решение: Важное свойство: вписанный $\angle В$ , опирающийся на диаметр $AC$ , равен $90^o$ .
- Любой диаметр - развернутый центральный угол - опирается на дугу $180^o$ $\Rightarrow$ $\bigtriangleup ABC$ — прямоугольный.
- По свойству прямоугольного треугольника сумма острых углов равна $90^o$ $\Rightarrow$ $\angle C=90^o-\angle A=90^o - 69^o=21^o$ .
- Ответ: $\angle C = 21^o$
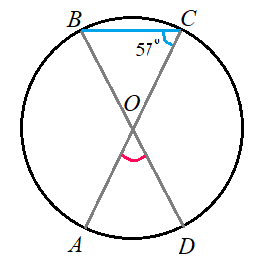
Задача 7: $AC$ и $BD$ — диаметры окружности с центром $O$. $\angle ACB$ равен $57^o$. Найдите $\angle AOD$ .
- Решение: $\angle ACB$ является вписанным углом , значит равен половине дуги, на которую опирается ...
- градусная мера дуги $AB= 2B = 2\cdot57^o=114^o$ . $O$ — центр окружности лежит на $BD$ , значит $BAD = 180^o$,
- тогда дуга $AD = 180^o - 114^o= 66^o$. $\angle AOD$ — центральный и опирается на дугу $AD$ ,
- значит их градусные меры совпадают. $\Rightarrow$ Ответ: $\angle AOD = 66^o$
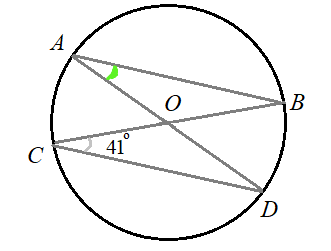
Задача 8: В окружности с центром в точке $O$ проведены диаметры $AD$ и $BC$ , угол $OCD$ равен $41^o$. Найдите величину $\angle OAB$ .
- Решение: $\angle OCD$ и $\angle OAB$ — вписанные и опираются на одну и ту же дугу $DB$ , тогда ...
- ... по свойству вписанных углов они равны. Таким образом, $\angle OAB$ то же равен $41^o$. Ответ: $\angle OAB = 41^o$
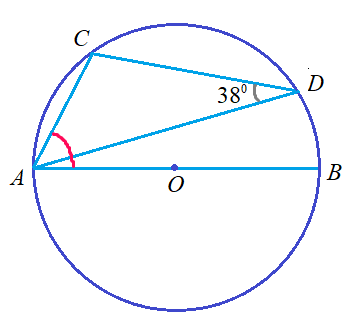
Задача 9: Диаметр $AB$, угол $CDA$ равен 38°. Найдите величину угла $CAB$.
- Решение: угол $CDA$ - вписанный, значит его дуга $AC^o=2\cdot38^o=76^o$. Тогда дуга $BCD$ равна $180 - 76 = 104^o$ ,
- но на нее опирается вписанный угол $CAB$ $\Rightarrow$ $CAB=\frac{1}{2}104^o$ Ответ: $CAB = 52^o$
О главном по теме: Центральные и вписанные углы в окружности. 1. Центральный угол в окружности - угол с вершиной в ее центре и сторонами-радиусами. 2. Дуга окружности , соответствующей центральному углу - часть окружности внутри плоского угла. 3. Градусная мера дуги окружности - градусная мера соответствующего центрального угла. 4. Вписанный угол - вершина которого лежит на окружности, а стороны пересекают эту окружность (хорды). .... Вписанный угол опирается на хорду , которая соединяет точки пересечения сторон угла и окружности. .... Вписанный угол опирается на дугу, заключенную между его сторонами. Теорема Вписанный угол равен половине того центрального угла, которая опирается на ту же дугу.
Решаем устно:

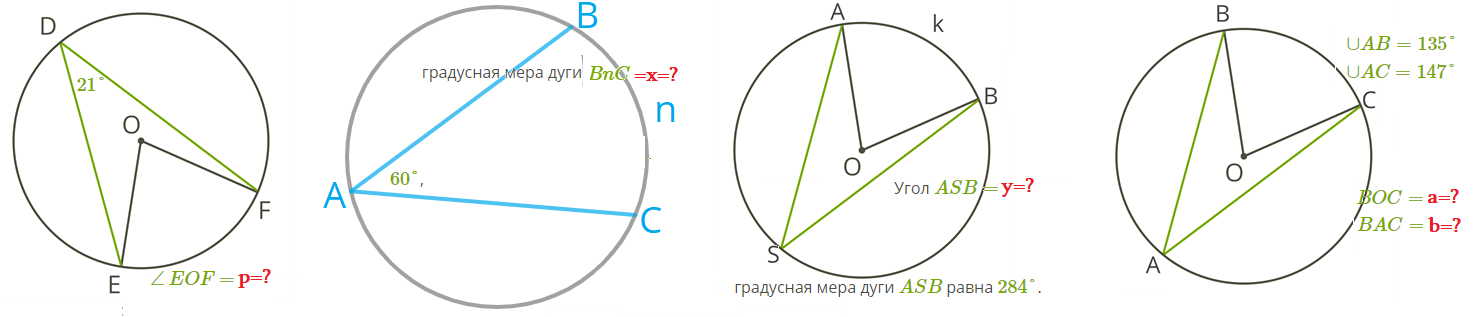
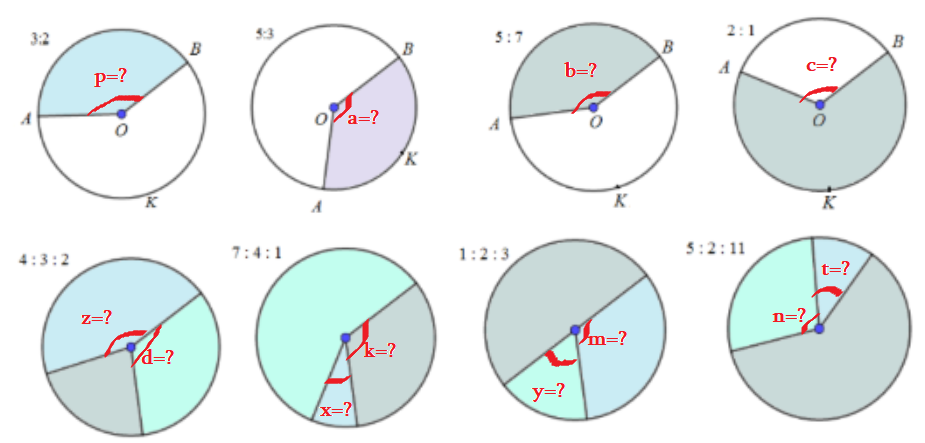
Упражнения (А):
Упражнения (В):

Задачи из сайта https://resh.edu.ru :
Задача 21: Угол АВС равен 66. Найти все что можно. (Т)
Задача 22: Градусные меры дуг окружности относятся как 3 : 2 : 2 : 5. Найдите градусную меру большей из этих дуг.
Задача 23: Точки А, В, С, D отметили на окружности в порядке следования их в латинском алфавите. При этом оказалось, что дуга ВСD в 3 раза больше дуги BАD. Найдите градусную меру дуги BCD.
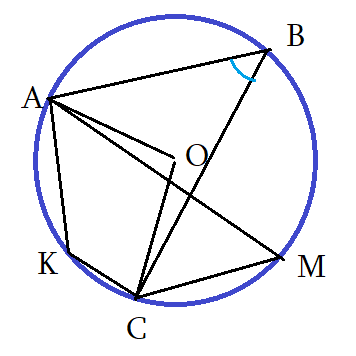
Задача 24: В окружности с центром О проведены две равные хорды MK и PN. Найдите градусную меру большей из дуг с концами M и K, если угол PON равен 110°
Задача 25: Вписанный угол CBA равен 80°, где AB – диаметр. Найдите угол CAB.
Задача 26: На окружности с центром в точке O взяли последовательно точки A, B, C так, что ∠AOC = 150°. Найдите градусную меру угла ABC.
Задача 27: Точки А, В и С лежат на окружности с центром О, ∠ВАС – вписанный угол. Про градусные меры дуг известно, что ∪AB : ∪BC : ∪AC = 3 : 1 : 2. Найдите АВС.
Задача 28: В окружности проведен диаметр AB и равные хорды AC и AD так, что ∠DAB = 40°. Найдите градусную меру угла CBD.
Задача 29: Три точки A,B,C делят окружность на части так, что ∪AB : ∪BC : ∪AC = 3 : 4 : 5. Найдите градусные меры из этих дуг.
Задача 30: Дана окружность с центром в точке О. На окружности взяты точки N, P, Q так, что угол РОQ в 2 раза меньше угла PON и в 3 раза меньше угла QON. Найдите градусную меру дуги PQ, которая не содержит точку N.
Задача 31: Вписанный угол ВСD равен 25°, дуга ВС имеет градусную меру 80°. Найдите градусную меру дуги CD.
Задача 32: На окружности взяли последовательно точки A, B, C, D так, что ∠ABC = 120°. Найдите градусную меру угла ADC.
Задача 33: На окружности с центром в точке О взяты точки K, М, N так, что MK – диаметр, а угол КОN равен 80°. Найдите угол КМN.
