Ключевые слова: угол, окружность, хорда, дуга, центральный угол, вписанный угол, касательная, секущая, теорема о секущих, теорема о касательной и секущей, градусная мера дуги, угол опирается на хорду, угол опирается на дугу, дуга стягивает хорду, угол между хордой и касательной, внутренный угол окружности, внешний угол окружности.
Внешний угол треугольника - угол, образованный между стороной и продолжением соседней стороны треугольника. Внешний угол треугольника = сумме двух внутренних углов треугольника, несмежных с ним. Если у треугольников одинаковый состав углов, то такие треугольники подобны ... стороны пропорциональны.
Центральный, вписанный угол и их стягивающие дуги
- Центральный угол: вершина - центр окружности, а стороны - радиусами
- Градусной мерой дуги является величина центрального угла, опирающегося на эту дугу.

- Вписанный угол — вершина лежит на окружности, а стороны пересекают эту окружность (хорды).
- Вписанный угол равен половине того центрального угла, что опирается на ту же дугу.
- Вписанный угол равен половине градусной меры той дуги, на которую опирается.
- Формулы Теорема$\angle BAC=\frac{\angle BOC}{2}=\frac{BC^o}{2}$ $\angle BAD=\frac{\angle BOD}{2}=\frac{BD^o}{2}$ $\angle DAC=\frac{\angle DOC}{2}=\frac{DC^o}{2}$

- Вписанный угол, опирающийся на диаметр, равен 90° ... $\bigtriangleup$ - прямоугольный. И наоборот!
- Все вписанные углы, опирающиеся на одну и ту же дугу, равны меж собой.
- О пропорциях: окружность поделена на дуги в отношении 5 : 8 : 12 , то дуги равны 5х, 8х, 12х

Пересечение хорд $\to$ внутренний угол $\to$ зажатые дуги
- Внутренний угол окружности - угол, образованный двумя хордами, вершина внутри окружности.
- Внутренний угол м\ж хордами равен половине суммы дуг, отсеченных этими хордами.
- ... Образованные треугольники, соприкасающиеся в точке пересечения, попарно подобны.

Секущие из одной точки $\to$ внешний угол $\to$ заключенные м\ж ними Дуги
- Внешний угол окружности - угол, образованный двумя секущими, вершина вне окружности.
- Угол м\ж двумя секущими из одной точки, равен половине разности дуг, заключенными м\ж ними.
- ..... возникают пары подобных треугольников, с переворачиванием ....

Угол между касательной и хордой (секущей, касательной, радиусом) :
- Касательная пересекается с окружностью в 1-ой точке ... касания; "как секущая с 1-ой точкой".
- Угол м\ж касательной и радиусом в точке касания равен $90^o$, перпендикулярны!.
- Угол м\ж касательной и секущей из одной точки, равен половине разности дуг, заключенных м\ж ними.
- Угол м\ж касательной и хордой в точке на окружности, равен половине дуги, зажатой м\ж ними.
- Угол м\ж двумя касательными из одной точки, равен полуразности дуг, заключенных м\ж ними.

Углов много, дуг мало $\to$ ищи равные углы $\to$ ищи подобия ...
Еще, факты. 1. Радиус и касательная образуют прямоугольный треугольник. 2. Если хорды равноудалены от центра окружности, то они равны. 3. Если хорды равны, то они равноудалены от центра окружности. 3. Большая из двух хорд находится ближе к центру окружности. 4. Наибольшая хорда является диаметром. 5. Если диаметр делит хорду пополам, то он перпендикулярен ей. 6. Если диаметр перпендикулярен хорде, то он делит ее пополам . 7. Равные дуги стягиваются равными хордами. 8. Дуги, заключенные между параллельными хордами, равны. 9. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны. 10. Все вписанные углы, опирающиеся на диаметр прямые. 11. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180∘
Главное: Центральный = дуге ; Вписанний = половине дуги ; Внутренний = полусумме 2-х дуг ; Внешний = полуразности 2 - х дуг ; Угол м\ж касательной и секущей = полуразности 2 - х дуг ; (м\ж двумя касательными - так же!) ; Угол м\ж касательной и хордой = половине дуги ; Угол м\ж касательной и радиусом = 90 град ;

Углубление: более подробно см. параграфы по отдельным темам
XIII . §45 Дуги в Окружности: Центральный угол.
XIII . §46 Вписанные углы в окружности.
XIII . §48. Пересекающиеся Хорды в окружности. Внутренний угол
XIII . §50. Секущие из Одной Точки. Внешний Угол
XIII . §52. Касательные к Окружности
XIII . §53. Теорема о Касательной и Секущей из Одной Точки
XIII . §54. Угол между Касательной и Хордой из Одной Точки

Упражнения (А): Тренинг по понятиям, свойствам, формулам
Упражнения (В): задачи по теме: контрольно-экзаменационные
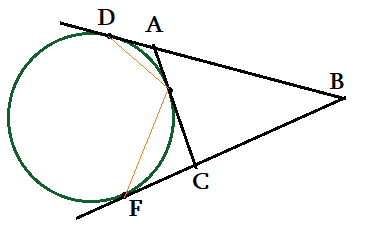
Задача 6: Дан остроугольный $\bigtriangleup ABC$ и окружность, которая касается его стороны $AC$ и продолжения сторон $BA$ и $BC$ в точках $E$, $D$ и $F$ соответственно. Докажите, что $DEF=90+\frac{ABC}{2}$
- $AED+DEF+CEF=180^o$, т.к все вместе эти углы составляют развернутый угол $\Rightarrow$ $DEF=180^o-AED-CEF$
- $AD$ и $AE$ - касательные, проведенные к окружности из одной точки,
- значит по правилу равенства отрезков таких касательных $AD=AE$ $\Rightarrow$ $\bigtriangleup DAE$ - равнобедренный
- и углы при основании равны: $\angle ADE = \angle AED$ .
- $\angle BAC$ - внешний угол для $\bigtriangleup DAE$ . Применим для этого треугольника правило:
- внешний угол $\bigtriangleup$ равен сумме двух углов этого $\bigtriangleup$ , несмежных с ним
- получаем $BAC=ADE+AED$ и , учитывая равенство углов , получим $\angle AED=\frac{\angle BAC}{2}$.
- $\bigtriangleup FCE$ - тоже равнобедренный , ведь $CE = CF$ как отрезки касательных.
- Углы $CEF$ и $CFE$ равны. Угол $ВСА$ внешний к треугольнику $FCE$, значит
- $BCA=CEF+CFE$ . ... $BCA=2\cdot CEF$ $\Rightarrow$
- $DEF=180-\frac{BAC+BCA}{2}$ . Из суммы углов в $\bigtriangleup ABC$ произведем замену в числителе ,
- разделим почленно числитель на знаменатель: $DEF=90+\frac{ABC}{2}$ . Что и требовалось доказать.
Упражнения (C): задачи повышенной сложности




