Ромб - это параллелограмм, у которого все стороны равны.
- "Чтоб Выучить, распознать нечто стоящее - узнать его в движении, при изменениях"
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей - ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали - новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали - ромб совпадает с самим собой. Симметрия.
Замечание: Если "зряче видим" центральную и осевые симметрии ромба, то все его свойства у нас "в кармане".
Свойства ромба:
- Ромб симметричен относительно точки O - пересечения диагоналей. O - центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ - ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
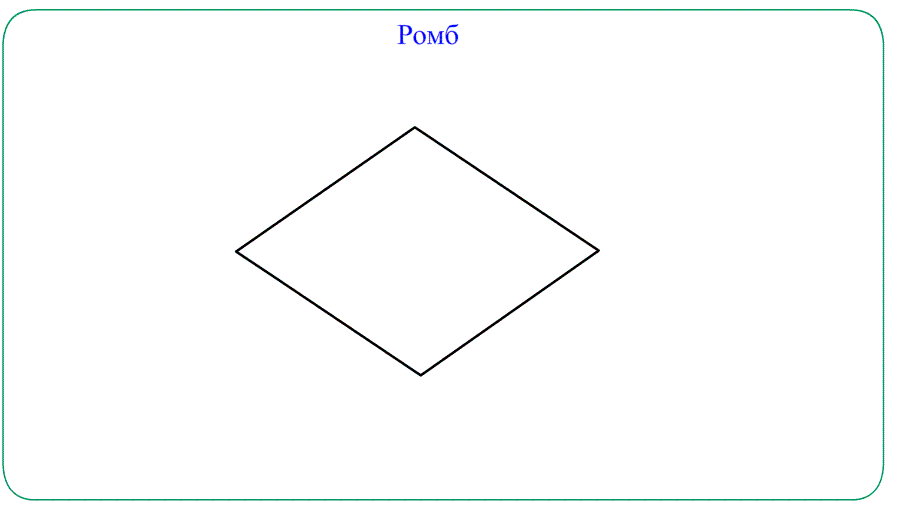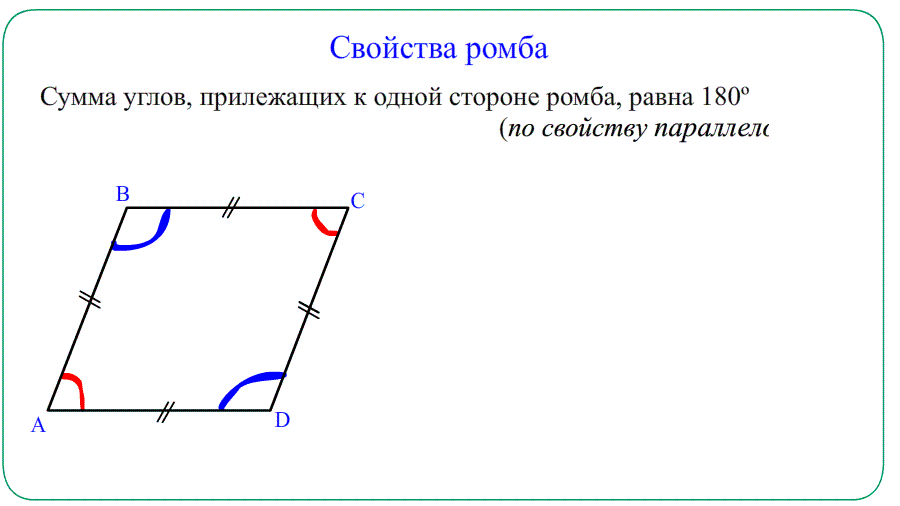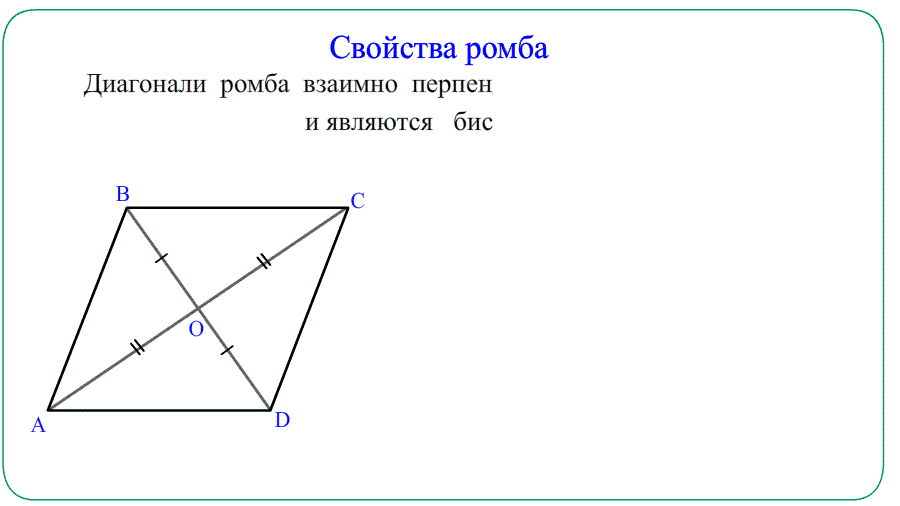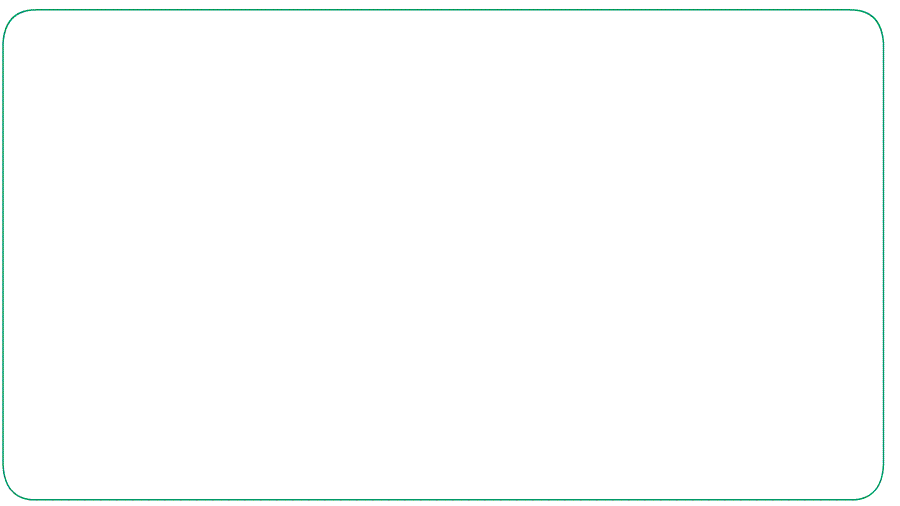
- Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов - делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2\cdot a\cdot b\cdot\cos D$ , большая - $BD^2=a^2+b^2+2\cdot a\cdot b\cdot\cos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4\cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=AD\cdot CH$ , $S=a\cdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2\cdot\sin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=\frac{AC\cdot BD}{2}$ . - половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если ... суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=p\cdot r$, $p=2\cdot a$ $S=2\cdot a \cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали - суть биссектрисы углов.
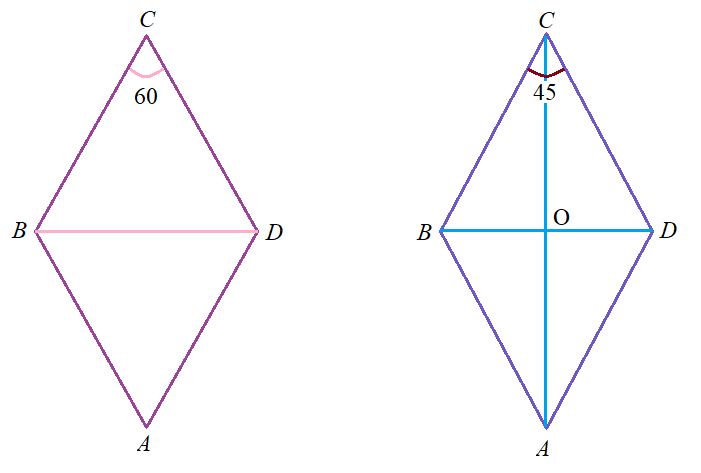
Задача 1: Найти периметр ромба $ABCD$, в котором $\angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $\bigtriangleup BCD$. Что в нём равного? $\Rightarrow$ каков данный треугольник?
- По условию, угол $\bigtriangleup BCD$ у вершине $\angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: "Односторонние углы": В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30'$ , $67^o30'$
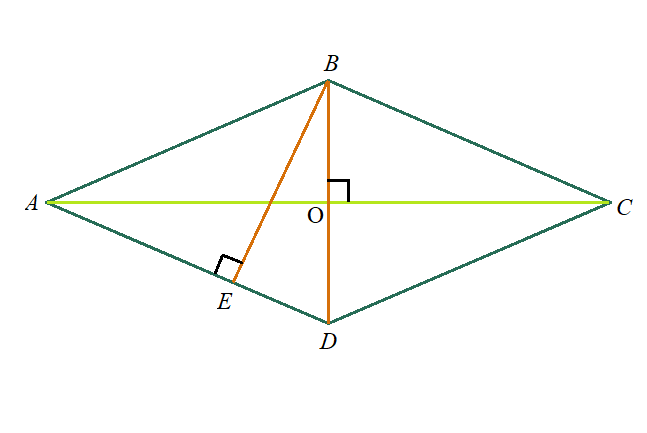
Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $\bigtriangleup BED \sim \bigtriangleup AOD=\bigtriangleup AOB=\bigtriangleup COB=\bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $\alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $\alpha$ в $\bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $\Rightarrow$ $\sin\alpha=\frac{BE}{BD}=\frac{12}{13}$
- Перейдем к $\bigtriangleup OCD$ : в нем прилежащий катет $OD=\frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $\sin^2\alpha+\cos^2\alpha=1$ . Тогда косинус: $\cos\alpha=\pm\sqrt{1-\sin^2\alpha}=\pm\sqrt{1-\frac{144}{169}}=\pm\sqrt{\frac{25}{169}}=\pm\frac{5}{13}$
- Угол $\alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $\cos\alpha = \frac{5}{13}$
- Тогда: $\frac{DO}{DC}=\frac{6,5}{DC}=\cos\alpha=\frac{5}{13}$ $\Rightarrow$ $DC=\frac{6,5\cdot13}{5}=\frac{13\cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9\cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ - пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
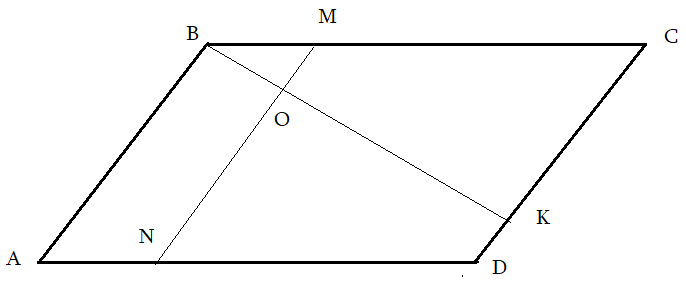
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ - параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ - квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $\Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб - это параллелограмм, у которого все стороны равны.
- "Чтоб Выучить, распознать нечто стоящее - узнать его в движении, при изменениях"
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей - ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали - новый ромб совпадет с прежним. Симметрия.
Замечание: Если "зряче видим" центральную и осевые симметрии ромба, то все его свойства у нас "в кармане".
Свойства ромба:
- Ромб симметричен относительно точки O - пересечения диагоналей. O - центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ - ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов - делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2\cdot a\cdot b\cdot\cos D$ , большая - $BD^2=a^2+b^2+2\cdot a\cdot b\cdot\cos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4\cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=AD\cdot CH$ , $S=a\cdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2\cdot\sin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=\frac{AC\cdot BD}{2}$ . - половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если ... суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=p\cdot r$, $p=2\cdot a$ $S=2\cdot a \cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали - суть биссектрисы углов.
Задача 1: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: "Односторонние углы": В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30'$ , $67^o30'$


Задача 2: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $\bigtriangleup BED \sim \bigtriangleup AOD=\bigtriangleup AOB=\bigtriangleup COB=\bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $\alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $\alpha$ в $\bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $\Rightarrow$ $\sin\alpha=\frac{BE}{BD}=\frac{12}{13}$
- Перейдем к $\bigtriangleup OCD$ : в нем прилежащий катет $OD=\frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $\sin^2\alpha+\cos^2\alpha=1$ . Тогда косинус: $\cos\alpha=\pm\sqrt{1-\sin^2\alpha}=\pm\sqrt{1-\frac{144}{169}}=\pm\sqrt{\frac{25}{169}}=\pm\frac{5}{13}$
- Угол $\alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $\cos\alpha = \frac{5}{13}$
- Тогда: $\frac{DO}{DC}=\frac{6,5}{DC}=\cos\alpha=\frac{5}{13}$ $\Rightarrow$ $DC=\frac{6,5\cdot13}{5}=\frac{13\cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9\cdot12=202,8$
Задача 3: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ - пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.

Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ - параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ - квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $\Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
preHistory, repeat:
- Cвойство аддитивности: Площадь целой фигуры равна сумме площадей его кусков
- Площадь параллелограмма $S=a\cdot h$ - произведение основания на высоту
- Площадь любого треугольника $S_{ABC}=\frac{a\cdot h}{2}$ - половина произведения любой высоты на свою сторону.
- Формула Герона: Площадь треугольника через стороны с включением полупериметра
$S=\sqrt{p\cdot\left(p-a\right)\cdot\left(p-b\right)\cdot\left(p-c\right)}$ , где полупериметр $p=\frac{1}{2}\cdot\left(a+b+c\right)$ - "О прямоугольном с $30^o$": катет напротив этого угла равен половине гипотенузы. $a=\frac{c}{2}$ ; $b=\frac{\sqrt{3}}{2}c$ .
- "О прямоугольном с $45^o$": $\bigtriangleup$ - равнобедренным ; Гипотенуза: $c=\sqrt{2}a$ . Катет: $a=b=\frac{\sqrt{2}}{2}c$
XIII . §17. Свойства: параллелограмм, ромб, квадрат, прямоугольник
XIII . §21. Площадь треугольника. Формула Герона.
XIII . §16. Прямоугольный треугольник; 30 градусов, 45 градусов.
Ромб - это параллелограмм, у которого все стороны равны.
Свойства ромба очевидны по центральным и осевым симметриям: поворот на 180 градусов вокруг точки пересечения диагоналей, зеркальное отражение по диагоналям.
Свойства ромба: 1. Стороны равны $AB=BC=CD=DA=a$. 2. Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . 3. Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$. 4. Диагонали ромба точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$. 5. Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники. 6. Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники. 7. Диагонали ромба являются биссектрисами углов - делят углы пополам. 8. Диагонали ромба со сторонами образуют равные накрест лежащие углы. 9. Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Квадрат - одновременно прямоугольник, ромб, параллелограмм. Диагонали равны ... и делятся пополам.
Theo: Площадь ромба $s=AD\cdot h$ - произведение стороны (любой) на высоту (свою)
Theo: Площадь квадрата (фигуры) $s=AB^2$ - квадрату (алгебраическому) стороны
Theo: Площадь ромба $s=\frac{1}{2} AC\cdot BD$ - половине произведения диагоналей ромба
- Ромб - частный случай параллелограмма ... поэтому формула площади та же!
- Диагонали ромба делятся пополам и делят ромб на 4 прямоугольных одинаковых треугольника ...
- ... площадь ромба = четырежды половина произведения катетов (половинок диагоналей).
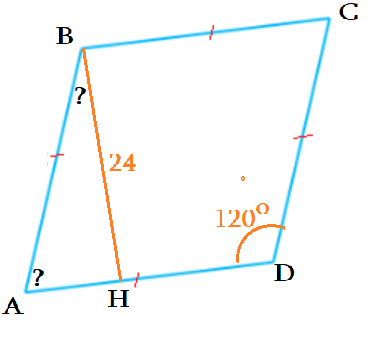
Задача 1: В ромбе $ABCD$ высота равна $24$, тупой угол $120^o$. Найдите площадь ромба.
- Тупые углы: $\angle ADC=\angle ABC=120^o$ . Острые углы, по односторонности, $\angle BAD=\angle BCD=180^o-120^o=60^o$
- Проведем высоту $BH=24$ и рассмотрим $\bigtriangleup ABH$ : прямоугольный с углом $30^o$, $\angle BAH=30^o$
- ∠30°,∠°90 $\to$ $AH=\frac{AB}{2}$, Пифагор $AB^2=24^2+(\frac{AB}{2})^2$ Сторона ромба: $AB=16\sqrt{3}=AD$
- Площадь = сторона (на) высоту: $s=S_{ABCD}=AD\cdot BH=16\sqrt{3} \cdot 24=384\sqrt{3}$
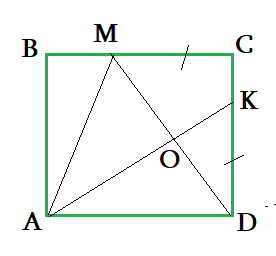
Задача 2: На сторонах ВС и CD квадрата ABCD отмечены точки М и К соответственно, MC = KD. Известно, что АВ = 5, ∠МАВ = 30° . Найдите площадь четырехугольника АМСК.
- Площадь четырехугольника АМСК найдем через вычитание площадей $S_{AMCK}=S_{ABCD}-S_{ABM}-S_{AKD}$
- $\bigtriangleup ABM$ - прямоугольный, $\angle MAB=30^o$ $\Rightarrow$ свойство 30° $AM=2BM$. Пифагор: $5^2+BM^2=(2BM)^2$ $\Rightarrow$ $BM=5\sqrt{3}$
- Найдем отрезки: $MC=AB-BM=5-5\sqrt{3}$ $\Rightarrow$ из условия $KD=MC=5-5\sqrt{3}$
- $S_{ABM}=\frac{1}{2}\cdot AB\cdot BM=\frac{25}{2} \sqrt{3}$ $S_{AKD}=\frac{1}{2}\cdot AD\cdot KD=\frac{25}{2} (1-\sqrt{3})$ $S_{ABCD}=AB^2=25$
- Требуемая площадь: $S_{AMCK}=S_{ABCD}-S_{ABM}-S_{AKD}=25-\frac{25}{2} \sqrt{3}-\frac{25}{2} (1-\sqrt{3})=\frac{25}{2}$
- Еще: 1. $\bigtriangleup DMC=\bigtriangleup AKD$ $\Rightarrow$ $\angle KAD=\angle MDC$ тогда: $\angle KAD+\angle MDA=90^o$ значит, $MD\perp AK$. Т.е. равенство отрезков MC = KD инициирует перпендикулярность! 2. Где бы не находилась точка $M$ при условии равенства отрезков $MC=KD$ всегда получается $S_{AMCK}=\frac{1}{2} S_{ABCD}$. Докажем это. Пусть $BM=x$ . Выразим площади через $x$: $S_{ABM}=\frac{1}{2} x\cdot AB$, $S_{AKD}= \frac{1}{2} (AB-x)\cdot AD$ $S_{AMCK}=AB^2-\frac{1}{2} \cdot AB \cdot (x-(AB-x))=\frac{1}{2} AB^2$. Значит, какой бы не был $x$ площадь четырехугольника равна половине площади квадрата. Факт.
Задача 3: Найти площадь ромба $ABCD$, в котором $\angle C=60^o$ , а меньшая диагональ равна $12$ см.
- Решение: Рассмотрим $\bigtriangleup BCD$. Что в нём равного? $\Rightarrow$ каков данный треугольник?
- По условию, угол $\bigtriangleup BCD$ у вершины $\angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=40$ см.
- Площадь $\bigtriangleup BCD$ найдем по Герону: полупериметр $p=\frac{1}{2}\cdot\left(a+b+c\right)=\frac{1}{2}\cdot\left(12+12+12\right)=18$ , все стороны $=12$
- $S_{BCD}=\sqrt{p\cdot\left(p-a\right)\cdot\left(p-b\right)\cdot\left(p-c\right)}=\sqrt{18\cdot\left(18-12\right)\cdot\left(18-12\right)\cdot\left(18-12\right)}=\sqrt{18\cdot 6 \cdot 6\cdot 6}=35\sqrt{3}$


Задача 4: В ромбе $ABCD$ известны диагонали $AC=2$, $BD=2\sqrt{2}-2$ . Найти высоту и угол ромба.
- Свойство диагоналей в ромбе: они перпендикулярны ... они делятся пополам ... они делят углы пополам:
- $BO=\frac{BD}{2}=\sqrt{2}-1$, $AO=\frac{AC}{2}=1$. $BO\perp AO$ $\to$ $\bigtriangleup ABO$ - прямоугольный:
- Площадь: $S_{ABO}=\frac{1}{2} \cdot AO\cdot BO=\frac{\sqrt{2}-1}{2}$ Сторона ромба: $AB=\sqrt{AO^2+BO^2}=\sqrt{(\sqrt{2}-1)^2+1}=\sqrt{4-2\sqrt{2}}$
- Ромб поделен на 4 равных треугольника $\to$ площадь ромба: $S_{ABCD}=4\cdot S_{ABO}=2(\sqrt{2}-1)$.
- Для ромба $\to$ $S_{ABCD}=AD\cdot BE$, $AD=AB$ $\Rightarrow$ высоту находим через площадь: $BE=\frac{S_{ABCD}}{AB}=\frac{2(\sqrt{2}-1)}{\sqrt{4-2\sqrt{2}}}$
- Упростим радикальное, $\frac{a}{\sqrt{b}}=\frac{a}{b} \cdot \sqrt{b}$: $BE=\frac{2(\sqrt{2}-1)}{4-2\sqrt{2}}\cdot \sqrt{4-2\sqrt{2}}=\frac{2(\sqrt{2}-1)}{2\sqrt{2}(\sqrt{2}-1)}\cdot \sqrt{4-2\sqrt{2}}=\frac{\sqrt{4-2\sqrt{2}}}{\sqrt{2}}$
- Во сколько раз в $\bigtriangleup ABE$ гипотенуза больше катета : $\frac{AB}{BE}=\frac{\sqrt{4-2\sqrt{2}}}{\frac{\sqrt{4-2\sqrt{2}}}{\sqrt{2}}}=\sqrt{2}$ - раза.
- В прямоугольном треугольнике отношение $\sqrt{2}$ - раза означает, что угол $45^o$ $\Rightarrow$ угол ромба $\angle BAD=45^o$
![]()
Решите устно:

Упражнения (A):
Упражнения (В):
Упражнения (С):
Задачи из сайта https://resh.edu.ru :
75 ∠°ADC AB ⊥ BD ∠BCD = 30°
Задачи (coded): 1) В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO. 2) В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC. 3) Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба. 4) Высота ромба равна 7 см, острый угол равнее 30°. Найдите площадь ромба. 5) Диагонали ромба равны 24 см и 36 см. Найдите площадь ромба. Одна из диагоналей ромба равна 48, а его сторона равна 25. Найдите площадь ромба. 6) Одна из диагоналей ромба равна 48, а его сторона равна 25. Найдите площадь ромба. 7) Все стороны параллелограмма равны, а его периметр равен 64 см. Один из углов, который диагональ образует со стороной, равен 75°. Найдите площадь параллелограмма. 8) Дан ромб ABCD. Высота BH делит сторону AD пополам. Найдите ∠ADC. 9) Дан ромб ABCD. Биссектриса СК угла ВСА перпендикулярна стороне АВ. Найдите ∠ADC. 9) Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Квадрат:
Дан квадрат ABCD. На стороне АD построен равносторонний треугольник АDO так, что вершина О находится внутри квадрата. Найдите ∠BOC. Дан квадрат ABCD, О – точка пересечения диагоналей. Точка М принадлежит стороне ВС. Прямая МО пересекает сторону AD в точке К. Известно, что ∠OKD=72∘. Найдите ∠AOM. Дан квадрат ABCD. На продолжении стороны AD за точку D отмечена точка М так, что DM = DB. Найдите ∠DMB. На сторонах ВС и CD квадрата ABCD отмечены точки М и К соответственно, MC = KD. Отрезки DM и AK пересекаются в точке О, 2 ОМ = АМ. Найдите угол АМО. На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 7. Дан квадрат ABCD. На стороне АD построен равносторонний треугольник АDO так, что вершина О находится внутри квадрата. Найдите ∠BOC.
Задача 8. Дан квадрат ABCD, О – точка пересечения диагоналей. Точка М принадлежит стороне ВС. Прямая МО пересекает сторону AD в точке К. Известно, что ∠OKD=72∘. Найдите ∠AOM.
Задача 9. Дан квадрат ABCD. На продолжении стороны AD за точку D отмечена точка М так, что DM = DB. Найдите ∠DMB.
Задача 26. На сторонах ВС и CD квадрата ABCD отмечены точки М и К соответственно, MC = KD. Отрезки DM и AK пересекаются в точке О, 2 ОМ = АМ. Найдите угол АМО.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
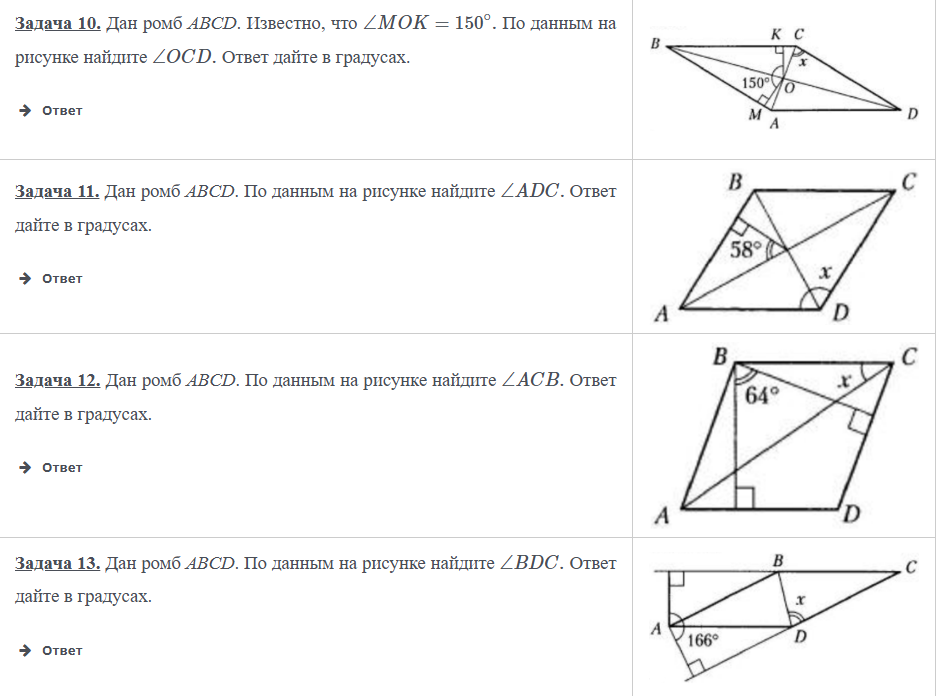
Ромб: задачи 10-11-12-13 через рисунок