Стандартное обозначение прямоугольного треугольника $\bigtriangleup ABC$ :
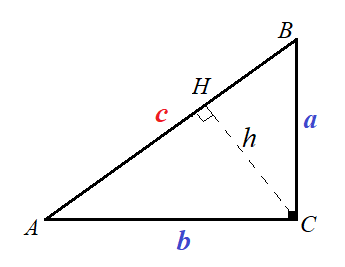
катеты $a = BC$
$b = AC$
высота $h=CH$
прямой $\angle C$ = $90^o$
острый $\angle A$ = $\angle BAC$
острый $\angle B$ = $\angle ABC$
Теорема Пифагора Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов $AB^2=AC^2+BC^2$.
Площадь прямоугольного треугольника $S_{ABC}=\frac{a\cdot b}{2}$ . Площадь = катет * катет : 2 .
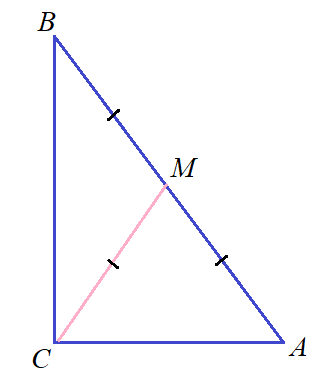
Напротив 30 градусов лежит катет, равный половине гипотенузы прямоугольного треугольника .
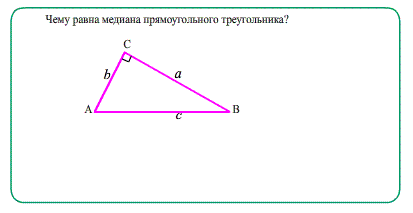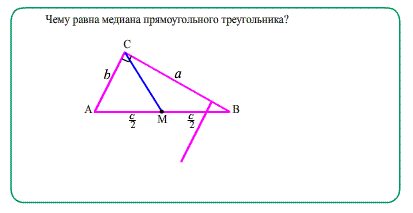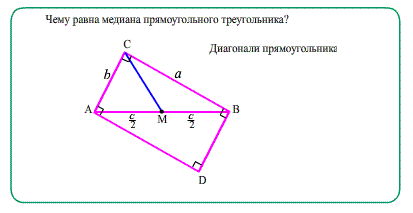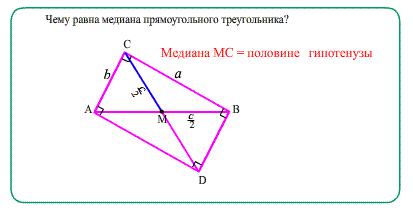
Медиана, опущенная на гипотенузу в прямоугольном треугольнике, равна половине гипотенузы.
Высота прямоугольного треугольника делит его на два подобных между собой и исходному треугольнику.
Высота прямоугольного треугольника равна средне-геометрическому частей гипотенузы, на которые делит гипотенузу.
Подобные прямоугольные треугольники имеют хотя бы по одному равные острые углы. Признак I:
Тригонометрия углов в прямоугольном треугольнике, функции углов:
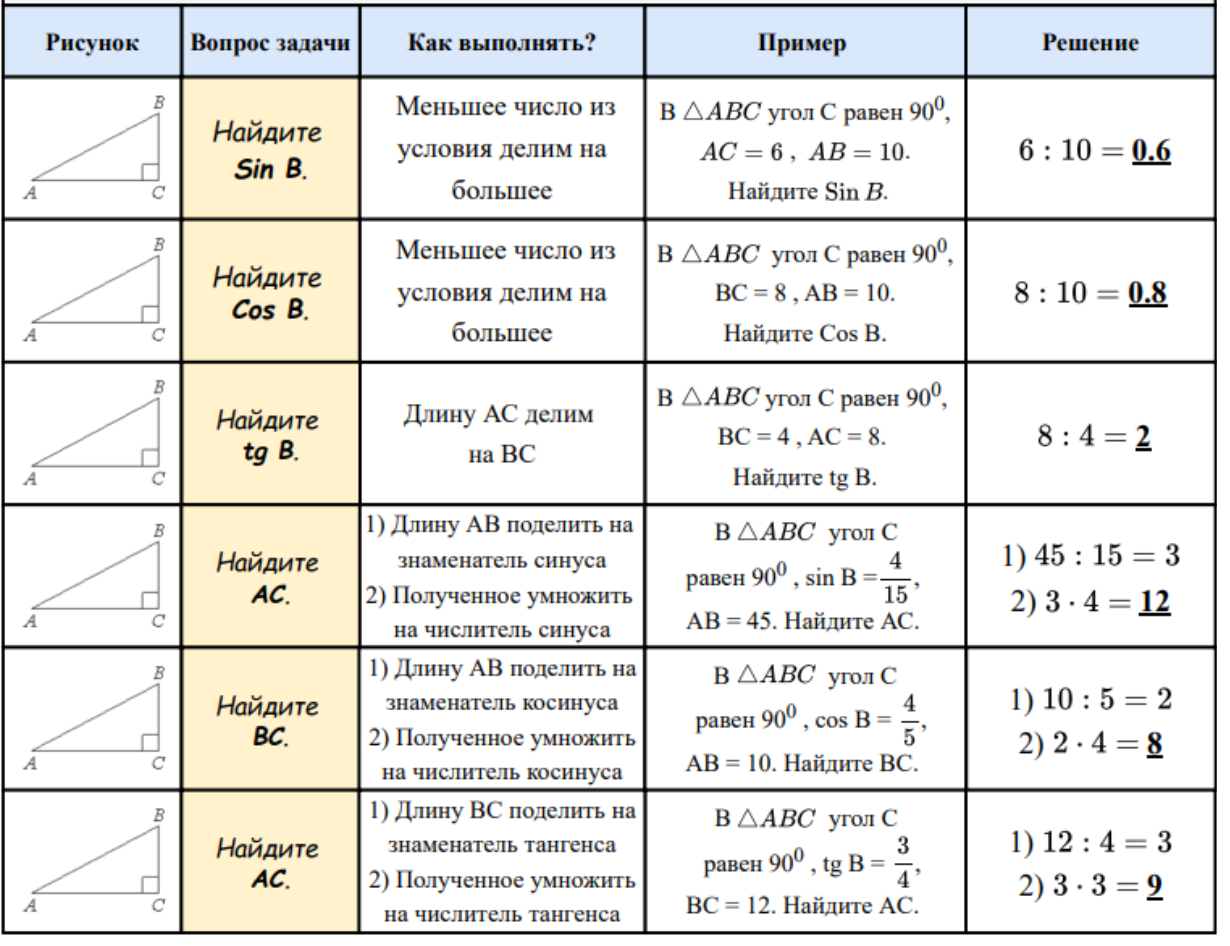
- синусом угла называется отношение противолежащего катета к гипотенузе, $\sin\alpha=\frac{a}{c}$
- косинусом угла называется отношение прилежащего катета к гипотенузе, $\cos\alpha=\frac{b}{c}$
- тангенсом угла называется отношение противолежащего катета к прилежащему, $\tg\alpha=\frac{a}{b}$
- котангенсом угла называется отношение прилежащего катета к противолежащему, $\ctg\alpha=\frac{b}{a}$
Замечание: Отношения сторон не зависят от длин катетов и гипотенузы, они зависят только от углов. Угол здесь очень важен. Не важно какие стороны в треугольнике длинные или короткие , важно их отношение - оно всегда одно и то же.
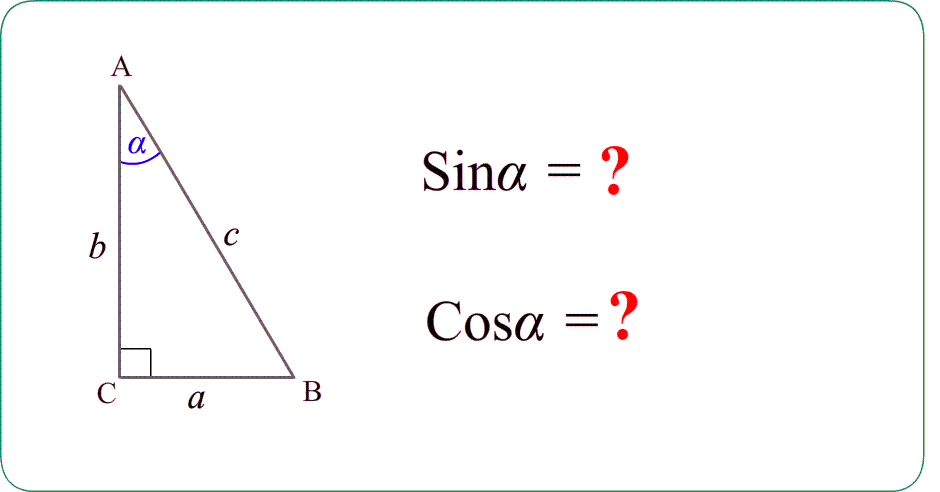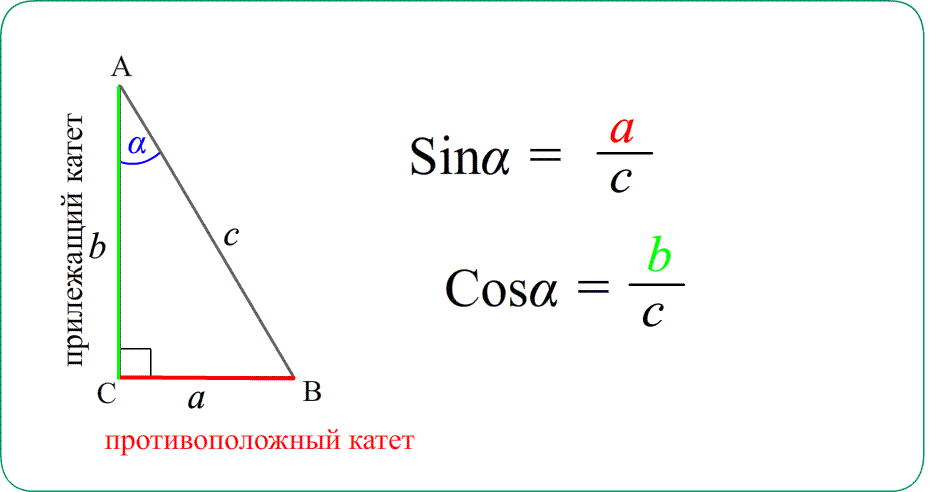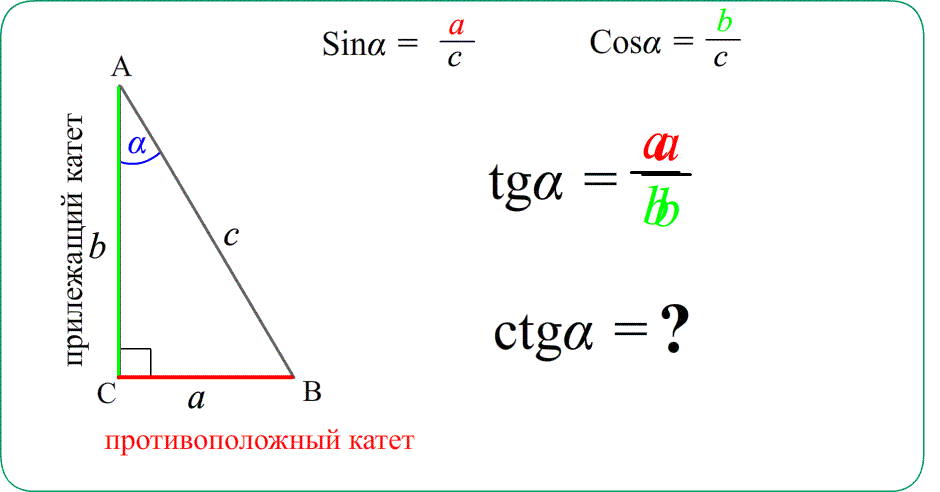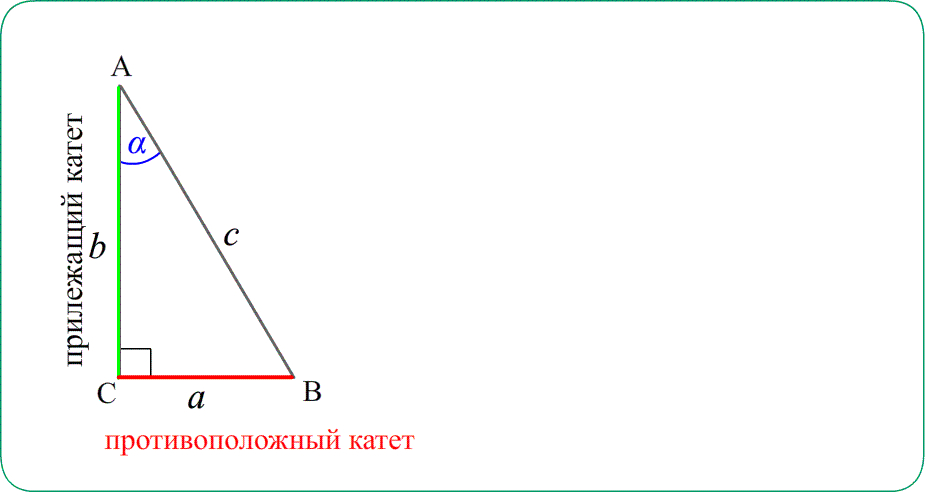
Формулы, соотношений в прямоугольном треугольнике, определения тригонометрических функций острых углов:
Заие. $\sin A=\frac{BC}{AB}$ $\cos A=\frac{AC}{AB}$ $\tg A=\frac{BC}{AC}$ $\ctg A=\frac{AC}{BC}$
Заие. $\sin B=\frac{AC}{AB}$ $\cos B=\frac{BC}{AB}$ $HC=AC\cdot\sin A$ $\frac{HC}{BC}=\frac{AC}{AB}$ $\angle ACH=\angle B$
Заче. $S=\frac{a\cdot b}{2}$ $S=\frac{AB\cdot CH}{2}$ $HC=BC\cdot\sin B$ $\frac{HC}{AC}=\frac{BC}{AB}$ $\angle BCH=\angle A$
Замечание: Катеты можно выразить через гипотенузу и синус (или косинус) острого угла и наоборот.
- Если в прямоугольном треугольнике известны две величины : две стороны или сторона и тригонометрия угла ...
- ... все остальное можно вычислить - найти - расчитать по формулам.
- Тождества: $\sin^2\alpha+\cos^2\alpha=1$ ; $\tg\alpha=\frac{\sin\alpha}{\cos\alpha}$ ; $\ctg\alpha=\frac{1}{\tg\alpha}=\frac{\cos\alpha}{\sin\alpha}$ .
- Связанность: Cинус, косинус, тангенс и котангенс одного угла связаны между собой основными тригонометрическими тождествами. Знаем одну функцию - значит можем (при наличии необходимой дополнительной информации) вычислить и все остальные.
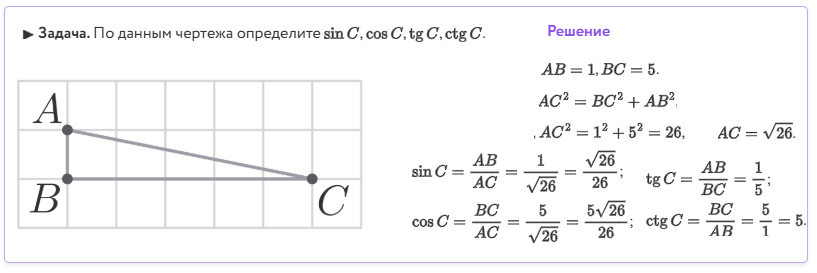
Задача 1: На клетчатой бумаге с размером клетки 1см х 1см изображен треугольник.
__ 
Задача 2: В треугольнике $\bigtriangleup ABC$ дана высота $BH=7$ и угол у основания $\angle BCA=60^o$, а косинус другого угла $\cos \angle BAC=\frac{2\sqrt{2}}{3}$: . Найти стороны треугольника.
- Высота поделила наш треугольник на два прямоугольных треугольника $ABH$, $CBH$
- В треугольнике $ABH$ известны катет и косинус угла. Найдем все стороны. Сперва по косинусу найдем синус, тангенс:
- $\sin \angle BAC=\sqrt{1-(\cos \angle BAC)^2}=\sqrt{1-(\frac{2\sqrt{2}}{3})^2}=\sqrt{1-\frac{4\cdot 2}{9}}=\frac{1}{3}$ теперь, $\tg \angle BAC=\frac{\sin \angle BAC}{\cos \angle BAC}=\frac{\frac{1}{3}}{\frac{2\sqrt{2}}{3}}=\frac{1}{2\sqrt{2}}$
- Из определения синуса $\sin BAH=\frac{BH}{AB}$ выразим гипотенузу $AB=\frac{BH}{\sin BAH}$ , найдем $AB=\frac{7}{\frac{1}{3}}=21$
- Из $\tg \angle BAC=\frac{BH}{AH}$ $\Rightarrow$ выразим катет $AH=\frac{BH}{\tg \angle BAC}$ $\Rightarrow$ $AH=\frac{7}{\frac{1}{2\sqrt{2}}}=14\sqrt{2}$
- В прямоуголльном треугольнике $CBH$ известен катет и хороший угол $60^o$. Рассчитаем другой катет и гипотенузу.
- Из $\sin 60^o=\frac{BH}{BC}$ подставляя значения $\frac{\sqrt{3}}{2}=\frac{7}{BC}$ получим, $BC= \frac{7\cdot 2}{\sqrt{3}}= \frac{14\sqrt{3}}{3}$
- Из $\tg 60^o=\frac{BH}{CH}$ $\Rightarrow$ $\sqrt{3}=\frac{7}{CH}$ $\Rightarrow$ $CH= \frac{7}{\sqrt{3}}= \frac{7\sqrt{3}}{3}$
- Сторону $AC$ найдем как сложение двух частей $AC=AH+HC=14\sqrt{2}+\frac{7\sqrt{3}}{3}=7\cdot +\frac{6\sqrt{2}+\sqrt{3}}{3}$
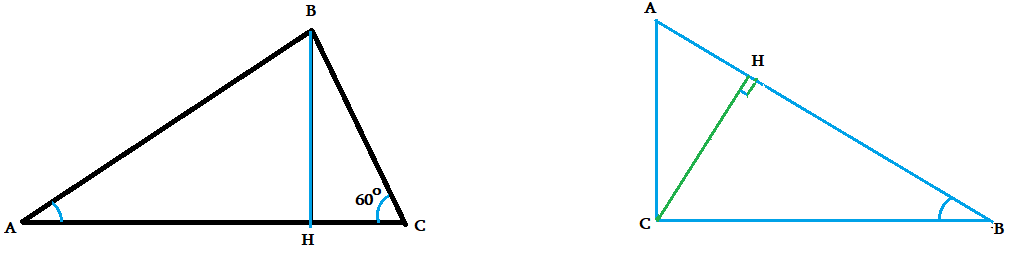
Задача 3: В прямоугольном треугольнике $\bigtriangleup ABC$ дана высота $CH=12$ прямого угла и тангенс одного из острых углов, $\tg \angle CBA=\frac{\sqrt{6}}{4}$ . Найти отрезки, на которые высота делит гипотенузу
- Высота $CH$ делить треугольник на два прямоугольных треугольника $ACH$, $BCH$. С теми же углами, как у $\bigtriangleup ABC$.
- В прямоугольном $\bigtriangleup AHC$ по катету и тангенсу найдем другой катет: $\tg \angle BAC=\frac{CH}{AH}$ $\Rightarrow$ $AH=\frac{CH}{\tg \angle BAC}=\frac{12}{\frac{\sqrt{6}}{4}}=8\sqrt{6}$
- Тангенс другого острого угла $ \angle ABC$ равен котангенсу $\angle BAC$: $\tg \angle ABC=\ctg \angle BAC=\frac{1}{\tg \angle BAC}=\frac{4}{\sqrt{6}}$
- В прямоугольном $\bigtriangleup BHC$: $\tg \angle HBC=\frac{CH}{BH}$ выразим катет $\Rightarrow$ $BH=\frac{CH}{\tg \angle HBC}=\frac{12}{\frac{4}{\sqrt{6}}}=3\sqrt{6}$
- Произведение отрезков гипотенузы $AH\cdot BH=8\sqrt{6}\cdot 3\sqrt{6}=24\cdot 6=144$, Квадрат высоты $CH^2=12^2=144$.
- Теорема: Квадрат высоты равен произведению отрезков гипотенузы. $AH\cdot BH=\frac{CH}{\tg \angle BAC}\cdot \frac{CH}{\ctg \angle BAC}=CH^2$
Задача 4: В прямоугольном треугольнике известны площадь $S=120m^2$ и синус угла $\frac{5}{13}$ .
Задача 2: Найти высоту, опущенную на гипотенузу.
- Решение: Пусть треугольник АВС с прямым углом $C=90^o$, катетами $a$ и $b$ ; $\sin A=\frac{5}{13}$ ,
- Выразим катеты через гипотенузу и угол $A$ : $a=c\cdot\sin A$ $b=c\cdot\cos A$. Подставим в формулу площади через
- катеты $S=\frac{ab}{2}=\frac{c^2\cdot\sin A\cdot\cos A}{2}$. Отсюда выразим гипотенузу $c^2=\frac{2S}{\sin A\cdot\cos A}$.
- Вычислим косинус угла $A$ при известном для него синусе $A$ : $\cos A=\sqrt{1-\sin^2A}=\sqrt{1-\frac{25}{13}}=\frac{12}{13}$
- Найдем гипотенузу $c^2=\frac{2S}{\sin A\cdot\cos A}$ , $c^2=\frac{2\cdot120\cdot m^2}{\frac{5}{12}\cdot\frac{12}{13}}=4\cdot13^2\cdot m^2$ , $c=26m$
- Другая формула той же площади $S=\frac{1}{2}\cdot c\cdot h$ позволит выразить высоту через площадь и гипотенузу, на которую эта
- высота опущена: $h=\frac{2\cdot S}{c}=\frac{2\cdot120\cdot m^2}{26\cdot m}=\frac{120}{13}m$ . Ответ: $h=\frac{120}{13}m$ .
Формулы и свойства прямоугольного треугольника
Рассуждения о прямоугольном треугольнике:
Если к прямоугольному треугольнику приложить точно такой же, можно получить прямоугольник. Как бы два треугольника превратили в "половинки" прямоугольника , гипотенузой стала диагональ прямоугольника.
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы. Середина гипотенузы находится на одинаковом расстоянии от всех трех вершин прямоугольного треугольника , т.к. эта точка есть точка пересечения диагоналей прямоугольника, получаемого достроением прямоугольного треугольника до "обрамляющего" прямоугольника.
Высота прямоугольного треугольника, проведенная к гипотенузе, "режет" треугольник на ему же подобные копии, потому что у всех трех треугольников углы в точности одинаковые .

Факты: что надо видеть и знать при прямоугольных треугольниках
- 1. Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту .
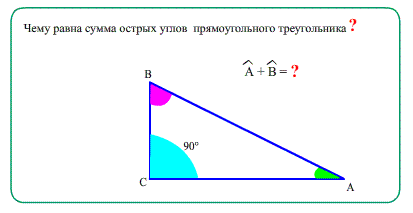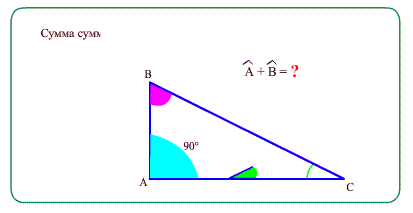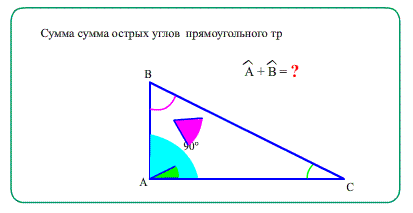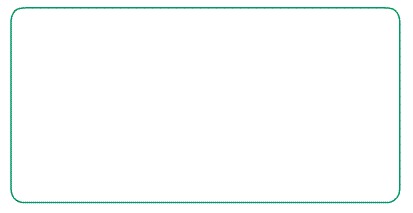
- 2. "О сумме острых углов": в прямоугольном треугольнике сумма острых углов равна 90 градусов.
- 3. "О $30^o$": в прямоугольном с углом $30^o$ катет напротив этого угла равен половине гипотенузы. Если к такому треугольнику
про приложить точно такой же получится равностронный с углами $60^o$ и катет напротив $30^o$ окажется ровно половиной
про стороны равностороннего ,а значит это катет $a=\frac{c}{2}$ ; другой катет легко получить по теореме Пифагора : $b=\frac{\sqrt{3}}{2}c$ . - 4. "О $45^o$": прямоугольный $\bigtriangleup$ с острым углом в $45^o$ является равнобедренным ; его гипотенуза $c=\sqrt{2}$ * катет.
- 5. "О равнобедренном прямоугольном треугольнике": углы при основании равны и их сумма равна $90^o$ $\Rightarrow$ оба угла по $45^o$; катеты равны и по т. Пифагора $a^2+a^2=c^2$ $\Rightarrow$ оба катета $a=b=\frac{\sqrt{2}}{2}c$ и $c=\sqrt{2}a$ .
- 6. "О высоте в прямоугольном": $h$ проведенная из угла $90^o$ делит исходный треугольник на два ему подобных.
про Ведь высота поделила треугольник на два прямоугольных треугольника , причем с одинаковыми острыми углами ,
про потому что , если одни из острых углов треугольников совпадают, а их сумма двух $90^o$ , то и другие совпадут $\Rightarrow$
про все эти треугольники подобные между собой и исходному. - 7. "Еще о высоте " : высота равна среднегеометрическому отрезков, на которые она делит гипотенузу:
про $CH=h=\sqrt{AH\cdot BH}$ , $h\cdot c=a\cdot b$ . - 8. "О медиане, проведенной к гипотенузе" : она равна половине гипотенузы $CM=\frac{AB}{2}$ , а так же радиусу описанной окружности $CM=R$. Точка $M$ на гипотенузе равноудалена от всех трех вершин.

Тригонометрия хороших углов: 30 , 45, 60, 120, 135, 150
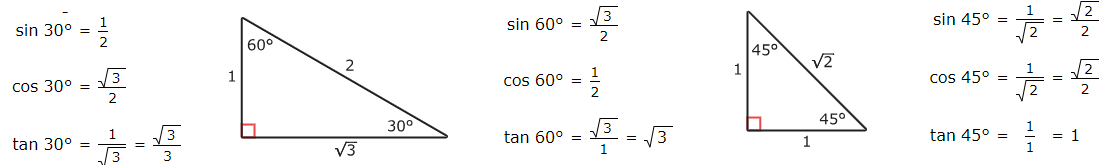
- Формула приведения тупых углов $90 < \alpha < 180$ к смежным острым $180-\alpha$: синус тупого угла такой же, как у своего смежного. косинус, тангенс, котангенс тупого такой же, как минус своего смежного:
- $\sin\left(\alpha\right)=\sin\left(180-\alpha\right)$ $\cos\left(\alpha\right)=-\cos\left(180-\alpha\right)$ ,
- $\tg\left(\alpha\right)=-\tg\left(180-\alpha\right)$ $\ctg\left(\alpha\right)=-\ctg\left(180-\alpha\right)$
Решаем устно:

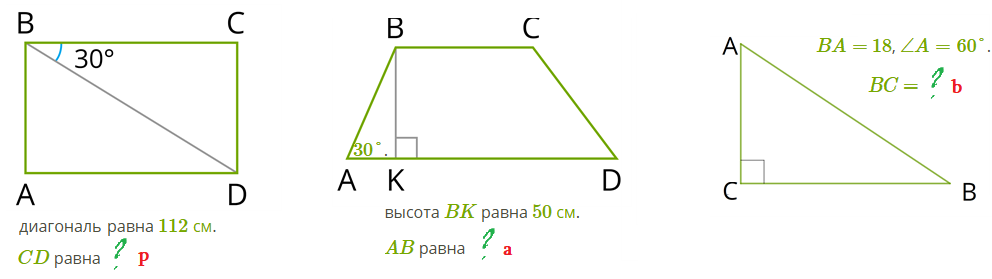
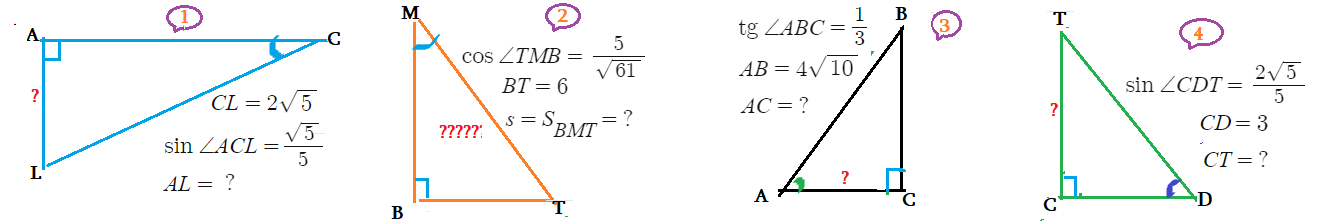

Упражнения (A):
Упражнения (B):
еще задачи: