Подобие треугольников

Примеры подобий:

1. Предмет и его фотография. Если предмет в   5 раз больше фотографии, то каждая сторона предмета будет ровно в 5 раз длиннее такой же стороны на фотографии. При этом углы останутся неизменныими - это самое важное при подобиях;

2. Zoom фотоаппарата или бинокль передает смысл коэффициента подобия;

3. Копирование:    Увеличить или уменьшить, сделать копии чего либо - получатся подобные фигуры.

Три признака подобия двух треугольников

Теорема     О трех признаках подобия двух треугольников. Два треугольника подобны, если:

Признак I.   Равенство двух углов.

• Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
• $\angle A=\angle A_1$ , $\angle B=\angle B_1$ $\Rightarrow$ $\bigtriangleup ABC\sim \bigtriangleup A_1B_1C_1$

Признак II.   Пропорциональность двух сторон и равенство угла между ними".

• Если две стороны одного треугольника пропорциональны соответственно двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны:
  
• $\angle A=\angle A_1$ ,   $\frac{AC}{A_1C_1}=\frac{AB}{A_1B_1}$   $\Rightarrow$ $\bigtriangleup ABC\sim \bigtriangleup A_1B_1C_1$

Признак III.   Пропорциональность трёх сторон.

• Если три стороны одного треугольника пропорциональны соответственно трем сторонам второго треугольника, то такие треугольники подобны:
• $\frac{AC}{A_1C_1}=\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}$    $\Rightarrow$ $\bigtriangleup ABC\sim \bigtriangleup A_1B_1C_1$

                   

Коэффициентом       подобия треугольников называется отношение соответственных сторон        $k=\frac{AC}{A_1C_1}$

• Отношение всех соответствующих отрезков     $k=\frac{a}{a_1}=\frac{b}{b_1}=\frac{c}{c_1}=\frac{h_c}{h_{c1}}=\frac{m_b}{m_{b1}}=\frac{b_a}{b_{a1}}$ .
• Коэффициент подобия равен отношению соответственных сторон первого и второго треугольников.
  
• Квадрат   коэффициента подобия говорит об отношении площадей      $k^2=\frac{S}{S_1}$.

Соответственные (сходственные) стороны - те, которые являются копиями друг друга в подобных фигурах. У подобных фигур одинаковый состав углов. Увидеть подобие означает найти - для каждого угла из первой фигуры найдется равный ему угол из второй фигуры. Напротив таких равных углов находятся сходственные стороны.

• Как меняются длины (отрезки, дуги) при подобии?   Увеличиваются в   $k$ - раз. Одномерные -   $D^1$ - размерность ;

• Как соотносятся площади при подобии?    Увеличиваются в    $k^2$ - раз. Двумерные - $D^2$ ;

• Каково отношение объемов при подобии?    Увеличиваются в    $k^3$ - раз. Трехмерные - $D^3$ - размерность ;

• Что не меняется при подобии?     Угол.    $k^0$ - раз.    0 - мерные - $D^0$ .   Угол = дуга/радиус.

Теорема     О трех признаках подобия двух прямоугольных треугольников.

• Признак I:     если хотя бы один острый угол первого треугольника равен какому - либо острому углу другого;
  
• Признак II:    если катеты одного пропорциональны катетам другого;
  
• признак III:   если гипотенуза и катет одного пропорциональны гипотенузе и катету другого.
  

Теорема     В треугольнике параллельная стороне линия отсекает подобный ему треугольник.

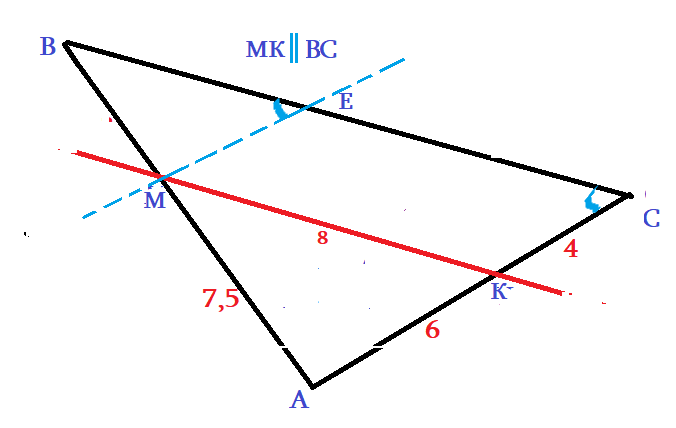
Задача 1:      Линия $MK$ параллельна стороне $BC$. Известно: отрезки $AK=6$, $AM=7,5$, $KC=4$, $MK=8$. Вычислить отношения сторон треугольников АМК и АВС. Доказать подобие треугольников.

• $MK\parallel BC$        по Фалесу:           $\frac{AM}{AK}=\frac{MB}{KC}$         подставляя значения, получим     $BM=5$.     Тогда       $AB=12,5$.
• Дополнительное построение:        проведем к $AC$    параллельную      $МЕ$.          Очевидно:       $EC=8$,      $ME=4$.
• $AC\parallel МЕ$,        еще раз Фалес:         $\frac{AM}{EC}=\frac{MB}{BE}$             $\Rightarrow$            $BE=\frac{16}{3}$,         сторона    $BC=BE+EC=\frac{40}{3}$
• Находим пропорции:         $\frac{AK}{AC}=\frac{6}{10}=\frac{AM}{AB}=\frac{7,5}{12,5}=\frac{MK}{BC}=\frac{8}{\frac{40}{3}}=0,6$ -   коэффициент подобия        $\bigtriangleup AMK \sim \bigtriangleup ABC$

                              

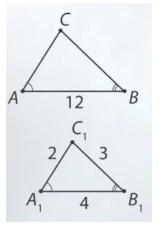
Задача 2:       Дано:        $\bigtriangleup ABC$ ; $\bigtriangleup A_1B_1C_1$    $\angle A=\angle A_1$ ; $B=\angle B_1$ ; $A_1B_1=4$ $B_1C_1=3$ $C_1A_1=2$ $AB=12$        Найти:       $BC$ и $CA$

• Решение: Два угла в одном равны двум углам в другом.... По 1-му признаку подобия: $\bigtriangleup ABC\sim \bigtriangleup A_1B_1C_1$
• Определим коэффициент подобия данных:    $k=\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1}$               Следовательно,
  
• $\frac{CA}{2}=3$          $CA=2\cdot 3=6$           $\frac{BC}{3}=3$         $BC=3\cdot 3=9$ .            Ответ: $CA=6$ $BC=9$

Очевидно Подобные:      Треугольник со сторонами 6, 9, 12 подобен треугольнику со сторонами 2, 3, 4 - каждая сторона первого треугольника ровно в три раза больше "своей сходственной" стороне другого треугольника. Коэффициент подобия = 3.

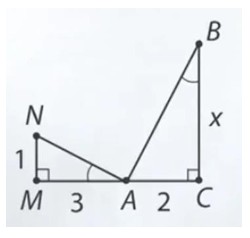
Задача 3:   Дано:     $\bigtriangleup ABC$ и $\bigtriangleup NAM$   прямоугольные $AM=3$   $AC=2$    $\angle A=\angle B$      Найти:    $x=BC$

• Решение:   в каждом треугольнике есть прямой угол и $\angle A=\angle B$ (1-ый признак подобия треугольников): $\bigtriangleup ABC\sim \bigtriangleup NAM$.
• Так как треугольники подобные, то отношения сходственных сторон у них равны. Какие схожие?
• Для определения сходственных сторон необходимо помнить, что они лежат напротив равных углов: $AC$ и $NM$,     $AB$ и $NA$,     $BC$ и $AM$.
• $\frac{AC}{NM}=\frac{AB}{NA}=\frac{BC}{AM}$             отдельно выпишем равенство:        $\frac{AC}{NM}=\frac{BC}{AM}$
• Подставим известные значения:    $\frac{2}{1}=\frac{x}{3}$        $1\cdot x=2\cdot 3$       $x=6$        Ответ:   $x=6$

Задача 4:        Стороны треугольника 15 см, 20 см и 30 см. Найдите стороны подобного треугольника с периметром 26 см.

• Решение: Отношение периметров подобных треугольников равно коэффициенту подобия.
• Периметр    $\bigtriangleup A_1B_1C_1$   нам задан,   периметр    $\bigtriangleup ABC$ мы сможем найти, т.к. заданы длины его сторон.
• Таким образом мы найдем коэффициент подобия и определим искомые длины сторон:
• $P_{\bigtriangleup ABC}=15см+20см+30см=65см$   .   Коэффициент:       $k=\frac{P_{\bigtriangleup A_1B_1C_1}}{P_{\bigtriangleup ABC}}=\frac{26}{65}$   
  
• $\Rightarrow$       $a_1=ka=\frac{26\cdot 15}{65}=6$см    ,    $b1=kb=\frac{26\cdot 20}{65}=8$см      ,     $c1=kc=\frac{26\cdot 30}{65}=12см$ .

               

Задача 5:            На одной стороне угла $\angle A$   отложены отрезки $AB=6$ и $AC=20$. На другой стороне $AD=8$ $AE=15$ . Подобны ли треугольники   $ACD$ и $AEB$ ?

• Решение:      У обоих треугольников    $\bigtriangleup ACD$   и $\bigtriangleup AEB$   есть равный угол     $\angle A$, общий угол для обоих.
• Две стороны ( $AD$ и $AC$ ) треугольника   $\bigtriangleup ACD$     пропорциональны двум сторонам   ($AB$ и   $AE$)   треугольника $\bigtriangleup AEB$ !
  
• почему?   Проверим "на числах", выполняется ли    пропорция, равны ли отношения сторон:       $\frac{AD}{AC}$       ?=?      $\frac{AB}{AE}$
• Отношение     $\frac{AD}{AC}=\frac{8}{20}=\frac{2}{5}$ .       Отношение   $\frac{AB}{AE}=\frac{6}{15}=\frac{2}{5}$.         Видно, что эти отношения равны.
• Итак: 2 стороны одного пропорциональны двум другого!           Кроме того,    $\angle A$   является общим для двух треугольников.
• По второму признаку подобия       $\Rightarrow$          $\bigtriangleup ACD\sim \bigtriangleup AEB$

Задача 6:        В равнобедренном треугольнике $\bigtriangleup ABC$ с углом $\angle A=36^o$ из вершины $B$ основания проведена биссектриса $BL$. Доказать подобие треугольников $\bigtriangleup ABC$ и $\bigtriangleup BLC$.

• Дано:                $\bigtriangleup ABC$ равнобедренный;   $AB=AC$    $\angle A=36^o$ $\angle LBA=\angle LBC$ ( $BL$ - биссектриса).
• Доказать:      $\bigtriangleup ABC\sim \bigtriangleup BLC$.
• Доказательство: Так как в равнобедренном треугольнике задан угол при вершине, то можно найти углы при основании:
• $\angle B+\angle C=2\cdot \angle B=180^0-\angle A=180^0-36^0=144^0$
• $BL$ - биссектриса       $\Rightarrow$ $\angle LBA=\angle LBC=\frac{\angle B}{2}=\frac{72^o}{2}=36^o$.
• B     $\bigtriangleup BLC$ :   $\angle BLC=180^o-\angle C-\angle LBC=180^o-72^o-36^o-72^o$.        Таким образом, ....
  
• $\bigtriangleup ABC$ и $\bigtriangleup BLC$    - это   равнобедренные с равными углами при вершине     $\angle A=\angle LBC=36^o$.
  
• Равнобедренные треугольники с равными углами при вершине подобны, (состав углов одинаковый?):         $\bigtriangleup ABC\sim \bigtriangleup BLC$.     Что и требовалось доказать.

                           

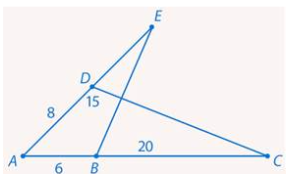
Задача 7:       На одной стороне угла отложены отрезки   $AB=6$    и   $AC=20$. На другой стороне    $AD=8$ и   $AE=15$. Подобны ли треугольники   $\bigtriangleup ACD$ и   $\bigtriangleup AEB$ ?

• Надо изучить отношения сторон этих треугольников и   обнаружить равные пропорции,
• Отношения   $\frac{AB}{AE}=\frac{6}{15}=\frac{2}{5}$    и    $\frac{AD}{AC}=\frac{8}{20}=\frac{2}{5}$   одинаковые, пропорциональность сторон выполняется.
• Т.к.    $\frac{AB}{AE}=\frac{AD}{AC}$   и    $\angle EAB=\angle CAD$ ,    по 2-му признаку подобия:        $\Rightarrow$       есть подобие        $\bigtriangleup ACD \sim \bigtriangleup AEB$

Следствия подобия,   Факты

Средняя линия треугольника параллельна стороне и равна половине этой стороны.

Медианы треугольника пересекаются в одной точке и делятся этой точкой в пропорции 2 : 1 .

Высота прямоугольного треугольника делит его на два подобных между собой и исходному треугольнику.

Высота прямоугольного треугольника равна средне-геометрическому частей гипотенузы, на которые делит гипотенузу.

Биссектриса угла делит сторону треугольника на два отрезка, пропорциональных двум другим сторонам треугольника..

1. Все прямоугольные треугольники с углом 57 градусов подобны друг другу;

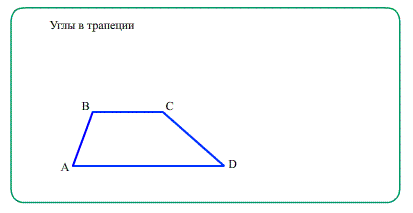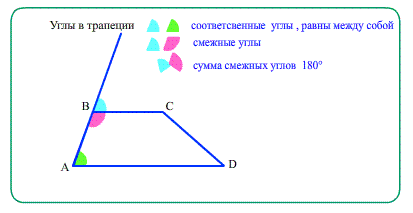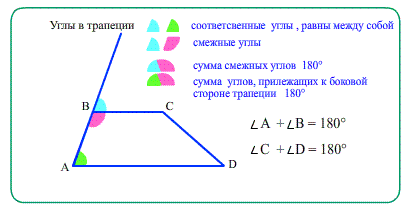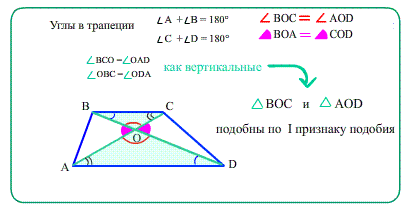
2. Диагонали трапеции при пересечении образуют два подобных друг другу треугольника, прилежащих к основаниям;

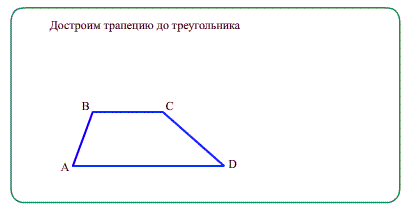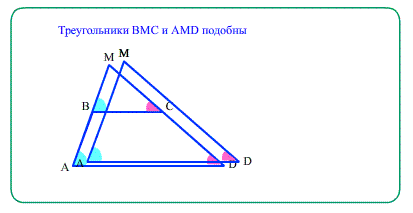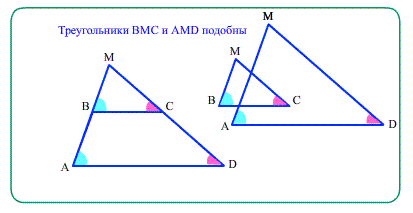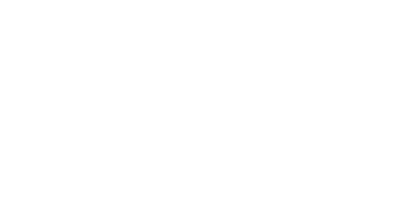
3. При продолжении боковых сторон трапеции до пересечения образуются два подобных треугольника;

4. Если коэффициент подобия к = 3, то каждая сторона первого треугольника в 3 раза больше соответствующей стороне второго треугольника, каждая высота в первом треугольнике в 3 раза больше соответствующей (подобной) высоте во втором, аналогично медианы, биссектрисы в 3 раза больше своих визави. Площадь первого треугольника в 9 раз больше площади другого треугольника. Но углы у обоих треугольников соответственно равны;

5. Угол - 0 мерная величина. Длина отрезка - одномерная величина. Площадь - двухмерная величина. Объем - трехмерная величина.    

Замечание, о главном в подобиях:

• О самом важном при подобии треугольников: какие составы углов? равные? какие стороны соответственные, схожие?
• Соответственные стороны (иногда говорят сходственные ) - это стороны, которые в пропорциях делятся друг на друга.
• Пропорция: сторона a одного треугольника, деленная на соотвественную (сходственную) a сторону второго треугольника.

Три признака равенства треугольников

Если треугольники подобны и коэффициент подобия = 1, то эти треугольники равны. У равных треугольников все части равны.

Теорема о трех признаках равенства двух треугольников    два треугольника равны (совпадают), если:

Признак I:    если две стороны и угол между ними первого треугольника равны соответственно двум сторонам и углу между ними второго;

Признак II:   если сторона и два прилежащих к ней угла первого равны соответственно стороне и двум прилежащим к ней углам второго.

Признак III:    если три стороны одного треугольника равны соответственно трем сторонам второго треугольника.

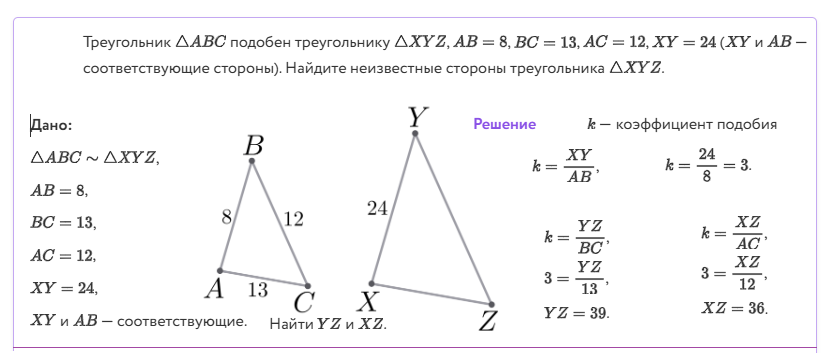
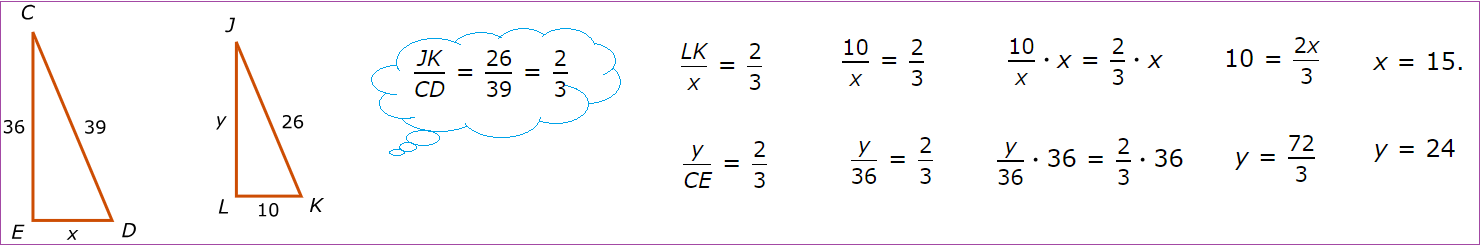
Решите устно:

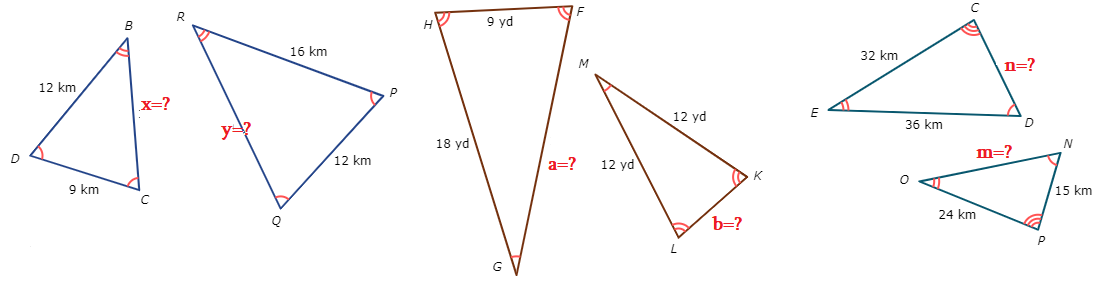
Упражнения (А):

Упражнения (В):

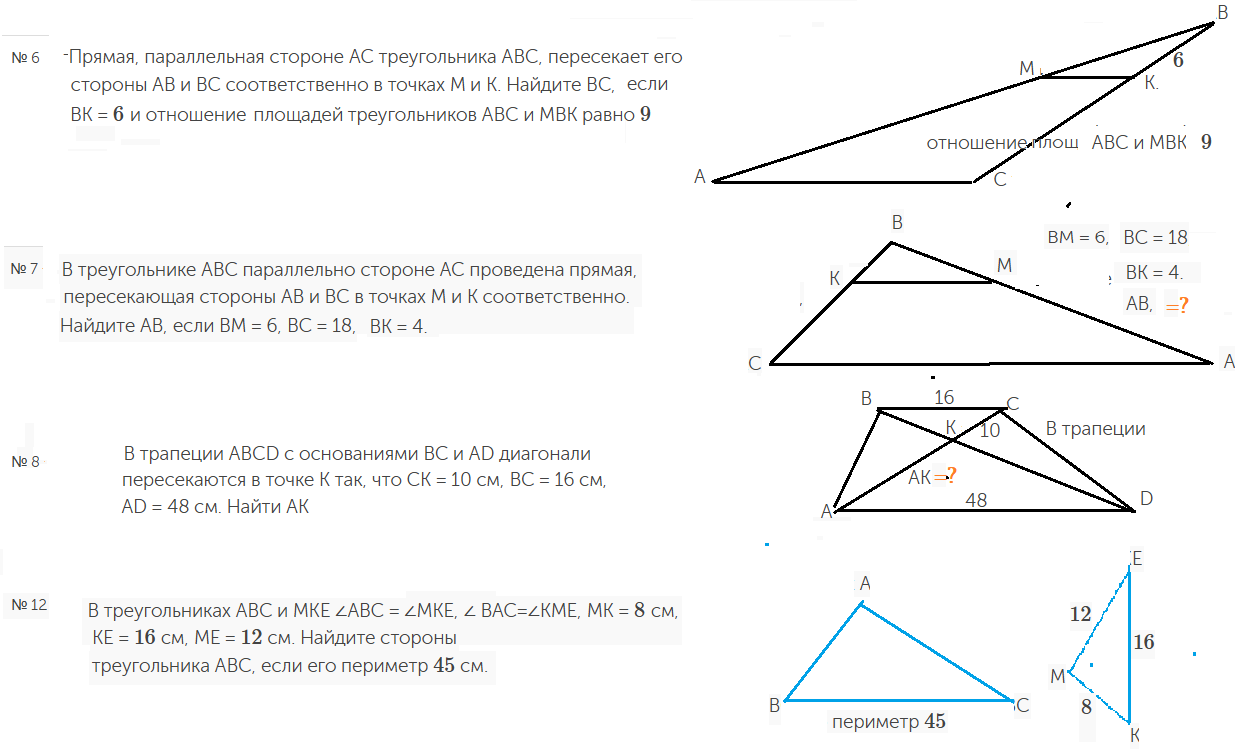
Задачи из сайта https://resh.edu.ru :

Задача 21: Стороны треугольника, образованного средними линиями треугольника ABC, равны 12, 13, 14. Найдите периметр треугольника АВС.

ХХХ Задача 22: Отрезки AB и CD пересекаются в точке E так, что ∠CAE = ∠DBE, AE = 16, BE = 4, ED = 15. Найдите CE.

ХХХ Задача 23: Высота прямоугольного треугольника, проведенная из вершины прямого угла, равна 24 см и делит гипотенузу на отрезки, один из которых равен 36 см. Найдите гипотенузу.

ХХХ Задача 24: Основания трапеции ABCD раны 24 см и 36 см. Диагонали AC и BD пересекаются в точке O. Найдите AO, если OC =8 см.

Задача 25: Прямая, параллельная стороне AC треугольника ABC, пересекает его стороны AB и BC соответственно в точках M и N. Найдите отношение площадей треугольников ABC и MBN, если AB = 18, MB = 12

Задача 26: Прямая, параллельная стороне AC треугольника ABC, пересекает его стороны AB и BC соответственно в точках M и N. Найдите отношение площадей треугольников ABC и MBN, если AB = 14, AM = 8

Задача 27: Прямая, параллельная стороне AC треугольника ABC, пересекает его стороны AB и BC соответственно в точках M и N. Найдите отношение площадей треугольников ABC и MBN, если AM = 4, MB = 5.

Задача 28: Высота прямоугольного треугольника, проведённая из вершины прямого угла равна 15 см, один из катетов равен 17 см. Найдите гипотенузу.

ХХХ Задача 29: В прямоугольном треугольнике высота, проведённая к гипотенузе, равна 7,2 см. Найдите гипотенузу, если больший из отрезков, на которые высота делит её, равен 9,6 см

Задача 30: Продолжения боковых сторон трапеции ABCD пересекаются в точке M. Известно, что BC = 4, AD = 10. Найдите отношение площадей треугольников BMC и AMD.

XXX Задача 31: В треугольнике ABC параллельно стороне AC проведена прямая, пересекающая стороны AB и BC в точках D и E соответственно. Найдите BC, если BD = 10, AB = 25, BE = 8.

ХХХ Задача 32: В треугольниках АВС и NКP ∠В = ∠К, BС = 20 см, AB = 10 см, NK = 8 см, KP = 16 см, NP = 12 см. Найдите AС.

XXX Задача 33: На одной стороне угла O отложены отрезки OA = 9, OB = 18. На другой стороне угла отложены отрезки OD = 6, OC = 12. Найдите DC, если AB = 7.

ХХХ Задача 34: В параллелограмме АВСD проведена прямая из вершины В. Она пересекает прямую АD в точке K, сторону DС в точке E так, что CD = 24 см, DK = 8 см, СE = 14 см. Найдите ВС.

XXX Задача 35: Стороны угла O пересечены параллельными прямыми AВ и СD так, что точки A и С лежат на одной стороне угла, а точки В и D лежат на другой стороне угла. Найдите ВD, если АВ = 7 см, OB = 12 см, CD = 21 см.

ХХХ Задача 36: В трапеции АВСD с основаниями ВС и AD диагонали пересекаются в точке О так, что CО = 8 см, ВС = 15 см, АD = 25 см. Найти АО