Площадь фигур, свойство аддитивности
Площадь - это численная характеристика геометрической фигуры, показывающая размер этой фигуры:
1) Единица площади: Площадь единичного квадрата $1$ х $1$ равна $1$.
2) Cвойство аддитивности: Площадь фигуры равна количеству покрывающих её равных квадратиков ,
- Сколько единичных квадратиков покроют фигуру, столько и есть площадь этой фигуры.
- Даже если какие-то квадратики пришлось "порезать" и пересобрать в другом порядке.
- Если фигура состоит из кусков с уже известными площадями 17 и 25, то площадь этой фигуры = 17 + 25 = 32.
Площадь фигуры величина положительная , её численное значение обладает следующими свойствами:
- равные фигуры имеют равные площади ;
- площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
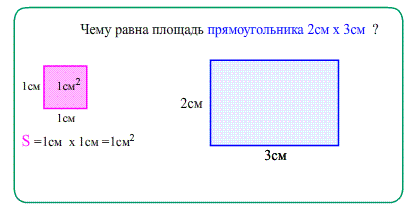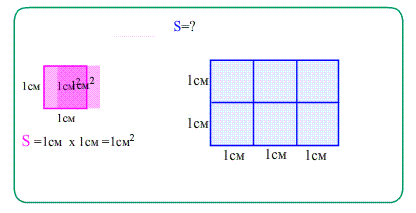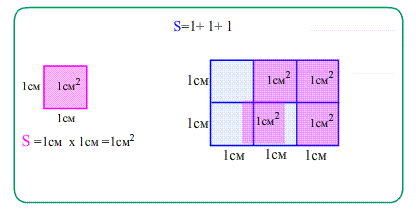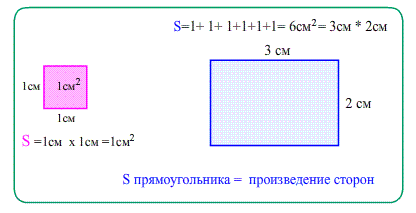
- площадь квадрата, построенного на единичном отрезке, равна единице.
- Измеряется площадь в квадратных единицах ($см^2$ , $м^2$ ), как сумма элементарных квадратиков со стороной $1$ .
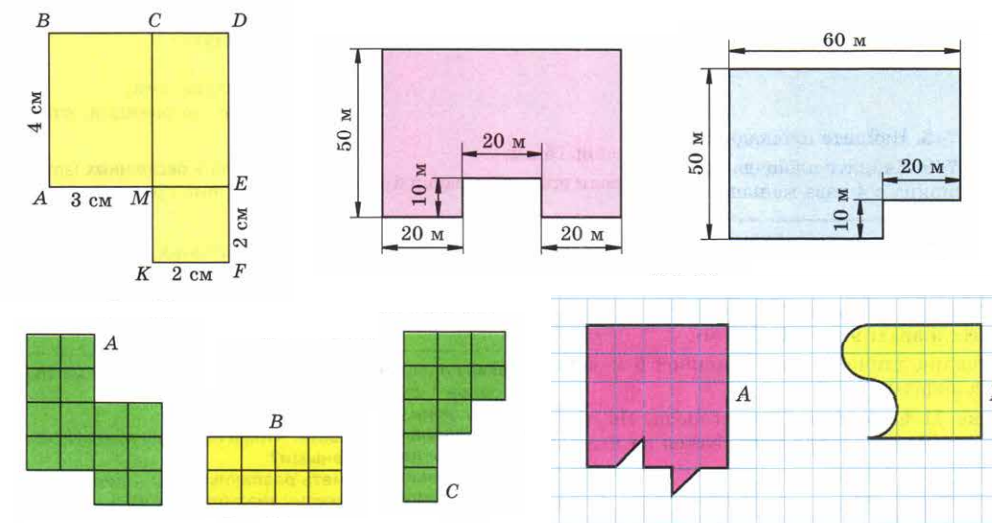
- Свойство аддитивности позволяет вычислять площадь не только по формуле суммы, но и по формуле разности.
- Можно достроить искомую фигуру до прямоугольника, найти площади всех получившихся дополнительных фигур и площадь самого прямоугольника.
- Площадь искомой фигуры равна Площадь прямоугольника минус Сумма площадей всех лишних фигур.
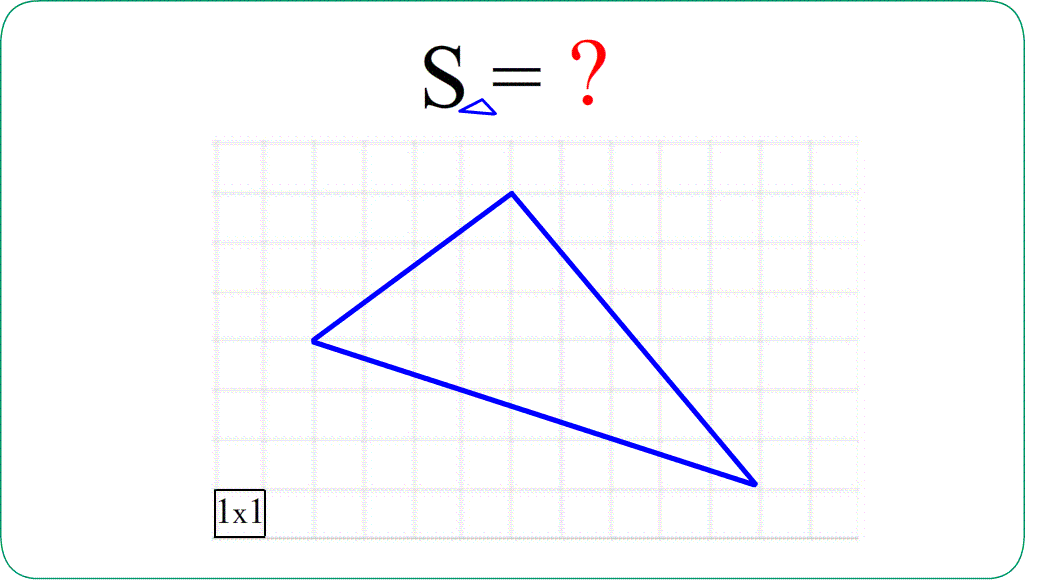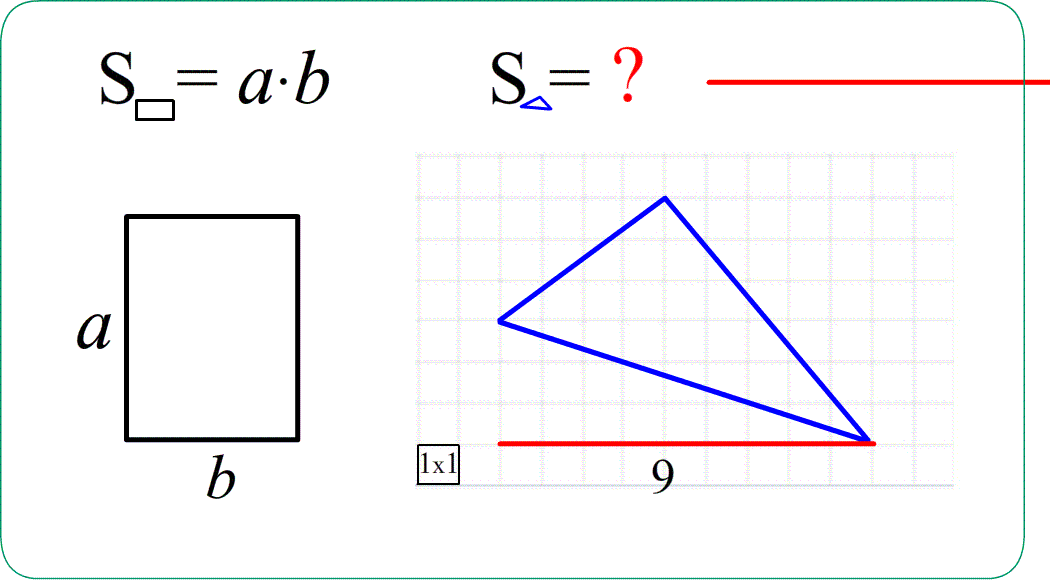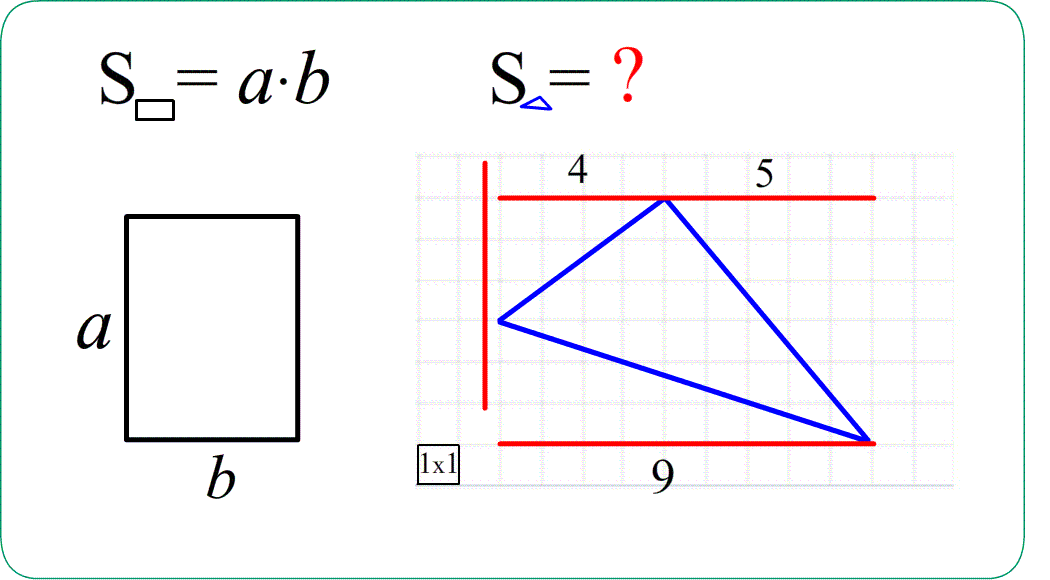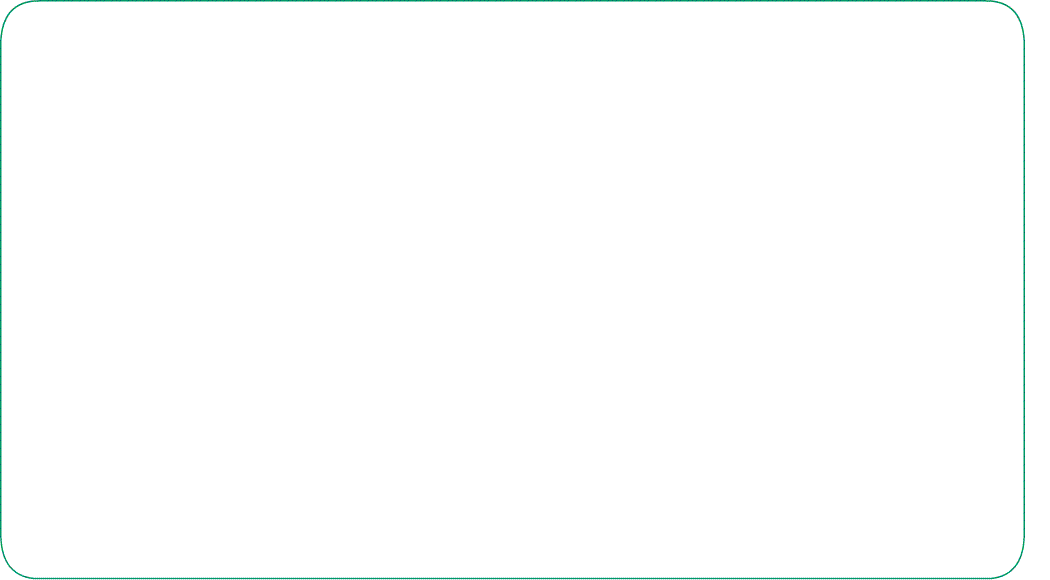
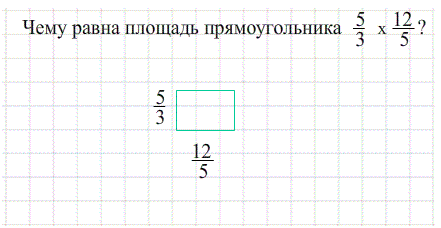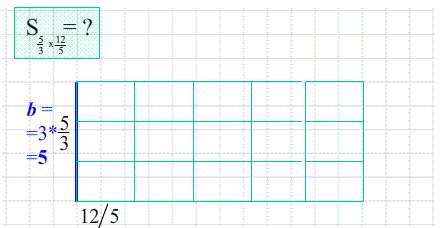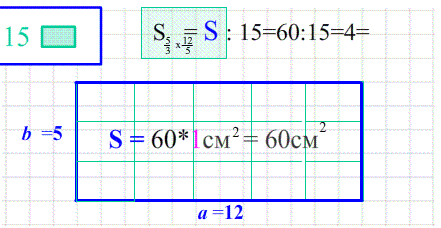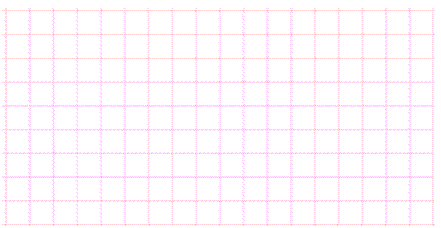
Формулы площадей фигур
Площадь прямоугольника равна произведению ширины на высоту, т.е. произведению его сторон.:
- ширина показывает сколько квадратиков в каждой строке, а высота - сколько таких строк помещается.
- Перемножение количества строк на количество квадратиков в каждой полосе - это и есть произведение сторон прямоугольника.
- Осмыслите: для целых значений сторон нужно подсчитать покрытие всего прямоугольника единичными квадратиками.
- Осмысление даже при дробных значениях сторон ...... через умножение и деление ... т.е. "много одинаковых" ...
_____________________________________________________________________________________
Теорема Площадь прямоугольника $S_{ABCD}=a\cdot b$ .
Площадь равна произведению сторон (столько квадратиков покрывают прямоугольник) .
_____________________________________________________________________________________
Иллюстрации понятия площади:
- площадь зеленного квадрата $S_{ABCD}=4$ потому, что содержит $4$ квадрата $1х1$ ;
- площадь сиреневого прямоугольника $S_{ABCD}=36$ потому, что состоит из $36$ квадратиков;
- .... или рассуждаем через произведение ширины на высоту $S=a\cdot b$ $\Rightarrow$ $9 х 4 =36$ ;
- площадь зеленой фигуры $38$ , потому как содержит ровно $38$ квадратов $1х1$ или достраиваем её до прямоугольника и :
- .... $S_{DCBALKHGFE}=S_{DENM}-S_{MCBA}-S_{LKHGFN}=6\cdot10-2\cdot4-\left(2\cdot5+2\cdot2\right)= 38$ (разность кусков) ;
- площадь синей фигуры как Разность между целым и кусочками = $6\cdot10-2\cdot5-1\cdot2= 48$
- .... если посчитать единичные квадратики - их в фигуре ровно $48$ ;
- площадь сиреневого $\bigtriangleup ABC$ равна половине $S_{ANBC}$ , потому что этот прямоугольник состоит из двух равных $\bigtriangleup ABC$ и $\bigtriangleup ANB$ ,
- значит $S_{AMBC}=S_{ABC}+S_{AMB}=2\cdot S_{ABC}$ и тогда $S_{ABC}=\frac{S_{AMBC}}{2} =\frac{4\cdot7}{2}$ ;
- из таких же соображений аддитивности $S_{ABC}=S_{ANBC}-S_{ANB}-S_{CBM}=4\cdot9-\frac{4\cdot9}{2}-\frac{4\cdot3}{2}$ ;
- $S_{ABC}=14$ еще и потому , что $\bigtriangleup ABC$ можно "покрыть" ровно $14$-ью квадратиками,
- хотя для этого и пришлось некоторые порезать на кусочки и составить из них мозаику.
- синий треугольник можно выложить "как пазл" из $12$-ти квадратиков $1х1$ , предварительно порезав на нужные кусочки.
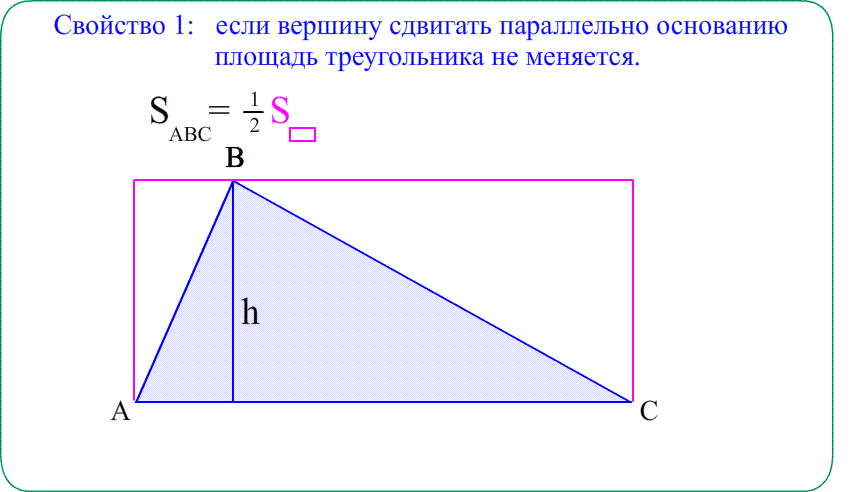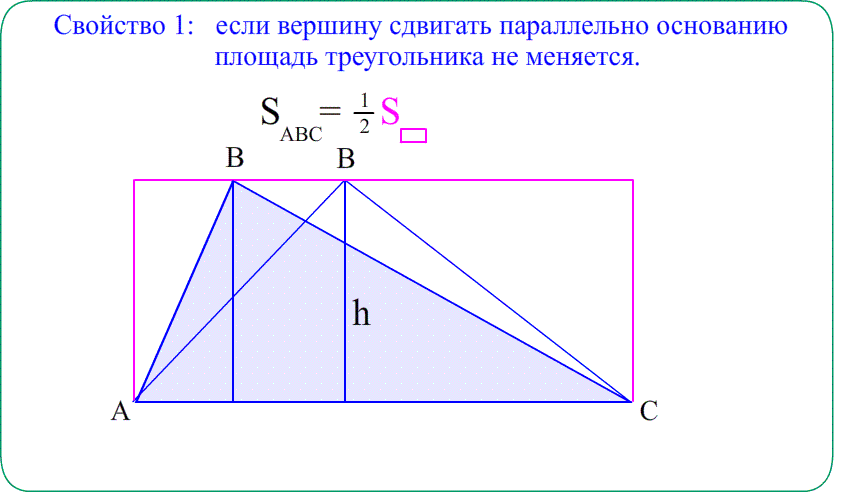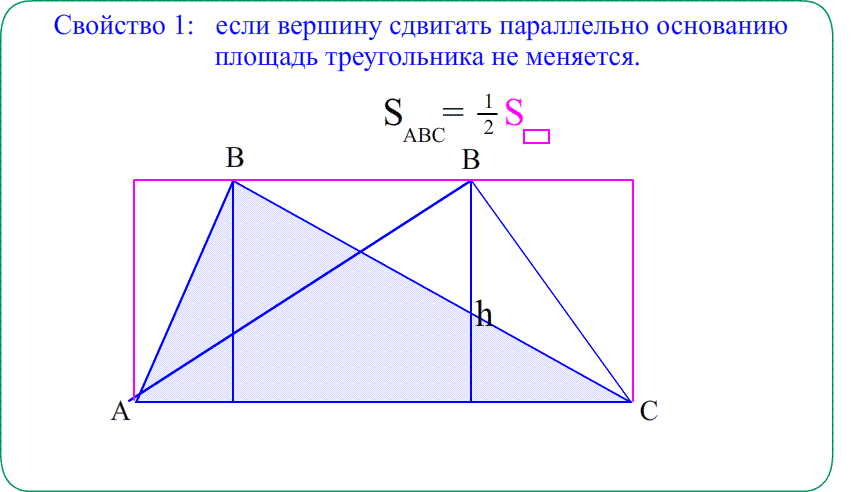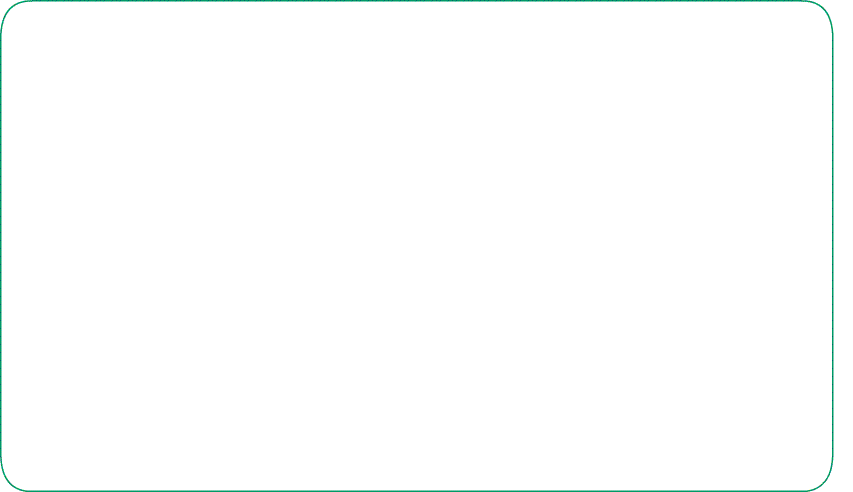
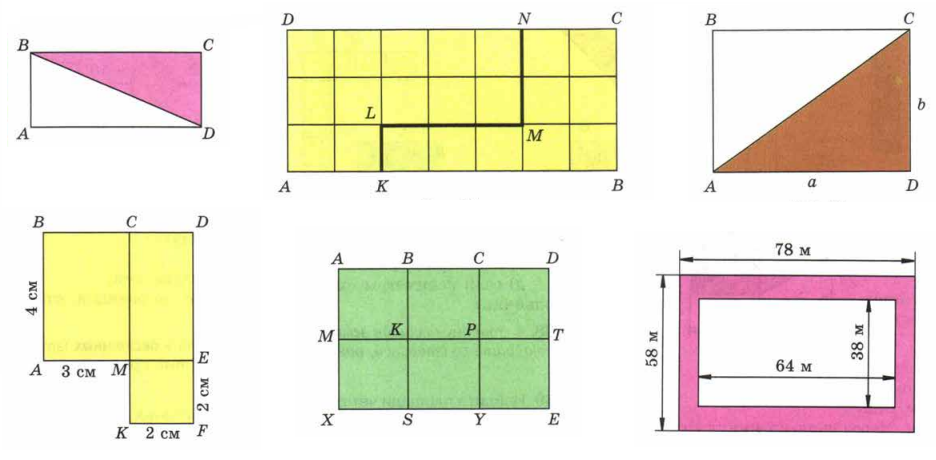
Главное свойство: Сумма площадей кусков фигуры равна площади целой фигуры.
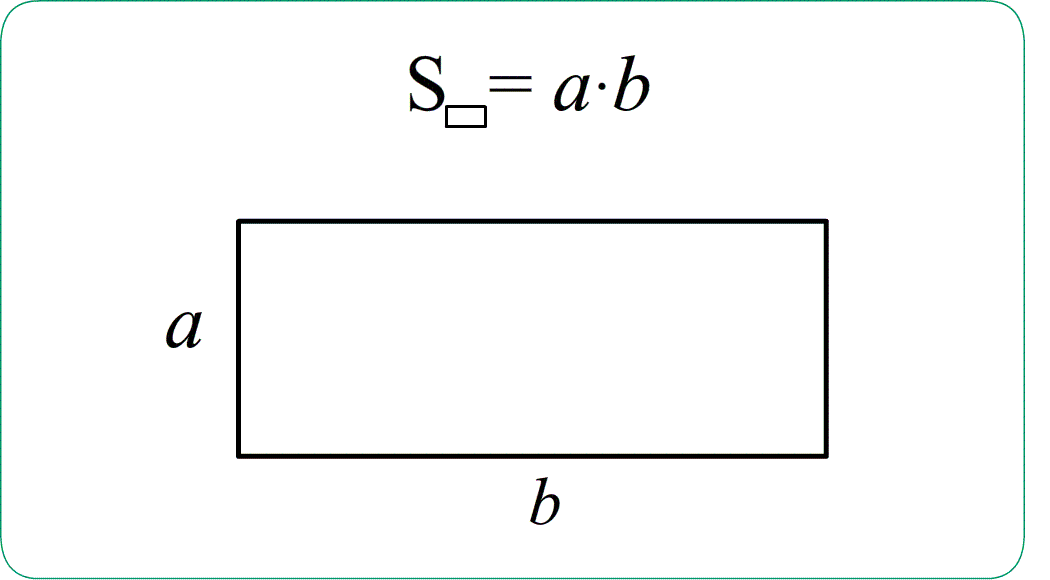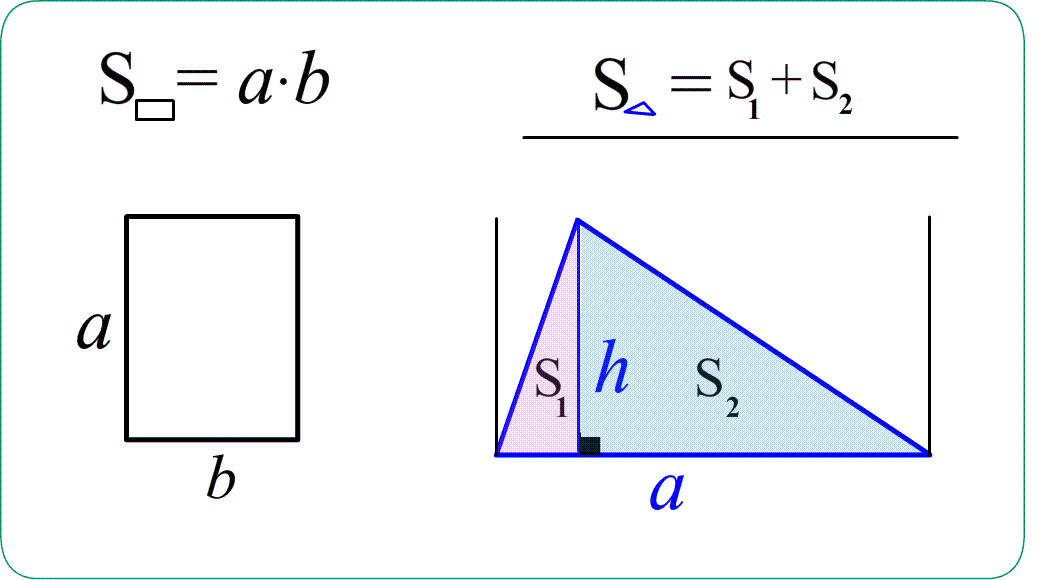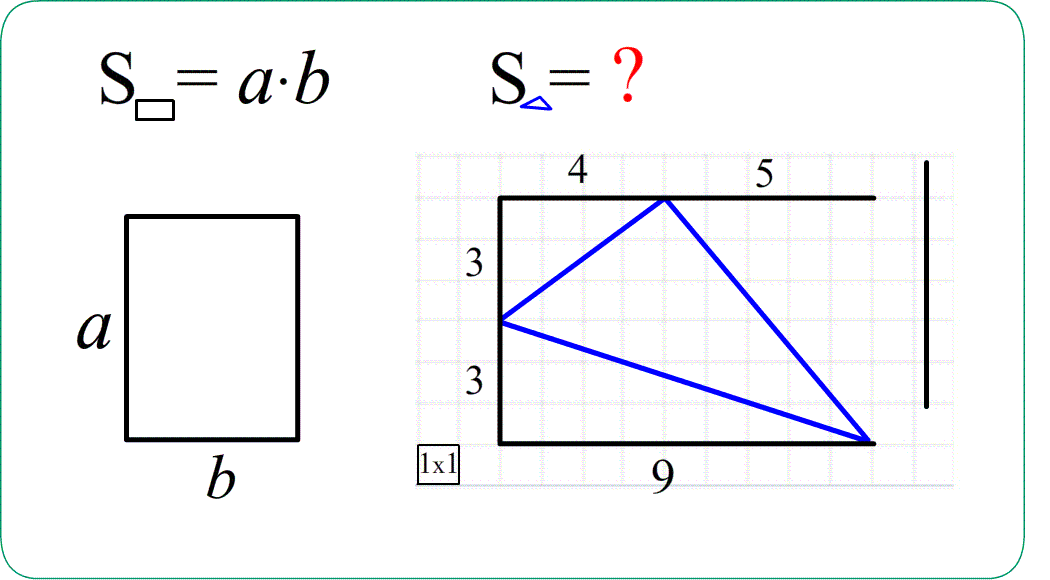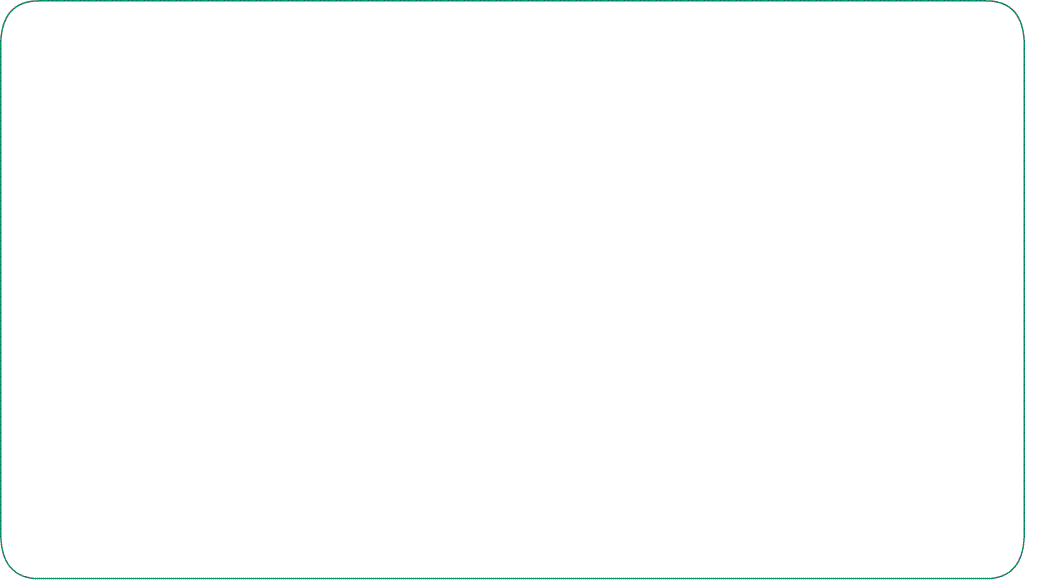
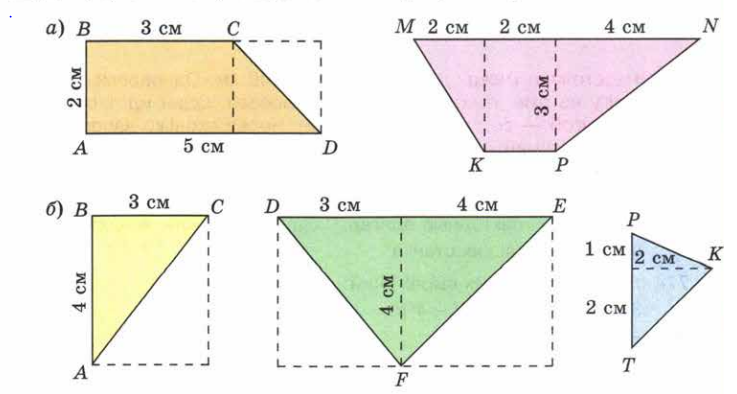
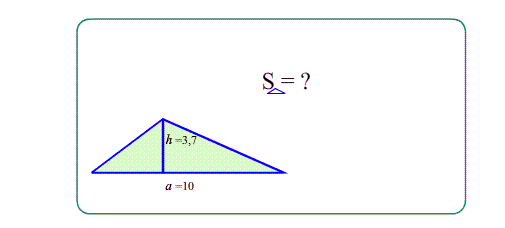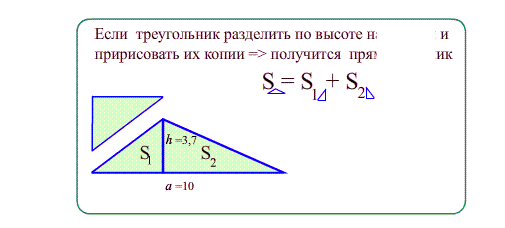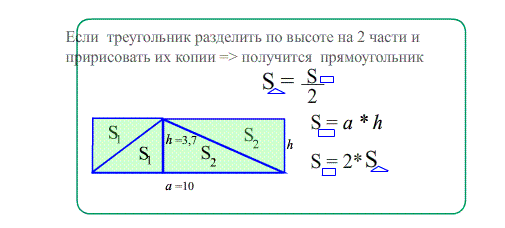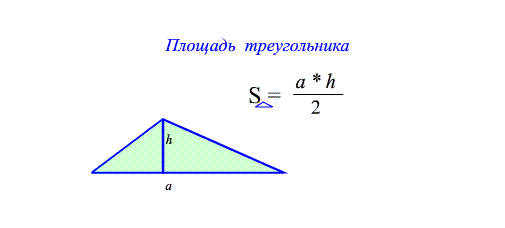
Задача 1. Найти площади изображенных на рисунках фигур. Использовать свойства "складывания площадей", "вычитания площадей", "формулу площади треугольника", "равные фигуры - равные площади", "половина фигуры - половина площади".
_____________________________________________________________________________________
Теорема Площадь квадрата равна квадрату его стороны.
_____________________________________________________________________________________
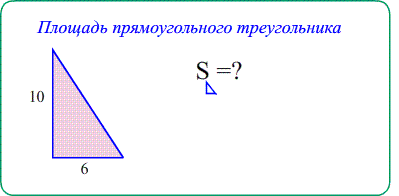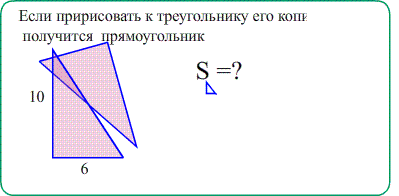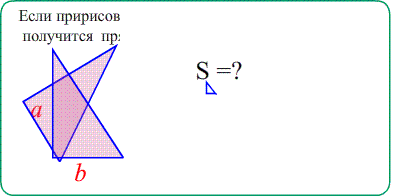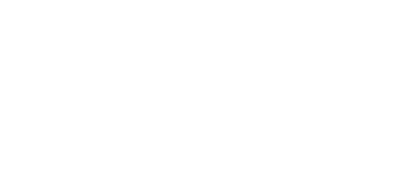
Теорема Площадь прямоугольного треугольника $S_{ABC}=\frac{a\cdot b}{2}$ - "половина произведения катетов" ,
"половина площади обрамляющего прямоугольника"
_____________________________________________________________________________________
_____________________________________________________________________________________
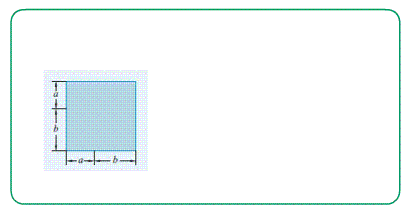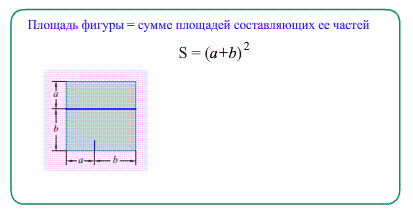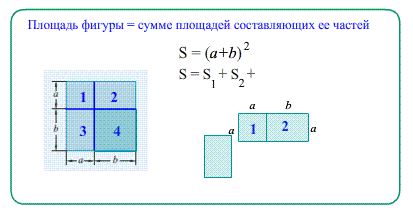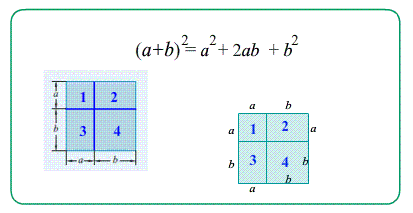
Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов $c^2=a^2+b^2$
_____________________________________________________________________________________
- Теорема Пифагора доказывается через осмысление площадей частей и целого, с помощью сконструированной фигуры .....
- Сконструируем прямоугольник так: В углах расставим прямоугольные треугольники так, чтоб они составляли один большой прямоугольник.
- Сторона большого прямоугольника состоит из отрезков - катетов прямоугольного треугольника, т.е. равен сумме катетов.
- А внутри прямоугольника "будет сидеть" квадрат со стороной, равной гипотенузе прямоугольного треугольника.
- Площадь внутреннего квадрата равна площадь большого прямоугольника минус четырежды площадь прямоугольного треугольника.
- С другой стороны, Площадь внутреннего квадрата равна квадрату гипотенузы. По формуле площади квадрата.
- Значит, эти числа равны: $\left(a+b\right)^2-4\cdot\frac{ab}{2}=c^2$. Отсюда и получается Теорема Пифагора.
- Через понятие площади так же можно вывести Формулы сокращенного умножения .
Задача 2. Трапеция имеет основания 10 и 6, высоту 5. Какой наибольший прямоугольник со стороной 6 можно вписать внутри трапеции. Чему равна его площадь. Какой наименьший прямоугольник со стороной 10 будет обрамлять трапецию снаружи. Какова его площадь. Укажи два числа, между которыми заключена площадь самой трапеции.
- Наибольший прямоугольник со стороной 6 будет опираться на меньшее основание и "продолжаться" до большого основания.
- Наименьший прямоугольник со стороной 10 будет опираться на большее основание и содержат в себе всю трапецию.
- Площади этих прямоугольников можно расчитать по формуле "ширина на высоту".
- Свойство площадей: если одна фигура полностью содержится внутри бругой, то ее площадь меньше.
- Визуально сравним площади трапеции и полученных прямоугольников. Что больше, что меньше?
Задача 3. В треугольнике $ABC$ $\angle BAC$ - прямой, $AB$ и $AC$ равны соответственно $1$ и $3$ . Точка $K$ делит сторону $AC$ в отношении $7:1$, считая от точки $A$. Что больше: длина $AC$ или длина $BK$ ?
- Решение: Чтобы найти $BK$, которая является гипотенузой в треугольнике $ABK$, нужно знать длину катета $AK$ .
- Найдем отрезок как долю стороны: $AK=\frac{7}{8}AC=\frac{7}{8}\cdot 3=2,625$ .
- Теперь для треугольника $ABK$ составим теорему Пифагора $BK^2=AB^2+AK^2$
- Выразим отрезок из равенства: $BK=\sqrt{ AB^2+AK^2}=\sqrt{1+\frac{441}{64}}=\sqrt{\frac{505}{64}}$ .
- Осталось сравнить числа $\sqrt{\frac{505}{64}}$ и $3$.
- Представим последнее как $3=\sqrt{9}=\sqrt{\frac{9\cdot64}{64}}=\sqrt{\frac{576}{64}}$ . Ответ: $AC>AB$
Задача 4. В прямоугольнике $ABCD$ длины отрезков $AB$ и $BD$ равны соответственно $2$ и $\sqrt{7}$. Точка $M$ делит $CD$ в отношении $1:2$, считая от точки $C$. $K$ – середина $AD$. Что больше: длина $BK$ или длина $AM$ ?
- Решение: Определим сначала $BK$ , для этого найдем $AK$:
- $AB^2+AD^2=BD^2$ , $AD^2= BD^2- AB^2$ , $AD=\sqrt{ BD^2- AB^2}=\sqrt{7-4}=\sqrt{3}$ , $AK=\frac{1}{2}AD=\frac{\sqrt{3}}{2}$
- Теперь переходим к $\bigtriangleup ABK$, где $BK$ – гипотенуза $BK^2=AB^2+AK^2$ $\Rightarrow$ $BK=\sqrt{ AB^2+AK^2}=\sqrt{4+\frac{3}{4}}=\sqrt{\frac{19}{4}}$ .
- Найдем теперь $AM$: $MD=\frac{2}{3}CD=\frac{2}{3}\cdot 2=\frac{4}{3}$ , $AM=\sqrt{AD^2+MD^2}=\sqrt{3+\frac{16}{9}}=\sqrt{\frac{43}{9}}$ .
- Осталось сравнить дроби $\frac{19}{4}$ и $\frac{43}{9}$. Приведение к общему знаменателю: $\frac{19}{4}=\frac{171}{36}$ и $\frac{43}{9}=\frac{172}{36}$.
- Таким образом, длина $AM$ больше длины $BK$. Ответ: $AM>BK$
Еще о площадях фигур
Две фигуры называются равновеликими, если у них одинаковые, равные площади.
Способ получения или доказательства формулы площади той или иной фигуры состоит в "разрезании" этой фигуры на кусочки и "пересобирании" этих кусочков так, чтобы получилась фигура с уже известной площадью. Если эти кусочки не перекраиваются, то из свойства аддитивности: фигура до разрезания и фигура после "собирания" будут равновеликими.
Например, от трапеции можно отрезать 2 треугольника и приставить так, что получится прямоугольник. От параллелограмма можно отрезать треугольник и приставить в другом месте и опять же получится известный прямоугольник или же параллелограмм диагональю разделится на 2 треугольника.
Любой треугольник высотой "режется" на два прямоугольных треугольника. Прямоугольные треугольники (одинаковые), в свою очередь, получаются путем разрезания прямоугольника по диагонали. Каждый раз площадь осмысливается через площади либо кусочков, либо той фигуры, "собранной" этих кусочков , т.е. путем активного использования
свойства аддитивности площади.
В итоге, получается единный взгляд на понятие площадь фигуры, как "переcбор" составляющих кусочков:
Площадь "прямой" фигуры равна произведению "усредненной ширины" на высоту или $S=a\cdot h$.
Площадь "остроконечной" фигуры равна половине произведения "средней ширины" на высоту: $S=\frac{1}{2}\cdot a\cdot h$
- "Прямые фигуры" - прямоугольник, параллелограмм, квадрат, ромб, четырехкгольник, трапеция
- "Остроконечные фигуры": пробa треугольник, сектор, круг, трапеция(гибрид)
Интерактивные Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 51: Площадь прямоугольника АВСD равна 80 см2, К, М, N, Р – середины его сторон. Найдите площадь четырёхугольника КМNР.
Задача 52: Один катет прямоугольного треугольника в 3 раза больше другого. Площадь треугольника равна 24 см2. Найдите больший катет этого треугольника.
Задача 53: Гипотенуза прямоугольного треугольника равна 18 см. Один из острых углов в 2 раза меньше другого. Найдите катет, лежащий против большего из острых углов.
Задача 54: Площадь прямоугольного земельного участка равна 20 га. Длина этого участка равна 500 м. Найдите ширину этого участка.
Задача 55: Найдите периметр и площадь ромба, если его диагонали равны 12 см и 16 см
Задача 56: Диагонали ромба равны 24 см и 36 см. Найдите площадь ромба.
Задача 57: Стороны треугольника 7, 24 и 25. Определите его вид и вычислите площадь треугольника.
Задача 58: Одна из диагоналей ромба равна 48, а его сторона равна 25. Найдите площадь ромба.
Задача 59: Боковая сторона равнобедренного треугольника равна 41, а его основание равно 18. Найдите площадь треугольника.
Задача 60: Основание равнобедренного треугольника равно 48 см. Высота, проведённая к основанию равна 10 см. Найдите боковую сторону треугольника и высоту к ней.
Задача 61:
Задача 62: