Пересечение двух параллельных прямых одной секущей
Параллельными называется пара прямых, которые при продолжении не пересекаются.
- Когда две паралелльные прямые $a$ и $b$ пересекаются секущей $c$ , то образуется много разнообразных углов.
- Некоторые пары углов имеют свои имена - названия:
пара накрест лежащие углы : ∠3 и ∠5, ∠4 и ∠6;
пара односторонние углы : ∠4 и ∠5, ∠3 и ∠6;
пара соответственные углы : ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.
Свойства углов, образованных при пересечении секущей с двумя параллельными (трансверсаль):
- накрест лежащие углы равны: ∠ 3 = ∠5, ∠ 4 = ∠6.
- соответственные углы равны: ∠ 1 = ∠ 5, ∠ 4 = ∠ 8, ∠ 2 = ∠ 6, ∠ 3 = ∠ 7.
- сумма односторонних углов равна 180 градусов: ∠ 3 + ∠ 6 = 180 $^o$, ∠ 4 + ∠ 5 = 180 $^o$.

Теорема Если две параллельные линии пересекаются третьей (Секущей), тогда выполняются:
ТеоремаТеорема * накрест лежащие углы равны ;
ТеоремаТеорема * соответственные углы равны ;
ТеоремаТеорема * сумма односторонних углов 180 град. ;
ТеоремаТеорема * вертикальные равны ∠3 = ∠1, ∠8 = ∠6 .
Накрест-лежащие, = = , Z-образ: От концов отрезка-секущей два параллельных отрезка уходят в разные стороны.

Односторонние, +=180, П-образ: От концов отрезка-секущей два параллельных отрезка уходят в одну сторону.

Соответственные, = =, F-образ: От концов луча-секущей два параллельных отрезка уходят в одну сторону.

- Чтоб увидеть пары таких углов (накрест-лежащих, односторонних, соответственных), надо увидеть две параллельные и отрезок секущей с концами в точках, лежащих на этих параллельных. Т.е. увидеть трансверсаль!
- Вершины таких углов находятся в разных концах отрезка-секущего.
- Пары смежных (вертикальных) углов имеют одну, общую вершину.
Смежные, +=180, Т-образ: От точки отрезка исходит луч, 2 примыкающих угла. Общая вершина.

Вертикальные, = =, Х-образ: При пересечении двух отрезков возникающие противоположные 2 угла. Общая вершина.

Свойства параллельных прямых, признаки параллельности:
2-х перпендикулярных: Если 2 прямые одновременно перпендикулярны к третьей, то они параллельны друг другу.
Односторонных углов: Если 2 прямые не параллельны, то равенства не выполняются: 3 + 6 < 180 ; 4 + 5 > 180 .
Ассоциативность: Если 1-ая прямая параллельна 2-ой, а 2-ая параллельна 3-й, то 1-ая прямая параллельна 3-й.


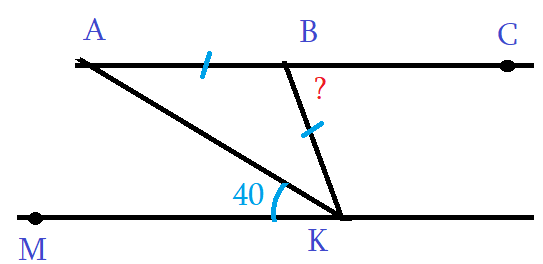
Задача 1: На рисунке АС и МК параллельны, отрезки АВ = ВК равные. Дан угол ∠АКМ = 40°. Найти ∠КВС.
- Решение: АС ║ МК параллельны, АК - секущая, $\Rightarrow$ ∠АКМ и ∠КАВ накрест лежащие, $\Rightarrow$ ∠КАВ = 40°.
- ∆АВК – равнобедренный, АВ = ВК $\Rightarrow$ углы у основания ∠КАВ = ∠АКВ значит, $\Rightarrow$ ∠АКВ = 40°.
- Значит, углы ∠АКВ = ∠АКМ равные. Угол ∠МКВ состоит из частей, аддитивность, ∠МКВ = ∠АКВ + ∠АКМ = 80°.
- АС ║ МК параллельны, АК - секущая, $\Rightarrow$ ∠ВКМ и ∠КВС накрест лежащие, $\Rightarrow$ Ответ: ∠КВС = 80°.
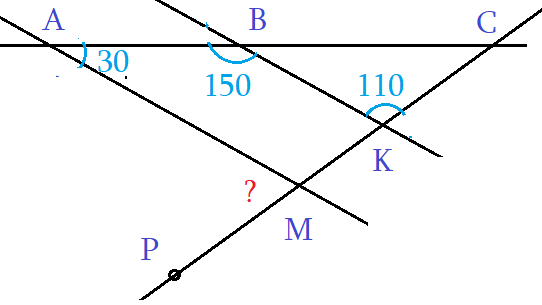
Задача 2: На рисунке, даны углы ∠ВАМ = 30°, ∠АВК = 150°, ∠ВКС = 110°. Найти ∠АМР.
- Решение: Углы ∠ВАМ и ∠АВК - односторонние от секущей АВ. Их сумма ∠ВАМ + ∠АВК = 180°.
- Сумма односторонних 180°? ... по теореме "о параллельных", прямые АМ и ВК должны быть параллельными. АМ ║ ВК.
- Теперь: АМ ║ ВК, СР - секущая. Односторонние углы равные, ∠ВКС = ∠АМК. Значит, ∠АМК = 110°.
- Наконец, углы ∠АМК и ∠АМР - смежные. Значит, ∠АМК + ∠АМР = 180°. $\Rightarrow$ ∠АМР = 180° - ∠АМК = 70°.
- Ответ: ∠АМР = 70°. Замечание: "надо видеть все секущие к параллельным, и углы к ним".
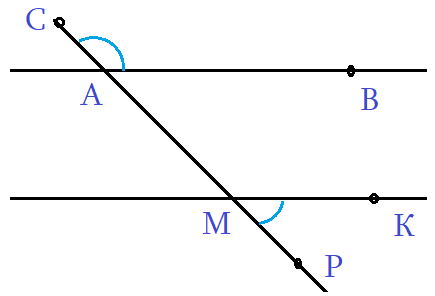
Задача 3: На рисунке, АВ параллельно МК, угол ∠РМК составляет треть угла ∠САВ. Найти эти углы.
- Решение: Дано: отношение углов ∠РМК : ∠САВ = 1 : 3. Выразим: ∠САВ = 3∠РМК
- Как связаны искомые углы по рисунку? ∠САВ и ∠МАВ - смежные, значит ∠МАВ = 180° - ∠САВ.
- Углы ∠МАВ и ∠РМК односторонние углы при параллельных АВ ║ МК и секущей РС. Значит, ∠МАВ = ∠РМК
- Из двух равенств получаем ∠РМК = 180° - ∠САВ. Вспомним ∠САВ = 3∠РМК, подставим: ∠РМК = 180° - 3∠РМК
- ∠РМК = 45°, значит ∠САВ = 3∠РМК = 135°. Ответ: 45°, 135°
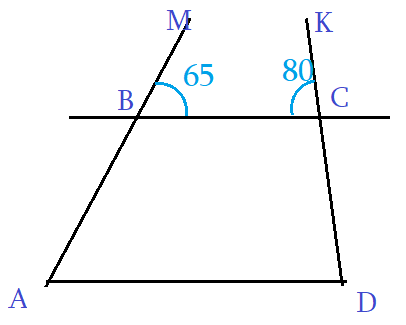
Задача 4: На рисунке, АD параллельно ВС, угол ∠МВС = 65°, ∠ВСК = 80°. Найти углы четырехугольника АВСD.
- Трапеция АВСD: Четырехугольник с двумя параллельными сторонами называется трапецией. АD ║ ВС.
- Решение: Угол трапеции ∠АВС смежен с ∠МВС, значит ∠АВС = 180° - ∠МВС = 115°.
- Аналогично, угол трапеции ∠ВСD смежный к углу ∠ВСК, значит ∠ВСD = 180° - ∠ВСК = 100°.
- АМ секущая к АD ║ ВС $\Rightarrow$ ∠ВАD и ∠МВС соответственные, значит равные ∠ВАD = ∠МВС = 65°.
- Аналогично, КD секущая к АD ║ ВС $\Rightarrow$ ∠АDС и ∠ВСК соответственные, значит равные ∠АDС = ∠ВСК = 80°.
- Ответ: Углы трапеции ∠ВАD = 65° ∠АВС = 115° ∠ВСD = 100° ∠АDС= 80°
Задача 4, продолжение, "углы в трапеции": Пусть углы любые: ∠МВС = х, ∠ВСК = у.
- Такими же рассуждениями о смежных и односторонних, получим: ∠А = х ∠В = 180° - х ∠С = 180° - у ∠D = у
- Видно: ∠А + ∠В = 180° ∠С + ∠D = 180°. Сумма углов при боковой стороне трапеции 180° . Односторонние!
- Видно: ∠А + ∠В + ∠С + ∠D = 180°. Сумма всех углов трапеции равна 360°. . Как у четырехугольника?
Задача 5: Известны два угла треугольника. Через вершину третьего угла проведена прямая, параллельная стороне. Найти углы между этой прямой и сторонами треугольника.
- Дано: ∠ВАC = 80° ∠ACB = 30° MK ║ AС. Найти: ∠МВА = ? ∠КВС = ? ∠АВС = ?
- Есть параллельные MK ║ AС и секущая АВ. Тогда, накрест лежащие ∠МВА = ∠ВАC = 80°
- При тех же параллельных и секущей ВС также накрест лежащие равны: ∠КВС = ∠ACB = 30°
- Развернутый угол ∠МВК = 180° состоит из трех частей, аддитивность углов: ∠МВК = ∠МВА + ∠АВС + ∠КВС
- Значит, 180° = 80° + ∠АВС + 30° ∠АВС = 180° - 80° - 30° = 70° - третий угол треугольника.
- Теорема: ∠МВА + ∠АВС + ∠КВС = 180° $\Rightarrow$ ∠АВС + ∠АВС + ∠ВСА = 180° - сумма углов треугольника.
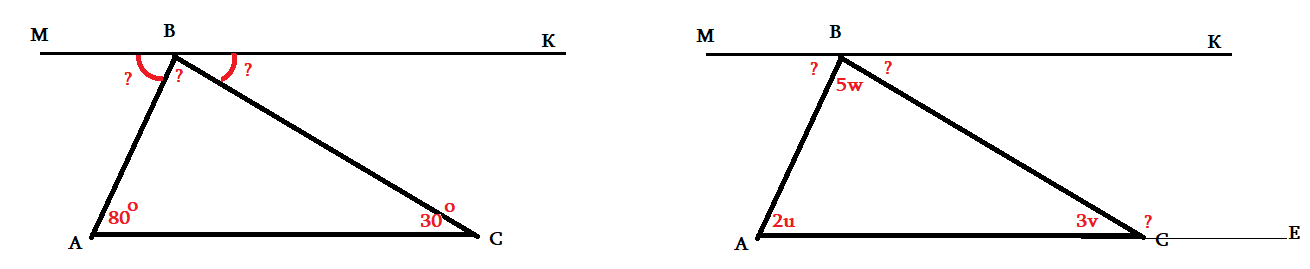
Задача 5, продолжение, "с параметрами": Углы треугольника заданны параметрически 2u, 3v, 5w. Выразить углы ∠МВА, ∠КВС и ∠АВС через параметры u, v. Выразить параметр w через другие u, v.
- Углы ∠МВА и ∠КВС можно выразить через свойство накрест-лежащих при параллельных MK ║ AС.
- Три угла ∠МВА, ∠КВС и ∠АВС складываются в развернутй угол 180°. Получим равенство с параметрами u, v, w. Выразим w
Факты, Следствия из теорем об углах при параллельных и секущей к ним:
- В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы. Что секущая?
- В паралеллограмме сумма углов у одной стороны равна 180 град. - внутренние односторонние. Что секущая?
- В трапеции сумма углов у боковых сторон равна 180 град. - внутренние односторонние. Что секущая?
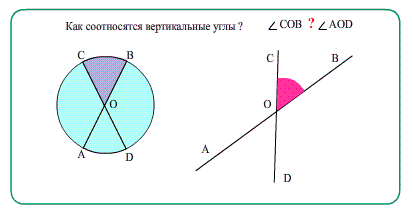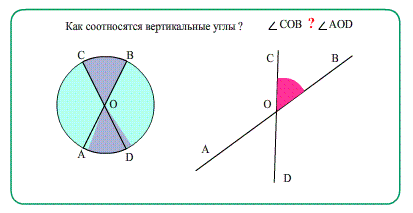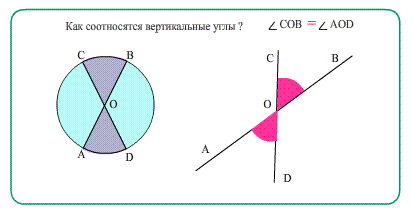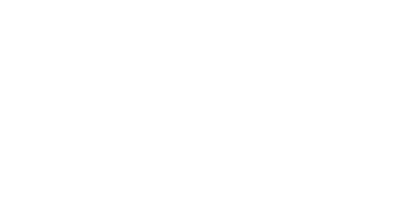
- Ещё об углах: Диаметры в окружности при пересечении образуют равные вертикальные углы.
- Сумма углов треугольника 180 градусов . Достроить параллельную, увидеть секущую!
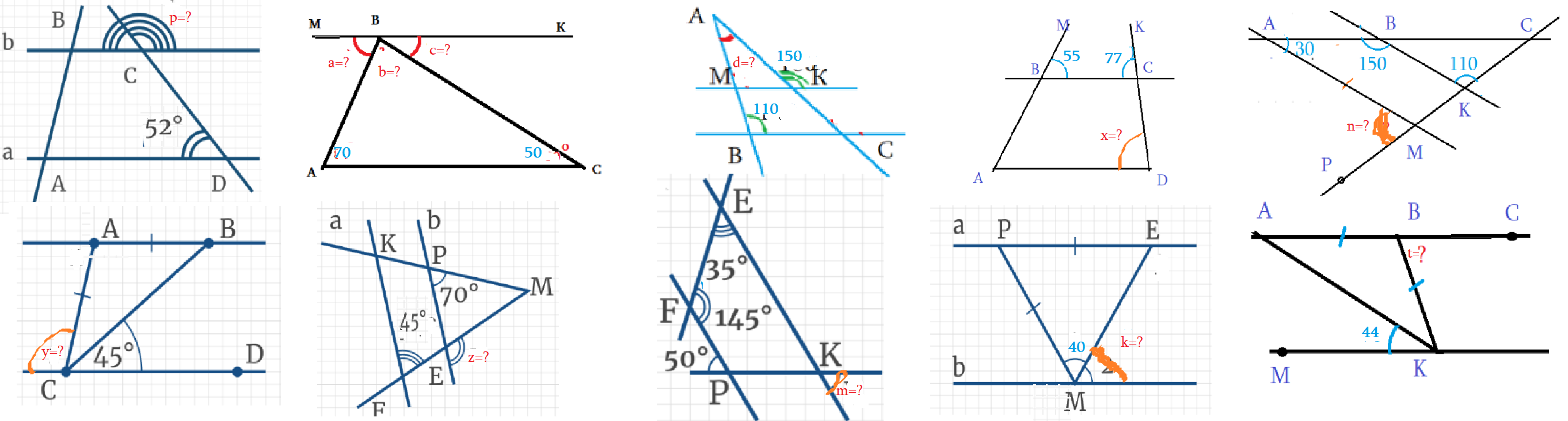
Решаем устно:
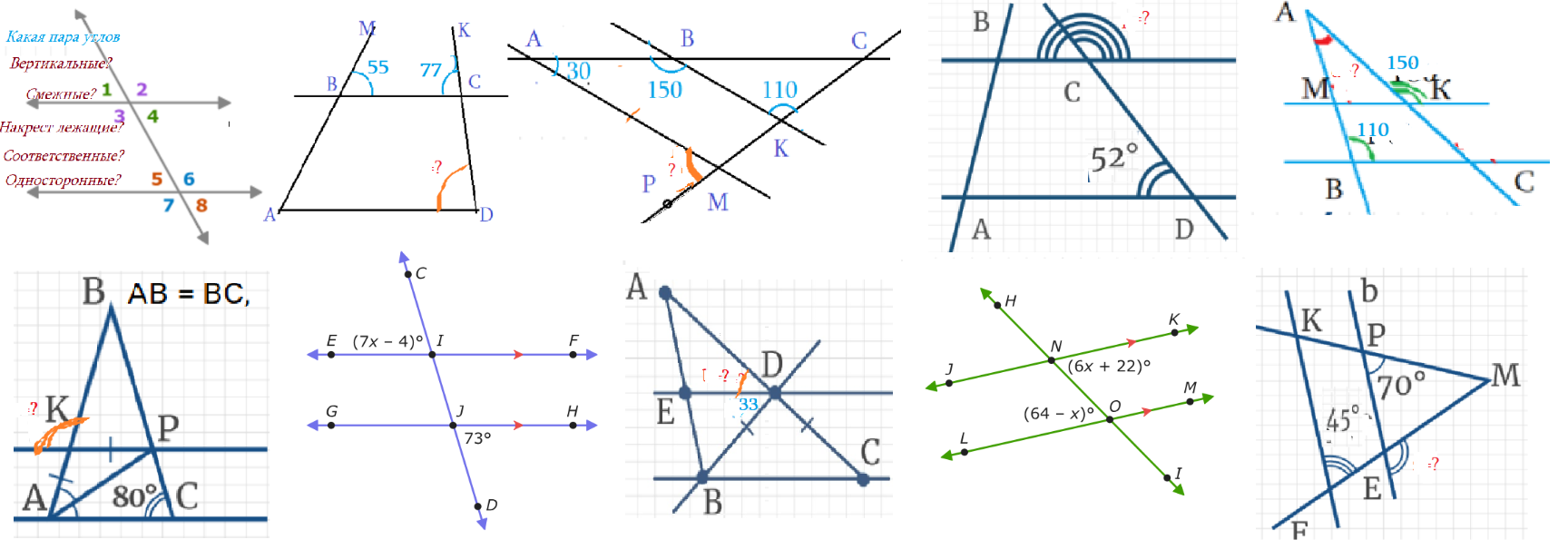
Упражнения (А):
Упражнения (В):
Упражнения (В):
Задачи из сайта МЭШ :
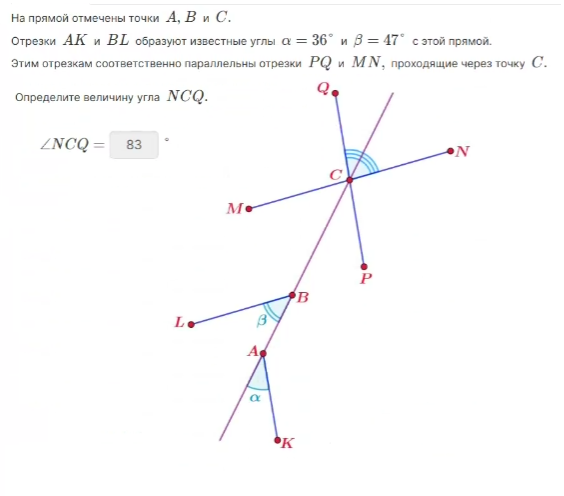

Задачи из сайта https://resh.edu.ru :
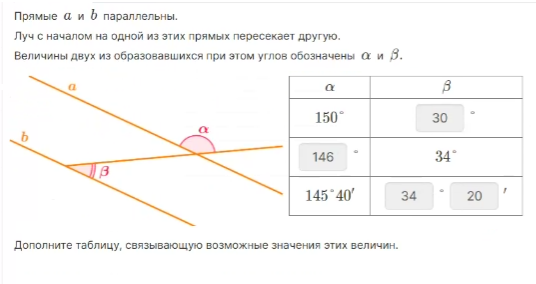
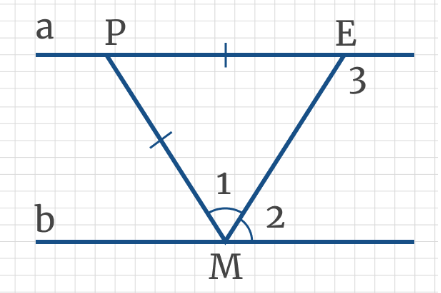
Задача 1: Установите соответствие между углами и их градусными мерами, если ∠РМЕ = 50°, а ∠1 = ∠2 и РМ = РЕ.
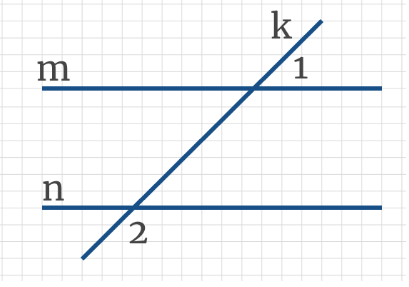
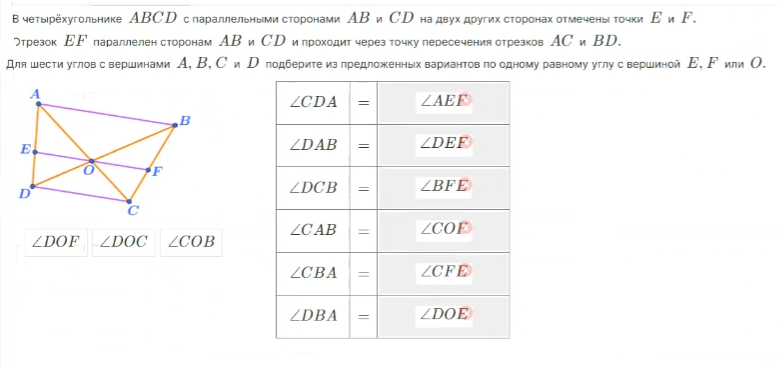
Задача 2: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 50% угла 2. Найдите угол 1.
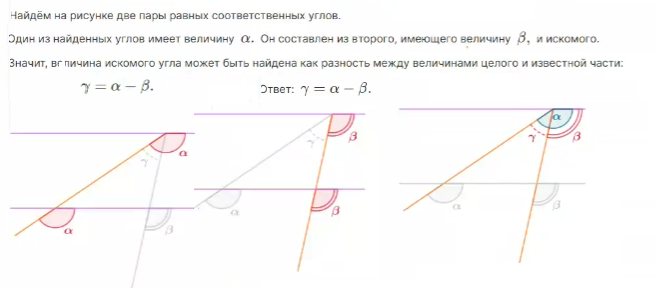
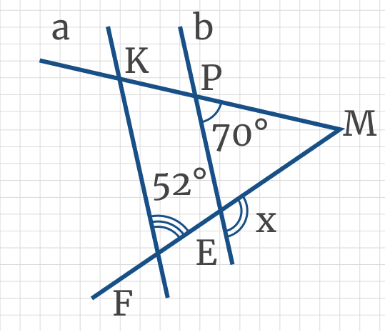
Задача 3: По рисунку найдите градусную меру неизвестного угла х. Параллельные прямые а и b пересечены секущими МК и МF.
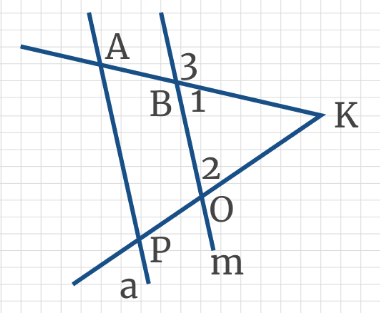
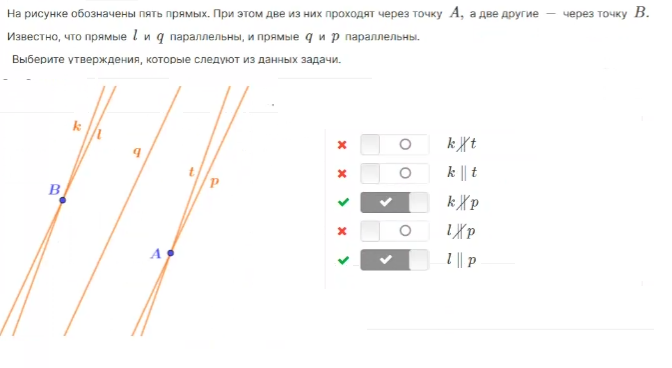
Задача 4: Прямые а и m параллельны. АК и КР – секущие, ∆ВКО – равнобедренный. ∠3 = 120°. Чему равен ∠2?
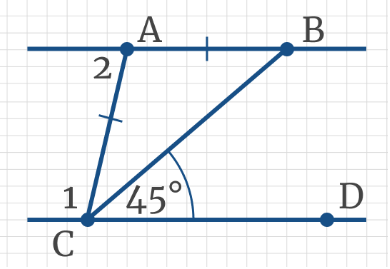
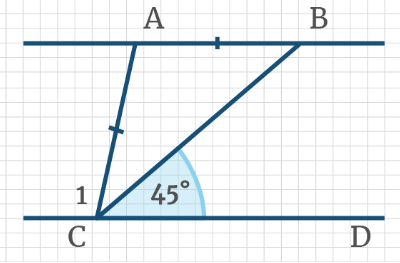
Задача 5: На рисунке прямые AB║CD, при этом AB = AC, ∠BCD = 45°. Найдите угол 2
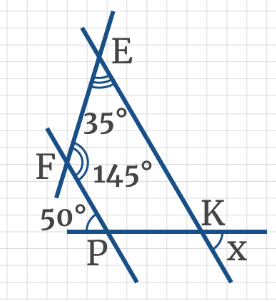
Задача 6: Прямые FP и EK параллельны, чему равна градусная мера угла x?
Задача 7: Через параллельные прямые а и b проведены секущие ВА и ВС, так что АВ = ВС, при этом ∠ВСА = 80°. Найдите градусную меру угла 1.
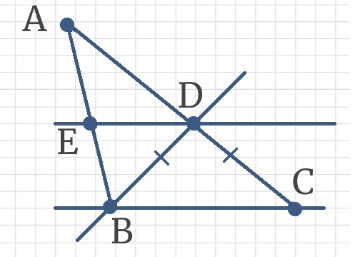
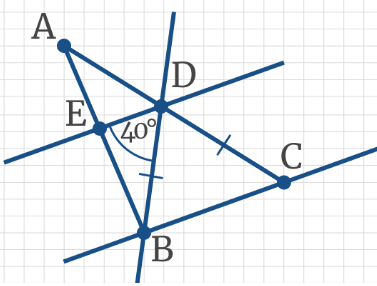
Задача 8: В треугольнике АВС BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 40°. Чему равен угол ADВ?
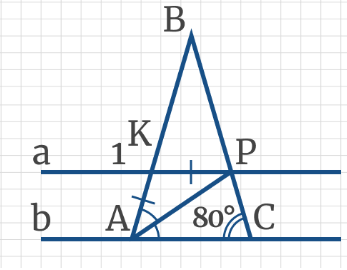
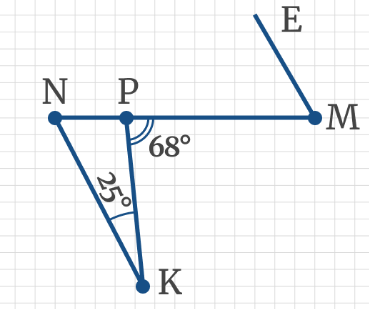
Задача 9: Прямые KN и ME параллельны. По рисунку найдите угол ЕМР, если сумма углов треугольника равна 180°.
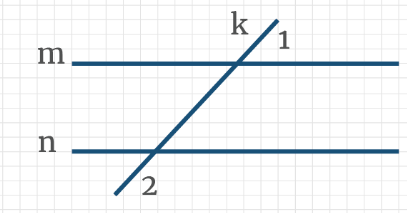
Задача 10: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 20 % угла 2. Найдите угол 1.
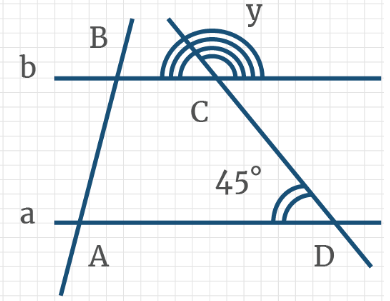
Задача 11: Прямые a и b параллельны. Основываясь на рисунке, определите, чему равна градусная мера угла y.
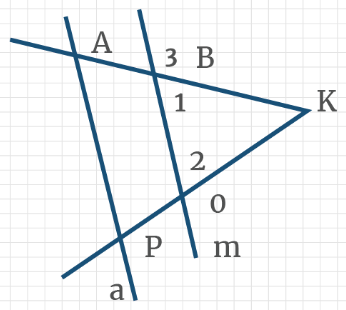
Задача 12: ∆ВКО – равнобедренный. ∠3 = 110°. Чему равен ∠2?
Задача 13: На рисунке AB║CD, при этом AB=AC, ∠BCD = 45°. Найдите угол BAC.
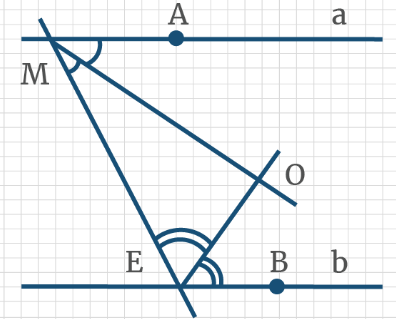
Задача 14: На рисунке прямые а║b, при этом MO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ?
Задача 15: Дан треугольник АВС. BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 50°. Чему равен угол ADE?
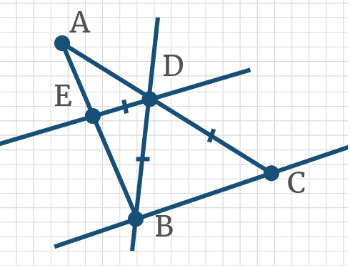
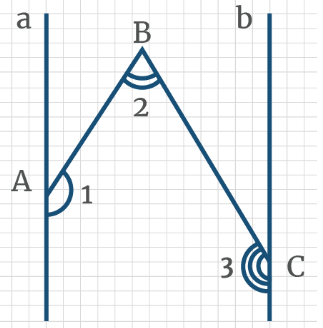
Задача 16: Прямые а и b параллельны. Чему равна градусная мера суммы углов 1, 2, 3?
Задача 17: Проведена секущая к прямым BC и DE, при этом ВD = DC, BC || DE, ∠BDE = 40°. Чему равен ∠ADE?
Задача 18: Один из односторонних углов при двух параллельных прямых и секущей на 66º меньше другого. Найдите меньший из односторонних углов.
Задача 19: Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°. Найдите, чему равен один накрест лежащий угол.
Задача 20: "углы в параллелограмме и трапеции":
-
один из углов параллелограмма 40. найти остальные
-
найти углы параллелограмма, если известно, что сумма двух 80. (100, 160)
-
найти углы параллелограмма, если известно, что разность двух 70. (110, 130)
-
Диагональ параллелограмма состовляет с одной из сторон углы 25 и 35. найти все углы параллелограмма
-
Углы параллелограмма относятся как 2:3 найти все углы
-
Чему равны углы равнобедренной трапеции, если разность противолежащих 40