Ромб - это параллелограмм, у которого все стороны равны.
- "Чтоб Выучить, распознать нечто стоящее - узнать его в движении, при изменениях"
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей - ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали - новый ромб совпадет с прежним. Симметрия.
Замечание: Если "зряче видим" центральную и осевые симметрии ромба, то все его свойства у нас "в кармане".
Свойства ромба:
- Ромб симметричен относительно точки O - пересечения диагоналей. O - центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ - ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$.
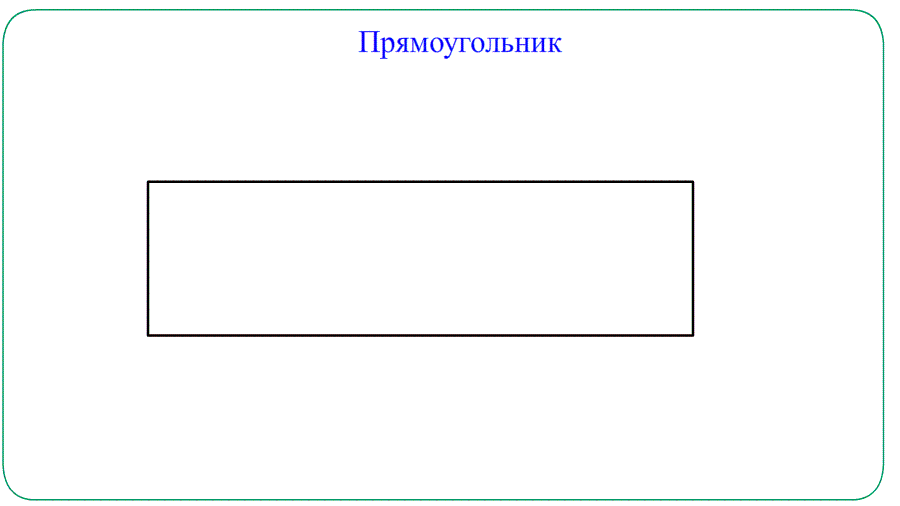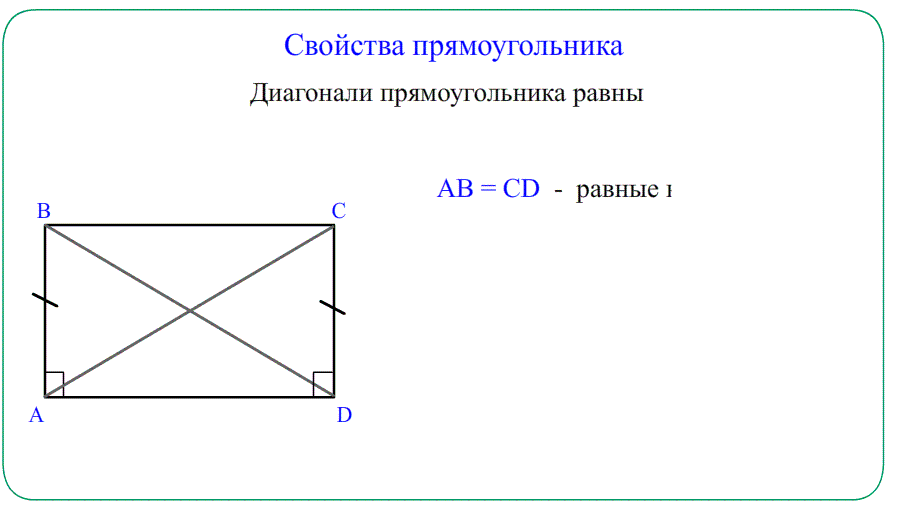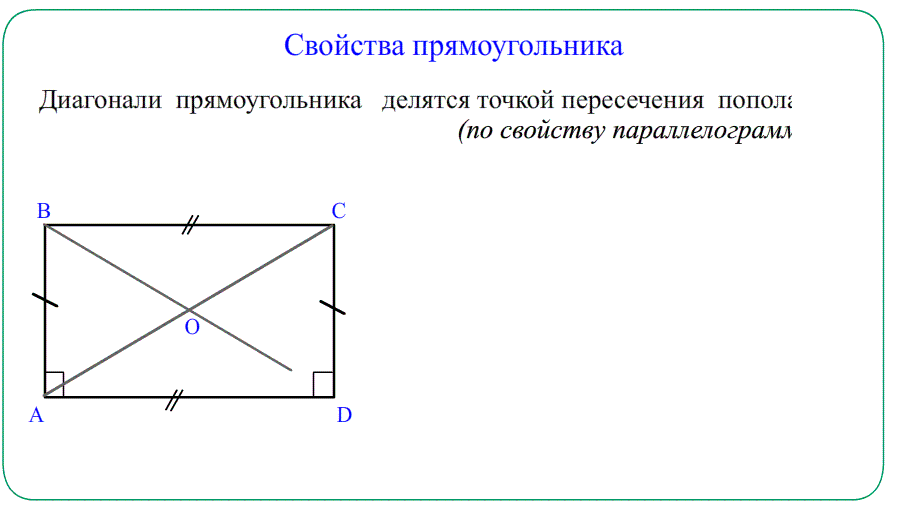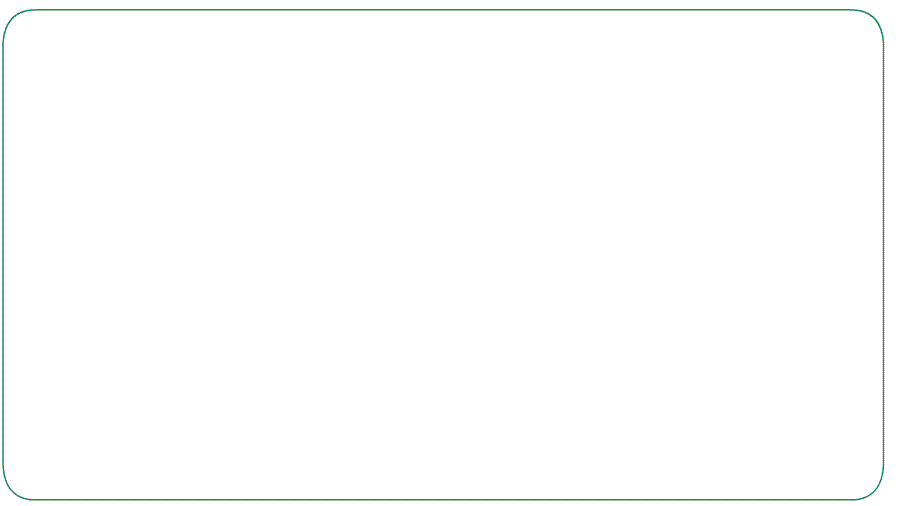
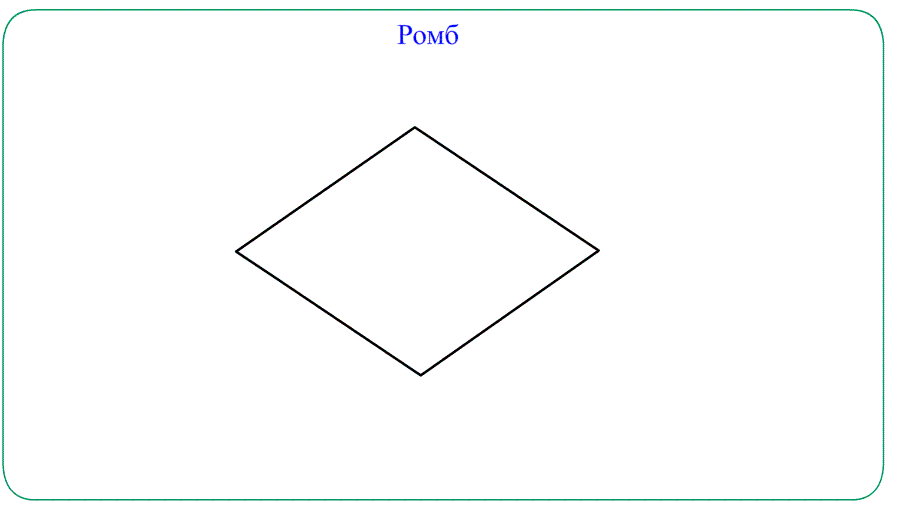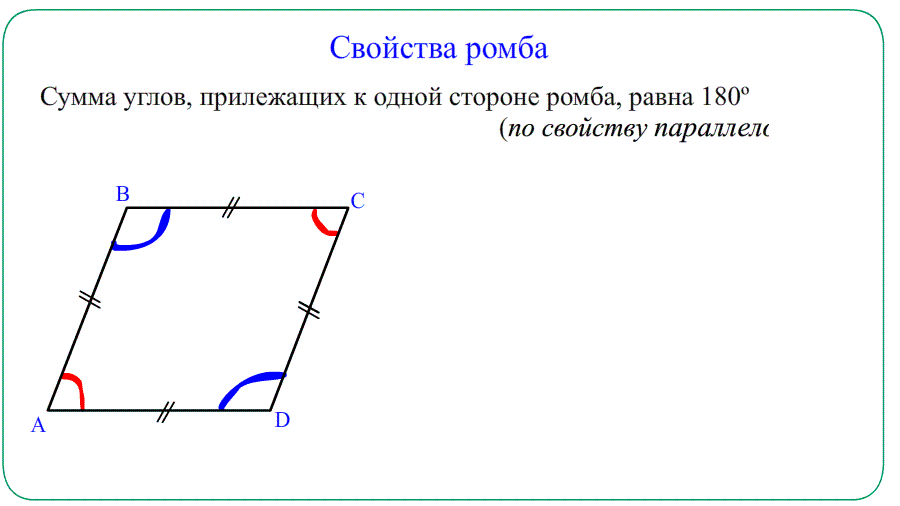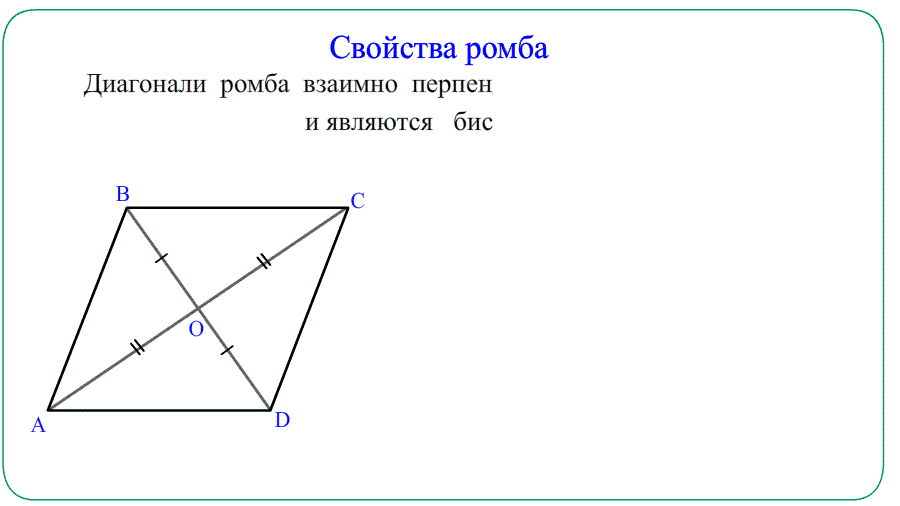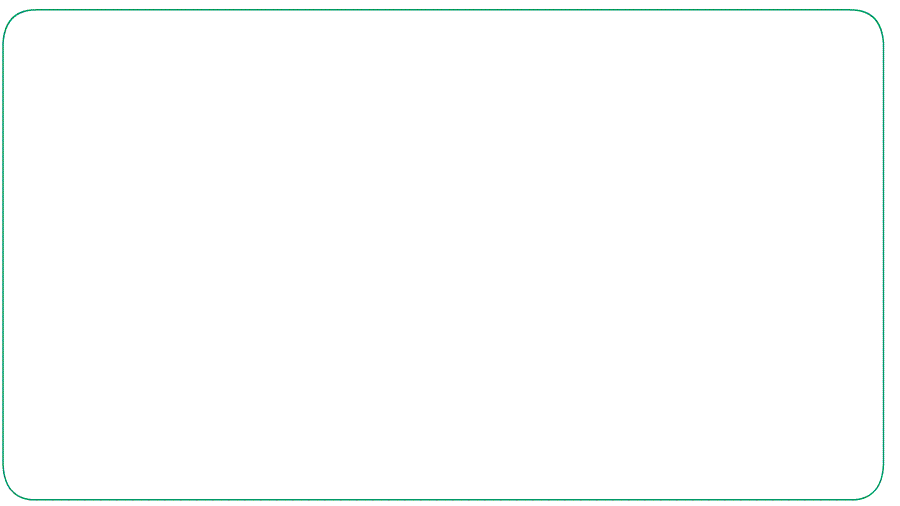
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов - делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2\cdot a\cdot b\cdot\cos D$ , большая - $BD^2=a^2+b^2+2\cdot a\cdot b\cdot\cos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4\cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=AD\cdot CH$ , $S=a\cdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2\cdot\sin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=\frac{AC\cdot BD}{2}$ . - половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если ... суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=p\cdot r$, $p=2\cdot a$ $S=2\cdot a \cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали - суть биссектрисы углов.
Задача 1: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: "Односторонние углы": В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30'$ , $67^o30'$
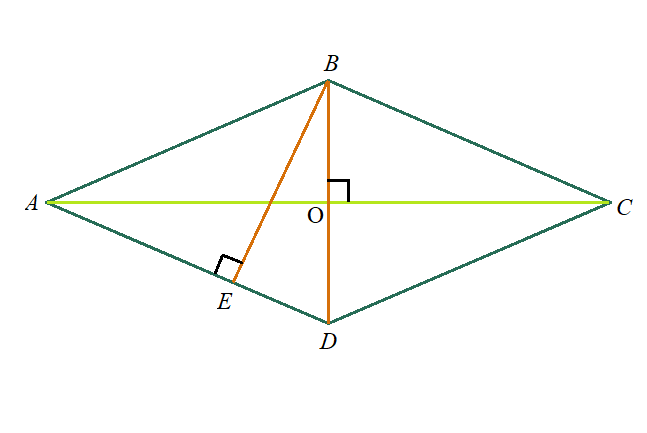
Задача 2: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $\bigtriangleup BED \sim \bigtriangleup AOD=\bigtriangleup AOB=\bigtriangleup COB=\bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $\alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $\alpha$ в $\bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $\Rightarrow$ $\sin\alpha=\frac{BE}{BD}=\frac{12}{13}$
- Перейдем к $\bigtriangleup OCD$ : в нем прилежащий катет $OD=\frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $\sin^2\alpha+\cos^2\alpha=1$ . Тогда косинус: $\cos\alpha=\pm\sqrt{1-\sin^2\alpha}=\pm\sqrt{1-\frac{144}{169}}=\pm\sqrt{\frac{25}{169}}=\pm\frac{5}{13}$
- Угол $\alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $\cos\alpha = \frac{5}{13}$
- Тогда: $\frac{DO}{DC}=\frac{6,5}{DC}=\cos\alpha=\frac{5}{13}$ $\Rightarrow$ $DC=\frac{6,5\cdot13}{5}=\frac{13\cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9\cdot12=202,8$
Задача 3: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ - пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
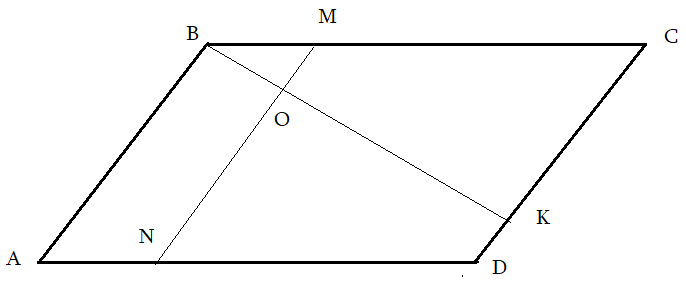
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ - параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ - квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $\Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб - это параллелограмм, у которого все стороны равны.
- "Чтоб Выучить, распознать нечто стоящее - узнать его в движении, при изменениях"
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей - ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали - новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали - ромб совпадает с самим собой. Симметрия.
Замечание: Если "зряче видим" центральную и осевые симметрии ромба, то все его свойства у нас "в кармане".
Свойства ромба:
- Ромб симметричен относительно точки O - пересечения диагоналей. O - центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ - ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов - делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2\cdot a\cdot b\cdot\cos D$ , большая - $BD^2=a^2+b^2+2\cdot a\cdot b\cdot\cos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4\cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=AD\cdot CH$ , $S=a\cdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2\cdot\sin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=\frac{AC\cdot BD}{2}$ . - половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если ... суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=p\cdot r$, $p=2\cdot a$ $S=2\cdot a \cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали - суть биссектрисы углов.
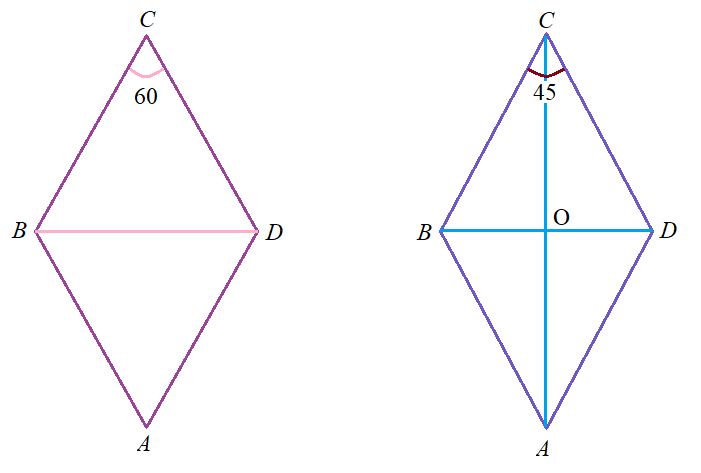
Задача 1: Найти периметр ромба $ABCD$, в котором $\angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $\bigtriangleup BCD$. Что в нём равного? $\Rightarrow$ каков данный треугольник?
- По условию, угол $\bigtriangleup BCD$ у вершине $\angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: "Односторонние углы": В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30'$ , $67^o30'$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $\bigtriangleup BED \sim \bigtriangleup AOD=\bigtriangleup AOB=\bigtriangleup COB=\bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $\alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $\alpha$ в $\bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $\Rightarrow$ $\sin\alpha=\frac{BE}{BD}=\frac{12}{13}$
- Перейдем к $\bigtriangleup OCD$ : в нем прилежащий катет $OD=\frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $\sin^2\alpha+\cos^2\alpha=1$ . Тогда косинус: $\cos\alpha=\pm\sqrt{1-\sin^2\alpha}=\pm\sqrt{1-\frac{144}{169}}=\pm\sqrt{\frac{25}{169}}=\pm\frac{5}{13}$
- Угол $\alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $\cos\alpha = \frac{5}{13}$
- Тогда: $\frac{DO}{DC}=\frac{6,5}{DC}=\cos\alpha=\frac{5}{13}$ $\Rightarrow$ $DC=\frac{6,5\cdot13}{5}=\frac{13\cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9\cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ - пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.

Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ - параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ - квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $\Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб - это параллелограмм, у которого все стороны равны.
- "Чтоб Выучить, распознать нечто неподвижное - узнать его в движении, при изменениях"
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей - ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали - новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали - ромб совпадает с самим собой. Симметрия.
Замечание: Если "зряче видим" центральную и осевые симметрии ромба, то все его свойства у нас "в кармане".
Свойства ромба:
- Ромб симметричен относительно точки O - пересечения диагоналей. O - центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ - ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов - делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Квадрат - одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $\angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $\bigtriangleup BCD$. Что в нём равного? $\Rightarrow$ каков данный треугольник?
- По условию, угол $\bigtriangleup BCD$ у вершины $\angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: "Односторонние углы": В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30'$ , $67^o30'$


- Полезные напоминания: "В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник - стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения (A):
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
