Пример 1: решить уравнение $2x^3+7x^2-10x-35=0$
- Решение: Группируем попарно и выносим за скобки общие множители:
- $2x^3+7x^2-10x-35=0$ $(2x^3+7x^2)-(10x+35)=0$ $x^2(2x+7)-5(2x+7)=0$
- $(2x+7)(x^2-5)=0$ . Основная цель - получить произведение равно нулю и решать отдельные случаи обнуления множителей.
- $2x+7=0$ $x^2-5=0$ Ответы: $x=-3,5$ $x=\sqrt{5}$ $x=-\sqrt{5}$
Пример 2: решить уравнение $x^4-x^3-9x^2-27=0$
- Решение: Группируем слагаемые: 1-ое и 3-е, 2-ое и 4-ое, выносим за скобки общие множители:
- $x^4-9x^2-x^3-27=0$ $x^2(x^2-9)-(x^3+27)=0$
- В первой скобке разложим разность квадратов, во второй сумму кубов $a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)$
- $x^2(x-3)(x+3)-(x+3)(x^2-3x+9)=0$ ... общий множитель, выносим .. $(x+3)(x^3-3x^2-x^2+3x-9)=0$
- $(x+3)(x^3-4x^2+3x-9)=0$ . цель: произведение равно нулю и решать обнуления множителей.
- $x+3=0$ $x^3-4x^2+3x-9=0$ Ответы: $x=-3$
Теорема Безу: если $x=c$ является корнем алгебраического уравнения $P\left(x\right)=0$, то многочлен $P\left(x\right)$ нацело делится на двучлен $x-c$. Т.е. разлагается на множители $P\left(x\right)=(x-c)(Q\left(x\right))$
Теорема Виета, следствие: "Хорошие", целые корни многочлена следует искать среди делителей свободного члена. Если старший коэффициент не равен 1, то среди всевозможных делений делителей свободного члена на делители старшего коэффициента.
Пример 3: решить уравнение $7x^3+2x^2-x-8=0$
- Решение: Легко угадаем, что $x=1$ - корень; подставим 1 и увидим выравнивание: $7\cdot1^3+2\cdot1^2-1-8=0$.
- Значит, Многочлен $7x^3+2x^2-x-8$ раскладывается на множители $\left(x-1\right)\left(?\right)$. Найдем разложение:
Разложение на множители: по-шаговый вынос за скобки простого множителя:
- Начнем $7x^3$ . Добавим или вычтем столько $?x^2$, чтоб при выносе за скобку общего множителя, оставался $(x-1)$.
- $7x^3-7x^2+7x^2+2x^2-x-8=0$ , вычли и добавили $7x^2$. Вынесем за скобку $x^2$, упростим $7x^2\left(x-1\right)+9x^2-x-8=0$ .
- Итак: вначале у нас уже выделен множитель $(x-1)$. Теперь надо проделать такое же с квадратом $9x^2$.
- Вычтем и добавим $9x$ : $7x^2\left(x-1\right)+9x^2-9x+9x-x-8=0$. Вынос: $7x^2\left(x-1\right)+9x\left(x-1\right)+8x-8=0$
- В последних двух слагаемых "обнаруживаем" желанное $(x-1)$ : $7x^2\left(x-1\right)+9x\left(x-1\right)+8\left(x-1\right)=0$
- Вот и все готово, чтоб вынести $(x-1)$ за скобки всего выражения: $\left(x-1\right)\left(7x^2+9x+8\right)=0$
- Было кубическое выражение, а теперь стало уравнение вида "произведение множителей = 0 ". Распад на случаи "множитель=0":
- Первый множитель: $x-1=0$ дает тот самый корень, что мы нашли "угадыванием": Ответ: $x=1$
- Второй множитель: $7x^2+9x+8=0$ , квадратное уравнение с $D=81-4\cdot7\cdot8<0$ , значит не имеет корней.
Схема Горнера: деление многочлена $7x^3+2x^2-x-8$ на $x-1$: корень $1$
1 | 7 2 -1 -8 $7x^3+2x^2-x-8$
__ | 7 9 8 =0 $7x^2+9x+8$
Пример 4: решить уравнение $2x^3+9x^2+13x+6=0$
Нахождение одного "хорошего" корня, угадывание 1-го решения:
- Решение: Как найти целый корень? Как угадать одно "хорошее" решение?
- Выпишем все множители свободного от $x$ члена, в нашем случае $6$: его множители $1$, $2$, $3$, $6$
- Также нужно найти множители старшего коэффициента $2$, т.е. множителя $x^3$: его множители $1$, $2$
- Раздедим все множители свободного $6$ на множители старшего $2$, получим список: $1$, $2$, $3$, $6$, $\frac{1}{2}$, $\frac{3}{2}$.
- Добавим в список все отрицательные значения: $1$, $2$, $3$, $6$, $\frac{1}{2}$, $\frac{3}{2}$, $-1$, $-2$, $-3$, $-6$, $-\frac{1}{2}$, $-\frac{3}{2}$.
- Корень кубического уравнения следует искать среди этих чисел: путем перебора и проверки на "выравнивание" уравнения.
- Подставим $x=-1$ и убедимся, что это верный корень: $2(-1)^3+9(-1)^2+13(-1)+6=-2+9-13+6=0$
Разложение на множители по формулам разности степеней:
- Формулы: $a^2-b^2=\left(a-b\right)\left(a+b\right)$ $a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)$ $a^4-b^4=\left(a-b\right)\left(a^3+a^2b+ab^2+b^3\right)$
- В уравнении: Вычтем из каждого слагаемого $2x^3+9x^2+13x+6$ их же значения при найденном ранее корне $x=-1$.
- $2x^3-2(-1)^3+9x^2-9(-1)^2+13x-13(-1)+6-6=0$ и разложим каждую полученную разность по формулам
- $2x^3-2(-1)^3=2(x^3-(-1)^3)=2(x+1)(x^2-x+1)$ $9x^2-9(-1)^2=9(x+1)(x-1)$ $13x-13(-1)=13(x+1)$
- $2(x+1)(x^2-x+1)+9(x+1)(x-1)+13(x+1)=0$ , Все готово к выносу общего множителя $x+1$ за скобки
- $(x+1)(2x^2-2x+2+9x-9+13)=0$ упростим, получим окончательное разложение $(x+1)(2x^2+7x+6)=0$
Продолжение решения уравнения: $(x+1)(2x^2+7x+6)=0$ - произведение множителей = 0. Распад на случаи!
- Второй множитель: $2x^2+7x+6=0$ , $D=49-48=1$ , два корня: $x=-1,5$ $x=-2$
- Первый множитель: $x+1=0$ дает найденный ранее корень. Ответы: $x=1$ $x=-1,5$ $x=-2$
Схема Горнера: деление многочлена $2x^3+9x^2+13x+6$ на $x+1$: корень $-1$
-1 | 2 9 13 6 $2x^3+9x^2+13x+6$
__ | 2 7 6 =0 $2x^2+7x+6$
Иллюстрации по схеме Горнера:
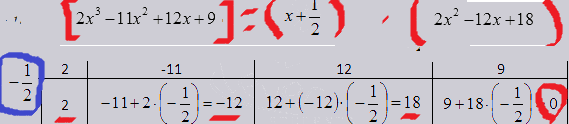

Пример 5: кубический многочлен $x^3+4x^2+3x-2$ поделить на $x+2$ по схеме Горнера.
-2 | 1 4 3 -2 $x^3+4x^2+3x-2$
__ | 1 2 -1 =0 $x^2+2x-1$
Пример 6: решить $x^4−3x^3−2x^2−3x+1=0$ - уравнение 4-ой степени
- Решение: $x=0$ не является корнем этого уравнения, поэтому можно обе части уравнения поделить на $x^2$.
- $x^2-3x-2-\frac{3}{x}+\frac{1}{x^2}=0$ $\left( x^2+\frac{1}{x^2} \right) - 3\left(x+\frac{1}{x}\right)-2=0$
- Замена $y=x+\displaystyle\frac{1}{x}$. Тогда $y^2=x^2+2+\displaystyle\frac{1}{x^2}$. Получим $y^2−3y−4=0$
- Решения $y=-1$ $y=4$ и "возврат" к $x$ неизвестному: $x+\frac{1}{x}=-1$ $x+\frac{1}{x}=4$
- $x^2+x+1=0$ - нет решений, $x^2-4x+1=0$ Ответы: $x=2-\sqrt{3}$, $x=2+\sqrt{3}$
Пример 7: решить $2x^4-11x^3-8x^2+59x+30=0$
- Ищем 1 корень: Свободный член $30$, его делители $1, 2, 3, 5, 6, 10, 15, 30$. Делители старшего коэффициента $1, 2$
- Список кандидатов на "хорошие" корни: $\pm1, \pm2, \pm3, \pm5, \pm6, \pm10, \pm15, \pm30, \pm\frac{1}{2}, \pm\frac{3}{2}, \pm\frac{5}{2}, \pm\frac{15}{2}$
- Поиск, перебор: $x=-2$: $2(-2)^4-11(-2)^3-8(-2)^2+59(-2)+30=32+88-32-118+30=0$
- Выносим $x+2$ за скобки: к 4-ой степени сделаем добавку $4x^3$: $2x^4+4x^3-15x^3-8x^2+59x+30=0$
- Из 1-го и 2-го слагаемого выносим общий множитель: $2x^3\left(x+2\right)-15x^3-8x^2+59x+30=0$
- Теперь, к кубу организуем "нужное" вычитание: $2x^3\left(x+2\right)-15x^3-30x^2+22x^2+59x+30=0$ ....
- ... и выносим общий множитель: $2x^3\left(x+2\right)-15x^2\left(x+2\right)+22x^2+59x+30=0$ . В скобках конечно же $x+2$
- Что прибавить к $22x^2$, чтоб в скобках "увидеть" $x+2$: $2x^3\left(x+2\right)-15x^2\left(x+2\right)+22x^2+44x+15x+30=0$
- В последних парах выносим общие: $2x^3\left(x+2\right)-15x^2\left(x+2\right)+22x\left(x+2\right)+15\left(x+2\right)=0$
- $\left(x+2\right)\left(2x^3-15x^2+22x+15\right)=0$ - итоговое разложение многочлена 4-ой степени на (линейное) * (куб)
- Решаем "произведение = 0 " через "распад на множители": $x+2=0$ $2x^3-15x^2+22x+15=0$ .
- Решаем кубическое $2x^3-15x^2+22x+15=0$ . Ищем, угадываем корень: найдем $x=3$ путем подбора.
- Разложим кубическое. Выносим $(x-3)$ за скобки: $2x^3-2\cdot 3^3-15x^2+15\cdot 3^2+22\cdot x-22\cdot 3=0$
- $2\left(x-3\right)\left(x^2+3x+9\right)-15\left(x-3\right)\left(x+3\right)+22\left(x-3\right)=0$
- $\left(x-3\right)\left(2x^2+6x+18-15x-45+22\right)=0$ $\left(x-3\right)\left(2x^2-9x-5\right)=0$
- $x-3=0$ $2x^2-9x-5=0$ $D=81+40$ $x=\frac{9+11}{4}$ $x=\frac{9-11}{4}$
- Ответы: $x=3$ $x=-2$ $x=5$ $x=-\frac{1}{2}$
Классная Интерактивная Доска:
Упражнения:
