Квадратное уравнение. Дискриминант
Каноническое квадратное уравнение
- Что такое обычное квадратное уравнение?
- Это уравнение, в котором обязательно есть икс в квадрате. Видов квадратных уравнений много. Но самый «главный» ...
стандартный или канонический вид : $a\cdot x^2+b\cdot x+c=0$ или $0=a\cdot x^2+b\cdot x+c$

Числа $a$ , $b$ , $c$ при неизвестном называются коэффициентами уравнения . У каждого свое название:
- $a$ называют квадратным (т.к. он при $x^2$) или первым коэффициентом ;
- $b$ называют линейным (т.к. он при $x$ ) или вторым коэффициентом ;
- $c$ называют свободным членом уравнения (т.к. он свободен от неизвестного)
- Важно правильно определять коэффициенты, ведь они участвуют в формулах решения квадратного уравнения!
- Особое внимание на знаки: в $a\cdot x^2+b\cdot x+c=0$ написаны одни "плюсы", а в вашем уравнении могут быть и "минусы" !
Определяем коэффициенты так:
$0,2x^2+7x+13=0$ коэффициенты : $a=0,2$ $b=7$ $c=13$
$3x^2-5x+10=0$ коэффициенты : $a=3$ $b=-5$ минус! $c=10$
$x^2-\frac{1}{3}x-5=0$ коэффициенты : $a=1$; $b=-\frac{1}{3}$ $c=-5$ минус!
$16x^2-25=0$ коэффициенты : $a=16$ $b=0$ $c=-25$ минус!
$-\frac{1}{6}x^2-\frac{2}{3}x=0$ коэффициенты : $a=-\frac{1}{6}$ $b=-\frac{2}{3}$ минус! $c=0$
Внимание: если дано нестандартное уравнение, чтобы не ошибиться в определении коэффициентов,сначала перепишите его в стандартном виде :
$49-36x^2=0$
$\Leftrightarrow $
$-36x^2+49=0$
$\Rightarrow $
$a=-36$ ; $b=0$ ; $c=49$
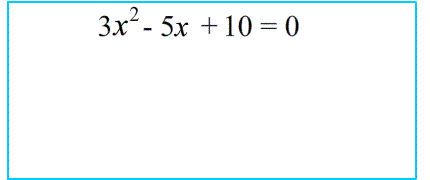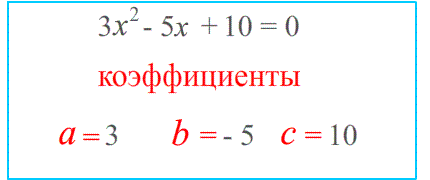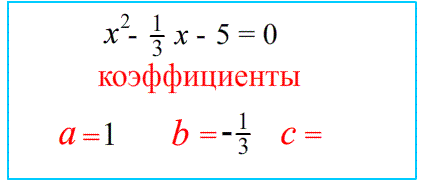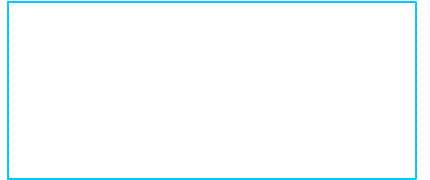

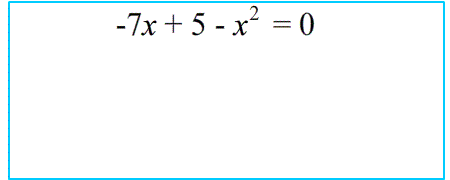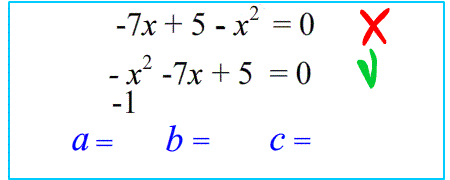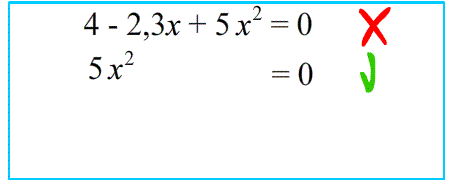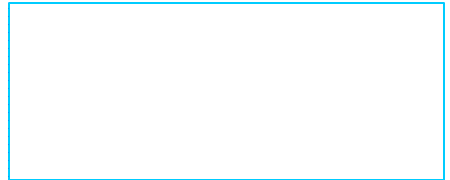
Формула решения канонического квадратного уравнения. Дискриминант
Канонический вид квадратного уравнения $ax^2+bx+c=0$ , $a$, $b$, $c$ - коэффициенты уравнения.
- Формула, составленная из трех коэффициентов уравнения $D=b^2-4ac$ называется Дискриминант .
- Дискриминант помогает ответить на вопрос "Есть ли у данного уравнения корни, сколько их ?" и решить его.
2) $D=0$ - да, уравнение нужно решать и у него будет один корень .
3) $D < 0$ - нет, при отрицательном дискриминанте нет корней и решать уравнение не стоит!
Формулы нахождения корней канонического квадратного уравнения:
2) "-" корень $x=\frac{-b-\sqrt{b^2-4ac}}{2a}$ или $x=\frac{-b-\sqrt{D}}{2a}$ .
Пример 1: $x^2-3x-4=0$
- Определяем коэффициенты уравнения: $a=1$ , $b=-3$ , $c=-4$
- Найдем Дискриминант и выясним, есть ли корни у этого уравнения.
- Внимание! Чтобы не ошибиться при подстановке отрицательного коэффициента в формулу, лучше заключить его в скобки:
- $D=b^2-4ac=\left(-3\right)^2-4\cdot 1\cdot\left(-4\right)=9+16=25$
- Т.к. $D=25 > 0$ , значит уравнение имеет два корня ,
- найдем корни по формулам : $x=\frac{-b+\sqrt{D}}{2a}=\frac{-\left(-3\right)+5}{2}=\frac{3+5}{2}=4$ и $x=\frac{-b-\sqrt{D}}{2a}=\frac{-\left(-3\right)-5}{2}=\frac{3-5}{2}=-1$
- Ответ: $x=4$ ; $x=-1$
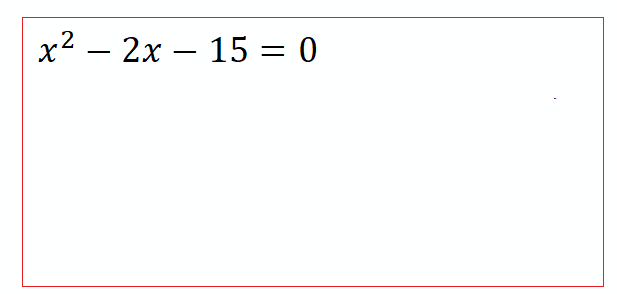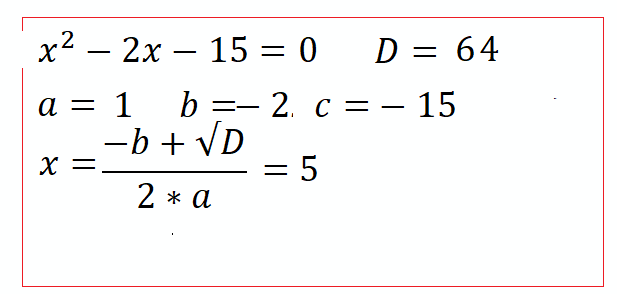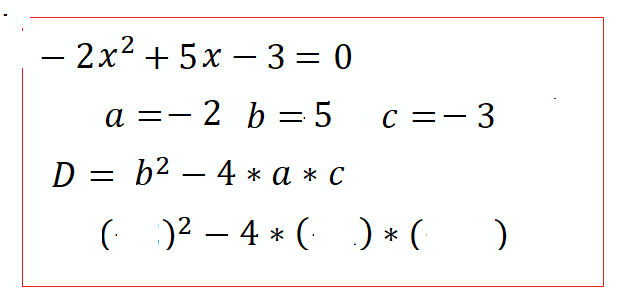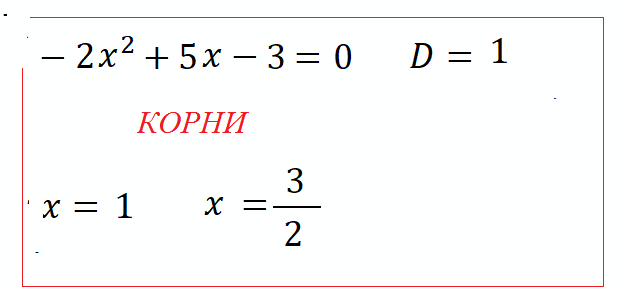


Замечание: Не всегда при извлечении корня из Дискриминанта получается целое число. В этом случае, решением уравнения будет дробное выражение с радикалом. Посмотрите внимательно, можно ли упростить полученное выражение ? Ответ должен быть всегда в сокращенном виде.
Пример 2: $7x^2-2x-7=0$
- Определяем коэффициенты уравнения: $a=7$ , $b=-2$ , $c=-7$
- $D=b^2-4ac=\left(-2\right)^2-4\cdot7\cdot\left(-7\right)=4+196=200.$ Т.к. $D=200 > 0$ , значит уравнение имеет два корня :
- Внимание! Окончательный ответ нужно давать всегда в сокращенном виде.
- 1) $x=\frac{-b+\sqrt{D}}{2a}=\frac{2+\sqrt{200}}{2\cdot7}$ в таком виде корень оставлять нельзя, т.к. дробь еще можно сократить:
- из-под корня можно вынести множитель 10, после возможно сокращение: $x=\frac{2+\sqrt{200}}{2\cdot7}=\frac{2+10\sqrt{2}}{2\cdot7}=\frac{1+5\sqrt{2}}{7}$;
- 2) $x=\frac{-b-\sqrt{D}}{2a}=\frac{1-5\sqrt{2}}{7}$ Ответ: $x=\frac{1+5\sqrt{2}}{7}$ ; $x=\frac{1-5\sqrt{2}}{7}$
Интерактивная Доска:
Упражнения:
Послесловие
Если скорость Ваших исполнений низкая, часто допускаете ошибки, пройдите Тест-упражнение несколько раз,
для этого откройте Тест-Упражнение через "Решать заново":
Наведите курсор на это упражнение и выберите этот пункт меню .
Тест-Упражнение откроется с новыми аналогичными примерами и вы получите "новое" задание.
Решение Уравнений Методом Разложения на Множители
Уравнение - это равенство двух выражений с неизвестной переменной.
Решить уравнение - значит найти те числа, которые вместо иксов уравнивают два выражения .
- Как находить решения уравнения? Посмотреть: какие числа надо поставить вместо иксов, чтоб после вычислений оба сравнялись.
- Подумать: нет ли еще каких-то чисел, которые могут уравнять обе части уравнения? Надо находить все такие!
- Если напрямую не удается найти такие числа, то как можно "переделать" уравнение в такой вид, чтоб можно было "угадать" решения.
- Такие способы "переделок" называются эквивалентными преобразованиями. Цепочка эквивалентных называется шагами решения.
- Эквивалентным шагом является перенос слагаемого из одной части в другую с заменой знака на противоположный.
- Также эквивалентен перенос множителя из одной в другую "как деление". Число, которое уравнивало" - также будет уравнивать!
- Еще: замена одного выражения на другое, ему тождественно равное . Например: открытие скобки, применение формулы .
Пример 1: Решить уравнение $(x+4)\cdot\left(5-3x\right)=0$
- Произведение $(x+4)\cdot\left(5-3x\right)$ равно 0 лишь тогда, когда какая-либо скобка станет 0, "обнулится".
- Как найти х - числа такие, чтоб произошло нужное обнуление? Надо решить два простых уравнения:
- $x+4=0$ перенесем слагаемое 4 вправо, поменяв знак $x=-4$
- $5-3x=0$ перенесем слагаемое $3x=5$ перенесем множитель 3 делением $x=\frac{5}{3}$
- При х - числах $x=-4$ и $x=\frac{5}{3}$ произведение $(x+4)\cdot\left(5-3x\right)$ становится нулём!
- ответ: $x=-4$ $x=\frac{5}{3}$
Пример 2: Решить уравнение $(8-x)\cdot\left(2x+7\right)=0$
решением уравнения являются те числовые значения $x$, при которых обе части уравнения выравниваются.
каким может быть $x$ , чтобы произведение скобок равнялось нулю? Одна из них 0? иначе никак.
Опорный факт: Если произведение $A\cdot B \cdot C$ = $0$ тогда либо $A$, либо $B$, либо $C$ = $0$
Правило: уравнение " произведение = $0$ " разбивается на случаи: каждый множитель = $0$
Разбиение на 2 случая: приравняем содержимое каждой скобки к нулю. и, решаем каждое уравнение по отдельности.
случай 1 $8-x=0$ $\Leftrightarrow$ $x=8$
случай 2 $2x+7=0$ $\Leftrightarrow$ $2x=-7$ $\Leftrightarrow$ $x=-3.5$
ответ: $x_1=8$ $x_2=-3.5$
Способ разбиения уравнения, разложения на множители:
- шаг 1: Обнулить правую часть уравнения, перенести все слагаемые влево. "левая часть = $0$".
- шаг 2: Разложить, вынести множители за скобки, превратить левую часть в произведение. " = $0$".
- шаг 3, 4 ... : Рассмотреть случаи: для каждого составить уравнения "множитель = $0$".
- далее: Решать получившиеся более мелкие уравнения. ответ: собрать все полученные решения..
Решение квадратного уравнения разложением, вынесением за скобку
Уравнение вида $ax^2+bx=0$: решается вынесением общего множителя $x$ за скобку.
После вынесения уравнение $x\cdot\left(ax+b\right)=0$ распадается на два уравнения, 2 случаи.
Уравнение вида $ax^2=cx$: решается переносом $cx$ влево и вынесением общего множителя.
После приведения к виду $ax^2-cx=0$ выносим множитель $x$ за скобки и решаем 2 случая.
Пример 3: Решить уравнение $6x^2–2x=0$ ;
-
вынесем общий множитель за скобки: $2x\cdot(3x – 1)=0$ ; распад на два случая:
-
$2x=0$ $\Rightarrow$ корень $x=0$ ;
-
$3x–1=0$ перенесем 1 вправо, поделим на 3. $\Rightarrow$ корень $x=\frac{1}{3}$
-
ответ: соберем все решения: $x_1=0$ ; $x_2=\frac{1}{3}$
Пример 4: Решить уравнение $50x^2-7x=0$
-
вынесем общий множитель $x$ за скобку, получаем $x\cdot\left(50x-7\right)=0$.
-
уравнение распадается на два случая. Каждый множитель приравниваем к $0$.
-
1-й: $x=0$ ; 2-й: $50x-7=0$ решаем и получаем $x=\frac{7}{50}$
-
ответ: $x_1=0$ $x_2=0.14$
Пример 5: Решить уравнение $4x^2=10x$
- Через сокращение $x$ решать это уравнение нельзя, т.к. потеряется корень $x=0$.
- Правильное решение - перенести всё в одну часть, затем вынести неизвестное за скобку

Уравнение вида $(ax)^2=c^2$: решается применением формули разности квадратОВ.
После переноса и разложения по формуле приведится к виду $(ax-c)(ax+c)=0$ . Далее решаем 2 случая.
Пример 6: Решить уравнение $9x^2-16=0$
- Разложим $9x^2-16$ на множители по формуле "разность квадратОВ".
- $(3x-4)\cdot\left(3x+4\right)=0$
- Произведение двух скобок равно нулю. Значит, два случая - каждую скобку приравняем к нулю:
- $3x-4=0$ перенос слагаемого $3x=4$ перенос множителя, решение: $x=\frac{4}{3}$
- $3x+4=0$ перенос слагаемого $3x=-4$ перенос множителя, решение: $x=-\frac{4}{3}$
- ответ: $x=\frac{4}{3}$ $x=-\frac{4}{3}$
Пример 7: Решить уравнение $(3-x)\cdot\left(4x+6x^2\right)\cdot\left(x^2-1\right)=0$
- Произведение скобок равно нулю. Для каждого множителя напишем уравнение "обнуления" и решим каждое.
- Каждое такое уравнение "скобка = 0" пишем в отдельной строке и решаем по - шагово.
-
Соберем ответы со всех уравнений: они появились на шагах №2, №6, №10, №14, №16.
-
№1 $3-x=0$
-
№2 $x=3$
-
№3 $4x+6x^2=0$
- №4 $2x(2x+3)=0$
- №5 $2x=0$
- №6 $x=0$
- №7 $2x+3=0$
- №8 $2x=-3$
- №9 $x=-\frac{3}{2}$
- №10 $x=-1,5$
- №11 $x^2-1=0$
- №12 $(x-1)(x+1)=0$
- №13 $x-1=0$
- №14 $x=1$
- №15 $x+1=0$
- №16 $x=-1$
- ответ: $x=3$ $x=0$ $x=-1,5$ $x=-1$ $x=1$


Классная Интерактивная Доска:
Упражнения:

ЕГЭ: Как сэкономить 30 мин на ЕГЭ и время при подготовке: Квадратные Уравнения
Квадратное уравнение, решение через Дискриминант
1. Путем упрощений (скобки, группирования) уравнение приведем к стандартному виду.
2. Стандартный, Канонический вид $ax^2+bx+c=0$ и $a,b,c-$коэффициенты уравнения.
3. Находим Дискриминант $D=b^2-4ac$ . Если $D < 0$ - нет корней !
$D > 0$ - два корня. $x=\frac{-b+\sqrt{D}}{2a}$ ; $x=\frac{-b-\sqrt{D}}{2a}$ . $D=0$ - один корень .
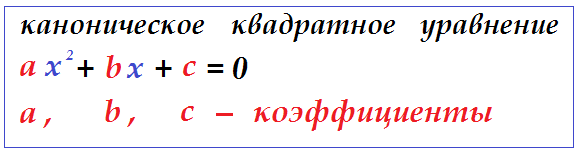

$0,2x^2+7x+13=0$ коэффициенты : $a=0,2$; $b=7$ ; $c=13$
$3x^2-5x+10=0$ коэффициенты : $a=3$ ; Внимание: $b=-5$ минус! ; $c=10$
$x^2-\frac{1}{3}x-5=0$ коэффициенты : $a=1$ ; Внимание: $b=-\frac{1}{3}$ и $c=-5$ минус! ;
$16x^2-25=0$ коэффициенты : $a=16$ ; $b=0$ ; $c=-25$ минус!
$-\frac{1}{6}x^2-\frac{2}{3}x=0$ коэффициенты : $a=-\frac{1}{6}$ ; $b=-\frac{2}{3}$ минус! ; $c=0$
Пример 1: $x^2-3x-4=0$ $a=1$ , $b=-3$ , $c=-4$
$D=b^2-4ac=\left(-3\right)^2-4\cdot1\cdot\left(-4\right)=9+16=25$. Дискриминант $D=25 > 0$ , два корня ,
$x=\frac{-b+\sqrt{D}}{2a}=\frac{-\left(-3\right)+5}{2}=\frac{3+5}{2}=4$ и $x=\frac{-b-\sqrt{D}}{2a}=\frac{-\left(-3\right)-5}{2}=\frac{3-5}{2}=-1$ Ответ: $x=4$, $x=-1$
Пример 2: $7x^2-2x-7=0$ $a=7$ , $b=-2$ , $c=-7$
$D=b^2-4ac=\left(-2\right)^2-4\cdot7\cdot\left(-7\right)=4+196=200$. Т.к. $D=200 > 0$ , имеет два корня :
$x=\frac{-b+\sqrt{D}}{2a}=\frac{2+\sqrt{200}}{2\cdot7}$ нужно сократить: $x=\frac{2+\sqrt{200}}{2\cdot7}=\frac{2+10\sqrt{2}}{2\cdot7}=\frac{1+5\sqrt{2}}{7}$ , второй $x=\frac{1-5\sqrt{2}}{7}$
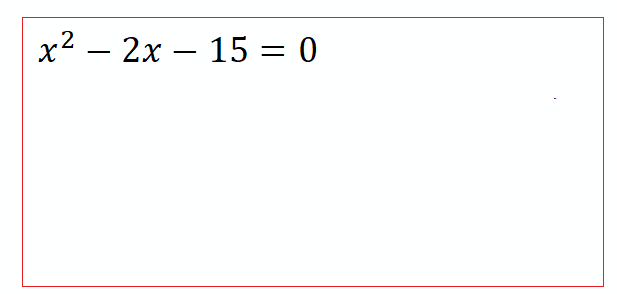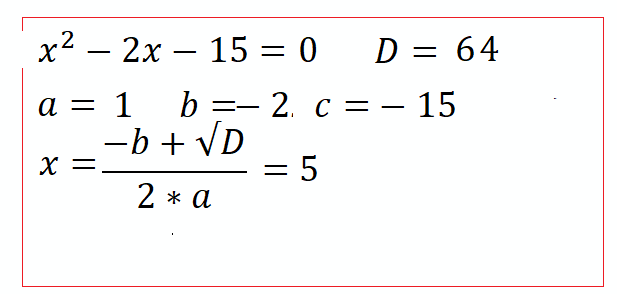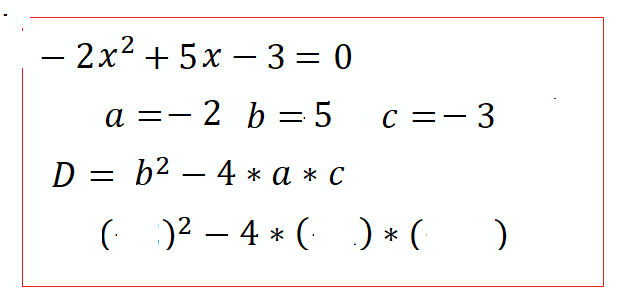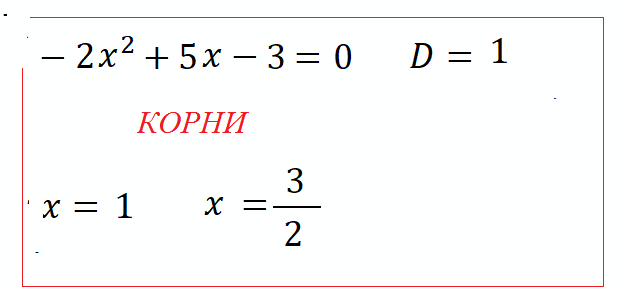

Неполное Квадратное уравнение, прямое решение
Квадратное уравнение, в котором $b$ или $c$ равен $0$ или оба сразу равны $0$ называется неполным.
Такие уравнения надо решать напрямую, без дискриминанта, практически наизусть!
Пример 3: уравнение вида "квадрат икс = число" : $x^2=c$
(1) $x^2=16$ Квадрат какого числа будет равен $16$? $x=4$ , $x=-4$.
(2) $x^2=289$ нужно найти чей квадрат 289 , "+" и "-" решения: $\pm\sqrt{289}=\pm17$ .
(3) $x^2=\frac{64}{121}$ чей квадрат $\frac{64}{121}$ ? $\Rightarrow$ ответ : $x=\frac{8}{11}$ ; $x=-\frac{8}{11}$.
(4) $x^2=13$ ответ : $x=\sqrt{13}$ ; $x=-\sqrt{13}$. Ну и что, что числа имеет радикальные?
(5) $x^2=-9$ не имеет корней, т.к. квадрат числа может быть только положительным!
Пример 4: Неполное $ax^2+c=0$ решается переносом слагаемого, затем множителя.
(1) $3x^2-75=0$ переносы: $3x^2=75$ $x^2=\frac{75}{3}$ $x^2=25$ $x=5$, $x=-5$
(2) $100x^2-49=0$ перенесем с $100x^2=49$ $x^2=0,49$, $x=0,7$, $x=-0,7$ .
Пример 5: Без свободного коэффициента: Уравнение вида $ax^2+bx=0$
решается вынесением $x$ за скобку. Произведение = 0 распадается на случаи.
$50x^2-7x=0$ вынесем общий множитель "х" за скобку $x\cdot\left(50x-7\right)=0$
Умножение двух равно 0 распадается на два случая, каждый множитель = 0 :
1) $x=0$ 2) $50x-7=0$ $x=\frac{7}{50}$ Ответ: $x=0$ ; $x=0.14$
Уравнение вида $ax^2=bx$ решается переносом $bx$ влево. (....не сокрашать!)
После приведения к виду $ax^2-bx=0$ , решается вынесением общего множителя "х" за скобки.
Определение: Решение уравнения - это число (или числа), выравнивающие обе части.
Пример 6: 1) $\left(x-3\right)^2=16$ Какое число в квадрате нам дает $16$? $\Leftrightarrow$ это$4$ и $-4$,
$x-3=4$ и $x-3=-4$; на два случая: $x-3=4$, $x-3=-4$ Ответ: $x=7$ ; $x=-1$
2) $\left(x-3\right)^2=289$ .... $x-3=\sqrt{289}$ $x-3=+17$,$x-3=-17$ Ответ: $x=20$ $x=-14$
(3) $x^2=144$ , $x=12$ и $x=-12$ (4) $\left(x+2\right)^2=81$ $x=-11$ и $x=7$
(5) $\left(x+5\right)\cdot\left(2x-9\right)=0$ $x=-5$ и $x=4.5$ (6) $2x^2+15=0$ нет решений!
Разложение квадратного на множители, угадывание корней, Виета
Иллюстрационный пример: $\left(x-3\right)\left(x+7\right)=0$ Какие корни? $x=3$ и $x=-7$
"каждый множитель может стать нулем". Теперь, изменим форму нашего уравнения на его канонический вид:
Как образуются коэффициенты? $x^2+7x-3x-3\cdot7=0$ ... $x^2-\left(3-7\right)\cdot x+\left(-3\cdot7\right)=0$
$x^2+4\cdot x-21=0$ его корни те же: $D=100$ $x_1=\frac{-4+10}{2}=3$ $x_2=\frac{-4-10}{2}=-7$
Как связаны сумма и произведение корней квадратного уравнения $x^2+4\cdot x-21=0$ с его коэффициентами?
сумма корней $x_1+x_2=3+\left(-7\right)=-4$ (=$-\frac{b}{a}$) , произведение корней $x_1\cdot x_2=3\cdot\left(-7\right)=-21$ (=$\frac{c}{a}$)
Пример 7: разложить на множители 1. $x^2-10x-39=\left(x-?\right)\left(x+?\right)$ что там? $=\left(x-3\right)\left(x+13\right)$ !
2. $2x^2-3x-5=\left(2x-?\right)\left(x-?\right)=\left(2x+1\right)\left(x-5\right)=2\left(x+\frac{1}{2}\right)\left(x-5\right)$ - можно было угадать ?=-1 ?=5
3. $-3x^2+7x+10=-3\cdot\left(x+1\right)\cdot\left(x-\frac{10}{3}\right)$ если еще упростить, то $=\left(x+1\right)\left(10-3x\right)$
Теорема Виета: для квадратного $ax^2+bx+c=0$ уравнения
$x_1+x_2=-\frac{b}{a}$ - сумма корней равна "минус 2-ой коэффициент разделить на 1-ый"
$x_1\cdot x_2=\frac{c}{a}$ - произведение корней равно "свободный член разделить на 1-ый".
Теорема Виета о разложении на множители : $ax^2+bx+c=a\cdot\left(x-x_1\right)\cdot\left(x-x_2\right)$
Как разложить квадратное выражение на линейные множители :
1. Угадать, что должно быть внутри скобки $\left(ax-?\right)\left(x-?\right)$ --- перебирать множители, делители.
2. Найти корни через дискриминант и собрать скобки по формуле Виета.
3. Замечание: если целые корни, то они всяко будут делителями свободного. Их то немного!



Пример 8: $x^2+2\cdot x-63=0$ $\Leftrightarrow$
по теореме Виета произведение корней равно $-63$ . какими могуть быть корни, чтоб произведение стало $-63$ ?
если корни "хорошие, не радикальные" числа, то они должны быть делителями свободного члена $-63$ .
значит, надо искать среди $\pm1,\pm3,\pm7,\pm9,\pm21,\pm63$ . по теореме Виета сумма корней равна $-2$ .
очевидно, такая пара среди делителей $7$ и $-9$ . Нам надо было "угадать" пару чисел, $x=7$ $x=-9$,
Пример 9: Решение уравнений наизусть с помощью "Виета"
1. $x^2+4\cdot x-21=0$ $\Leftrightarrow$ корни $x=3$ и $x=-7$ являются делителями числа 21.
2. $x^2+2\cdot x-63=0$ $\Leftrightarrow$ корни $x=7$ и $x=-9$, каждый из них делят число 63.
3. $x^2+10x-39=0$ $\Leftrightarrow$ корни $x=13$ и $x=-3$ среди делителей числа 39.
4. $y^2+y-12=0$ , найти корни уравнения. все делители свободного члена $\pm1,\pm2,\pm3,\pm4,\pm6,\pm12$.
Надо найти два числа таких, чтобы произведение давало $+12$, а сумма $-1$. Перебрать разные пары и
докопаться до двух чисел $3$ и $-4$ с нужными свойствами "Виета". Они и есть корни!
По коэффициентам квадратного уравнения, не решая его, можно узнать сумму корней и произведение корней.
Зная сумму корней и произведение корней, можно "восстановить" квадратное уравнение с этими корнями.
Пример 10: 1. составить квадратное уравнение с корнями $-\frac{1}{2}$ и $4$ .
по обратной теореме Виета, его линейным, при $x$, коэффициентом должен быть $-\left(-\frac{1}{2}+4\right)$ ,
а свободным членом будет произведение $\left(-\frac{1}{2}\right)\cdot4$ . Уравнение $x^2-\frac{7}{2}\cdot x-2=0$ .
2. Найти параметр $c$ уравнения $x^2+10x-c=0$ если известен один из корней $x=13$ .
по теореме Виета, сумма корней $x_1+x_2=-10$ . Раз один корень $x=13$ , значит, другой $x=-3$ .
но, тогда произведение корней диктует $-c=\left(13\right)\cdot\left(-3\right)$ , значит $c=39$ . А уравнение: $x^2+10x-39$ .
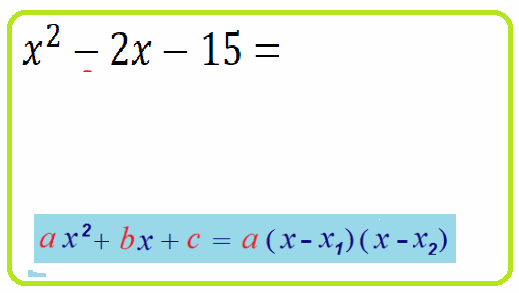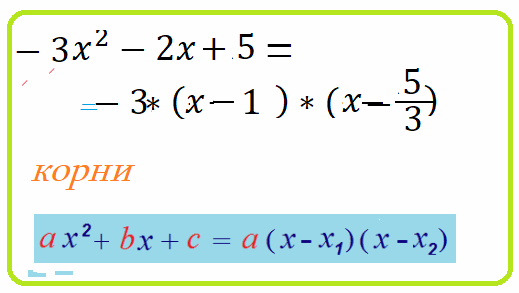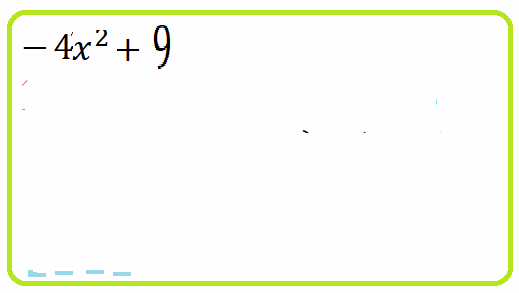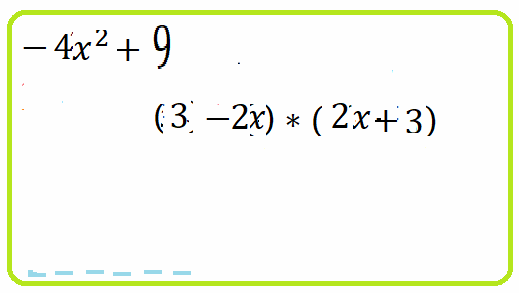
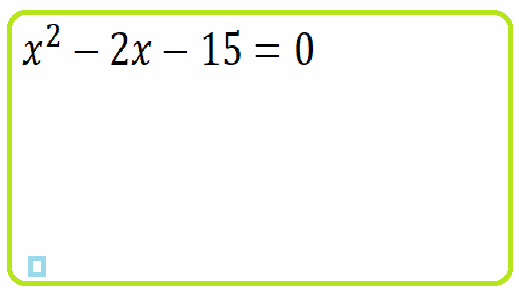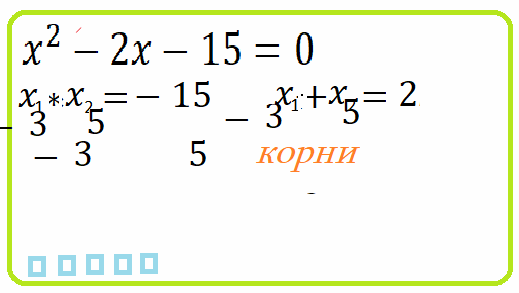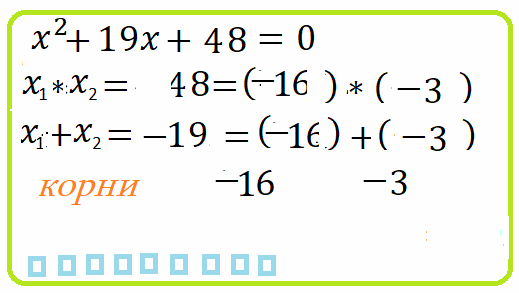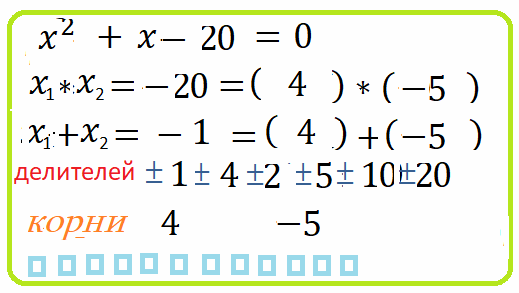

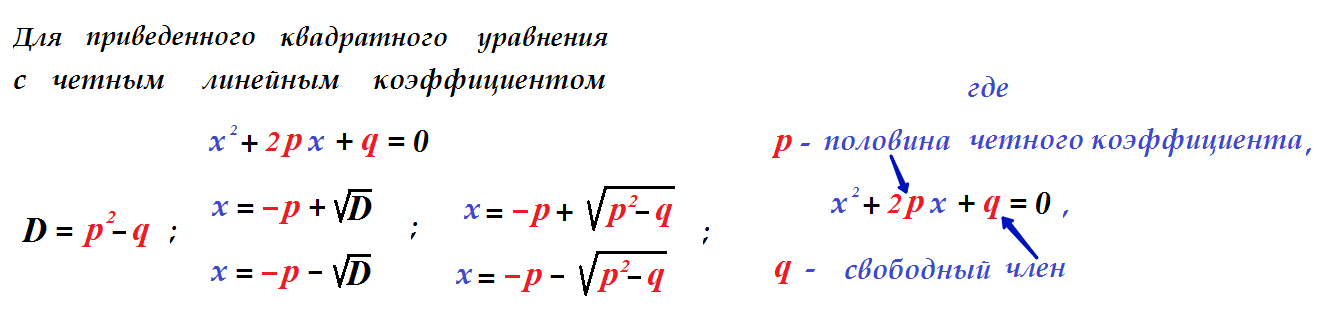
Обратите внимание в формуле Дискриминанта нет умножения на 4 !


Помните, упрощенные $D=p^2-q$ ; $x=-p+\sqrt{D}$ ; $x=-p-\sqrt{D}$
или $x=-p+\sqrt{p^2-q}$ ; $x=-p-\sqrt{p^2-q}$ можно применять только
для приведенных квадратных уравнений с четным линейным коэффициентом.
Пример 11: $x^2-8x+26=0$ $\Leftrightarrow$
$b=2p=-8$ $p=-4$ ; $q=26$
$D=p^2-q=\left(-4\right)^2-26=16-26=-10 < 0$ $\Rightarrow$ корней нет!
Как быть, если в уравнении перед $x^2$ стоит "-"?
Пример 12: $-x^2+8x-3=0$
это уравнение не является приведенным , т.к. первый коэффициент $=-1$ т.е. $\ne1$,
и упрощенные формулы применять нельзя, но легко .... умножить все уравнение на "-1"
$x^2-8x+3=0$ ф-лы : $D=\left(-4\right)^2-3=13$, $x=4+\sqrt{13}$ , $x=4-\sqrt{13}$
![]()
![]() .
.

Задание:
