Функция $y=\frac{k}{x}$ . Гипербола. Свойства.
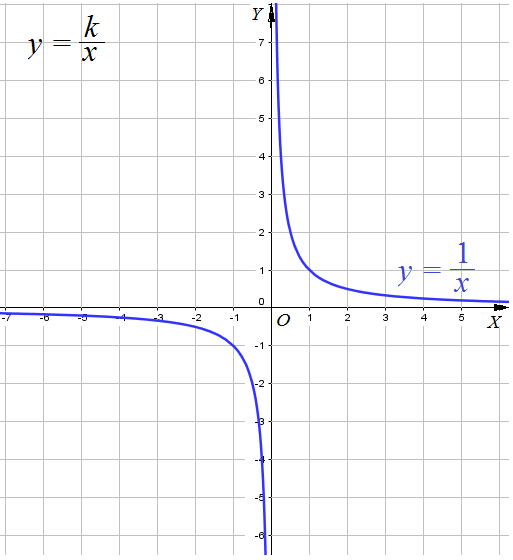
Пример 1: Построить график для функции $y=\frac{1}{x}$, $f\left(x\right)=\frac{1}{x}$
- Вычислим значения функции в разнознаковых точках и нанесем точки с вычисленными координатами в системе $XOY$.
- $x=1$ $f\left(1\right)=1$ $x=\frac{1}{2}$ $f\left(\frac{1}{2}\right)=2$ $x=-1$ $f\left(-1\right)=-1$ $x=-\frac{1}{2}$ $f\left(-\frac{1}{2}\right)=-2$
- $x=2$ $f\left(2\right)=\frac{1}{2}$ $x=\frac{1}{4}$ $f\left(\frac{1}{4}\right)=4$ $x=-2$ $f\left(-2\right)=-\frac{1}{2}$ $x=-\frac{1}{4}$ $f\left(-\frac{1}{4}\right)=-4$
- $x=4$ $f\left(4\right)=\frac{1}{4}$ $x=\frac{1}{8}$ $f\left(1\right)=8$ $x=-4$ $f\left(-4\right)=-\frac{1}{4}$ $x=-\frac{1}{8}$ $f\left(-\frac{1}{8}\right)=-8$ .
- В системе координат укажем точки $(1;1)$, $(2;1/2)$, $(4;1/4)$, $(1/2;2)$, $(1/4;4)$, $(1/8;8)$, $(-1;-1)$, $(-2;-1/2)$,
- Еще точки: $(-4;-1/4)$, $(-1/2;-2)$, $(-1/4;-4)$, $(-1/8;-8)$ . По всем точкам построим кривые - график функции $y=\frac{1}{x}$
- Функция $y=\frac{1}{x}$ не вычисляется при $x=0$, О.Д.З. $x\ne0$ . График имеет разрыв по вертикальной линии $x=0$. Ветви "прижаты" к ней.
- Ветви графика прижимаются к горизонтальной линии $y=0$. Функция $y=\frac{1}{x}$ ни при каких $x$ не принимает значение $y=0$
Графиком функции $y=\frac{k}{x}$ $k\ne0$ является гипербола , ветви прижимаются к асимптотическим линиям.
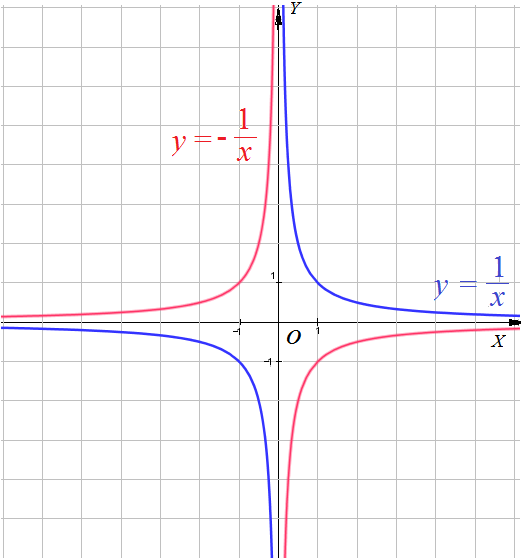
- если коэффициент $k > 0$ , в I и III координатных четвертях. Точка $(0;0)$ - центр симметрии.
- если $k < 0$ , то во II и IV координатных четвертях. Точка $(0;0)$ - центр симметрии.
- Асимптоты: Вертикальная асимптота, линия $x=0$, Горизонтальная асимптота, линия $y=0$
Cвойства функции $y=\frac{k}{x}$ при $k > 0$ ( ветви гиперболы расположены в первом и третьем координатных углах) .
- Свойство 1: Область Определения Функции - вся числовая прямая , кроме $x=0$.
- Свойство 2: $y > 0$ при $x > 0$; $y < 0$ при $x < 0$.
- Свойство 3: Функция убывает на промежутках $( - ∞ ; 0 )$ и $( 0 ; + ∞)$
- Свойство 4: Функция не ограничена ни снизу, ни сверху.
- Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
- Свойство 6: Функция непрерывна на $( - ∞ ; 0 )$ и $( 0 ; + ∞)$.
- Свойство 7: Область значений функции - $( - ∞ ; 0 )$ U $( 0 ; + ∞)$. имеет разрыв в точке $x=0$.
Cвойства функции $y=\frac{k}{x}$ при $k < 0$ (ветви гиперболы расположены во втором и четвертом координатных углах).
- Свойство 1: Область Определения Функции - вся числовая прямая , кроме $x=0$.
- Свойство 2: $y > 0$ при $x < 0$ ; $y < 0$ при $x > 0$.
- Свойство 3: Функция возврастает на промежутках $( - ∞ ; 0 )$ и $( 0 ; + ∞)$
- Свойство 4: Функция не ограничена ни снизу, ни сверху.
- Свойство 5: Ни наименьшего, ни наибольшего значений $у$ функций нет.
- Свойство 6: Функция непрерывна на $( - ∞ ; 0 )$ и $( 0 ; + ∞)$
- Свойство 7: Область значений функции - объединение $( - ∞ ; 0 )$ U $( 0 ; + ∞)$ . имеет разрыв в точке $x=0$.
Метод Замены для построения Графика Функции.
Мысль: Умеем строить график функции по-проще ... используем его для построения функции при "сдвинутых" аргументах и значениях.
Как построить график функции $y=k\cdot f\left(x\right)$, если известен график функции $y=f\left(x\right)$.
- График $y=5\cdot f\left(x\right)$: Растянуть вертикально вверх по оси $OY$ 5 раз все, что над $OX$ графика $y=f\left(x\right)$ , $k$ раза.
- График $y=5\cdot f\left(x\right)$: Расстянуть вертикально вниз по оси $OY$ 5 раз все, что под $OX$ графика $y=f\left(x\right)$ , $k$ раза.
- График $y=\frac{1}{3}\cdot f\left(x\right)$: Сжать по вертикали, оси $OY$ график $y=f\left(x\right)$ 3 раза.
- Еще способ: Перемасштабирование. Для $y=5\cdot f\left(x\right)$ ... построить $y=f\left(x\right)$, изменить масштаб: "1" станет "5", "-2" станет "-10", и т.д.
Как построить график функции $y=-f\left(x\right)$, если известен график функции $y=f\left(x\right)$.
- Эти функции принимают ровно противоположные значения. Значит: график $y=f\left(x\right)$ надо отразить по оси $OX$, "перевернуть".
Как построить график функции $y=f\left(x+l\right)$, если известен график функции $y=f\left(x\right)$.
- Построить график $y=f\left(x+l\right)$, где $l > 0$? Сдвинуть график $y=f\left(x\right)$ вдоль оси $OX$ на $l$ единиц масштаба влево.
- Построить график $y=f\left(x-l\right)$, где $l < 0$? Сдвинуть график $y=f\left(x\right)$ вдоль оси $OX$ на $l$ единиц масштаба вправо.
Как построить график функции $y=f\left(x\right)+m$, если известен график функции $y=f\left(x\right)$.
- Построить график $y=f\left(x\right)+m$, где $m > 0$? Сдвинуть график $y=f\left(x\right)$ вдоль оси $OY$ на $m$ единиц масштаба вверх;
- Построить график $y=f\left(x\right)-m$, где $m > 0$? Сдвинуть график $y=f\left(x\right)$ вдоль оси $OY$ на $m$ единиц масштаба вниз.
Как построить график функции $y=f\left(x+l\right)+m$, если известен график функции $y=f\left(x\right)$.
- График функции $y=f\left(x+l\right)+m$ можно получить из графика $y=f\left(x\right)$ параллельными сдвигами по осям $OX$ и $OY$.
График Дробной Функции.
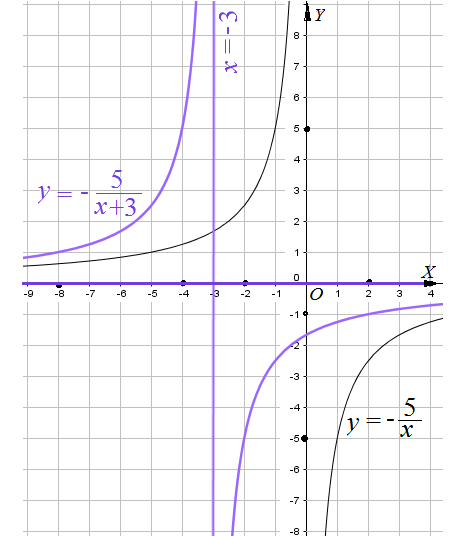
Пример 2: Построить график функции $y=-\frac{5}{x+3}$ .
- сначала построим график функции $y=-\frac{5}{x}$ ... от графика $y=\frac{1}{x}$ ... отразим от $OX$ и растянем по вертикали 5 раз.
- сдвинем получившуюся гиперболу вдоль оси $OX$ на $3$ единицы влево, получится требуемый график.
- это гипербола с асимптотами $x=-3$; $y=0$. "почему так?" - как мы строим графики?
- берем несколько $x$ - точек и находим для каждого свои $y$ - значения в соответствии "с формулой функции".
- По точкам проводим график. Очевидно, если, скажем, $x=0,52$ функция $y=-\frac{5}{x+3}$ дает какое-то значение,
- ... то, конечно для $x=3,52$ другая функция, $y=-\frac{5}{x}$ дает ровно такое же значение.
- значит, точки графиков будут различаться на $3$ единицы по $x$ - координате и совпадать по $y$ - координате.
- Ровно так и для всех точек. "Сравни две функции и вообрази их графики: каковы различия и что общего?"
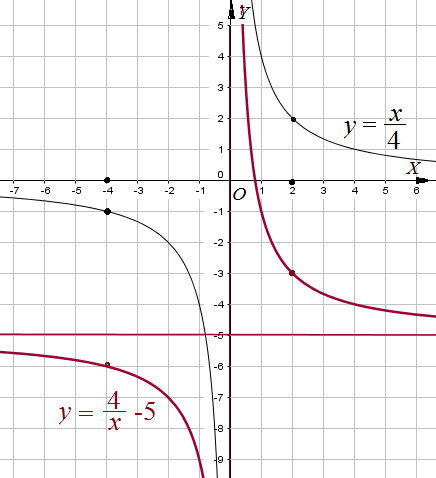
Пример 3: Построить график функции $y=\frac{4}{x}-5$ .
- Сначала надо построить график функции $y=\frac{4}{x}$ . Гиперболу $y=\frac{1}{x}$ "растянем" четыре раза.
- Сдвинуть получившуюся гиперболу вдоль оси $OY$ на $5$ клеточек вниз. Т.к. каждое значение должно отличаться на 5 единиц.
- получится требуемый график. Это гипербола с асимптотами $x=0$; $y=-5$.
- Важно знать где пересекается с нулем. Решение, корень $\frac{4}{x}-5=0$ дает абсциссу $x=0.8$. Точка графика $\left(0,8;0\right)$.
Вертикальная асимптота - $x=0$, проходит в полюсе, точке разрыва функции. Точка обнуления знаменателя. Параллельно $OY$.
Горизонтальная асисмптота -$y=-5$, линия, на которую "ложится" график при значениях $х$ около $+-\infty$. Параллельно $OX$.
Гипербола - график простой дроби, две асимптоты делят на 4 четверти, ветви гиперболы "зажаты - прижаты" к асимптотическим линиям .
Наклонная асимптота - линия типа $y=2x+3$, к которой "прижимаются" ветви графика "на" или "около" + - бесконечнoсти.
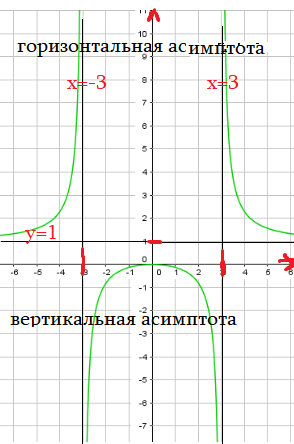
Пример 4: Построить график функции $y=\frac{x-5}{x^2-25}$
- Если выражение функции упрощается, то следует это сделать. Ибо получится функция проще, легче вычисляемая и рисуемая.
- Тождественное преобразование, сокращение $\frac{x-5}{x^2-25}=\frac{x-5}{(x+5)(x-5)}=\frac{1}{x+5}$. Так, что график $y=\frac{1}{x+5}$ ?
- Не спеши! Мы сократили на $x-5$ , которое незаконно для $x=5$. Нарушается О.Д.З - в исходной функции нет места $x=5$.
- Значит: можем строить гиперболу $y=\frac{1}{x+5}$ взамен нашей $y=\frac{x-5}{x^2-25}$, но "без точки $x=5$".
- Точка $x=5$ разрывает "гладкий" график гиперболы. Она называется "выколотая точка с координатами $\left(5;0,1\right)$".
Важно уметь исследовать функцию - график около точек разрыва. + / - поблизости. Куда тянется?
- Исследуем около $x=-5$. Возьмем "близкие" точки $-5,01$ и $-4,99$. Вычислим приближенные значения.
- Чуть левее ... $f\left(-5,01\right)=\frac{-5,01-5}{(-5,01)^2-5^2}\approx -100$. Чуть правее ... $f\left(-4,99\right)=\frac{-4,99-5}{(-4,99)^2-5^2}\approx 100$.
- Прямая $x=-5$ - вертикальная асимптота. Ветвь слева прижимается "вниз", к $-\infty$ . А справа поднимается вверх к $+\infty$.
- Около $x=5$. Чуть левее $f\left(4,99\right)=\frac{4,99-5}{4,99^2-5^2}\approx0,101$. $f\left(5,01\right)=\frac{5,01-5}{5,01^2-5^2}\approx0,099$.
- Значит, $x=5$ точка разрыва, на графике выколотая точка $\left(5;0,1\right)$. Т.к. в ней $y=\frac{1}{5+5}=0,1$.
- "О нулях": при $x=0$ $y=0,2$ . Но функция нигде не обнуляется, $y\ne0$. Прямая $y=0$ - горизонтальная асимптота.
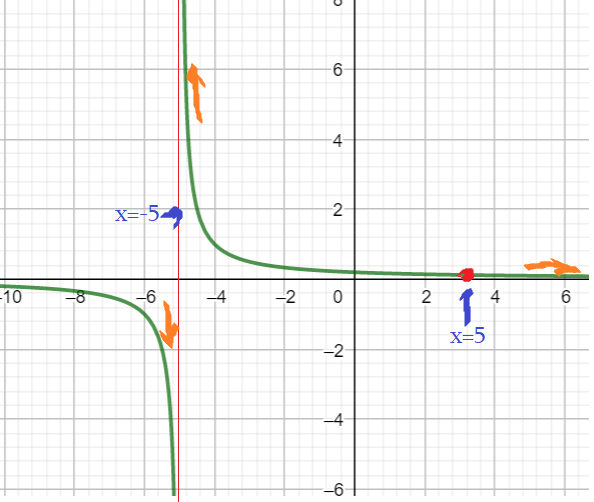
Пример 5: Построить график функции $y=\frac{x^2-16}{x+4}$
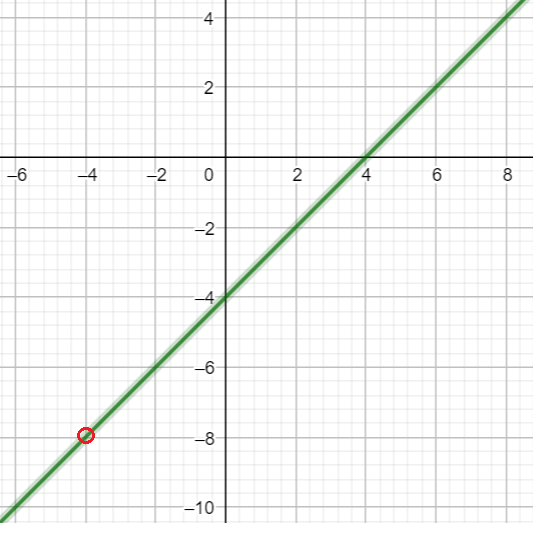
- О.Д.З функции $x\ne-4$. Оговорив это, со спокойной совестью сократим $y=\frac{x^2-16}{x+4}=x-4$.
- График нащей функции - прямая линия $y=x-4$ с выколотой точкой $\left(-4;-8\right)$ при $x=-4$.
- "Близко чуть левее": $x=-4,01$ значение $f\left(-4,01\right)=\frac{(-4,01)^2-16}{-4,01+4}=-8,01$. Ближе? ... Предел $\approx-8$.
- "О нулях". при $x=0$ $y=-4$ . Обнуление функции $y=0$ при $x=4$ - пересечение с $x$ - осью.
График Дробно - Рациональной Функции.
Определение: дробно-рациональной порядка $\left(n;m\right)$ называется функция вида $y=\frac{a\cdot x^n+5x^3-x+c}{b\cdot x^m-4x^2-7x+d}$
Числитель - многочлен степени $n$ , знаменатель - многочлен степени $m$ . Общий вид: $y=\frac{P\left(x\right)}{Q\left(x\right)}$
Нули функции - корни числителя $P\left(x\right)=0$ , Асимптоты (полюсы) - корни знаменателя $Q\left(x\right)=0$.
Пример 6: Построить график функции $y=\frac{x^2}{x^2-9}$.
- Функция $f\left(x\right)=\frac{x^2}{x^2-9}$ - четная: $f\left(x\right)=f\left(x\right)$ $f\left(8\right)=f\left(-8\right)$ - Слева и справа от $OY$ симметрично.
- Вычисления: $f\left(-4\right)=\frac{\left(-4\right)^2}{\left(-4\right)^2-9}=\frac{16}{7}\approx2,3$ $f\left(-10\right)=\frac{100}{91}\approx 1,1$ $f\left(-5\right)=\frac{25}{16}\approx 1,6$ $f\left(-3,5\right)=\frac{12.25}{3,25}\approx 3,8$
- $f\left(-2\right)=f\left(2\right)=\frac{4}{-5}\approx -0,8$ $f\left(-1\right)=f\left(1\right)\approx -0,1$ $f\left(3,5\right)\approx 3,8$ $f\left(4\right)\approx 2,3$ $f\left(5\right)\approx 1,6$ $f\left(10\right)\approx 1,1$
- Наша функция имеет нули в точке $x=0$ , а вертикальные асимтоты - линии $x=-3$ , $x=3$
- Асимптота - прямая линия, к которой "прижимается" график функции, "подходя" к ней бесконечно близко.
- Чему равно $\frac{x^2}{x^2-9}$ при очень больших $x$ ? $x\approx\pm1000$ ? Конечно, $y\approx1$ горизонтальная асимптота $y=1$ .
- Анализ графика: 1) Обнуляется при $x=0$ . 2) Значение в нуле : $y=\frac{x^2}{x^2-9}$ в $x=0$ равно $y=0$.
- 3) Поведение в разрывах: "чуть левее" полюса $x\approx-3-0,01$ значение $y > 0$ - "большое положительное".
- "чуть правее" разрыва $x\approx-3+0,01$ значение функции "большое отрицательное".
- Поведение около другого разрыва: когда $x$ "чуть левее" , например $x\approx3-0,01$ , то $y < 0$ ;
- когда $x$ "чуть правее" , например $x\approx3+0,01$ , то $y > 0$.
- 4) Поведение на бесконечности: при $x\approx\pm\infty$ значение "ложится" около $y\approx1$.
- 5) Область определения функции - все точки оси $x$ , кроме $x=\pm3$
- 6) Функция положительна $y > 0$ на интервалах $x < -3$ , $x > 3$.
- 7) Функция отрицательна $y < 0$ на интервалах $-3 < x < 0$ , $0 < x < 3$.
пробaп 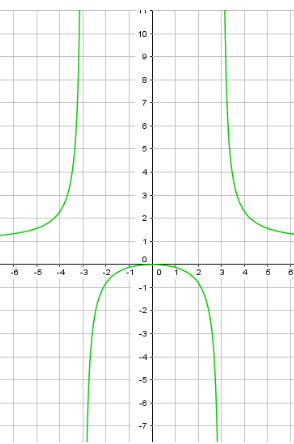
Графический способ решения уравнений
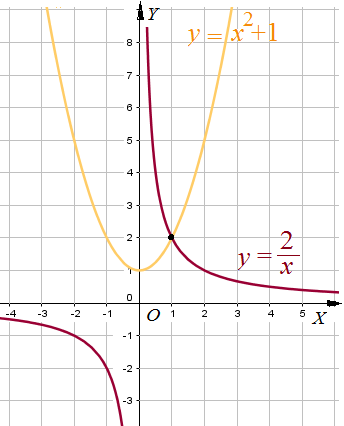
Пример 7: Решить уравнение $\frac{2}{x}=x^2+1$ графическим способом.
- Рассмотрим две функции : $y=\frac{2}{x}$ и $y=x^2+1$ построим гиперболу $y=\frac{2}{x}$ и параболу $y=x^2+1$ по
- чертежу видно, что графики пересекаются в точке с координатами $\left(1;2\right)$. если подставить $x=1$ в уравнение,
- то равенство выполняется: $\frac{2}{1}=1^2+1$ обе функции принимают одно и то же значение $2=2$.
- ответ: $x=1$. при таком $x$ графики пересекаются.
- "почему?": при каких $x$ - числах выравниваются обе части уравнения? при тех $x$ - числах, при которых левая
- функция и правая функция приобретают одинаковые значения ... это то же самое, что графики этих функций
- пересекаются в точках с такими $x$ - координатами.
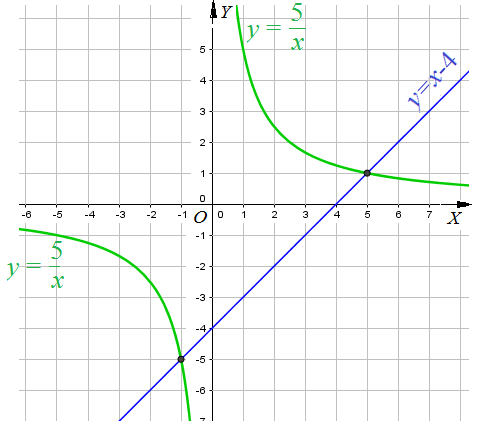
Пример 8: Решить уравнение $\frac{5}{x}=x-4$.
- рассмотрим две функции: $y=\frac{5}{x}$ и $y=x-4$, построим их графики: гиперболу $y=\frac{5}{x}$ и прямую $y=x-4$.
- по чертежу видно, что гипербола и прямая пересекаются в точках $(-1;-5)$ и $(5;1)$. проверим, подставим
- $x=-1$ и $x=5$ в уравнение : $\frac{5}{-1}=-1-4$ $\Leftrightarrow$ $-5=-5$ и $\frac{5}{5}=5-4$ $\Leftrightarrow$ $1=1$ . равенство
- выполняется, значит данное уравнение имеет два корня - абсциссы точек пересечения графиков.
- ответ: $x_1=-1$; $x_2=5$.
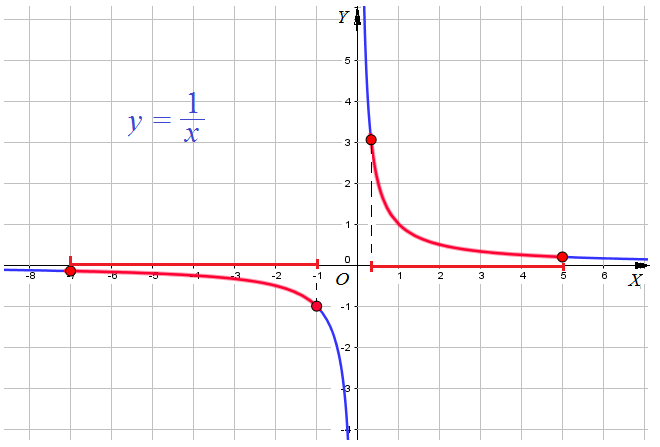
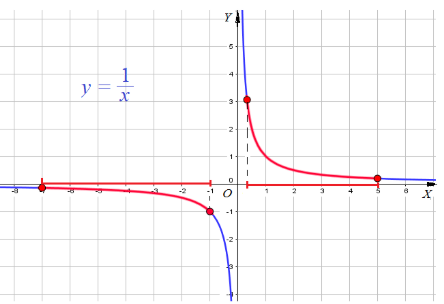
Пример 9: Найти наименьшее и наибольшее значения функции $y=\frac{1}{x}$ на отрезках а) $\left[\frac{1}{3};5\right]$ и б) $\left[-7;-1\right]$.
- Построим график функции $y=\frac{1}{x}$ .
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $\left[\frac{1}{3};5\right]$.
- Для выделенной части графика находим: наименьшее значение $y=\frac{1}{5}$ при $x=5$ , наибольшее $y=3$ при $x=\frac{1}{3}$.
- Выделим часть графика, соответствующую значениям переменной $x$ на отрезке $\left[-7;-1\right]$.
- Для выделенной части графика находим: наименьшее значение $y=-\frac{1}{7}$ при $x=-7$ наибольшее $y=-1$ при $x=-1$.
Пример 10: Доказать, что функция $y=f\left(x\right)$ , где $f\left(x\right)=\frac{4}{x}$
удовлетворяет соотношению $f\left(x-5\right)-f\left(x+1\right)=1,5\cdot f\left(x-5\right)\cdot f\left(x+1\right)$.
- Подставим в аргументы функций значения $x-5$ и $x+1$, получим: $f\left(x-5\right)=\frac{4}{x-5}$ и $f\left(x+1\right)=\frac{4}{x+1}$ .
- распишем левую часть тождества $f\left(x-5\right)-f\left(x+1\right)=\frac{4}{x-5}-\frac{4}{x+1}=\frac{4\left(x+1\right)-4\left(x-5\right)}{\left(x-5\right)\left(x+1\right)}=\frac{24}{\left(x-5\right)\left(x+1\right)}$. аналогично,
- с правой стороны получим $1,5\cdot f\left(x-5\right)\cdot f\left(x+1\right)=1,5\frac{4}{x-5}\cdot\frac{4}{x+1}=\frac{1,5\cdot16}{\left(x-5\right)\left(x+1\right)}=\frac{24}{\left(x-5\right)\left(x+1\right)}$. одинаковые! ч.т.д.
Упражнения
