Алгоритмы решения дробно-рациональных уравнений

Алгоритмы решения дробно-рациональных уравнений

• Уравнения        $\frac{x-2}{x+3}=0$ ,       $5y=\frac{2+4y}{3y-7}+14$   ,            $\frac{6x+5y}{11xy}=\frac{xy}{2x+12y}$        теряют смысл, если знаменатель станет нулем.
• ОДЗ    означает     "мы   пока   не   знаем   какие   числа   могут   уравнять, но   мы точно   знаем   какие не могут:
  
• перечисляем условия      ОДЗ,        чтобы не пропустить ложные числа.   Отфильтровать плохие, недопустимые числа."

Пример 1                  Решить уравнение              $\frac{3-2x}{x+2}=\frac{30}{5-x}$

• ОДЗ          $x+2\ne0$        $5-x\ne0$                (суть   написания    ОДЗ   -    не   допустить ложные   решения:   решением уравнения
  
• могут быть только те числа, будучи подставлеными в обе части уравнения    вместо    неизвестного   $x$,     уравняют обе части.)
• 1-ый шаг.        дробь равна дроби.       свойство пропорции:       если       $\frac{A}{B}=\frac{C}{D}$ ,    тогда      $A\cdot D=C\cdot B$.     значит, чтобы
• найти      $x$ ,     уравнивающий эти дроби,     достаточно найти    решения уравнения      $\left(3-2x\right)\left(5-x\right)=30\cdot\left(x+2\right)$ ,       
  
• 2-ой шаг.         раскрыв скобки, перейти к решению квадратного    уравнения             $15-3x-10x+2x^2=30x+60$        
  
• $\Leftrightarrow$                    $2x^2-43x-45=0$               $\Leftrightarrow$              решения уравнения :            $x_1=22,5$;            $x_2=-1$ .
  
• осталось проверить     ОДЗ     условия        $\Rightarrow$        оба числа принадлежат ОДЗ,     значит    это     корни     уравнения.

Алгоритм   решения    уравнения     "дробь   =   дробь"

$\frac{A\left(x\right)}{B\left(x\right)}=\frac{C\left(x\right)}{D\left(x\right)}$       решается   переходом   к квадратному по свойству   пропорций         $\Rightarrow$     $A\left(x\right)\cdot D\left(x\right)=C\left(x\right)\cdot B\left(x\right)$ .

$1)$:           $\frac{x^2-3x}{7-2x}=\frac{x+1}{5}$               $\Rightarrow$             $\left(x^2-3x\right)\cdot5=\left(x+1\right)\cdot\left(7-2x\right)$ .

$2)$:           $\frac{x^2-17}{5-x}=-1$              $\Rightarrow$              $x^2-17=-1\cdot\left(5-x\right)$

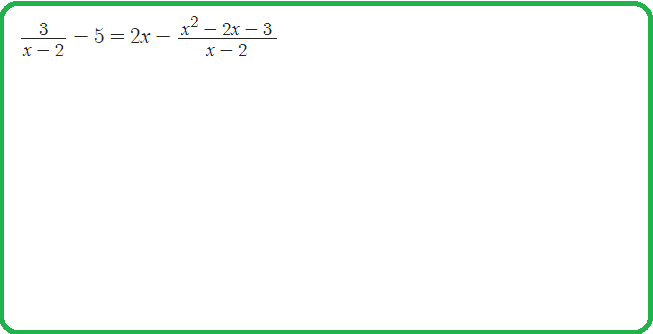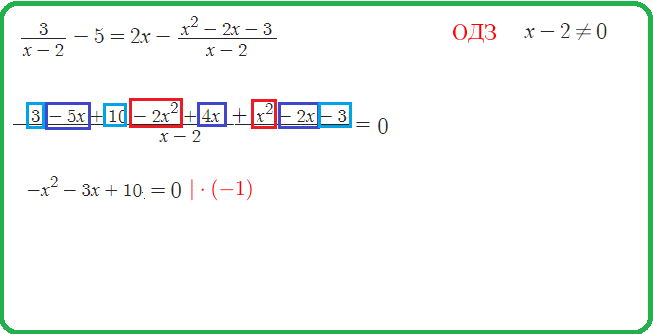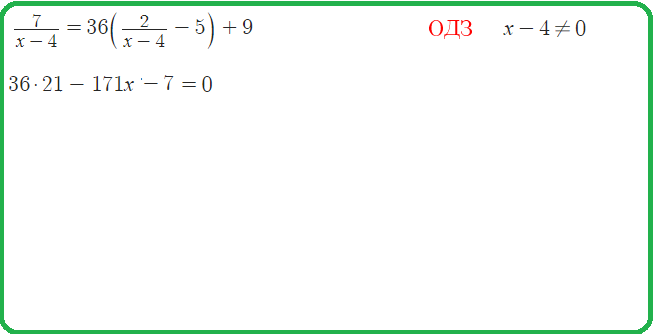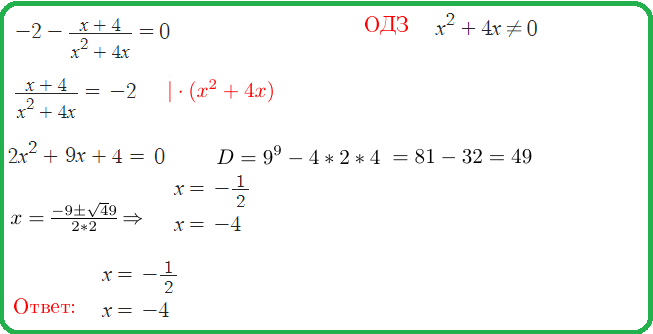
Пример 2:                  Решить уравнение              $\frac{x^2-5x+6}{x^2-9}=0$           

• ОДЗ         $x^2-9\ne0$         ( знаменатель    не может быть    равен    $0$ , значит     $x$     не может быть равен     $+3$       и      $-3$    .)
• в нашем уравнении     " дробь     =     ноль "       $\Leftrightarrow$      простое рассуждение:      вся   дробь равна нулю   значит,   числитель
  
• равен нулю.    как иначе дробь обнулится?      Никак!          $x^2-5x+6=0$           $\Leftrightarrow$        $D=5^2-4\cdot1\cdot6 = 1$         получаем
  
• $x_1=2$         $x_2=3$ ,       проверим    истинность решений:      $x=3$    оно   не   удовлетворяет   условию   ОДЗ ,       значит,
• это ложный корень.                 ответ:    $x=2$

Алгоритм     решения    уравнения     "дробь   =   0" :

$\frac{A\left(x\right)}{B\left(x\right)}=0$        эквивалентно         $\Leftrightarrow$         $A\left(x\right)=0$          $B\left(x\right)\ne0$ .     числитель $= 0$,       знаменатель   $\ne0$.

Пример 3:                  Решить уравнение              $\frac{x^2-7}{x-3}=\frac{2}{x-3}+12$                  

• ОДЗ             $x-3\ne0$
• приведем к    общему    знаменателю             $\frac{x^2-7}{x-3}=\frac{2}{x-3}+\frac{12\left(x-3\right)}{x-3}$    , сложим    числители   справа             $\frac{x^2-7}{x-3}=\frac{2+12\left(x-3\right)}{x-3}$,
  
• избавимся   от дробей   путем   домножения   обеих   частей   уравнения   на общий знаменатель         $x^2-7=2+12\left(x-3\right)$ ,
  
• перенесем в левую часть и получим желаемое уравнение       $x^2-12x+27=0$       $\Leftrightarrow$          $x_1=3$ ;       $x_2=9$ .    
  
• проверим: принадлежат ли    корни   ОДЗ уравнения   ( $x-3\ne0$   ) ? .    корень      $x=3$     не удовлетворяет ОДЗ   ,
  
• за это его исключают из множества решений.           такие корни называют посторонними,    ложными   корнями.
• ответ:    $x=9$

Алгоритм   решения   дробно-рациональных   уравнений:

1. определить   условия   ОДЗ   уравнения.   какие   выражения   не   могут   быть   нулем?

2. привести   все   слагаемые   в   обеих   частях   уравнения   к   общему   знаменателю.

3. домножить   обе   части   уравнения   на   общий   знаменатель.   сократить.

4. найти и корни,   решения   полученного   уравнения.

5. проверить,   принадлежат ли   найденные   корни   ОДЗ.

6. записать   в   ответе   те   из   найденных    корней,   которые   принадлежат   ОДЗ.

Алгоритм     решения     уравнения      "дробно - рациональное выражение    =      дробь":

https://studfile.net/preview/8958140/page:3/

Интерактивная Доска

Упражнения