Квадратное уравнение называется приведенным , если коэффициент при $x^2$ равен единице: $x^2+bx+c=0$
Если в таком уравнении $b$ - четное число , т.е. его можно представить как $2p$ , то приведенное $x^2+2px+q=0$
можно решать по упрощенным формулам .
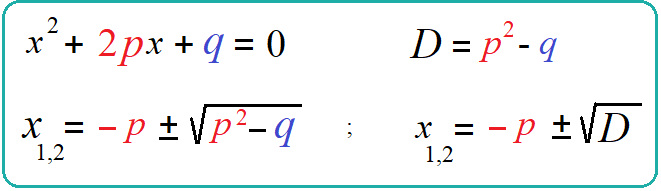
Внимание: в формуле Дискриминанта нет умножения на $4$ !
Пример 1: Решение приведенного уравнения $x^2+6x-7=0$
- в данном приведенном уравнении линейный коэффициент четный $2p = 6$ $\Rightarrow$ $p = 3$ , значит
- можно применить упрощенные формулы. вычислим Дискриминант, узнаем есть ли у данного уравнения корни:
- $D=3^2-(-7)=9+7=16$ , получили $D>0$ $\Rightarrow$ уравнение имеет два корня: $x_1=-p+\sqrt{D}=-3+4=1$ ,
- и $x_2=-p-\sqrt{D}=-3-4=-7$ Ответ: $x_1=1$ , $x_2=-7$
Пример 2: Решение уравнения $x^2-6x+3=0$
- $-6 =2p$ $\Rightarrow$ $p =-3$ . Для приведенного уравнения с четным коэффициентом можно использовать ...
- упрощенную формулу корней $x_1=-p+\sqrt{p^2-q}=3+\sqrt{9-3}=3+\sqrt{6}$ , $x_2=-p-\sqrt{p^2-q}=3-\sqrt{6}$
- Ответ: $x_1=3+\sqrt{6}$ , $x_2=3-\sqrt{6}$
Помните! Все упрощенные формулы $D=p^2-q$ ; $x=-p+\sqrt{D}$ ; $x=-p-\sqrt{D}$
$x=-p+\sqrt{p^2-q}$ ; $x=-p-\sqrt{p^2-q}$ можно применять
пробa только для приведенных квадратных уравнений с четным линейным коэффициентом.
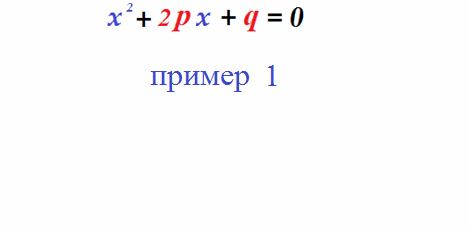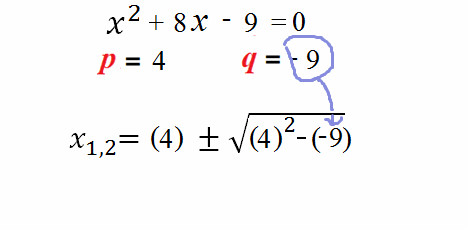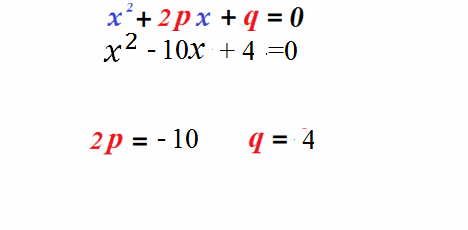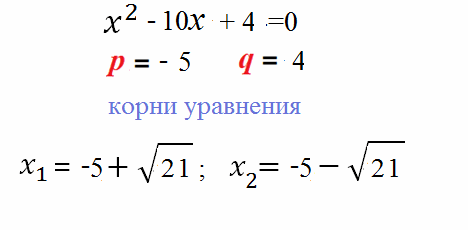

Пример 3: Решение уравнения $x^2-8x+26=0$
- определим коэффициенты $2p=-8$ $\Rightarrow$ $p=-4$ ; $q=26$ и найдем дискриминант этого уравнения:
- $D=p^2-q=\left(-4\right)^2-26=16-26=-10 < 0 $ - он отрицательный, значит Ответ: корней нет!
Как быть, если в уравнении перед $x^2$ стоит "$-$" .
Пример 4: Решение уравнения $-x^2+8x-3=0$
- это уравнение не является приведенным , ведь первый коэффициент ($-1$) , т.е. не равен еденице
- и значит упрощенные формулы применять нельзя. Это легко исправить, умножив все уравнение на $(-1)$ $\Rightarrow$
- $x^2-8x+3=0$ $\Leftrightarrow$ теперь можно использовать упрощенные формулы : $D=\left(-4\right)^2-3=13$,
- Ответ: $x_1=4+\sqrt{13}$ , $x_2=4-\sqrt{13}$
Интерактивная Доска:
Упражнения:
Послесловие:
Если скорость Ваших исполнений низкая, часто допускаете ошибки, пройдите Тест-упражнение несколько раз.
Откройте Тест-Упражнение через "Решать заново" следующим образом:
Наведите курсор мышки на это упражнение , в появившемся меню выберите пункт "Решать заново" .
Тест-Упражнение откроется с новыми, но аналогичными примерами , так вы получите "новое" задание.
