Основное свойство дроби: Если числитель и знаменатель алгебраической дроби поделить на одно и то же ненулевое выражение, то получится алгебраическая дробь, равная прежней: дробь не изменится.
$\frac{A\cdot X}{X\cdot B}=\frac{A\cdot X:X}{X\cdot B:X}=\frac{A\cdot1}{1\cdot B}=\frac{A}{B}$ $X\ne0$ $B\ne0$
Сократить дробь - значит разделить числитель и знаменатель этой дроби на один и тот же множитель.
Алгоритм сокращения алгебраических дробей
- Разложить числитель и знаменатель дроби на множители.
- Найти общие множители.
- Разделить числитель и знаменатель на общие множители.
Пример 2: Сократить дроби $\frac{7a}{ax}$ $\frac{6m}{-9m}$ $\frac{10ab^6c}{15a^3b^2x}$ $\frac{8\left(a-b\right)}{a-b}$
$\frac{7a}{ax}=\frac{7\cdot a}{a\cdot x}=\frac{7\cdot [a]}{[a]\cdot x}=\frac{7\cdot [1]}{[1]\cdot x}=\frac{7}{x}$ общий множитель $a$
$\frac{6m}{-9m}=\frac{6\cdot [m]}{-9\cdot [m]}=\frac{2\cdot3\cdot [1]}{-3\cdot3\cdot [1]}=-\frac{2}{3}$ общий множитель $3m$
$\frac{10ab^6c}{15a^3b^2x}=\frac{10ab^6c:[5ab^2]}{15a^3b^2x:[5ab^2]}=\frac{2b^4c}{3a^2x}$ общий множитель $5ab^2$
$\frac{8\left(a-b\right)}{a-b}=\frac{8\left(a-b\right):[a-b]}{(a-b):[a-b]}=8$ общий множитель $a-b$
Пример 3: Сократить алгебраические дроби


Пример 4: Сократить дробь $\frac{x^2+5x}{25-x^2}$
- Разложим числитель и знаменатель на множители: в числителе - вынос за скобки, в знаменателе - формула:
- $\frac{x^2+5x}{25-x^2}=\frac{x\left(x+5\right)}{\left(5-x\right)\left(5+x\right)}$
- Появился общий множитель $x+5$. Сократим и числитель и знаменатель на общий множитель. Т.е. Поделим:
- $\frac{x^2+5x}{25-x^2}=\frac{x\left(x+5\right)}{\left(5-x\right)\left(5+x\right)}=\frac{x}{5-x}$
Пример 5: Сократить дробь $\frac{a^2+4a+4}{a^2-4}$
- В числителе формула полного квадрата, в знаменателе- формула разности квадратов. Разложим их:
- $\frac{a^2+4a+4}{a^2-4}=\frac{(a+2)^2}{(a-2)(a+2)}$
- Вдруг, откуда - то (?) Появился общий множитель $a+2$. Сократим и числитель и знаменатель на нее:
- $\frac{a^2+4a+4}{a^2-4}=\frac{(a+2)^2}{(a-2)(a+2)}=\frac{a+2}{a-2}$
Пример 6: Сократить дробь $\frac{x^2-6x-7}{x+1}$
- В числителе выделим полный квадрат, Разложим по формуле разности квадратов:
- $\frac{x^2-6x-7}{x+1}=\frac{x^2-6x+9-9-7}{x+1}=\frac{\left(x-3\right)^2-16}{x+1}=\frac{\left(x-3-4\right)\left(x-3+4\right)}{x+1}=\frac{\left(x-7\right)\left(x+1\right)}{x+1}=x-7$
- Вдруг, откуда - то (?) появился общий множитель $x+1$. Сократим и числитель и знаменатель на нее:

Примеры для закрепления:
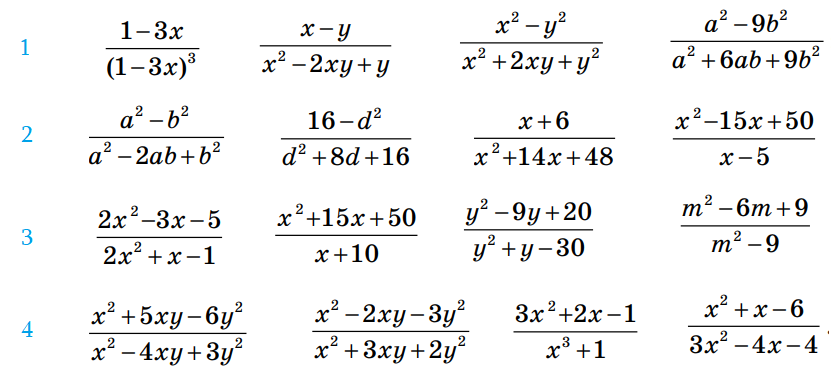
Упражнения
