Напоминание о числовых дробях: Сложение, Вычитание, Сравнение
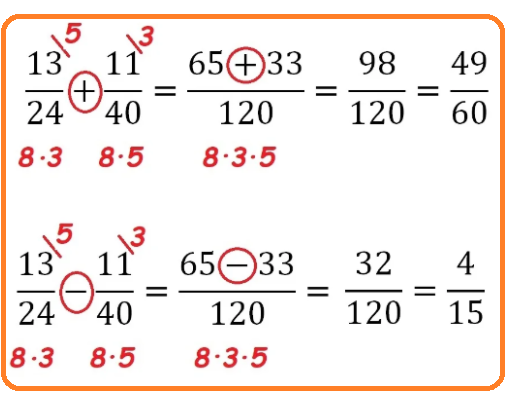
Правило: Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями, надо:
- привести данные дроби к наименьшему общему знаменателю;
- сравнить (сложить, вычесть) полученные дроби
Пример 1: Дроби: $\frac{2}{3}$ и $\frac{3}{5}$. Сложить, Вычесть, Сравнить.
- Сложение дробей: $\frac{2}{3} + \frac{3}{5}$ .
- приведем дроби к наименьшему общему знаменателю 15.
- Сложим $\frac{2}{3}+\frac{3}{5}=\frac{2\cdot5}{15}+\frac{3\cdot3}{15}=\frac{10}{15}+\frac{9}{15}=\frac{19}{15}=1\frac{4}{15}$
- Вычитание дробей: $\frac{2}{3} - \frac{3}{5}$ .
- $\frac{2}{3} -\frac{3}{5}= \frac{2}{3}-\frac{3}{5}=\frac{2\cdot5}{15}-\frac{3\cdot3}{15}=\frac{10}{15}-\frac{9}{15}=\frac{10-9}{15}=\frac{1}{15}$
- Сравнение дробей: $\frac{2}{3}$ и $\frac{3}{5}$.
- первая дробь равна $\frac{10}{15}$ , вторая $\frac{9}{15}$ . При одинаковых знаменателях у первой дроби числитель больше:
- $\frac{10}{15} > \frac{9}{15}$ $\Rightarrow$ $\frac{2}{3}>\frac{3}{5}$ .
Правило: привести дроби к наименьшему общему знаменателю - значит выполнить следующее:
- найти Н.О.К их знаменателей. ... (наименьшее число, которое делится на оба знаменателя!)
- найти дополнительный множитель для каждой дроби по-отдельности: = ( Н.О.К ) : (его знаменатель) !
- вычислить числитель новой дроби: = (старый числитель) * (свой дополнительный множитель ) .
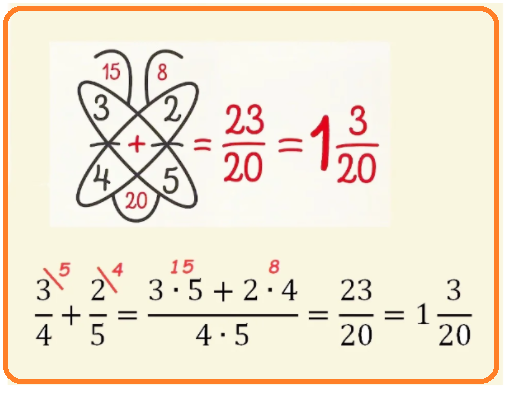
Сложение, вычитание алгебраических дробей: Одинаковые знаменатели
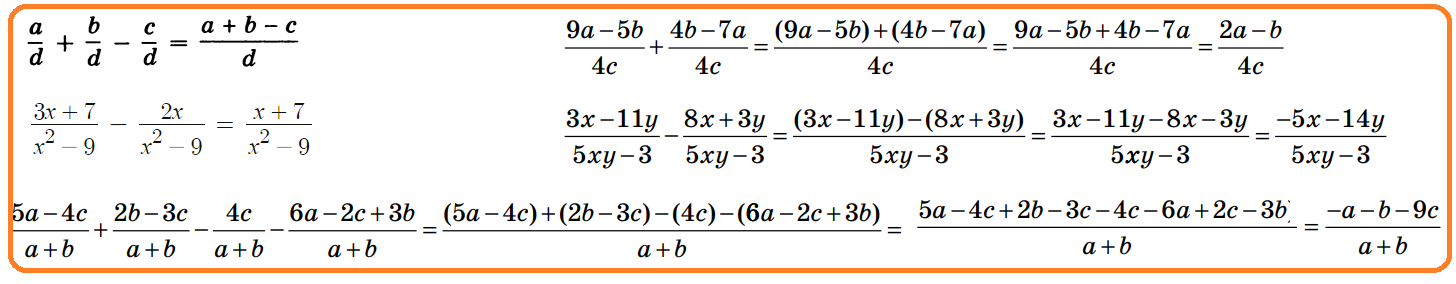
Правило: Сложение/вычитание дробей с одинаковыми знаменателями равен дроби с таким же знаменателем, а в числителе надо сложить/вычесть числители исходных дробей.
-
Общая форма для такого сложения/вычитания $\frac{A}{D}+\frac{B}{D}=\frac{A+B}{D}$ $\frac{A}{D}-\frac{B}{D}=\frac{A-(B)}{D}$
-
Внимательно: при знаке "-" следует заключать в скобки $\frac{A}{D}-\frac{B-C}{D}=\frac{A-\left(B-C\right)}{D}$
-
Каждый числитель со своим знаком и в скобках: $\frac{A}{D}-\frac{B}{D}+\frac{C}{D}-\frac{K}{D}=+\frac{\left(A\right)-\left(B\right)+\left(C\right)-\left(K\right)}{D}$
-
Противоположные Знаменатели, надо "поменять знак": $\frac{5}{y-4}-\frac{1}{4-y}=\frac{5}{y-4}-\frac{1}{-\left(y-4\right)}=\frac{5}{y-4}+\frac{1}{y-4}=\frac{\left(5\right)+\left(1\right)}{y-4}$

Пример 2: $\frac{11-a}{3a-b}-\frac{4-b}{3a-b}+\frac{7}{b-3a}$
- Смотрим на знаменатели: $3a-b$ и $b-3a$ . Противоположные! Нехитро меняем знак: $b-3a=-\left(3a-b\right)$
- Поменяем знаменатель 3-ей дроби на противоположное: $\frac{11-a}{3a-b}-\frac{4-b}{3a-b}+\frac{7}{-\left(3a-b\right)}$
- "Перебросим знак вперед": $\frac{11-a}{3a-b}-\frac{4-b}{3a-b}-\frac{7}{3a-b}$ - теперь, все знаменатели одинаковые.
- Складываем числители: $\frac{\left(11-a\right)-\left(4-b\right)-\left(7\right)}{3a-b}$ - каждый в своей скобке и со своим знаком.
- Раскрываем аккуратно скобки и упрощаем $=\frac{11-a-4+b-7}{3a-b}=\frac{b-a}{3a-b}$. Итого:
- $\frac{11-a}{3a-b}-\frac{4-b}{3a-b}+\frac{7}{b-3a}=\frac{11-a}{3a-b}-\frac{4-b}{3a-b}+\frac{7}{-\left(3a-b\right)}=\frac{11-a}{3a-b}-\frac{4-b}{3a-b}-\frac{7}{3a-b}=\frac{\left(11-a\right)-\left(4-b\right)-\left(7\right)}{3a-b}=\frac{11-a-4+b-7}{3a-b}=\frac{b-a}{3a-b}$
Сложение, вычитание алгебраических дробей с числовыми знаменателями
Пример 3: Вычесть дроби. $\frac{5x}{18}-\frac{7y}{12}$
- Смотрим на знамeнатели: к какому общему знаменателю можем привести? НОК - наименьшее число, кратное 18 и 12.
- НОК этих чисел 36. Какие дополнительные множители? К первой дроби 2, а ко второй дроби 3.
- $\frac{5x}{18}-\frac{7y}{12}=\frac{5x\cdot\left[2\right]}{36}-\frac{7y\cdot\left[3\right]}{36}=\frac{10x-21y}{36}$
- Замечание: фактически, мы умножили числитель и знаменатель 1-ой дроби на 2; Аналогично для 2-ой дроби на 3. "основное свойство"
- Таким образом получили в обеих дробьях одинаковые знаменатели, 36 и 36. И сложение-вычитание дробей с одинаковыми знаменателями.
Правило: 1. найти Н.О.К их знаменателей. Это и будет общим знаменателем... 2. найти дополнительные множители для каждой дроби по-отдельности: = ( Общее ) : (его знаменатель) 3. вычислить числители "приведенных" дробей: = (старый числитель) * (свой дополнительный множитель ) .
Сложение, вычитание алгебраических дробей с разными знаменателями
Основное свойство алгебраической дроби – Дробь не изменится, если числитель и знаменатель дроби одновременно умножать или делить на одно и то же. Хоть на многочлен, одночлен, число не 0, или на любое выражение.
Пример 4: Вычесть дроби $\frac{3}{a+b}-\frac{b-2}{2a}$
- Умножим числитель и знаменатель 1-ой дроби $\frac{3}{a+b}$ на знаменатель второго $2a$: дробь не изменится.
- Аналогично, во второй дроби $\frac{b-2}{2a}$ на числитель первого $a+b$ : дробь останется прежным.
- Идея: Эти дроби не изменятся, но знаменатели станут одинаковыми - как произведение прежных ... общий знаменатель.
- При этом числители каждой дроби приобретут свои дополнительные множители .... умножается на знаменатель другой дроби
- $\frac{3}{a+b}-\frac{b-2}{2a}=\frac{3\cdot\left[2a\right]}{\left(a+b\right)\cdot2a}-\frac{\left(b-2\right)\cdot\left[a+b\right]}{2a\cdot\left(a+b\right)}$ Складываем по правилу ... $\frac{3\cdot\left[2a\right]}{\left(a+b\right)\cdot2a}-\frac{\left(b-2\right)\cdot\left[a+b\right]}{2a\cdot\left(a+b\right)}=\frac{3\cdot\left[2a\right]-\left(b-2\right)\cdot\left[a+b\right]}{2a\cdot\left(a+b\right)}$
- Аккуратно упрощаем полученный числитель: $\frac{6a-ab-b^2+2a+2b}{2a\cdot\left(a+b\right)}=\frac{4a-ab-b^2+2b}{2a\cdot\left(a+b\right)}$
- Шаги вычитания: $\frac{3}{a+b}-\frac{b-2}{2a}=\frac{3\cdot\left[2a\right]}{\left(a+b\right)\cdot2a}-\frac{\left(b-2\right)\cdot\left[a+b\right]}{2a\cdot\left(a+b\right)}=\frac{3\cdot\left[2a\right]-\left(b-2\right)\cdot\left[a+b\right]}{2a\cdot\left(a+b\right)}=\frac{6a-ab-b^2+2a+2b}{2a\cdot\left(a+b\right)}=\frac{4a-ab-b^2+2b}{2a\cdot\left(a+b\right)}$
Правило: для нахождения общего знаменателя для дробей со знаменателями, не имеющими общих делителей: для нахождения общего знаменателя их следует просто перемножить . В таком случае дополнительным множителем для первой дроби будет знаменатель второй дроби, аналогично для второй дроби.
$\frac{A}{B}+\frac{C}{D}=\frac{A\cdot\left[D\right]+C\cdot\left[B\right]}{B\cdot D}$ $\frac{A}{B}-\frac{C}{D}=\frac{A\cdot\left[D\right]-(C)\cdot\left[B\right]}{B\cdot D}$
Это правило, как работало для случая обыкновенных дробей, так же работает для алгебраических и является универсальным для всех случаев нахождения общего знаменателя, даже, если у знаменателей есть общие делители. Просто в таком случае, применяя это правило, мы найдем не наименьший общий делитель, что не так оптимально для решения.
Сложение, вычитание алгебраических дробей: Наименьший Общий Знаменатель
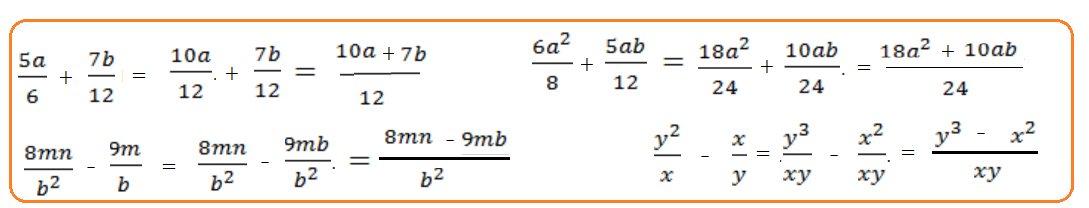
Пример 5: $\frac{3}{10c^5}+\frac{2}{15c^3}$
- Нам нужно найти наименьший, наилучший общий знаменатель. Для поиска такого "заглянем внутрь" каждого знаменателя.
- Разложим знаменатели $10c^5$ и $15c^3$ на множители: $10c^5=2\cdot5\cdot c^3\cdot c^2$ , $15c^3=3\cdot5\cdot c^3$
- Преобразуем знаменатели $\frac{3}{2\cdot5\cdot c^3\cdot c^2}+\frac{2}{3\cdot5\cdot c^3}$ . У каждого обнаружился множитель $5\cdot c^3$
- Первый состоит из множителей $\left[2c^2\right]$ и $5\cdot c^3$/$ . А второй состоит из множителей $3$ и $5\cdot c^3$.
- Сконструируем наименьшее общее: $(\left[2c^2\right]) \cdot (5\cdot c^3) \cdot (3) $ - здесь учтен общее $5\cdot c^3$ один раз!
- Если первую дробь, его числитель и знаменатель умножить на дополнительный множитель $3$, то получится нужный знаменатель.
- Аналогично, если во второй дроби умножать на дополнительный множитель $\left[2c^2\right]$, то и у нее будет такой же знаменатель.
- Сложим дроби с общим знаменателем: $\frac{3\cdot\left[3\right]+2\cdot\left[2c^2\right]}{2c^2\cdot3\cdot5c^3}$ - числители умножены на свои дополнительные множители.
- Упростим: $\frac{3}{10c^5}+\frac{2}{15c^3}=\frac{3}{2\cdot5\cdot c^3\cdot c^2}+\frac{2}{3\cdot5\cdot c^3}=\frac{3\cdot\left[3\right]+2\cdot\left[2c^2\right]}{2c^2\cdot3\cdot5c^3}=\frac{9+4c^2}{30c^5}$
Правило: Приведение к наименьшему общему знаменателю .
$\frac{A}{B\cdot M}+\frac{C}{D\cdot M}=\frac{A\cdot\left[D\right]+C\cdot\left[B\right]}{B\cdot D\cdot M}$ $\frac{A}{B\cdot M}-\frac{C}{D\cdot M}=\frac{A\cdot\left[D\right]-C\cdot\left[B\right]}{B\cdot D\cdot M}$
- Разложить знаменатели каждой дроби на множители. ($B\cdot M$ и $D\cdot M$)
- Собрать все общие множители ($M$) , в каждом знаменателе общий множитель отделить от других множителей: ($B$ и $D$)
- Сконструировать наименьший общий знаменатель как произведения множителей каждого ... общее: $B\cdot D\cdot M$
- ... при этом общий множитель ($M$) учитывать лишь один раз!
- Дополнительными множителями для каждой дроби будет _недостающие до общего_ множители: ($D$ и $B$)
Дополнительный множитель – результат деления общего знаменателя на знаменатель соответствующей дроби. В школе обычно учат писать их над числителями соответствующих дробей, отделяя от них своеобразными «палочками». Полезнее писать в "особых скобках".
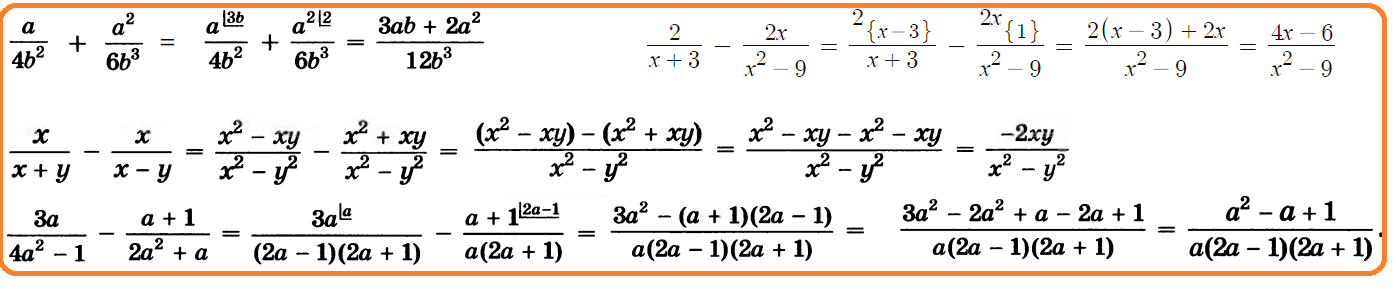
Пример 6: упростить $\frac{x^2}{x^2-6xy+9y^2}-\frac{x+3y}{2x-6y}$
- Разложим знаменатели: $x^2-6xy+9y^2$ - по формуле квадрата разности; $2x-6y$ - вынесем множитель $2$ за скобки.
- $\frac{x^2}{x^2-6xy+9y^2}-\frac{x+3y}{2x-6y}=\frac{x^2}{\left(x-3y\right)^2}-\frac{x+3y}{2\left(x-3y\right)}$ - знаменатели представлены множителями.
- Используем формулу сложения с НОК: $\frac{A}{B\cdot M}-\frac{C}{D\cdot M}=\frac{A\cdot\left[D\right]-C\cdot\left[B\right]}{B\cdot D\cdot M}$ Общий множитель $M=x-3y$ ;
- Кроме общего, у 1-го еще $B=x-3y$, у 2-го $D=2$ ; Наименьший знаменатель: $B\cdot D\cdot M=\left(x-3y\right)\cdot\left(2\right)\cdot\left(x-3y\right)$
- Реализуем: $\frac{x^2}{\left(x-3y\right)^2}-\frac{x+3y}{2\left(x-3y\right)}=\frac{x^2\cdot\left[2\right]-\left(x+3y\right)\left[x-3y\right]}{\left(x-3y\right)\cdot\left(2\right)\cdot\left(x-3y\right)}$
- Упростим, в числителе используем формулу разности квадратов: $\frac{2x^2-\left(x^2-9y^2\right)}{2\left(x-3y\right)^2}=\frac{x^2+9y^2}{2\left(x-3y\right)^2}$
- Итого: $\frac{x^2}{x^2-6xy+9y^2}-\frac{x+3y}{2x-6y}=\frac{x^2}{\left(x-3y\right)^2}-\frac{x+3y}{2\left(x-3y\right)}=\frac{x^2\cdot\left[2\right]-\left(x+3y\right)\left[x-3y\right]}{\left(x-3y\right)\cdot\left(2\right)\cdot\left(x-3y\right)}=\frac{2x^2-\left(x^2-9y^2\right)}{2\left(x-3y\right)^2}=\frac{x^2+9y^2}{2\left(x-3y\right)^2}$
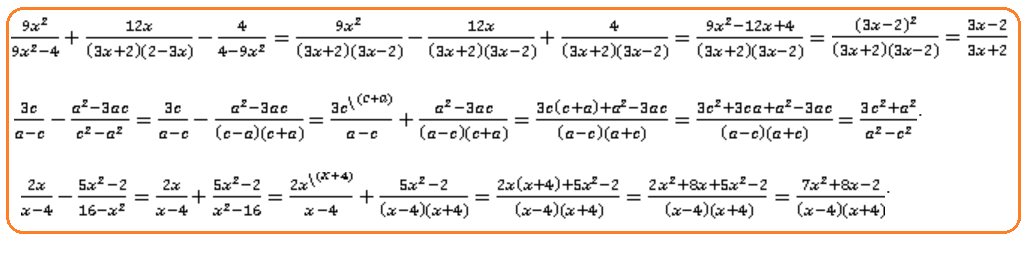
Упражнения:
