Как-то спросили: "зачем такое мудренное название". - Чтобы прониклись важностью, значимостью!
Во-первых, эти методы разложений применяются фактически всюду: 8 класс - квадратные уравнения, НОК алгебраических дробей, 9 класс - рациональные неравенства, 10 класс - показательные и тригонометрические уравнения, неравенства методом замены, 11 класс - однородные выражения, I курс - кривые второго порядка, интегралы простых форм, II курс - факторизация квадратичных форм, алгебра делителей
Во-вторых: Все-таки "факторизация" шире, чем просто "разложения": подразумевает увидеть факторы, делители, конструкцию "целое - его кусочки, корни", добиться легкости получения факторов, как элементарных составляющих
Разложение квадратного трехчлена угадыванием
Пример 1: Разложить на множители квадратный трехчлен $x^2+4\cdot x-21$
- Ищем разложение как представление в форме умножения двух скобок $\left(x+?\right)\left(x+?\right)$
- Ребус: Какие числа поставить вместо знаков "?", "?" так, чтобы после раскрытия скобок получилось $x^2+4\cdot x-21$
- ... проследите как открываются скобки .... умножение этих чисел должно привести к $-21$, а сложение к $4$.
- Легко угадать "чисто перебором", что таковыми будут числа -7 и 3: верно $\left(x-3\right)\left(x+7\right)=x^2+4\cdot x-21$
- процесс решения $x^2+4\cdot x-21$ = $\left(x+?\right)\left(x+?\right)$ = $\left(x-3\right)\left(x+7\right)$
- замечание: очевидно, что числа -7 и 3 являются корнями уравнения $x^2+4\cdot x-21=0$,
- т.к. уравнение при таком разложении распадается на обнуляющиеся факторы: $\left(x-3\right)$ и $\left(x+7\right)$
Пример 2: Разложить на множители трехчлен $5x^2-14\cdot x-3$
- Ищем разложение как представление в форме $\left(5x+?\right)\left(x+?\right)$ ... множитель 5 нужен для $5x^2$
- Какие числа вместо "?", "?" ... умножение этих чисел $-3$, а комбинация $5\cdot ?+?$ должно дать $-14$
- Угадать "чисто перебором" и чисел и знаков, что это числа -1 и 3: верно $\left(5x-1\right)\left(x+3\right)=5x^2-14\cdot x-3$
- процесс решения $5x^2-14\cdot x-3$ = $\left(5x+?\right)\left(x+?\right)$ = $\left(5x-1\right)\left(x+3\right)$ .
- факторы: $\left(5x-1\right)$ и $\left(x+3\right)$, корни уравнения $\frac{1}{5}$ и $-3$,
Пример 3: Разложить на множители трехчлен $6x^2+7\cdot x-20$
- Ищем представление в форме $\left(2x+?\right)\left(3x+?\right)$ ... множители 2 и 3 нужны для $6x^2$. А может 6 и 1 ?
- Каковы "?", "?" ... умножение дает $-20$, а комбинация $2\cdot ?+3\cdot ?$ должно привести к $7$
- Угадываем "чисто перебором вариантов" - числа 5 и -4: верно $\left(2x+5\right)\left(3x-4\right)=6x^2+7\cdot x-20$
- процесс решения $6x^2+7\cdot x-20$ = $\left(2x+?\right)\left(3x+?\right)$ = $\left(2x+5\right)\left(3x-4\right)$ .
- факторы: $\left(2x+5\right)$ и $\left(3x-4\right)$, корни уравнения $\frac{4}{3}$ и $-2,5$,
Разложение квадратного трехчлена по корням уравнения
Теорема Виета о разложении: если $x_1$ , $x_2$ корни уравнения $ax^2+bx+c=0$ , тогда верно тождество $ax^2+bx+c=a\cdot\left(x-x_1\right)\cdot\left(x-x_2\right)$
- Квадратное выражение через свои корни разлагается на множители. множители обнуляются при $x$ равном одному из корней.
- доказательство: раскроем скобки, перемножим слагаемые в правой части тождества
- $a\left(x-x_1\right)\left(x-x_2\right)=\left(x-x_1\right)\cdot\left(ax-ax_2\right)=ax\left(x-x_1\right)-ax_2\left(x-x_1\right)=a\cdot x^2-ax_1\cdot x-ax_2\cdot x+ax_1\cdot x_2=$
- группируем, приведем $x-$ подобные, $=a\cdot x^2+\left(-ax_1-ax_2\right)\cdot x+a\cdot x_1\cdot x_2=a\cdot x^2-a\left(x_1+x_2\right)\cdot x+a\cdot x_1\cdot x_2=$
- воспользуемся теоремой Виета "о сумме и произведении корней" $=a\cdot x^2-a\cdot\left(-\frac{b}{a}\right)\cdot x+a\cdot\frac{c}{a}=ax^2+bx+c$ ч.т.д.
Пример 4: Разложить на множители выражение: $-3x^2+7x+10$
- Какие корни у этого квадратичного выражения? какие решения у квадратного уравнения $-3x^2+7x+10=0$ ?
- Найдем через дискриминант: $D=7^2-4\cdot 10 \cdot (-3)=169$ . корни $x_1=\frac{-7+\sqrt169}{2\cdot (-3)}=-1$ $x_1=\frac{-7-13}{(-6)}=\frac{10}{3}$
- Тогда, по корням и коэффициенту $a=-3$ составим разложение по теореме Виета "о разложении":
- $-3x^2+7x+10=-3\cdot\left(x+1\right)\cdot\left(x-\frac{10}{3}\right)$ если еще упростить, то $=\left(x+1\right)\left(10-3x\right)$
Алгоритм нахождения корней квадратного трехчлена найзусть - угадывания корней:
- основано на Теорема: если есть целые корни, то они являются делителями свободного члена.
- Надо посмотреть на свободный коэффициент целочисленного квадратного уравнения; Перечислить все его делители.
- перебирая их и разные, возможные знаки ... искать и найти $2$ числа, обнуляющие квадратный трехчлен.
Пример 5: Разложить $y^2+y-12$ .
- Выписать все делители свободного члена $\pm1$, $\pm2$, $\pm3$, $\pm4$, $\pm6$, $\pm12$. Надо найти два числа таких, чтобы
- произведение было $+12$, а сумма $-1$. Перебрать разные пары и докопаться до двух чисел $3$ и $-4$ .
- разложим квадратный трехчлен $y^2+y-12=\left(y-3\right)\left(y+4\right)$
- Еще примеры:
- $x^2+4\cdot x-21$ делители $21$: корни $x=3$ и $x=-7$, факторы $\left(x-3\right)$ и $\left(x+7\right)$
- $x^2+2\cdot x-63$ делители $63$: корни $x=7$ и $x=-9$, факторы $\left(x-7\right)$ и $\left(x+9\right)$
- $x^2+10x-39$ делители $39$: корни $x=13$ и $x=-3$, факторы $\left(x-13\right)$ и $\left(x+3\right)$

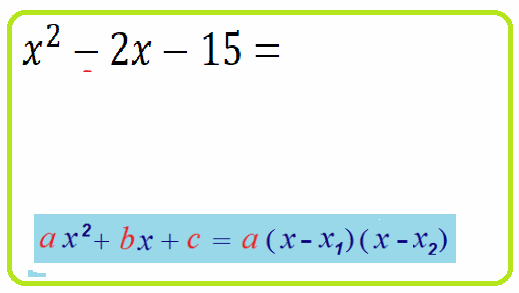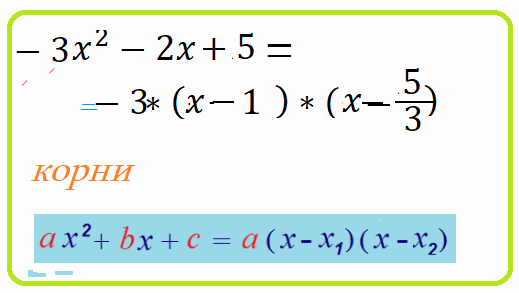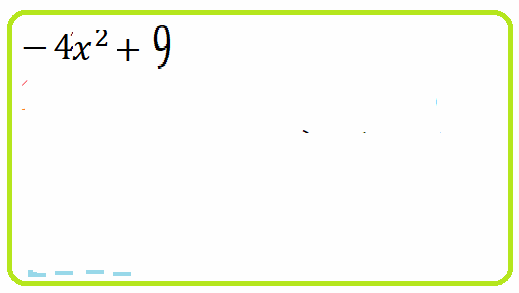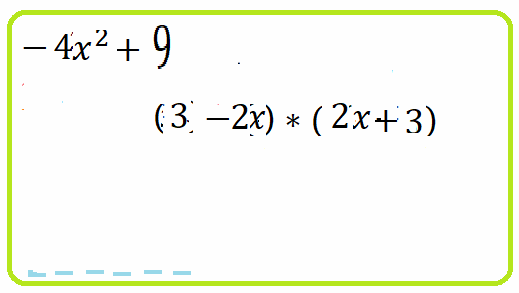
Разложение квадратных двухчленов
Пример 6: Разложить на множители путем выноса за скобки, по формулам:
- $5x^2-12x$ = ... вынесем общий множитель $x$ за скобки ... = $x\cdot (5x-12)$
- $7x-x^2$ = ... вынесем общий множитель $x$ за скобки ... = $x\cdot (7-x)$
- $16-x^2$ = ... разложим по формуле разности квадратов ... = $(4-x)\cdot (4+x)$
- $4x^2-25$ = ... разложим по формуле разности квадратов ... = $(2x-5)\cdot (2x+5)$
- $x^2-9a^2$ = ... разложим по формуле разности квадратов ... = $(x-3a)\cdot (x+3a)$
Разложение, факторизация квадратных форм
Пример 7: Разложить на множители квадратную форму $2a^2+7ab-15b^2$:
- Ищем представление по форме $\left(2a+?b\right)\left(a+?b\right)$ ... множитель 2 диктуется из-за $2a^2$.
- Каковы "?", "?" ... при открытии скобки как получатся $-15b^2$, а $7ab$ ?
- Перебором числовых вариантов придем к результату: $2a^2+7ab-15b^2=(2a+3b)\cdot (a-5b)$
- квадратичная форма состоит из факторов $(2a+3b)$ и $(a-5b)$
- Кстати: корнями уравнения $2x^2+7x-15=0$ являются числа $-\frac{3}{2}$ и $5$
- функция $2x^2+7x-15$ называется характеристической функцией квадратичной формы $2a^2+7ab-15b^2$
Пример 8: Разложить на множители $3\cdot 4^x-17\cdot 6^x+10\cdot 9^x$:
- Преобразуем к виду однородной: $3\cdot 4^x-17\cdot 6^x+10\cdot 9^x=3\cdot (2^x)^2-17\cdot (2^x)\cdot (3^x)+10\cdot (3^x)^2$
- Ищем представление по форме факторов $\left(3\cdot 2^x+?\cdot 3^x\right)\left(2^x+?\cdot 3^x\right)$ ...
- Каковы "?", "?" чтобы при открытии скобки получилось требуемое $3\cdot (2^x)^2-17\cdot (2^x)\cdot (3^x)+10\cdot (3^x)^2$ ?
- Перебором числовых коэффициентов придем к результату: $3\cdot 4^x-17\cdot 6^x+10\cdot 9^x=\left(3\cdot 2^x-2\cdot 3^x\right)\left(2^x-5\cdot 3^x\right)$
- Исходное показательное выражение состоит из факторов $\left(3\cdot 2^x-2\cdot 3^x\right)$ и $\left(2^x-5\cdot 3^x\right)$
- Такое разложение нам поможет эффективно решать уравнения и, особенно, неравенства.
Пример 9: Разложить на множители $\sin^2x+\sin x\cdot\cos x-6\cdot\cos^2x$:
- Тригонометрическое выражение имеет вид однородного порядка 2 . Суммарная степень каждого слагаемого - квадрат.
- Ищем представление по форме факторов $\left(\sin x-2\cdot\cos x\right)\left(\sin x+3\cdot\cos x\right)$ ...
- Каковы "?", "?" чтобы при открытии скобки получилось требуемое ......
- Перебором коэффициентов придем к результату: $\sin^2x+\sin x\cdot\cos x-6\cdot\cos^2x=\left(\sin x-2\cdot\cos x\right)\left(\sin x+3\cdot\cos x\right)$
- Исходное тригонометрическое выражение состоит из факторов $\left(\sin x-2\cdot\cos x\right)$ и $\left(\sin x+3\cdot\cos x\right)$
- Такое разложение нам поможет эффективно решать уравнения: приравнивая к нулю каждый фактор по отдельности.
Классная Интерактивная Доска:
Упражнения:
