Каноническое квадратное уравнение

Что такое обычное квадратное уравнение?
Это уравнение, в котором обязательно есть икс в квадрате. Видов квадратных уравнений много. Но самый «главный» ...

стандартный или канонический вид :       $a\cdot x^2+b\cdot x+c=0$      или     $0=a\cdot x^2+b\cdot x+c$

Числа    $a$ ,    $b$ ,     $c$      при неизвестном называются    коэффициентами уравнения .   У каждого свое название:

• $a$     называют квадратным      (т.к. он при $x^2$)           или первым   коэффициентом ;
• $b$     называют линейным           (т.к. он при $x$ )           или вторым    коэффициентом ;
• $c$     называют свободным членом уравнения           (т.к. он свободен от неизвестного)
• Важно правильно определять коэффициенты, ведь они участвуют в формулах решения квадратного уравнения!
• Особое внимание на знаки: в       $a\cdot x^2+b\cdot x+c=0$     написаны одни "плюсы", а в вашем уравнении могут быть и "минусы" !

   Определяем коэффициенты так:    

$0,2x^2+7x+13=0$      коэффициенты :         $a=0,2$     $b=7$         $c=13$

$3x^2-5x+10=0$          коэффициенты :         $a=3$      $b=-5$   минус!      $c=10$

$x^2-\frac{1}{3}x-5=0$           коэффициенты :         $a=1$;      $b=-\frac{1}{3}$           $c=-5$     минус!

$16x^2-25=0$                коэффициенты :         $a=16$       $b=0$         $c=-25$    минус!

$-\frac{1}{6}x^2-\frac{2}{3}x=0$            коэффициенты :         $a=-\frac{1}{6}$      $b=-\frac{2}{3}$   минус!        $c=0$

Внимание:       если дано нестандартное уравнение, чтобы не ошибиться в определении коэффициентов,
                           сначала перепишите его в стандартном виде :

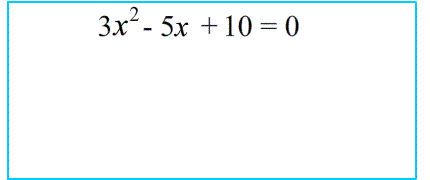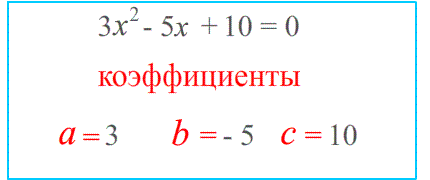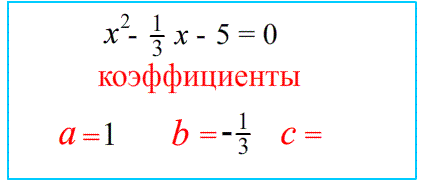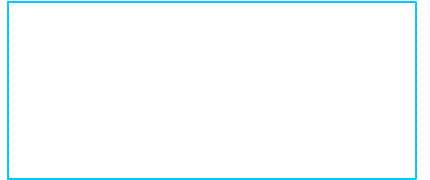
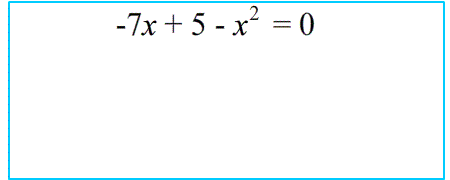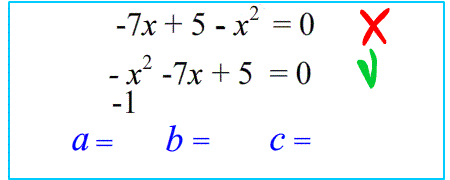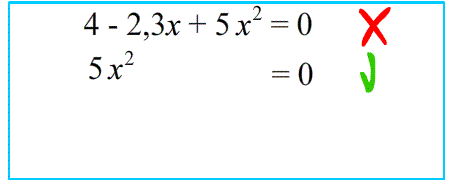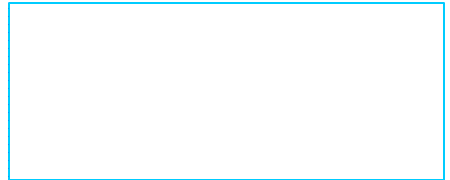
Формула решения канонического квадратного уравнения. Дискриминант

Канонический вид квадратного уравнения          $ax^2+bx+c=0$      ,              $a$, $b$, $c$ - коэффициенты уравнения.

Формула, составленная из трех коэффициентов уравнения              $D=b^2-4ac$         называется    Дискриминант .

Дискриминант помогает ответить на вопрос    "Есть ли у данного уравнения корни, сколько их ?"     и решить его.

            Формулы нахождения корней канонического квадратного уравнения:         

Пример 1        $x^2-3x-4=0$

• Определяем коэффициенты уравнения:    $a=1$   ,   $b=-3$    ,   $c=-4$
• Найдем Дискриминант    и выясним есть ли   корни у этого уравнения.
• Внимание!       Чтобы не ошибиться при подстановке отрицательного коэффициента в формулу, лучше заключить его в скобки:
• $D=b^2-4ac=\left(-3\right)^2-4\cdot 1\cdot\left(-4\right)=9+16=25$
• Т.к.    $D=25 > 0$ ,     значит уравнение имеет два корня ,
• найдем корни по формулам :       $x=\frac{-b+\sqrt{D}}{2a}=\frac{-\left(-3\right)+5}{2}=\frac{3+5}{2}=4$      и      $x=\frac{-b-\sqrt{D}}{2a}=\frac{-\left(-3\right)-5}{2}=\frac{3-5}{2}=-1$
•    Ответ:             $x=4$   ;     $x=-1$

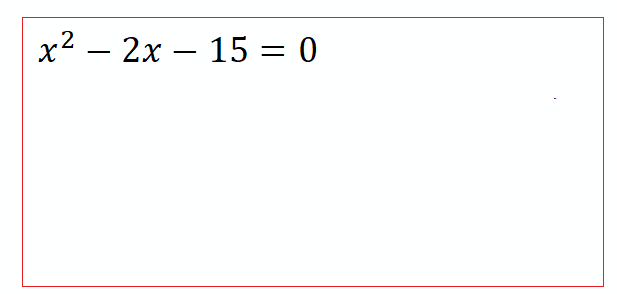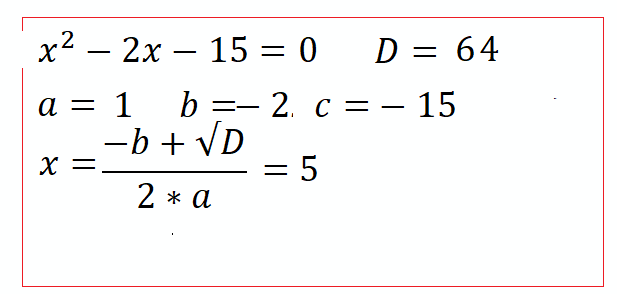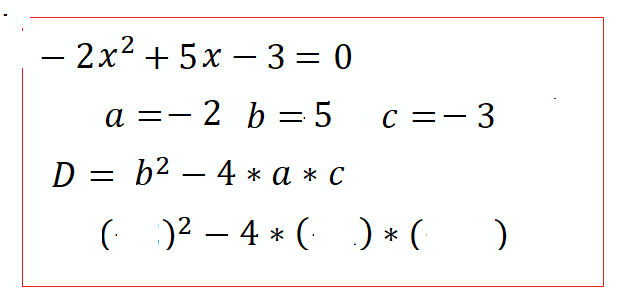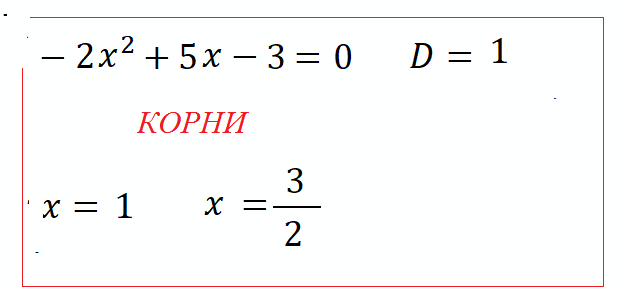
   Замечание:       Не всегда при извлечении корня из Дискриминанта получается целое число. В этом случае, решением уравнения будет дробное выражение с радикалом. Посмотрите внимательно, можно ли упростить полученное выражение ? Ответ должен быть всегда в сокращенном виде.

Пример 2:         $7x^2-2x-7=0$

• Определяем коэффициенты уравнения:    $a=7$   ,   $b=-2$    ,   $c=-7$
• $D=b^2-4ac=\left(-2\right)^2-4\cdot7\cdot\left(-7\right)=4+196=200.$           Т.к.    $D=200 > 0$ , значит уравнение имеет два корня :
• Внимание!     Окончательный ответ нужно давать всегда в сокращенном виде.
• 1) $x=\frac{-b+\sqrt{D}}{2a}=\frac{2+\sqrt{200}}{2\cdot7}$        в таком виде корень оставлять нельзя, т.к. дробь еще можно сократить:
• из-под корня можно вынести множитель 10, после возможно сокращение: $x=\frac{2+\sqrt{200}}{2\cdot7}=\frac{2+10\sqrt{2}}{2\cdot7}=\frac{1+5\sqrt{2}}{7}$;
• 2)   $x=\frac{-b-\sqrt{D}}{2a}=\frac{1-5\sqrt{2}}{7}$                             Ответ:             $x=\frac{1+5\sqrt{2}}{7}$ ;     $x=\frac{1-5\sqrt{2}}{7}$

Интерактивная Доска:

Упражнения:

Послесловие

Если скорость Ваших исполнений низкая, часто допускаете ошибки, пройдите Тест-упражнение несколько раз,