Что такое радикал?
Что такое радикал из числа? $\sqrt{2}$ ? Это такое положительное число, квадрат которого равняется $2$ .
Основное тождество: $\sqrt{a}$ - это неотрицательное число , чей квадрат $\left(\sqrt{a}\right)^2=a$ , равен подрадикальному $a$.
- проб Вот почему $\sqrt{49}=7$ , потому что $7^2$ равен $49$ .
- аналогично: $\sqrt{x^6}=x^3$ $\Leftrightarrow $ потому что $x^3$ в квадрате равен $x^6$.
- Кстати, $\sqrt{2}$ реально довольно "некрасивое" , очень длинное число $1,4142135624.... $
- гораздо удобнее сказать "радикал из 2" или "корень из 2". И это число приблизительно $\sqrt{2}\approx1,41$
- радикал - это математическая операция, обратная инверсия возведения в квадрат!
- А вот $\sqrt{2}\cdot\sqrt{8}$ вполне "приличное" число $4$. Потому что и произведение $\sqrt{2}\cdot\sqrt{8}$ и число $4$ в квадрате дают $16$.
- т.е. оба есть $\sqrt{16}$ - "радикал из $16$" или "корень квадратный из 16".
Внимание! Квадратный корень существует только от неотрицательного числа, $a\ge0$ и сам корень неотрицательный $\sqrt{a}\ge0$ .
Свойства радикалов:
$\left(\sqrt{a}\right)^2=a$ ; $\sqrt{a^2}=a$ - основные тождества . $\sqrt{9}\ne-3$
$\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}$ - радикал произведения. $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$ - радикал деления.
$\sqrt{a^2\cdot b}=a\cdot\sqrt{b}$ - вынос квадратного множителя за знак радикала, частичное извлечение корня $\sqrt{\frac{a}{b^2}}=\frac{\sqrt{a}}{b}$
$\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a}$ - избавление знаменателя от радикала
$\frac{1}{a-\sqrt{b}}=\frac{a+\sqrt{b}}{a^2-b}$ ; $\frac{1}{a+\sqrt{b}}=\frac{a-\sqrt{b}}{a^2-b}$ - умножение на сопряженное, избавление от радикала в знаменателе.
 пробел
пробел
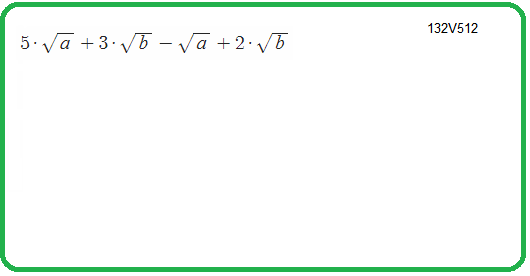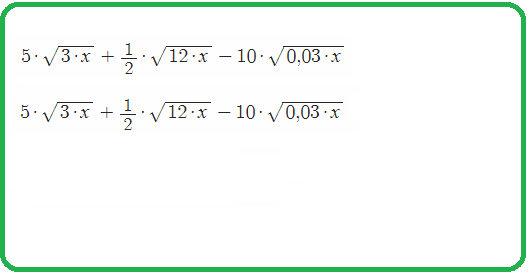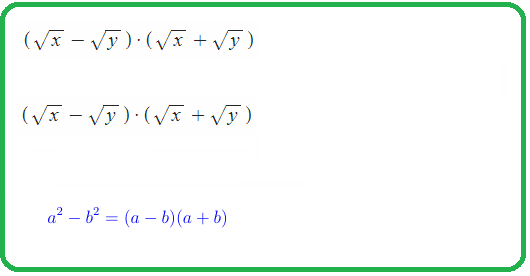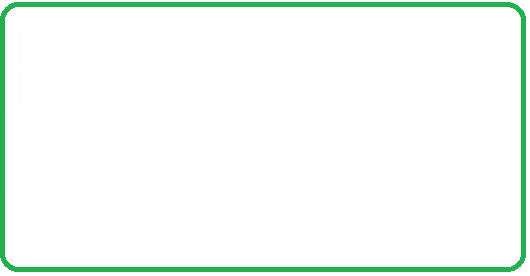
Вычисления, преобразования
Пример 1: Вычислить, преобразовать выражения, содержащие числовые радикалы:
1) $\sqrt{729}=27$
- потому, что $27$ именно то единственное положительное число, чей квадрат равен $729$;
2) $\sqrt{75}=\sqrt{3\cdot25}=\sqrt{3}\cdot\sqrt{25}=5\sqrt{3}$
- под корнем разложили на множители, увидели полный квадрат числа, извлекли;
3) $\sqrt{2^2\cdot3\cdot7^2\cdot6}=2\cdot7\cdot\sqrt{3\cdot3\cdot2}=2\cdot7\cdot3\cdot\sqrt{2}=42\sqrt{2}$
- вынос корня по частям от множителей - полных квадратов; Числа без квадратов "выходят" вперед.
4) $\frac{2}{\sqrt{3}}=\frac{2\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{2\sqrt{3}}{3}$
- умножили числитель и знаменатель на радикал, дробь не изменилась. используем $\sqrt{3}\cdot\sqrt{3}=3$;
5) $\sqrt{48}\cdot\sqrt{12}\cdot\sqrt{75}=\sqrt{48\cdot12\cdot75}=\sqrt{8\cdot6\cdot2\cdot6\cdot3\cdot25}=6\cdot5\cdot\sqrt{16\cdot3}=120\sqrt{3}$
- в конце вынос квадрата за знак; "если внутри квадрата два одинаковых множителя, из двух выносим один вперед".
6) $\frac{1}{\sqrt{3}-2}=\frac{1\cdot\left(\sqrt{3}+2\right)}{\left(\sqrt{3}-2\right)\cdot\left(\sqrt{3}+2\right)}=\frac{\sqrt{3}+2}{3-2^2}=-\sqrt{3}-2$
- избавили знаменатель от радикала, умножили на сопряженное и числитель, и знаменатель... упростили разность квадратов;
7) $\sqrt{0.81}=\sqrt{\frac{81}{100}}=\frac{\sqrt{81}}{\sqrt{100}}=\frac{9}{10}=0.9$
- десятичное число превратили в дробное , использовали свойство радикала от деления;
8) $\sqrt{\frac{64}{225}}=\frac{\sqrt{64}}{\sqrt{225}}=\frac{8}{15}$
- свойство радикала от деления. нашли дробь, квадрат которой будет подрадикальной дробью.
Полезные Навыки работы с радикалами:
- "Вынос квадрата за радикал" - если внутри радикала есть множитель - квадрат числа, то само число выносится вперед радикала.
- Если внутри радикала есть два одинаковых множителя (квадрат?), то множителем впереди радикала выносим один из них.
- Если в знаменателе дроби множителем является число с радикалом, то "для избавления" умножаем и числитель и знаменатель на радикал.
- Если в знаменателе сложный радикал (сумма, разность), то "для избавления" умножаем и числитель и знаменатель на сопряженное!
- Примечание: сопряженным к сумме называется разность, и наоборот. Например, сопряженные $a+\sqrt{b}$ и $a-\sqrt{b}$
Упрощения выражений с радикалами
Пример 2: Упростить радикальные выражения, используя свойства, формулы:
1) $\sqrt{5a}-\frac{1}{4}\sqrt{80a}+20\sqrt{0,05a}=\sqrt{5a}-\frac{1}{4}\sqrt{16\cdot5a}+20\sqrt{\frac{5}{100}\cdot a}=\sqrt{5a}-\frac{1}{4}\cdot4\cdot\sqrt{5a}+20\cdot\frac{1}{10}\cdot\sqrt{5\cdot a}=2\sqrt{5a}$
- разложение на множители под радикалом , вынос полного квадрата, группирование подобных $\sqrt{5a}$;
2) $3\sqrt{5}-\sqrt{20}+\sqrt{80}=3\sqrt{5}-\sqrt{4\cdot 5}+\sqrt{16\cdot 5}=3\sqrt{5}-2\sqrt{5}+4\sqrt{5}=\left(3-2+4\right)\cdot \sqrt{5}=5\sqrt{5}$
- вынос квадратного множителя из-под радикала, группирование подобных ;
3) $\sqrt{5b}-2\sqrt{20b}-3\sqrt{80b}=\sqrt{5b}-2\cdot2\cdot\sqrt{5b}-3\cdot4\cdot\sqrt{5b}=\left(1-4-12\right)\cdot\sqrt{5b}=-15\sqrt{5b}$
- частичный вынос за радикал, группирование подобных ;
4) $\left(5\sqrt{x}-2\sqrt{3y}\right)\left(3\sqrt{x}+\sqrt{3y}\right)=15x+5\sqrt{3xy}-6\sqrt{3xy}-2\cdot3y=15x-\sqrt{3xy}-6y$
- отрытие скобок, умножение радикалов, группирование подобных.
5) $\left(\sqrt{x}-\sqrt{2y}\right)\cdot\sqrt{2xy}=\sqrt{x}\cdot\sqrt{2xy}-\sqrt{2y}\cdot\sqrt{2xy}=\sqrt{x}\cdot\sqrt{x}\cdot\sqrt{2y}-\sqrt{2y}\cdot\sqrt{2y}\cdot\sqrt{x}=x\sqrt{2y}-2y\sqrt{x}$
- открытие скобок, умножение радикалов, свойство произведения $\sqrt{a\cdot b\cdot c\cdot x}=\sqrt{a}\cdot\sqrt{b}\cdot\sqrt{c}\cdot\sqrt{x}$ ;
6) $\left(3\sqrt{m}-4\sqrt{2n}\right)\left(3\sqrt{m}+4\sqrt{2n}\right)=\left(3\sqrt{m}\right)^2-\left(4\sqrt{2n}\right)^2=3^2\cdot m-16\cdot2n=9m-32n$
- формула разности квадратов, свойство $\left(a\sqrt{x}\right)^2=a\sqrt{x}\cdot a\sqrt{x}=a^2x$ ; $\left(5\sqrt{3y}\right)^2=25\cdot\left(\sqrt{3y}\right)^2$
7) $\left(2\sqrt{5}-7\sqrt{2}\right)\left(3\sqrt{2}+4\sqrt{5}\right)=2\sqrt{5}\cdot3\sqrt{2}+2\cdot5\cdot4-7\cdot2\cdot3-7\sqrt{2}\cdot4\sqrt{5}=6\sqrt{10}+40-42-28\sqrt{10}=-2-22\sqrt{10}$
- ф-ла разности квадратов, $7\sqrt{2}\cdot3\sqrt{2}=7\cdot3\cdot\sqrt{2}\cdot\sqrt{2}$ , группирование $17\sqrt{a}-7\sqrt{a}=10\sqrt{a}$;
8) $\left(3\sqrt{a}-\sqrt{c}\right)^2=\left(3\sqrt{a}\right)^2-2\cdot3\sqrt{a}\cdot\sqrt{c}+\left(\sqrt{c}\right)^2=9a-6\sqrt{ac}+c$
- применили формулу сокращенного умножения.
 пробел
пробел

Интерактивная доска:
Упражнения:
