Иррациональные числа, приближенные значения
- Дробные числа, или рациональные в десятичной записи имеют вид конечной или бесконечной периодической дроби.
- Любая обыкновенная дробь, у которой множителями знаменателя являются лишь $2$ или $5$ - имеет конечную десятичную запись.
- ... любая другая дробь, не с таким знаменателем, имеет бесконечную периодическую форму. И, наоборот.
- Число $\sqrt{2}$ не может быть никаким рациональным - "отношением двух", "делением двух целых".
- $N$ - множество натуральных чисел: Числа $1,2,3,4,5$ .... $103,104,105$ называются натуральными числами.
- $Z$ - множество целых чисел: .... $-4,-3,-2,-1, 0,1,2,3,4,5$ ..... все натуральные, ноль и еще отрицательные натуральные.
- $Q$ - множество рациональных чисел: целые + все обыкновенные дроби. Все конечные или периодические здесь!

Иррациональным числом называется число, у которого в десятичной записи бесконечная непериодическая дробь.
- $-\sqrt{6}$, $\sqrt{2,3}$, $3+\sqrt{2}$, $\pi$ $4\pi-2,5$ - иррациональные числа.
- $R$ - множество всех действительных чисел - все рациональные и иррациональные числа.
- Множество $R$ "плотное": между любыми двумя рациональными есть хоть одно иррациональное и хоть одно рациональное.
- Также, между иррациональными есть хоть одно рациональное и хоть одно иррациональное. "Все плотно!"

Пример 1 : Между какими соседними целыми находится число с радикалом
-
.... $\sqrt{7} ?$ Т.к $2^2=4$ меньше $<7<$ меньше $3^2=9$ , то Ответ: $2<\sqrt{7}<3$
-
.... $\sqrt{34} ?$ Т.к $5^2=25$ меньше $<34<$ меньше $6^2=36$ , то Ответ: $5<\sqrt{34}<6$
-
.... $\sqrt{407} ?$ Т.к $20^2=400$ меньше $<407<$ $21^2=441$ , то Ответ: $20<\sqrt{407}<21$
Суть: Находим ближайший "квадрат чего-либо" менее, чем наше число. И чтоб квадрат "следующего" было больше ...
Пример 2 : Найти приближенные значения чисел с радикалами
-
.... $\sqrt{3}\approx ?$ Легче узнать приближенно $\sqrt{300}\approx 17$ и поделить на $10$. Ответ: $\sqrt{3}\approx 1,7$
-
.... $\sqrt{17}\approx ?$ Легче узнать приближенно $\sqrt{1700}\approx 42$ и поделить на $10$. Ответ: $\sqrt{17}\approx 4,2$
-
.... $3\sqrt{7}-\sqrt{11}\approx ?$ $\sqrt{7}\approx 2,7$ $\sqrt{11}\approx 3,3$ $3\cdot2,7-3,3=4,8$ Ответ: $3\sqrt{7}-\sqrt{11}\approx 4,8$
Сравнение чисел, содержащих радикалы
- Сравнить, значит узнать что больше, что меньше. Что на числовой оси левее, а что правее - значит больше.
- Чтоб сравнить числа, иногда достаточно сравнить их приближенные значения ... станет ясно, что больше.
- Иногда полезно сравнить их квадраты и, в зависимости от знаков, сделать выводы о сравнениях ...
- Иногда полезно оба сравниваемых числа умножить на один и тот же множитель, ( на $2$ ? $\sqrt{3}$ ? $100$ ?) и сравнить полученные числа
Пример 3 : Сравнить числа $\sqrt{26}$ и $5,1$
- Сравним квадраты этих положительных чисел - "чей квадрат больше, тот и больше"
- $\left(\sqrt{26}\right)^2=26$ $5,1^2=26,01$ вывод, Ответ: $\sqrt{26}<5,1$
Пример 4 : Сравнить числа $\sqrt{5}-7$ и $-3-\sqrt{2}$
- Вычислим приближенно число: $\sqrt{5}-7\approx 2,3-7=-4,7$
- Вычислим приближенно число: $-3-\sqrt{2}\approx -3-1,4=-4,4$
- Сравним приближенные значения: т.к. $-4,7<-4,4$ то делаем вывод, Ответ: $\sqrt{5}-7<-3-\sqrt{2}$
Пример 5 : Сравнить числа $-4\sqrt{3}$ и $-3\sqrt{5}$
- Сравним квадраты положительных чисел $4\sqrt{3}$ и $3\sqrt{5}$- "чей квадрат больше, тот и больше"
- $\left(4\sqrt{3}\right)^2=48$ $(3\sqrt{5})^2=45$ вывод : Ответ: $4\sqrt{3}>3\sqrt{5}$
- Но их противоположные отрицательные наоборот: $-4\sqrt{3}<-3\sqrt{5}$ "Чем левее, тем меньше".

Сравнение Иррациональных Чисел
Пример 6: Сравнить числа $2\sqrt{11}$ и $3\sqrt{5}$
- "Сравнить числа" - значит доказать или опровергнуть составленное с ними неравенство.
- Предположим , что первое число больше второго. Это неравенство упростим до "наглядности":
- $2\sqrt{11} > 3\sqrt{5}$ $\Leftrightarrow$ $\left(2\sqrt{11}\right)^2 > \left(3\sqrt{5}\right)^2$ $\Leftrightarrow$ $4\cdot11 > 9\cdot5$ $\Leftrightarrow$ $44 > 45$ , это неверно ,
- а значит и наша неверна $\Rightarrow$ Ответ : $2\sqrt{11} < 3\sqrt{5}$
Правило сравнения:
- составить из сравниваемых чисел гипотетическое, предположительное неравенство;
- путем эквивалентных преобразований доказать его или опровергнуть ;
- если последнее неравенство в цепочке преобразований верно/ложно $\Leftrightarrow$ гипотетическое неравенство верно/ложно.
Пример 7: Сравнить числа $-\frac{9-\sqrt{12}}{4}$ и $-\frac{11}{8}$ .
- Допустим гипотезу $-\frac{9-\sqrt{12}}{4} > -\frac{11}{8}$ . Если бы это было верно, тогда :
- $\frac{9-\sqrt{12}}{4} < \frac{11}{8}$ $\Leftrightarrow$ $2\left(9-\sqrt{12}\right) < 11$ $\Leftrightarrow$ $18-11 < 2\sqrt{12}$ $\Leftrightarrow$ $7^2 < \left(2\sqrt{12}\right)^2$ $\Leftrightarrow$ $49 < 4\cdot12$ .
- Но! последнее очевидно ложно $\Rightarrow$ вывод: наше допущение надо поменять на противоположное $\Rightarrow$
- Ответ: $-\frac{9-\sqrt{12}}{4}$ < $-\frac{11}{8}$.
Пример 8: Расположить список чисел $\frac{\pi}{5}$ $\frac{\sqrt{26}-\sqrt{15}}{2}$ $\frac{\sqrt{3}}{\pi}$ $\frac{\sqrt{6}}{4}$ в порядке возрастания
- $\pi$ - это число, хоть и обозначается буквой. Оно всегда $\pi\approx 3,1415625....$ - иррациональное. Дает длину окружности.
- Найдем приближенные значения чисел из нашего списка. Вычислим приближенно шаг за шагом:
- $\frac{\pi}{5}\approx \frac{3,14}{5} \approx 0,63$ $\frac{\sqrt{6}}{4}\approx\frac{2,5}{4}\approx 0,62$
- $\frac{\sqrt{26}-\sqrt{15}}{2}\approx\frac{5,1-3,9}{2}\approx 0,6$ $\frac{\sqrt{3}}{\pi}\approx \frac{1,7}{3,14}\approx 0,55$
- Очевидно, получился такой порядок слева - направо Ответ: $\frac{\sqrt{3}}{\pi}<\frac{\sqrt{26}-\sqrt{15}}{2}<\frac{\sqrt{6}}{4}<\frac{\pi}{5}\approx \frac{3,14}{5}$

Пример 9: На числовых осях отмечены точки с буквами. Каковы числовые значения этих букв, если известно, что они выбраны из списка чисел, указанных на картинках у числовых осей.
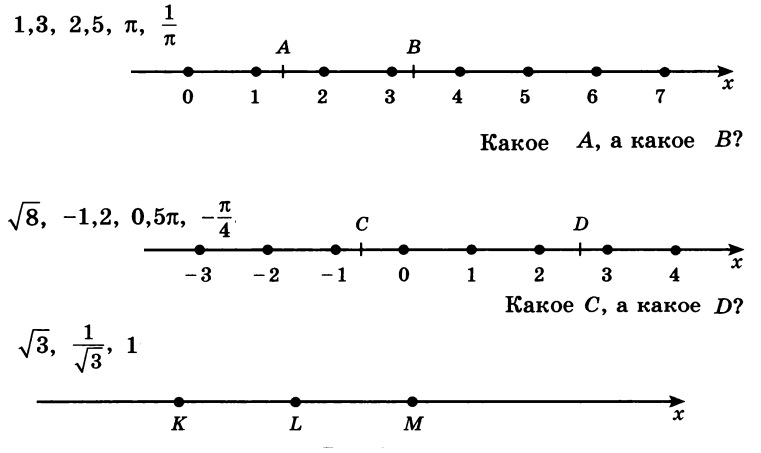
- Видно, что число $A$ находится между $1$ и $2$. Какое из предложенных чисел попадает туда же?
- Точка $С$ левее нуля, ближе к $-1$. Какое число могло быть там?
- $K$ - самое меньшее, $L$ среднее, $M$ - правое. А как с порядком предложенных чисел?
Интерактивная Доска:
Упражнения: