Функция $y=f\left(x\right)$ - это правило, по которому $x$ - аргументам соответствуют $y$ - значения.
- $x$ называется аргументом функции.
- $y$ переменная - значение функции при определенном аргументе.
- $f\left(x\right)$ - Правило, или закон функции - по которому вычисляются значения функции.
- Пример: $f\left(x\right)=\sqrt{x+10}$ ... то аргументу $x=6$ соответствует $y=4$ потому как $f\left(3\right)=\sqrt{6+10}=4$
- $f\left(x\right)=\sqrt{x+10}$ ... то аргументу $x=-7$ соответствует $y=\sqrt{3}$ т.к $f\left(-7\right)=\sqrt{-7+10}\approx1,7$
График функции - кривая, изображающая значения функции при различных аргументах.
Таблица значений функции - список соответствий $\left(x;y\right)$, вычисленных для нескольких $x$ - аргументов.
- Если при каком-то аргументе $x=-1$ значением функции будет $y=3$, то точка с координатами $\left(-1;3\right)$ лежит на графике.
- Если точка $\left(15;5\right)$ лежит на графике, то: аргументу $x=15$ соответствует значение $y=5$
- Если точка $\left(4;6\right)$ не лежит на графике, то аргументу $x=4$ Не соответствует значение $y=6$
- Если точка $\left(4;6\right)$ по вертикали ниже точки графика для $x=4$, то: $6<f\left(4\right)$ - меньше!
- График строится по таблице значений функций: вычисляются точные или приближенные значения функции при разных $x$ - аргументах.
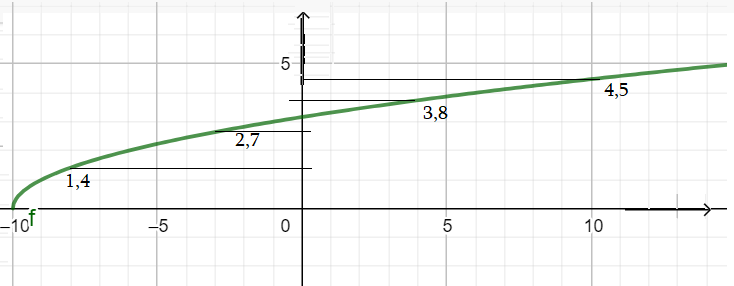
- Пример: $f\left(-6\right)=2$ $f\left(-9\right)=1$ $f\left(-7\right)=\sqrt{3}\approx1,7$ $f\left(-3\right)\approx 2,7$ $f\left(0\right)\approx 3,2$ $f\left(4\right)\approx 3,8$ $f\left(6\right)=4$
- Составляется список точек графика, таблица значений: $\left(-6;2\right)$ $\left(-9;1\right)$ $\left(-7;1,7\right)$ $\left(-3;2,7\right)$ $\left(0;3,2\right)$ $\left(4;3,8\right)$
Пример 1: Построить график функции $y=\sqrt{x+10}$
- У нас есть список точек. Нанесем точки с этими координатами. Проведем через них кривую - получим график.
- Вычислим еще значения: при $x=-10$, получим $y=0$ при $x=0$, получим $y\approx1,7$
- Область определения функции - луч $[ -10 ; + ∞)$. - все числа больше -10.
Вопросы наизусть: Смотри на график и ответь: 1) В какой точке пересекается с $x$ - осью? а в какой с $y$ ? 2) В какой точке функция принимает большее значение в $x=3$ или $x=4$ 3) верно ли утверждение: чем больше $x$ тем большее значение у функции? 4) Функция возрастает или убывает?
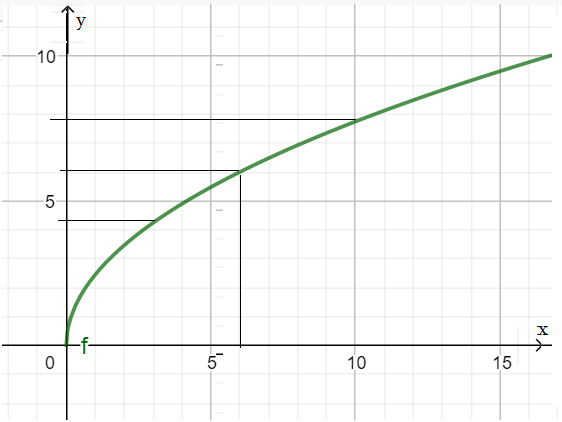
Пример 2: Построить график функции $y=\sqrt{6x}$
- Вычислим несколько значений: $f\left(0\right)=0$ $f\left(1\right)=\sqrt{6}\approx2,5$ $f\left(2\right)=\sqrt{12}\approx3,5$ $f\left(3\right)=\sqrt{18}\approx4,3$
- $f\left(7\right)=\sqrt{42}\approx6,5$ $f\left(8\right)=\sqrt{48}\approx7,0$ $f\left(10\right)=\sqrt{60}\approx7,8$
- Получили список точек, их координат. Таблица значений. Отметим точки на координатной плоскости. Проведем график.
- Область определения - все неотрицательные числа. Функция возрастает . Область значений - неотрицательные числа.
Пример 3: Построить график функции $y=\sqrt{x}$
Вычислим точные или приближенные значения $\sqrt{x}$ при нескольких числовых $x$ - аргументах. Составим таблицу значений. Составим список точек $(?;?)$ , которые должны оказаться на графике. Отметим эти точки на координатной плоскости. Проведем плавную линию через эти точки. Получим график.

Cвойства функции $y=\sqrt{x}$ (одна ветвь лежащей параболы в первом координатном угле) .
- Свойство 1: областью определения функции является промежуток $[ 0 ; + ∞)$..
- Свойство 2: Множеством значений функции является промежуток $[ 0 ; + ∞)$.
- Свойство 3: Значение функции $у=0$ является наименьшим, а наибольшего значения функция не имеет.
- Свойство 4: График функции пересекается с осями в единственной точке - $(0;0)$.
- Свойство 5: Функция монотонно возрастает на области определения.
- Свойство 6: Функция принимает положительные значения на промежутке , график расположен в I координатном угле..
Наблюдения: Выражение √x определено лишь при x ≥0 . Если аргумент возрастает от 0 до бесконечности, функция возрастает от 0 до бесконечности. Множество значений функции – 0 и положительные числа. На оси $y$ для этой функции нет самого большого положительного числа. Функция имеет наименьшее значение.
Cравнение графиков со сдвинутыми х - аргументом или у - значением
Как отличаются графики $y=\sqrt{x+1}$ , $y=\sqrt{x-1}$ , $y=\sqrt{x}+2$ , $y=\sqrt{x}-1$ от графика $y=\sqrt{x}$
Отличаются сдвигами $y=\sqrt{x}$: вправо на +1 ? влево на -1 ? вверх на +? вниз на -1?

Решение уравнений с помощью графиков
Визуальное решение уравнения: построим график левой части уравнения. Он покажет какие значения принимает левая часть при разных значениях неизвестного. Построим фото правой части, его график покажет какие значения принимает в разных точках. Для поиска корня уравнения нам нужно "поймать" ту точку, в котором левая и правая части выравниваются. Значит, надо искать пересечение этих графиков: для такого х - неизвестного обе части уравнения будут равны. И так: точки пересечения этих графиков дадут нам на корни уравнения - х - координата этих точек удовлетворяет уравнению.
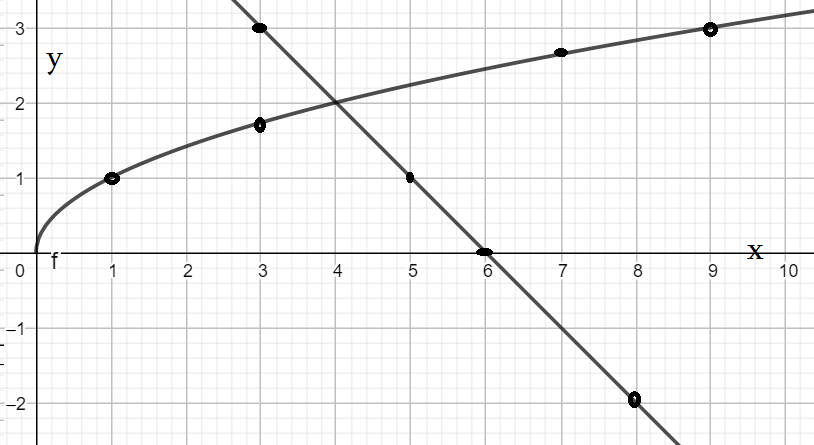
Пример 4: Решите графически уравнение . $\sqrt{x}=6-x$
- Построим графики функций $y=\sqrt{x}$ и $y=6-x$ в одной координатной плоскости.
- Вычислим значения функции из левой части уравнения: $f\left(x\right)=\sqrt{x}$ в нескольких точках:
- $f\left(1\right)=1$ $f\left(3\right)\approx1,7$ $f\left(7\right)\approx2,7$ $f\left(9\right)=3$ $f\left(12\right)\approx3,5$.
- Составим список точек: $(1;1)$ $(3;1,7)$ $(7;2,7)$ $(9;3)$ $(12;3,5)$ . По точкам проведем график.
- Составим список точек для функции $y=6-x$: $(0;6)$ $(1;5)$ $(3;3)$ $(6;0)$ $(8;-2)$ . Проведем график - линию.
- Где, в какой точке эти графики пересекаются? Визуально видно, что в точке $(4;2)$. Что это значит?
- При аргументе $x=4$ обе функции принимают одно и тоже значение. Значит, равны $\sqrt{x}=6-x$. Ответ: $x=4$
- Вывод: Для нахождения решения уравнения надо "увидеть" точку пересечения графиков левой и правой частей.
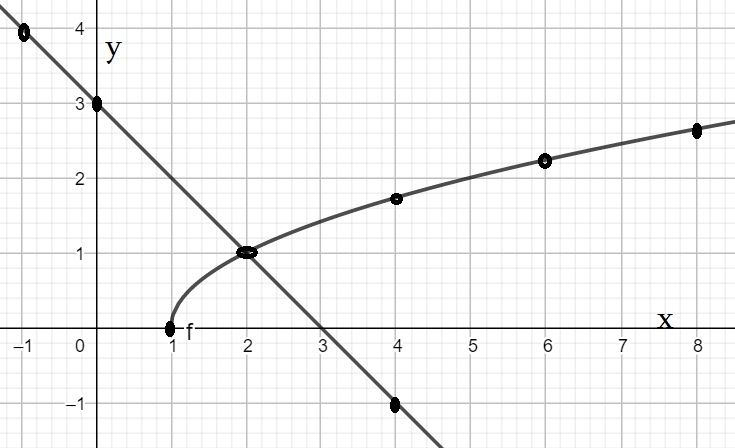
Пример 5: Решите графически уравнение . $\sqrt{x-1}=3-x$
- Решением уравнения будет то число $x$, при котором пересекаются графики функций $y=\sqrt{x-1}$ и $y=3-x$
- Точки графика функции $y=\sqrt{x-1}$: $(1;0)$ $(4;1,7)$ $(6;2,3)$ $(8;2,7)$ $(10;3)$ .
- Точки графика линейной функции $y=3-x$: $(-1;4)$ $(0;3)$ $(4;-1)$ $(7;-4)$ $(10;-7)$ .
- Видно, что графики пересекаются в точке с координатами $(2;1)$ . Значит, при $x=2$ обе функции имеют значение $1$.
- Это означает, что и левая и правая части в этой точке равны ... т.е. это решение уравнения Ответ: $x=2$.
Упражнения:
