Одночлен. Приведение к стандартному виду.

Учебник
Алгебра, 7 класс
IMG_0454.JPG

Учитель

Темур Кварацхелия
Одночлен. Приведение к стандартному виду.

Одночлен    -    это   такое   алгебраическое   выражение,   которое   состоит   из   произведения   степеней   и   чисел.

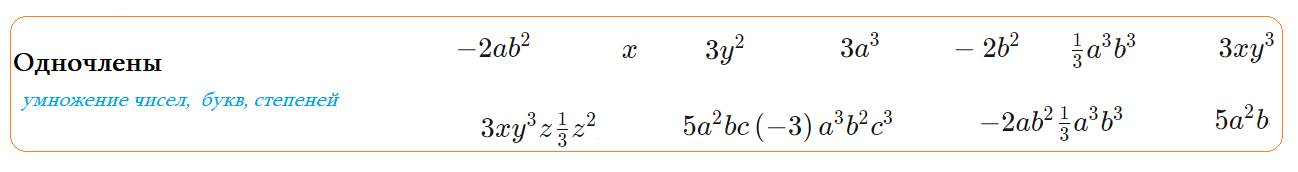
Эти выражения   не   являются   одночленами:     $x+y$;     $3a^3-2b^2$;     $\frac{2}{a}$;     $3y^2+3$;     в   каждом 2   Одночлена.

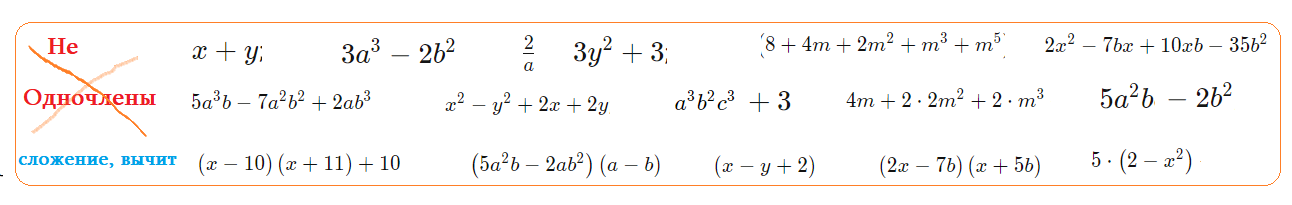
Стандартный   вид   одночлена        один числовой множитель, буква не повторяется.

Правило   приведения   одночлена   к   стандартному   виду:

  • одночлен - это перемножение чисел, букв, степеней букв. Возможно со знаками и скобками;

  • пока идет умножения чего-либо - это все один одночлен. Одночлен состоит из множителей;

  • Если среди множителей несколько числовых, то это "нестандартный вид": надо перемножить числа;

  • Если среди множителей одна и та же буква (или ее степень) в разных местах, то это "нестандартный вид";

  • перемножить   все   числовые   множители,   получить   коэффициент   одночлена;

  • поставить   полученный   коэффициент   на   первое   место;

  • перемножить   все   степени с одинаковыми буквами-переменными, получить единную степень каждого переменного по отдельности;

  • полученный коэффициент поставить в начало, а затем буквенную   часть в виде умножения букв или их степеней;

Пример 1:                  Привести одночлен к стандартному виду                 $-2ab^2\frac{1}{3}a^3b^3$

здесь:   два   коэффициента   –   $\left(-2\right)$   и   $\frac{1}{3}$,   переменные   $a$   и   $b$   встречаются   по   два   раза   –   $a$   и    $a^3$;   $b^2$   и   $b^3$.

сначала   нужно   перемножить   все   числовые   множители:     $-2\cdot\frac{1}{3}=-\frac{2}{3}$;    получили     коэффициент   одночлена.

далее:   перемножим   степени,   при   умножении   показатели   степени   складываются:   $a\cdot a^3=a^4$;   перемножим

степени   $b$:      $b^2\cdot b^3=b^5$;      в   итоге   получаем:      $-2ab^2\frac{1}{3}a^3b^3=-\frac{2}{3}a^4b^5$      -   стандартный   вид   исходного   одночлена,

$-\frac{2}{3}$   -   это   коэффициент,   $a$     –   это   буквенная   часть.               ответ:                $-2ab^2\frac{1}{3}a^3b^3=-\frac{2}{3}a^4b^5$

Пример 2:                  Привести одночлен к стандартному виду                     $5a^2bc\left(-3\right)a^3b^2c^3$

перемножим численные множители:   $5\cdot\left(-3\right)=-15$    –     получим   коэффициент   заданного   одночлена;

перемножим между собой степени:    $a^2\cdot a^3=a^5$;     $b\cdot b^2=b^3$ ;    $c\cdot c^3=c^4$.          ответ:          $5a^2bc\left(-3\right)a^3b^2c^3=-15a^5b^3c^4$

Пример 3:                  Привести одночлен к стандартному виду                     $3xy^3z\frac{1}{3}z^2$;

перемножить числовые множители:      $3\cdot\frac{1}{3}=1$   –     получим   коэффициент   заданного   одночлена;

перемножим   между   собой   степени:    переменные    $x$    и    $y$   встречаются   только   по   разу,   поэтому   их   перемножить

ни   с   чем   нельзя,   степень    $z$   перемножается:   $z\cdot z^2=z^3$;                        ответ:          $3xy^3z\frac{1}{3}z^2=xy^3z^3$;

Пример 4:                  Привести одночлен к стандартному виду                               $-3ya^2b^3c^k\frac{1}{3}ya^3bc$

перемножим   численные   множители:      $-3\cdot\frac{1}{3}=-1$    -   коэффициент   одночлена   равен   «$-1$»

перемножим   между   собой   степени:   $y\cdot y=y^2$ ;     $a^2\cdot a^3=a^5$ ;      $b^3\cdot b=b^4$ ;      $c^k\cdot c=c^{k+1}$ ;   

ответ:              $-3ya^2b^3c^k\frac{1}{3}ya^3bc=-y^2a^5b^4c^{k+1}$

Пример 5:                  Привести одночлены к стандартному виду

$2xy\cdot3x^2=2\cdot3\cdot x^{1+2}y=6x^3y$ ;                      $2,5x^3\cdot2y=2,5\cdot2\cdot x^3\cdot y=5x^3y$ ;

$1,5y^3\cdot3x^2=1,5\cdot3\cdot x^2\cdot y^3=4,5x^2y^3$ ;            $3xy^2\cdot5xy=3\cdot5\cdot x^{1+1}\cdot y^{2+1}=15x^2y^3$

Интерактивная Доска:

Упражнения, примеры:

Правило   умножения   одночлена   на   одночлен:

при   умножении   одночлена   на   одночлен   нужно   перемножить коэффициенты   отдельно, буквенные   части   отдельно   –   для   каждой букви "собрать" все его степени в единую степень.

  • единая степень при одинаковом основании "собирается" по формуле        $a^m\cdot a^n=a^{m+n}$.

  • если у одночлена нет числового коэфициента, то подразумевается $1$. Если знак "минус", то $-1$

Пример 1:                  Выполнить   умножение

1)   $5a\cdot2b=10ab$ ;        
2)   $3x\cdot2y\cdot3xy=18x^2y^2$ ;       
3)   $4a^2b^5c^4\cdot3ab^2c^3=12a^{2+1}b^{5+2}c^{4+3}=12a^3b^7c^7$ ;
4)   $3x^3y^2\cdot5x^2=3\cdot5\cdot x^{3+2}y^2=15x^5y^2$;         
5)   $3x^3yz^3\cdot\frac{1}{6}x^2zk^2\cdot x^3y^2=3\cdot\frac{1}{6}\cdot x^{3+2+3}\cdot y^{1+2}\cdot z^{3+1}\cdot k^2=\frac{1}{2}x^8y^3z^4k^2$

Правило   возведения   одночлена   в   степень:    

чтобы   возвести   одночлен   в   степень,   нужно   его   коэффициент   возвести в   эту   степень, а   также   каждую   переменную   возвести   в   степень. Использовать формулу $\left(a^n\right)^k=a^{n\cdot k}$ .

Пример 2:                  Возвести   одночлен   в   степень.

1)   $\left(2x^3z\right)^2=4x^6z^2$ ;                         
2)    $\left(3n^2m\right)^3=27n^6m^3$ ;          
3)   $\left(-\frac{1}{2}ab^3\right)^4=\frac{1}{16}a^4b^{12}$ ;     
4)   $\left(-\frac{1}{3}xyz\right)^3=-\frac{1}{27}x^3y^3z^3$ ;          
5)   $\left(-4a^2b^2\right)^2=16a^4b^4$ ;         
6)   $\left(-7a^4b^4\right)^0=1$ ,   при любом основании степень $0$ дает значение $1$ !?.

Пример 3:        В   равенство     * $2x^3=6x^4$   вместо   знака   «*»   поставить   нужное.

Коэффициент   в   левой   части   пока   равен   двум,   а   в   правой   –   шести,   значит,   в   левой   части   не   хватает   тройки;

переменная   $x$   в   левой   части   стоит   в третьей   степени,   а   в   правой   в   четвертой,   значит   левую   часть   нужно

умножить   на   $x$   в   первой   степени:      $3x2x^3=6x^4$ ;      $6x^4=6x^4$

Пример 4:        Определить,   какой   одночлен   возвести   в   квадрат,   чтобы   получить   $36x^4$.

1) $36x^4$     Чтобы   получить   $36$,   нужно   $6$   возвести   в   квадрат,   то   есть   коэффициент   $6$.

Чтобы   получить   $x^4$, нужно     $x^2$      возвести   в   квадрат:

Значит, их произведение даст нужный результат:    $\left(6x^2\right)^2=36x^4$ ;

2) Еще пример, чей квадрат:              $81y^8=\left(9y^4\right)^2=\left(-9y^4\right)^2$ ;             

3) И еще                $\frac{1}{6}a^5b^4c^3\cdot\left(-6\right)ab^3c=-a^6b^7c^4$

Операции   с   одночленами,   упрощения

Пример 5:        Умножить   одночлены     $\frac{2}{3}xy^3\cdot\left(-0,6\right)x^4y$.

Перемножим числовые коэффициенты     $\frac{2}{3}$   и    $-0,6$

Буква $x$ встречается множителем два раза - в 1-ой и 4-ой степени. "соберем" по сложению показателей.

Переменная $y$ тоже в двух местах. Соберем как единую степень:    $y$ в степени 3? 4? 5?.

Получаем:              $\frac{2}{3}xy^3\cdot\left(-0,6\right)x^4y=\frac{-0,6\cdot2}{3}x^{1+4}y^{3+1}=-0,4x^5y^4$.

Пример 6:        Упростить      $-16a^4b\cdot\left(\frac{1}{2}a^2b^3\right)^3$ .

Сначала   возведём   выражение   в   скобках   в   куб,   а   затем   применим   свойство   умножения   одночленов:

$-16a^4b\cdot\left(\frac{1}{2}a^2b^3\right)^3=-16a^4b\cdot\left(\frac{1}{2}\right)^3a^{2\cdot3}b^{3\cdot3}=-16a^4b\cdot\frac{1}{8}a^6b^9=-\frac{16}{8}a^{4+6}b^{1+9}=-2a^{10}b^{10}$ .

Упражнения, примеры: