Сокращение дробей
правило: Если числитель и знаменатель дроби одновременно умножить на одно и то же число, дробь не изменится.
Сокращение дроби (деление числителя и знаменателя на одно и то же число) не меняет дробь, значение остается то же.
следующие дроби все равные, суть одна и та же: $\frac{2}{3}=\frac{10}{15}=\frac{4}{6}=\frac{12}{18}=\frac{20}{30}=\frac{16}{24}=\frac{200}{300}$
// две третьих торта то же самое, что и 12 кусков 18-х частей того же торта. Не больше, не меньше! $\frac{2}{3}=\frac{12}{18}$//
правило сокращения: найти число (или числа), на которое делится и числитель и знаменатель. Поделить их на такое число.
Пример 1: цепочка сокращений $\frac{24}{360}=\frac{12}{180}=\frac{6}{90}=\frac{3}{45}=\frac{1}{15}$
Пример 2: $\frac{14\cdot9}{15\cdot7}=\frac{14\cdot3}{5\cdot7}=\frac{2\cdot3}{5\cdot1}=\frac{6}{5}=1\frac{1}{5}$
Приведение к другому знаменателю
Пример 3: приведем дробь $\frac{2}{7}$ к знаменателю $35$ .
число $35$ кратно $7$ , $35:7=5$ . Число $5$ будет для дроби Дополнительным множителем .
Умножим на 5 числитель и знаменатель дроби: $\frac{2}{7}=\frac{2\cdot5}{7\cdot5}=\frac{10}{35}$ <=> привели дробь к другому знаменателю и получили $\frac{10}{35}$ .
Число, на которое надо умножить знаменатель, чтобы получить новый знаменатель, называют дополнительным множителем.
При приведении дроби к другому знаменателю ее числитель и знаменатель умножают на дополнительный множитель.
Дроби: сложение, вычитание, сравнение.
правило: Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями, надо:
1) привести данные дроби к наименьшему общему знаменателю;
2) сравнить (сложить, вычесть) полученные дроби.
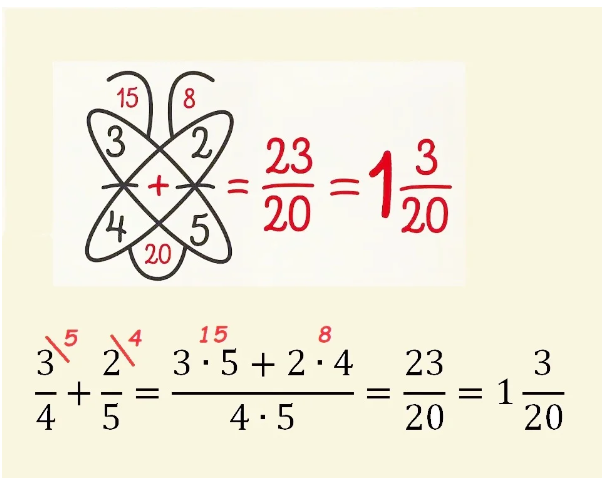
Пример 4: сложить $\frac{2}{3}$ и $\frac{3}{5}$ .
приведем дроби к наименьшему общему знаменателю $15$. Сложим $\frac{2}{3}+\frac{3}{5}=\frac{2\cdot5}{15}+\frac{3\cdot3}{15}=\frac{10}{15}+\frac{9}{15}=\frac{19}{15}=1\frac{4}{15}$
Пример 5: вычесть $\frac{2}{3}$ и $\frac{3}{5}$ .
$\frac{2}{3}-\frac{3}{5}=\frac{2\cdot5}{15}-\frac{3\cdot3}{15}=\frac{10}{15}-\frac{9}{15}=\frac{10-9}{15}=\frac{1}{15}$
Пример 6: сравнить $\frac{2}{3}$ и $\frac{3}{5}$ .
первая дробь равна$\frac{10}{15}$ , вторая $\frac{9}{15}$ . При одинаковых знаменателях у первой дроби числитель больше:
$\frac{10}{15} > \frac{9}{15}$ => $\frac{2}{3}$ > $\frac{3}{5}$ .
правило: привести дроби к наименьшему общему знаменателю - значит выполнить следующее:
1) найти Н.О.К их знаменателей.
2) найти дополнительный множитель для каждой дроби по-отдельности: = ( Н.О.К ) : (его знаменатель) !
3) вычислить числитель новой дроби: = (старый числитель) * (свой дополнительный множитель ) .
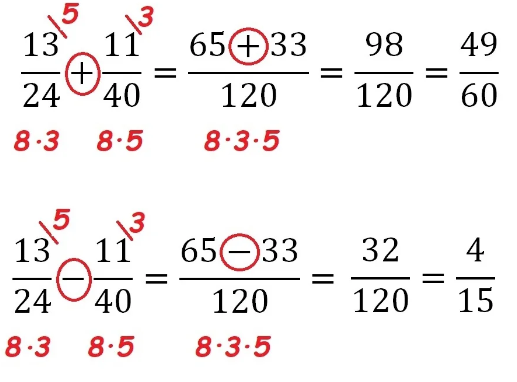
Умножение и деление дробей
правило: Чтобы умножить дробь на дробь, надо:
1) найти произведение числителей этих дробей и записать его числителем новой дроби ;
2) найти произведение знаменателей и записать его знаменателем новой дроби. Например: $\frac{3}{8}\cdot\frac{15}{17}=\frac{3\cdot15}{8\cdot17}=\frac{45}{136}$
Пример 7: умножение дробей $\frac{4}{7}\cdot\frac{14}{15}=\frac{4\cdot14}{7\cdot15}=\frac{4\cdot2}{1\cdot15}=\frac{8}{15}$
(написать произведение числителей и произведение знаменателей; произвести сокращения; выполнить умножение )
правило: Чтобы разделить одну дробь на другую, надо делимую дробь умножить на обратную делителю (перевернуть).
Например: $\frac{3}{8}:\frac{15}{17}=\frac{3}{8}\cdot\frac{17}{15}=\frac{3\cdot17}{8\cdot15}=\frac{51}{120}$
Пример 8: деление дробей $\frac{5}{9}:\frac{10}{21}=\frac{5}{9}\cdot\frac{21}{10}=\frac{5\cdot21}{9\cdot10}=\frac{1\cdot7}{3\cdot2}=\frac{7}{6}=1\frac{1}{6}$
( перевернуть делимую дробь; обозначить произведение числителей и произведение знаменателей;
произвести возможные сокращения; выполнить умножение; неправильную дробь превратить в смешанную .)
правило: Чтобы умножить или поделить целое и дробь: целое число надо превратить в дробь со знаменателем единица.
Поделить дробь на целое число - это значит, надо умножить дробь на дробь, обратную целому числу.
Пример 9: $\frac{12}{18}\cdot32=\frac{12}{18}\cdot\frac{32}{1}=\frac{2}{3}\cdot\frac{32}{1}=\frac{64}{3}$
Пример 10: $\frac{15}{16}:5=\frac{15}{16}\cdot\frac{1}{5}=\frac{15\cdot1}{16\cdot5}=\frac{3}{16}$
Пример 11: $5:\frac{15}{16}=\frac{5}{1}\cdot\frac{16}{15}=\frac{5\cdot16}{1\cdot15}=\frac{16}{3}=5\frac{1}{3}$

Упражнения для освоения урока:
Задание к уроку :
