Алгебраические выражения : числа, переменные, операции
Алгебраическое выражение состоит из чисел, букв - переменных, скобок и действий: сложения, вычитания, умножения, деления, знак дроби, возведения в степень.
Суть "алгебраического выражения" - задать правило , по которому при заданных числовых значениях входящих букв можно вычислить числовое значение этого выражения.
- Внимание: в алгебраическом выражении не может быть знака "=" или любого знака сравнения.
За алгебраическим выражением "прячется" бесконечное количество всевозможных чисел, значений которые получаются при замене букв на конкретные числовые значения. Мешок числовых значений.
Пример 1: Вычислить выражения $y^2-8y+7$ и $\left(y-7\right)\left(y-1\right)$ при разных значениях $y$
Для вычисления значений выражения надо подставить число вместо переменной и произвести вычисления. Полученный результат называется значением выражения с переменной при заданных числовых значениях этих переменных.
Алгоритм вычисления выражений:
- В начале строки напишем при каких значениях букв собираемся вычислять ... $a=5$ $b=-6$
- В форму выражения подставим вместо буквы её число ... тупо вынимаем букву и вставляем число.
- далее производим действия: умножения и деления чисел производятся раньше сложений и вычитаний.
- Скобку надо вычислить? вычисляй её содержимое. Скобка - это мешок, упаковка для числа.
- При возведении в квадрат, куб нужна внимательность. Что именно возводится и что получается.
$y=3$ $y^2-8y+7=3^2-8\cdot3+7=9-24+7=-8$ числовое значение $-8$
$y=3$ $\left(y-7\right)\left(y-1\right)=\left(3-7\right)\left(3-1\right)=-8$
$y=-3$ $y^2-8y+7=(-3)^2-8\cdot (-3)+7=9+24+7=40$ числовое значение $40$
$y=-3$ $\left(y-7\right)\left(y-1\right)=\left(-3-7\right)\left(-3-1\right)=40$
$y=\frac{2}{3}$ $y^2-8y+7=\left(\frac{2}{3}\right)^2-8\cdot \left(\frac{2}{3}\right)+7=\frac{4}{9}-\frac{16}{3}+7=\frac{4-48+63}{9}=\frac{19}{9}$
$y=\frac{2}{3}$ $\left(y-7\right)\left(y-1\right)=\left(\frac{2}{3}-7\right)\left(\frac{2}{3}-1\right)=\frac{-19}{3}\cdot \frac{-1}{3}=\frac{19}{9}$
Два алгебраических выражения могут различаться по форме, но быть равными, одинаковыми по сути:
Алгебраические выражения равные если числовые значения этих выражений совпадают при всех одних и тех же значениях букв: при вычислениях дают одинаковые результаты.
$y^2-8y+7=\left(y-7\right)\left(y-1\right)$ $3-2b=2-2b+1$ $(3-a)^2=a^2+9-6a$
Тождественные преобразования выражений - это цепочка нескольких выражений, связанных знаками "=". Каждые выражения в цепочке одинаковые по значениям, но различные по форме.
$\left(a-b\right)^2=\left(a-b\right)\left(a-b\right)=a\cdot a-a\cdot b-b\cdot a+b\cdot b=a^2-2ab+b^2$
- Квадрат числа (выражения) - умножить это число (выражение) на само себя.
$a^2=a\cdot a$ $(-7)^2=49$ $(3-a)^2=(3-a)\cdot (3-a)$ $(5x)^2=25\cdot x^2$
- Куб числа (выражения) - умножить это число (выражение) на само себя три раза.
$b^3=b\cdot b\cdot b$ $(-4)^3=-64$ $(3-2b)^3=(3-2b)\cdot (3-2b)\cdot (3-2b)$
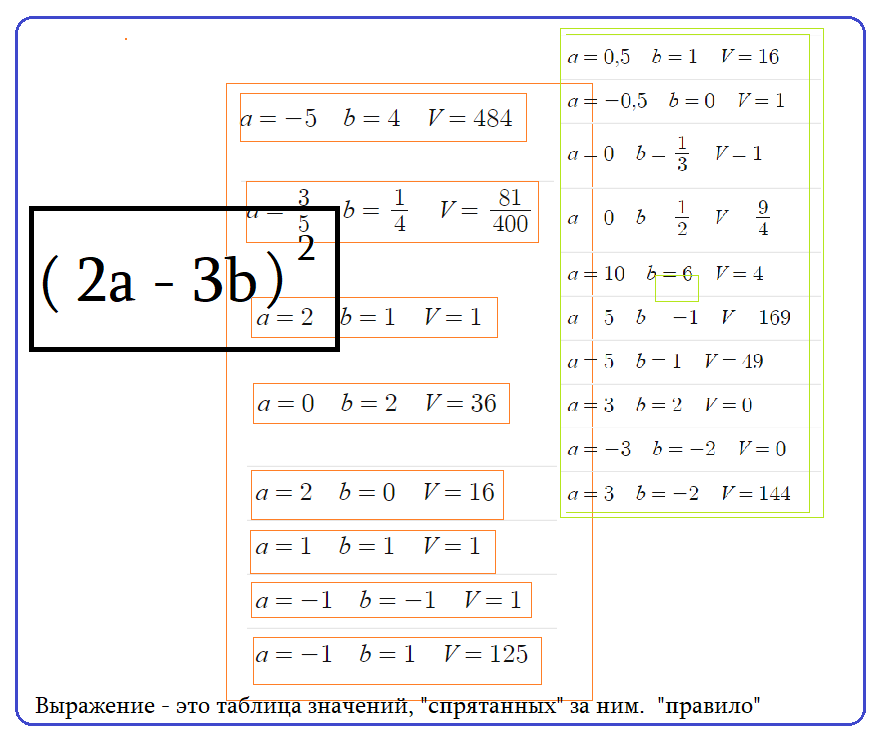
Пример 2: Вычислить выражение $(2a-3b)^2$ при разных значениях $a$ и $b$
$a=-5$ $b=4$ $(2a-3b)^2=(2\cdot (-5)-3\cdot 4)^2=(-22)^2=484$
$a=\frac{3}{5}$ $b=\frac{1}{4}$ $(2a-3b)^2=(2\cdot (\frac{3}{5})-3\cdot \frac{1}{4})^2=(\frac{6}{5}-\frac{3}{4})^2=(\frac{9}{20})^2=\frac{81}{400}$
Внимание: при подстановке вместо буквы отрицательного числа его надо заключить в скобки. Иначе могут быть ошибки ... будто бы вычитание.
Пример 3: Вычислить кубы чисел $5$, $-\frac{3}{4}$, $0,2$ . Еще $2\cdot x$
$5^3=5\cdot 5 \cdot 5=25\cdot 5=125$
$(-\frac{3}{4})^3=(-\frac{3}{4})\cdot (-\frac{3}{4})\cdot (-\frac{3}{4})=-\frac{27}{64}$
$0,2^3=0,2\cdot 0,2 \cdot 0,2=0,04\cdot 0,2=0,008$
$(2\cdot x)^3=(2\cdot x)\cdot (2\cdot x)\cdot (2\cdot x)=8\cdot x^3$

Интерактивная Доска:
Упражнения, примеры:
