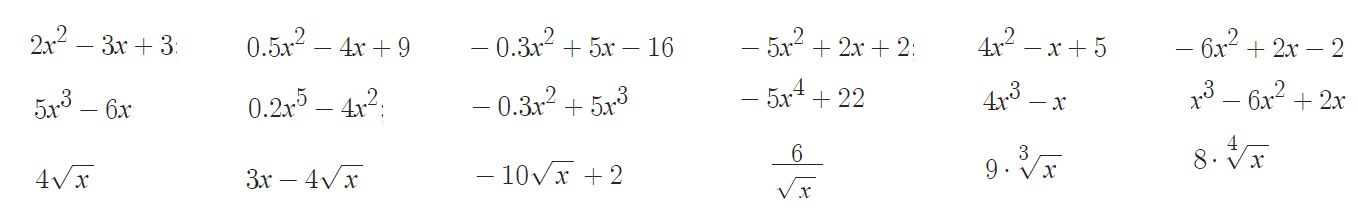- Функция - это правило отображения $x$ $\to$ $y$, т.е. аргумент функции $\to$ значение функции.
- Каждая функция имеет свою производную функцию. Т.е. есть функция $\left(f\left(x\right)\right)$ и есть ее производная $f'\left(x\right)$
- Производная функции показывает скорость изменения функции в точке, тангенс угла наклона его графика.
- Производная числа (т.е. функция всюду = числу) равна нулю. Число - постоянная функция никак не изменяется! Константа.
Calculus: Таблица и Правила Дифференцирования
Дифференцирование .... процесс нахождения-вычисления производной функции от какой-либо функции
Таблица Производных
-
Константа: $\left(C\right)'=0$ $\left(-13,5\right)'=0$ $\left(\sqrt{5}\right)'=0$
-
Степень: $\left(x^n\right)'=n\cdot x^{n-1}$ основание - переменная, показатель $n$ - число, любое
- примеры: $\left(x\right)'=1$ $\left(x^2\right)'=2x$ $\left(x^3\right)'=3x^2$ $\left(x^{-1}\right)'=-x^{-2}$ $\left(x^{-2}\right)'=-2\cdot x^{-3}$
- Корень как степень: $\left(\sqrt{x}\right)'=\left(x^{\frac{1}{2}}\right)'=\frac{1}{2}\cdot x^{-\frac{1}{2}}$ $\left(\sqrt[m]{x}\right)'=\left(x^{\frac{1}{m}}\right)'=\frac{1}{m}\cdot x^{\frac{1}{m}-1}$
- примеры: $\left(\sqrt{x}\right)'=\frac{1}{2\sqrt{x}}$ $\left(\sqrt[3]{x}\right)'=\left(x^{\frac{1}{3}}\right)'=\frac{1}{3}\cdot x^{-\frac{2}{3}}$
- тригонометрия: $\left(\sin x\right)'=\cos x$ $\left(\cos x\right)'=-\sin x$
- примеры: $\left(\tg x\right)'=\frac{1}{\cos^2x}$
- экспоненциальная $\left(e^x\right)'=e^x$
- примеры: $\left(5^x\right)'=5^x\cdot \ln 5$ показательная $\left(a^x\right)'=a^x\cdot \ln a$ , основание - число, показатель- переменная.
- Логарифмическая $\left(\ln x\right)'=\frac{1}{x}$
- примеры: $\left(\log _2x\right)'=\left(\frac{\ln x}{\ln 2}\right)'=\frac{1}{x\cdot \ln 2}$ $\left(\log _ax\right)'=\left(\frac{\ln x}{\ln a}\right)'=\frac{1}{x\cdot \ln a}$
Правила Дифференцирования
-
Числовой множитель выносится как коэффициент: $\left(7,1\cdot A\left(x\right)\right)'=7,1\cdot\left(A\left(x\right)\right)'$
-
производная суммы равна сумме производных: $\left(A-B+C\right)'=A'-B'+C'$
-
правило производной от умножения: $\left(A\cdot B\right)'=A'\cdot B + A\cdot B'$
-
правило производной от деления: $\left(\frac{A}{B}\right)'=\frac{A'\cdot B - A\cdot B'}{B^2}$
-
производная сложной функции : $\left(f\left(X\right)\right)'=f'\left(X\right)\cdot\left(X\right)'$
Задача 1: Найти производную от функции $f\left(x\right)=x^3-3x+2$ .
- $f'\left(x\right)=\left(f\left(x\right)\right)'=\left(x^3-3x+2\right)'$ производная суммы 3-х равен сумме производных каждого слагаемого
- решение: $\left(x^3-3x+2\right)'=\left(x^3\right)'+\left(-3x\right)'+\left(2\right)'=3x^2-3\cdot1+0=3x^2-3$
- Наша функция есть сумма 3-х слагаемых. Правило (сумма)' $\left(x^3-3x+2\right)'=\left(x^3\right)'+\left(-3x\right)'+\left(2\right)'$
- производная куба: $\left(x^3\right)'=3x^2$ , производная $\left(x\right)'=1$ производная числа $\left(2\right)'=0$, константа.
- производная линейного с коэффициентом: правило выноса числа за знак производной $\left(-3x\right)'=-3\cdot\left(x\right)'=-3\cdot1$
- Отображения: $f\left(x\right)$ :: $x$ $\to$ $x^3-3x+2$ $f'\left(x\right)$ :: $x$ $\to$ $3x^2-3$
1-ий главный вопрос: Что под производным? Штрих чего? Что дифференцируется? (?)'
- Варианты ответов на (?)': ... сумма нескольких ... умножение 2-х .... деление, дробь ... функция ...
- Первые трое ситуации разрешаются по правилам дифференцирования ... изучив по частьям ...
- В случае с (функция)' важно разобраться (какая функция ?)' и действовать по таблице производных
- Варианты стандартных, элементарных функций: квадрат, куб, степень, корень, тригонометрические sin, cos, tg, ctg, показательные $e^x$, $2^x$, логарифмические ln, log, lg.
Задача 2: Найти производную функции $f\left(x\right)=\left(x+2\right)^2\left(x-1\right)+1$
- $\left(f\left(x\right)\right)'=\left(\left(x+2\right)^2\left(x-1\right)+1\right)'$ - решение:
- $\left(\left(x+2\right)^2\left(x-1\right)+1\right)'=\left(\left(x+2\right)^2\right)'\left(x-1\right)+\left(\left(x+2\right)^2\right)\left(x-1\right)'+1'=2\left(x+2\right)\left(x-1\right)+\left(x+2\right)^2=3x\left(x+2\right)$
Комментарии: 1. На первом шаге: производная суммы по правилу сложения производных от каждого слагаемого. От 1 производная 0. 2. На втором шаге: производная умножения по правилу ... производные 1-го на просто 2-ое + наоборот. 3. На третьем шаге: производная квадрата равна дважды то, что под квадратом. 4. В результате: $f'\left(x\right)=2\left(x+2\right)\left(x-1\right)+\left(x+2\right)^2$ - производная функции. 5. Отображения: $f\left(x\right)$ :: $x$ $\to$ $\left(x+2\right)^2\left(x-1\right)+1$ $f'\left(x\right)$ :: $x$ $\to$ $2\left(x+2\right)\left(x-1\right)+\left(x+2\right)^2$ 6. .
Задача 3: Найти производные от заданных функций:
$\left(-\frac{5x^6}{7}\right)'=-\frac{5}{7}\cdot \left(x^6\right)'=-\frac{5}{7}\cdot 6\cdot x^5=-\frac{30}{7}\cdot x^5$
$\left(\frac{4}{7\sqrt{x}}-9\right)'=\frac{4}{7}\cdot \left(\frac{1}{\sqrt{x}}\right)'-\left(9\right)'=\frac{4}{7}\cdot \left(x^{-\frac{1}{2}}\right)'-0=\frac{4}{7}\cdot \left(-\frac{1}{2}\right)\cdot x^{-\frac{1}{2}-1}=-\frac{2}{7x\sqrt{x}}$
$\left(2x^4-5x^2+7x-13\right)'=\left(2x^4\right)'-\left(5x^2\right)'+\left(7x\right)'-\left(13\right)'=2\cdot 4x^3-5\cdot 2x+7\cdot x^0=8x^3-10x+7$
$\left(\left(5-x^2\right)\cdot \left(\sqrt{x}+7\right)\right)'=\left(5-x^2\right)'\cdot \left(\sqrt{x}+7\right)+\left(5-x^2\right)\cdot \left(\sqrt{x}+7\right)'=-2x\cdot \left(\sqrt{x}+7\right)+\frac{5-x^2}{2\sqrt{x}}$
$\left(\frac{1-3x}{x^2-3x+2}\right)'=\frac{\left(1-3x\right)'\cdot\left(x^2-3x+2\right)-\left(1-3x\right)\cdot\left(x^2-3x+2\right)'}{\left(x^2-3x+2\right)^2}=\frac{-3\cdot\left(x^2-3x+2\right)-\left(1-3x\right)\cdot\left(2x-3\right)}{\left(x^2-3x+2\right)^2}=\frac{3\cdot x^2-2x-3}{\left(x^2-3x+2\right)^2}$
Комментарии: 1. Что под (?)' : умножение отрицательно дробного числа на степень. Здесь числа 5 и 7 всего лишь числовые множитель-делитель. Не надо знаменатель число 7 воспринимать как участник правила деления с возведением в квадрат. Простой множитель $-\frac{5}{7}$ выносится за знак штрихования как множитель. 2. Здесь под (?)' вычитание, а значит правило суммы и далее формула степени (- дробной). 3. под (?)' четыре слагаемых ... по правлу суммы аккуратно штрихуем каждое. 4. под (?)' находится умножение двух ... по правилу произведения конструируем плюсовую коммутацию производных ... отдельно дифференцируем каждый множитель. 5. Тут дробь, деление под (?)' ... знаменатель в квадрат, в числителе коммутация с минусом. .
Задача 4: Примеры вычисления производных в картинках:
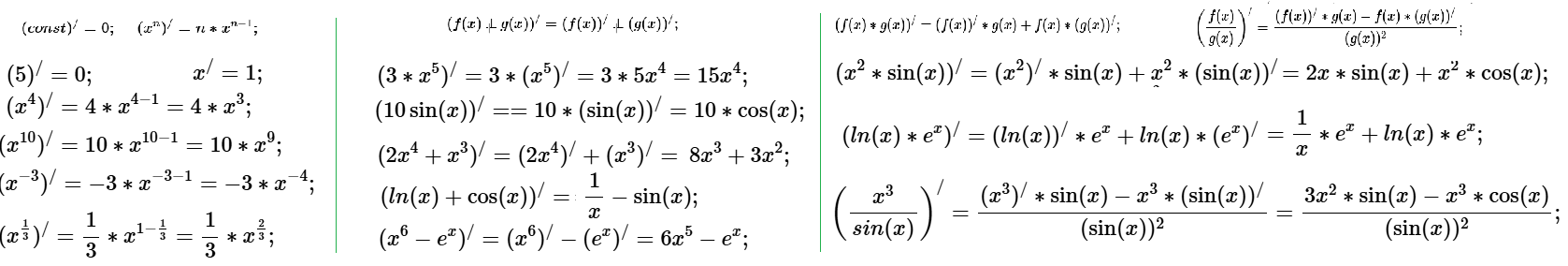


Аргумент функции ax + b - сложная функция
2-ой главный вопрос: Что под функцией? каков аргумент? f'(?) . Просто х или что-то сложное?
Задача 5: Найти производную сложной функций $\left(\left(3x-1\right)^2\right)'$
- Сложная функция: внутренняя $g\left(x\right)=3x-1$ и внешняя $f\left(g\right)=\left(g\left(x\right)\right)^2$ - квадрат от аргумента, от внутренней
- Метод Замены: Введем новую переменную $X=3x-1$ ... "внутренняя функция стала переменной от $x$ "
- $\left(\left(3x-1\right)^2\right)'=\left(X^2\right)'\cdot X'=2X\cdot X'=2\left(3x-1\right)\cdot \left(3x-1\right)'=2\left(3x-1\right)\cdot 3=18x-6$. Или, короче:
- $\left(\left(3x-1\right)^2\right)'=2\left(3x-1\right)\cdot \left(3x-1\right)'=2\left(3x-1\right)\cdot 3=18x-6$ (замена $X=3x-1$ в воображении)
- Хорошие вопросы: Производная Чего? в этом случае "квадрата". Что есть внешняя и что есть внутренняя функции?
Теорема: Производная Сложной Функции по аргументу $x$ равна умножению
производной внешней функции по внутренней на производной внутренней функции по $x$.
$\left(f\left(g\left(x\right)\right)\right)'=f_g'\cdot g_x'$ Метод Замены: $\left(f\left(g\left(x\right)\right)\right)'=\left(f\left(X\right)\right)'=f_X'\left(X\right)\cdot X'$.
$X=g\left(x\right)$ - внутреннее выражение. Доказательство через осмысление предела: $\frac{\bigtriangleup f\left(g\left(x\right)\right)}{\bigtriangleup x}=\frac{\bigtriangleup f\left(g\right)}{\bigtriangleup g}\cdot \frac{\bigtriangleup g\left(x\right)}{\bigtriangleup x}$
Таблица производных для линейного аргумента $ax+b$ - линейная функция от $x$
-
Степень: $\left((ax+b)^n\right)'=n\cdot (ax+b)^{n-1}\cdot a$ $\left((ax+b)^3\right)'=3\cdot (ax+b)^2\cdot a$
-
Корень: $\left(\sqrt{ax+b}\right)'=\left((ax+b)^{\frac{1}{2}}\right)'=\frac{1}{2}\cdot (ax+b)^{-\frac{1}{2}}\cdot a$ $\left(\sqrt[3]{ax+b}\right)'=\left((ax+b)^{\frac{1}{3}}\right)'=\frac{1}{3}\cdot (ax+b)^{-\frac{2}{3}}\cdot a$
-
Тригонометрические: $\left(\sin (ax+b)\right)'=a\cdot \cos (ax+b)$ $\left(\cos (ax+b)\right)'=-a\cdot \sin (ax+b)$
-
Экспоненциальные: $\left(e^{ax+b}\right)'=a\cdot e^{ax+b}$ $\left(a^{ax+b}\right)'=a\cdot a^{ax+b}\cdot \ln a$
-
Логарифмические: $\left(\ln (ax+b)\right)'=a\cdot \frac{1}{ax+b}$ $\left(\log _a(ax+b)\right)'=\left(\frac{\ln (ax+b)}{\ln a}\right)'=a\cdot \frac{1}{(ax+b)\cdot \ln a}$
Задача 6: Найти производные "сложных" функций
A. $\left(\sin7x\right)'=7\cos7x$
B. $\left(\sqrt{5x-6}\right)'=\frac{1}{2\sqrt{5x-6}} \cdot 5=\frac{5}{\sqrt{5x-6}}$
C. $\left(e^{-4x}\right)'=e^{-4x}\cdot (-4)=-4e^{-4x}$
D. $\left(\cos (3x+2)\right)'=\sin (3x+2) \cdot (-3)=-3\cdot\sin (3x+2)$
E. $\left(\log_3\left(5-2x\right)\right)'=\left(\frac{\ln (5-2x)}{\ln3}\right)'=\frac{1}{\ln3\cdot (5-2x)}\cdot (-2)=-\frac{2}{\ln3\cdot\left(5-2x\right)}$
Комментарии: A. каков аргумент? f'(?): здесь по синусом 7х, то есть линейная функция 7х+0. Значит, производную по таблице надо умножать на коэффициент 7, стоящий перед переменной х. B. В аргументе корня, под радикалом линейная 5х-6, ... , производную по у = 5х-6 домножаем на коэффициент 5. C. Если б было просто $e^x$, мы бы штриховали по таблице, но здесь аргумент экспоненты -4х+0 ... значит, табличный результат умножаем на -4 D. Под косинусом линейная 2х+3, воспринимаем его как у = 2х+3 ... штрихуем по у .... возвращаем вместо у истинное 2х+3 ... результат умножаем на коэффициент 2. E. В аргументе логарифма 5-2х: приминяем формулу дифференцирования логарифма к сложному аргументу и итог домножаем на -2 ... так, как -2 коэффициент линейной 5-2х. .
$\left(\cos (3x+2)\right)'=$ .... $3x+2 \to y$ $\left(\cos y\right)'=-\sin (y)$ $y \to 3x+2 $ .... $\left(\cos (3x+2)\right)'=\sin (3x+2) \cdot (-3)=-3\cdot\sin (3x+2)$
Дифференцирование сложных функций, ... ... "как замена" и умножение на производную "замены":
- Производная сложной функции ... в аргументе функции выражение от $x$, называем "заменой" $X$ :
- $\left(f\left(X\right)\right)'=f'\left(X\right)\cdot\left(X\right)'$. В сложных функциях надо распознать и выделить внешнюю и внутреннюю функцию.
- Найти производную внешней функции и умножить на производную внутренней функции.
- f- внешняя функция, $X$ - внутренняя. $f'\left(X\right)$ - производная в $X$ !
Еще раз: Главный вопрос при дифференцировании:
- Что находится под производным? $\left(....\right)'$ Штрих чего мы ищем?
- Варианты: умножение, деление, сумма, умножение на число, функция.
- Если функция, то какая? квадрат, степень, тригонометрия, экспоненциальная, логарифм, корень?
- Если квадрат, то чей? Если логарифм, то от чего? Если тригонометрия, то от какого аргумента?
- В сложных функциях важно правильно распознать внешнюю и внутреннюю функцию. И, перемножить их производные.
Задача 7: Найти производную $\left(\sqrt{3x}\cos\left(4x+1\right)\right)'$
-
перед нами произведение двух функций , возьмем производную от умножения по формуле
-
$\left(fg\right)'=f'g+fg'$ : $\left(\sqrt{3x}\right)'\cos\left(4x+1\right)+\sqrt{3x}\left(\cos\left(4x+1\right)\right)'$ .
-
функции , от которых предстоит взять производную, являются сложными .... производные сложных?
-
важно правильно распознать, какая функция будет внешней, а какая внутренней для каждой сложной функции.
-
$\sqrt{3x}$ : внешняя функция - квадратный корень ; внутренняя - выражение под корнем $3x$ , берем производную:
-
$\left(\sqrt{3x}\right)'=\frac{1}{2}\left(3x\right)^{\frac{1}{2}-1}\cdot\left(3x\right)'=\frac{1}{2}\left(3x\right)^{-\frac{1}{2}}\cdot3=\frac{3}{2\sqrt{3x}}$
-
$\cos\left(4x+1\right)$ : внешняя функция - тригонометрическая cos ; внутренняя - аргумент косинуса $4x+1$
-
$\left(\cos\left(4x+1\right)\right)'=-\sin\left(4x+1\right)\cdot\left(4x+1\right)'=-\sin\left(4x+1\right)\cdot4x'=-4\sin\left(4x+1\right)$
-
Cоберем все наши выкладки и получим производную исходного выражения:
-
$\left(\sqrt{3x}\right)'\cos\left(4x+1\right)+\sqrt{3x}\left(\cos\left(4x+1\right)\right)'=\frac{3}{2\sqrt{3x}}\cos\left(4x+1\right)-4\sqrt{3x}\sin\left(4x+1\right)$
Таблица, напоминание о производной:
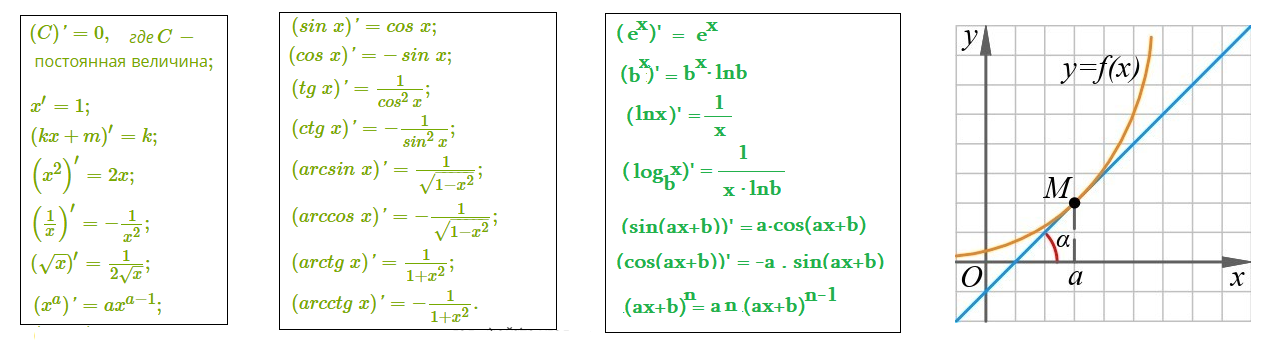
Упражнения (A):
Упражнения (В):
Упражнения (С):
Интерактивная Доска: