Напоминание: производное в точке, касательная к графику в точке. Наклон.
Приближенным значением производной функции в точке $x_{0}$ со сдвигом 0,01 называется значение
$f'\left(x_0\right)\approx \frac{f\left(x_0+0,01\right)-f\left(x_0\right)}{\left(x_0+0,01\right)-\left(x_0\right)}$ $f'\left(a\right)\approx \frac{f\left(a+h\right)-f\left(a\right)}{\left(a+h\right)-\left(a\right)}$ Точное: $f'\left(a\right)=\lim \frac{f\left(a+h\right)-f\left(a\right)}{\left(a+h\right)-\left(a\right)}$ при $\lim h=0$
- Производная в точке - это отношение: (приращение самой функции) / (малое приращение аргумента в этой точке).
- Физический смысл - производная функции показывает скорость изменения функции: роста или убывания функции.
- Геометрический смысл - производная в каждой точке равна тангенсу угла наклона касательной, проведенной к ее графику.
Задача 1: Дана функция $f\left(x\right)=x^3-3x+2$ . Вычислить приближенное производную $f'\left(x_0\right)$
- в точке $x_0=1,2$ со сдвигом $h=0,2$ ? $\Rightarrow$ $f'\left(1,2\right)\approx \frac{\bigtriangleup f\left(x\right)}{\bigtriangleup x}\approx \frac{f\left(1,2+0,2\right)-f\left(1,2\right)}{1,4-1,2}=\frac{1,4^3-3\cdot 1,4+2-\left(1,2^3-3\cdot 1,2+2\right)}{0,2}=1,555$
- в точке $x_0=0,4$ со сдвигом $h=0,0001$ ? $\Rightarrow$ $f'\left(0,4\right)\approx \frac{f\left(0,4+h\right)-f\left(0,4\right)}{\left(0,4+h\right)-0,4}=\frac{\left(0,4+h\right)^3-3\cdot \left(0,4+h\right)+2-\left(0,4^3-3\cdot 0,4+2\right)}{h}=$
- $=\frac{\left(0,4+h\right)^3-0,4^3}{h}-\frac{3\cdot \left(0,4+h\right)-3\cdot 0,4}{h}=\frac{0,4^3+3\cdot 0,4^2\cdot h+3\cdot 0,4h^2+h^3-0,4^3}{h}-3=\left(3\cdot 0,4^2-3\right)+h\cdot \left(3\cdot 0,4+h\right)\approx 2,5201$
- точное производное $f'\left(0,4\right)=3\cdot 0,4^2-3=2,52$ при $h\sim 0$ !
- Наклон касательной - тангенс угла $k=\frac{f\left(x+0,000001\right)-f\left(x\right)}{x+0,000001-x}$ . Точнее, "примерно равен". Точнее: при малом h!.
- ....еще точнее "в пределе равен". lim $\frac{f\left(a+h\right)-f\left(a\right)}{h}$. Точка (a+h; f(a+h)) сближается с точкой (a; f(a)) при малом h !.
- Производная f'(a) равен тангенсу угла наклона c x-осью касательной к графику функции f в точке (a, f(a)).
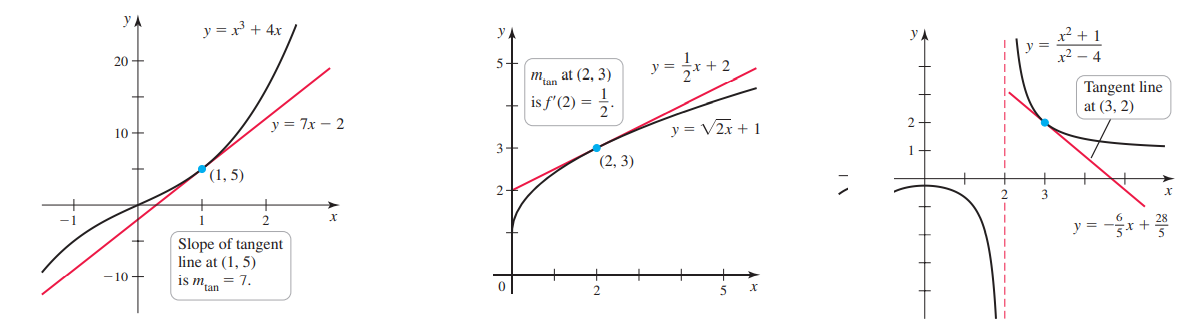
Уравнение касательной к графику функции $y=f\left(x\right)$ в точке $x=x_0$ : $y=f\left(x_0\right)+f'\left(x_0\right)\cdot\left(x-x_0\right)$ - касательная, прямая
- Функция $y=f\left(x\right)$ и её касательная $y=kx+b$ в точке касания $x=x_0$ имеют одинаковые значения, наклон, производные.
- Наклон касательной = производное функции $k=f'\left(x_0\right)$ определяет как "течет" график: растет, убывает?
- Наклон положительный, $k>0$ - касательная справа-налево - производная $>0$ - функция растет - график функции "течет" вверх.
- Наклон отрицательный, $k<0$ - касательная слево-направо - производная < 0 - функция убывает - график функции "течет" вниз, по склону.
Производная - как детектор поведения функции
Вопрос: Как влияет на поведение функции $f\left(x_0\right)$ около точки $x=x_0$ значение производной $f'\left(x_0\right)$ ?
- Из определения производной в точке $x=x_0$ $\Rightarrow$ $f'\left(x_0\right)\approx\frac{f\left(x_0+0,01\right)-f\left(x_0\right)}{x_0+0,01-x_0}$
- выразим значение функции чуть правее точки $x_0$ : $f\left(x_0+0,01\right)\approx f\left(x_0\right)+0,01f'\left(x_0\right)$. Значит, функция будет иметь большее значение правее от $x_0$ , если только $f'\left(x_0\right) > 0$.
- Аналогичные рассуждения для значения функции чуть левее. Из $f'\left(x_0\right)\approx\frac{f\left(x_0-0,01\right)-f\left(x_0\right)}{x_0-0,01-x_0}$ $\Rightarrow$ $f\left(x_0-0,01\right)\approx f\left(x_0\right)-0,01\cdot f'\left(x_0\right)$ $\Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
- Сформулируем ответы на вопрос о влиянии знака производной в данной точке:
- если $f'\left(x_0\right) > 0$ то $f\left(x_0-0,01\right) < f\left(x_0\right) < f\left(x_0+0,01\right)$ $\Rightarrow $ функция растет (см. слева направо).
- если $f'\left(x_0\right) < 0$ то $f\left(x_0-0,01\right) > f\left(x_0\right) > f\left(x_0+0,01\right)$ $\Rightarrow $ функция убывает, график идет вниз.
- если $f'\left(x_0\right)=0$ то ситуации более запутанные: при $f\left(x_0-0,01\right) < f\left(x_0\right) > f\left(x_0+0,01\right)$ точка $x=x_0$ называется точкой максимума. В нем функция "выше", чем по-соседству хоть слева, хоть справа.
В случае $f\left(x_0-0,01\right) > f\left(x_0\right) < f\left(x_0+0,01\right)$, $x=x_0$ - точка минимума. Если ни то, ни другое, то точка перегиба.
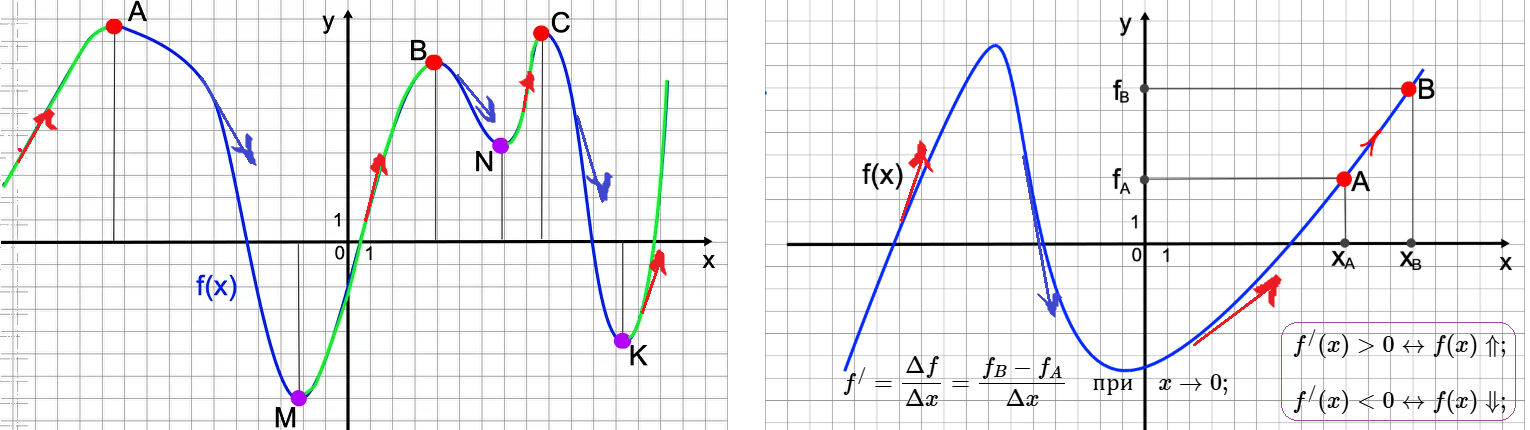
Взаимное влияние графика функции и графика ее производной функции
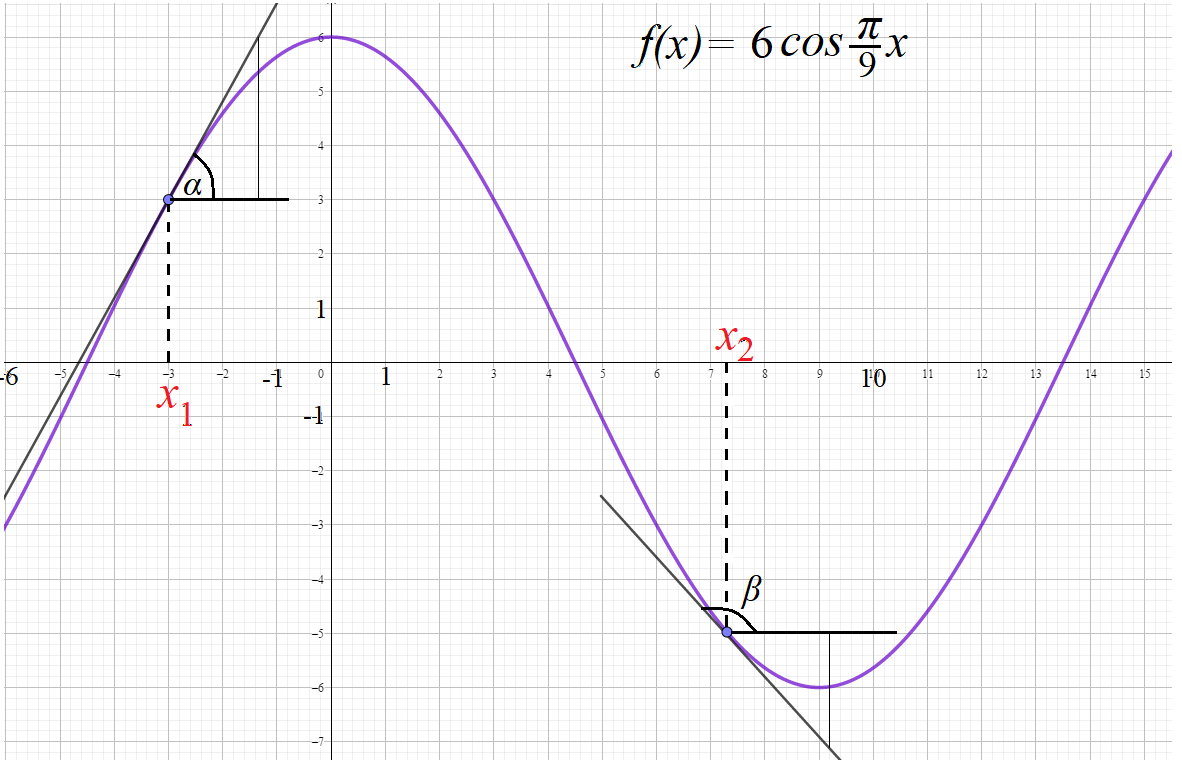
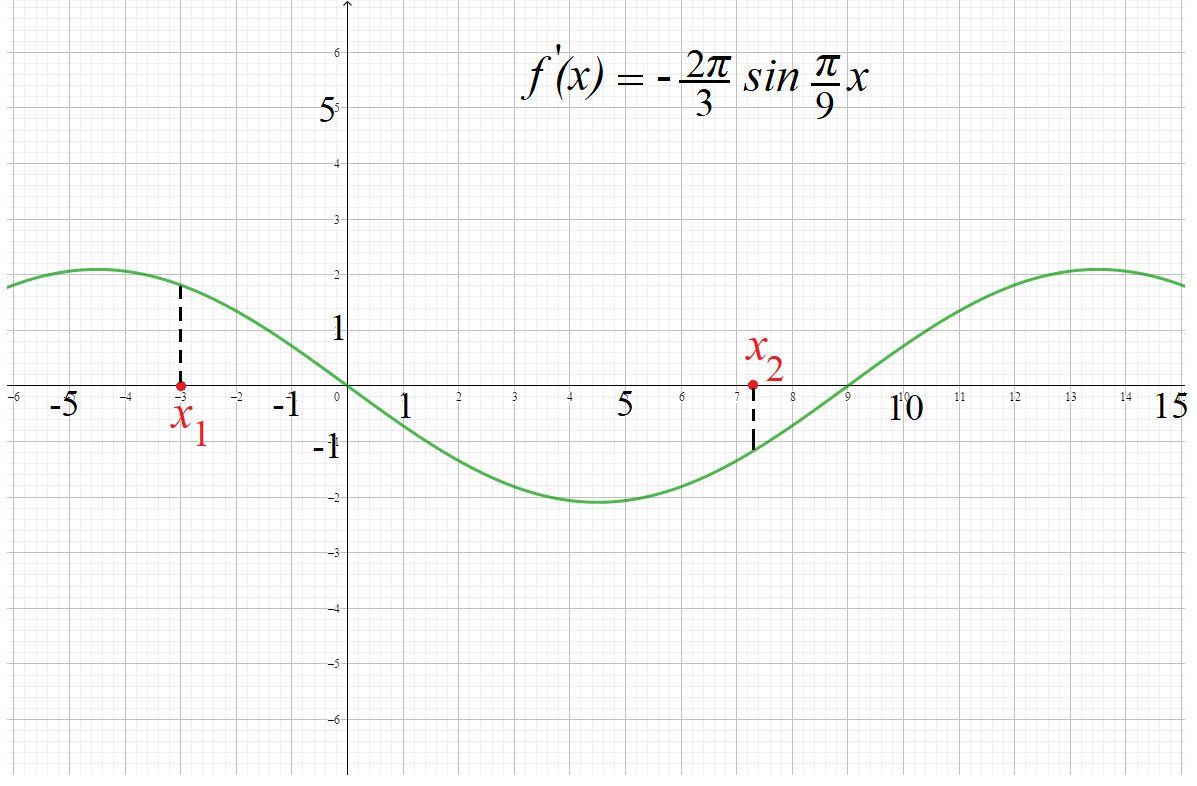
Задача 2: Каково взаимовлияние графика $f\left(x\right)=6\cos\frac{\pi}{9}x$ и графика ее производной $f'\left(x\right)=-\frac{2\pi}{3}\sin\frac{\pi}{9}x$
- Производная от какой-то функции - это некая, связанная с ней функция, характеризующая поведение самой функции
- Рассмотрим точку $x_1=-3$ . В нем сама функция равна $f\left(-3\right)=6\cos\frac{\pi}{9}(-3)=3$ , а ее производная - $f'\left(-3\right)=-\frac{2\pi}{3}\sin\frac{\pi}{9}(-3)\approx1,77$,
- График график проходит в точке $(-3;3)$. Каково поведение графика около этой точки? Растет или убывает?
- Насколько быстро растет или убывает? На все эти вопросы ответы дает производная. Производная в точке $(-3;3)$, $x_1=-3$ положительна, поэтому растет!
- Около точки $x_1=-3$ функция приближенно $f\left(x\right)\approx 3+1,77\cdot(x+7)$
- Т.к. производная равна $1$, то тангенс угла наклона касательной, проведенной к графику нашей функции в данной точке ($-3; 3$) равен $1$.
- Значит, касательная направлена под углом $45$ градусов, ведь $\tg45=1$.
- Значит, функция около этой точки растет "умеренно", примерно под углом 45 градусов.
Значение производной $f'\left(x_0\right)$ в какой-либо точке указывает на рост или убывание исходной функции $f\left(x\right)$ около этой точки $x_0$. Зная числовое значение производной, можно определить как ведет себя функция: стоит ли на месте, растет или убывает и как быстро изменяется. Производная от функции помогает узнать в каждой точке характер скорости изменений, поведения графика самой функции.
-
В тех точках, где функция растет - график поднимается вверх (если смотреть слева направо) - касательная к графику в этой точке наклонена вправо - - тангенс наклона положительный - производная в этой точке имеет положительное значение.
-
В тех точках, где функция убывает - график опускается вниз (если смотреть слева направо) - касательная к графику в этой точке наклонена влево - - тангенс наклона отрицательный, тупой угол - производная в этой точке имеет отрицательное значение.
-
Производная = 0 функция "остановилась", "касательная горизонтальна", точка экстремума: минимум, максимум или перегиб.
-
Вторая производная в точке x показывает скорость изменения скорости, т.е. ускорение в этой точке. Вторая производная = 0 означает "ускорение обнулилось". больше нуля - выпукло вниз (min), меньше нуля - вверх (max).
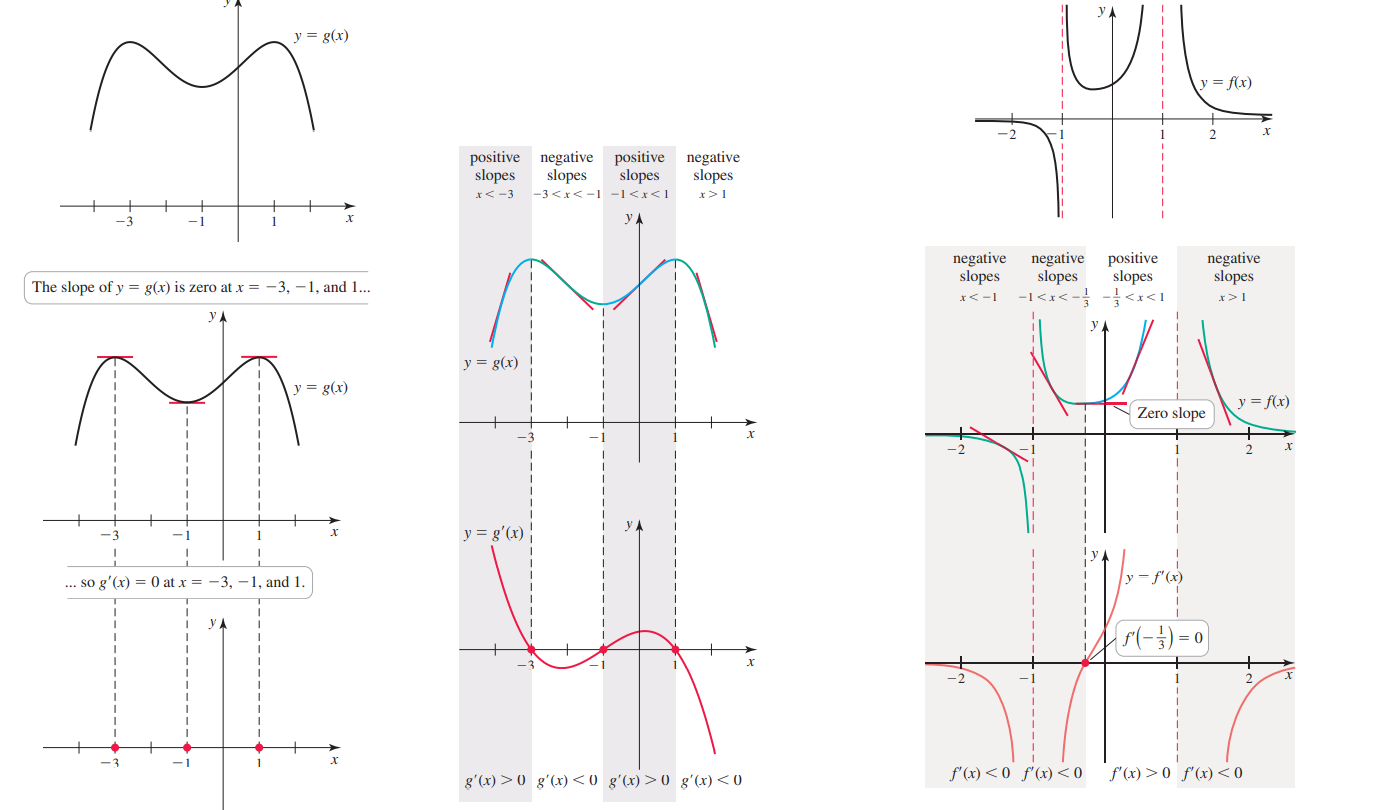
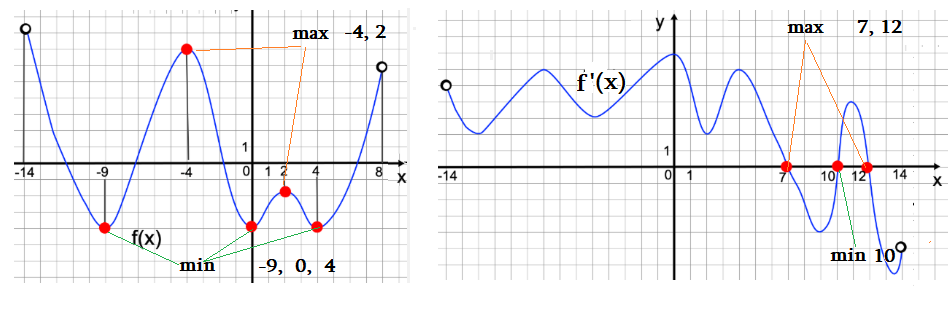
Задача 3: На рисунке изображён график функции y = f(x) и на оси абсцисс отмечены точки: x1, x2, x3, x4, x5, x6, x7, x8. В каких из этих точек производная функции y = f(x) отрицательна?
- Функция убывает там, где производная от функции отрицательна; Убывает ... наклон отрицательный ... касательная вправо-вниз.
- Около точки $x_6$ видно, что: график убывающий, наклон вправо-вниз, $\Rightarrow$ $f'(x_6)<0$. То что надо!
- Смотрим все точки (убывает-возрастает? касательная вниз-вверх?). Выбираем 4 с $f'(x)<0$: $x_2$, $x_4$, $x_6$, $x_8$.
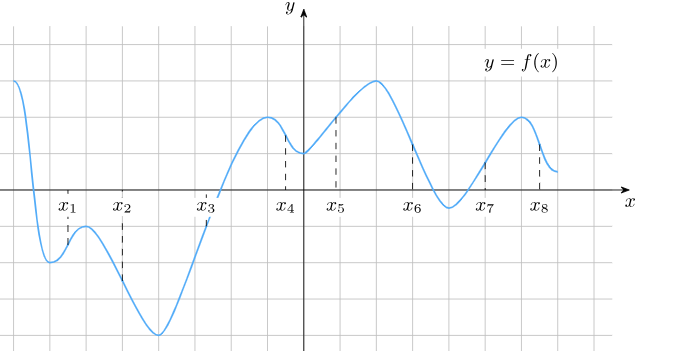
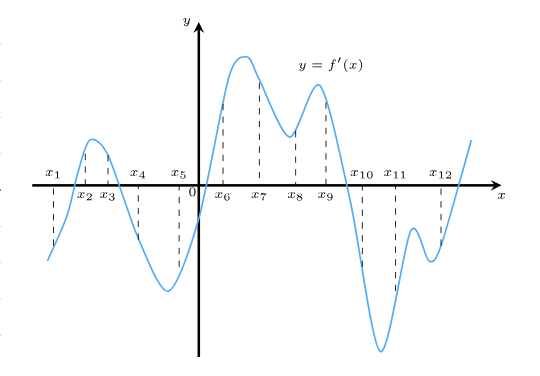
Задача 4: На рисунке изображён график функции y = f′(x) — производной функции f(x). На оси абсцисс отмечены точки: x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12. Какие из них принадлежат промежуткам возрастания функции
- Функция возрастающая тех точках, в которых производная положительна; Т.е. точка графика $f'(x)$ должен быть в верхней части.
- В точке $x_7$ график находится в верхней полуплоскости, y-координата положительная. Значит, $f'(x_7)>0$ $f(x_7)$ ⇑
- Ищем те точки, в которых $f'(x)>0$ $\Rightarrow$ $f(x_7)$ ⇑ : 6 точек роста: $x_2$, $x_3$, $x_6$, $x_7$, $x_8$, $x_9$,
⇑ ⇑ ⇑ ⇑ ⇓ ⇓ ⇓ ⇓
Задан График функции, y = f(x):
- f(x) > 0 :. Функция положительна в тех х - промежутках, где график находится в верхней полуплоскости, y > 0.
- f(x) < 0 :. Функция отрицательна в тех х - промежутках, где график находится в нижней полуплоскости, y < 0
- f(x) = 0 :. Функция обнуляется в тех х - числах, где график пересекается с абсцисой, y = 0. Корни функции f(x).
- f(x) ⇑ :. Функция растет в тех х - точках, около которых график поднимается вправо-вверх. Касательная ⇑.
- f(x) ⇓ :. Функция убывает в тех х - точках, около которых график опускается вправо-вниз. Касательная ⇓.
- f(x) ⇑ :. Функция возрастает ⇒ производная от функции положительна; f'(x) > 0.
- f(x) ⇓ :. Функция убывает ⇒ производная от функции отрицательна; f'(x) < 0.
- f(x) min-max. Функция принимает максим или миним значение в точке ⇒ производная от функции равна нулю; f'(x) = 0.
Задан График производной функции, y = f'(x) (от некой функции y = f(x) ) :
- В заданиях этого типа дан график производной, нужно сделать выводы про функцию, от которой эта производная взята.
- f'(x) > 0 :. Производная > 0 в тех х - точках, где график производной находится в верхней полуплоскости, y > 0.
- f'(x) < 0 :. Производная < 0 в тех х - точках, где график находится в нижней полуплоскости, y < 0
- f'(x) = 0 :. Производная обнуляется в тех х - числах, где график пересекается с абсцисой, y = 0. Корни производной f'(x).
- f'(x) > 0 : Производная от функции положительна ⇒ функция возрастает; f(x) ⇑.
- f'(x) < 0 : Производная от функции отрицательна ⇒ функция убывает; f(x) ⇓.
- f'(x) = 0 : Производная от функции равна нулю ⇒ функция принимает максим или миним значение в этой точке; f(x) min-max.
Аналитически: нахождение интервалов возрастания / убывания функции
- Чтоб найти на каких промежутках убывает функция: надо найти ее производную и решить неравенство $f'(x)<0$ !
Теорема: Интервалы возрастания функции $\Leftrightarrow$ решению неравенства $f'(x)>0$ .
- Функция возрастает ⇒ производная от функции положительна; $f(x)$ ⇑ $\Leftrightarrow$ $f'(x)>0$
- Функция убывает ⇒ производная от функции отрицательна; $f(x)$ ⇓ $\Leftrightarrow$ $f'(x)<0$
- Функция принимает максимальное или минимальное значение в точке ⇒ производная от функции равна нулю; $f'(x)=0$
Задача 5: Указать интервалы монотонности функции $f\left(x\right)=x^3-3x+2$ . ;
- $f\left(x\right)=x^3-3x+2$ Функция
- $\left(x^3-3x+2\right)'=3x^2-3$ находим производную $f'\left(x\right)$ от нашей функции
- $3x^2-3>0$ $\left(-\infty ;-1\right)\ \left(1;\infty \right)$ интервалы возрастания, неравенство больше, $f'\left(x\right)>0$
- $3x^2-3<0$ $\left(-1;1\right)$ интервалы убывания, производное минус, $f'\left(x\right)<0$
- $M_f$ $ \left(-\infty ;-1\right)+\left(-1;1\right)+\left(1;+\infty \right)$ области монотонности
Область знакопостоянства: где функция положительна? f(x) > 0 ? На каких интервалах отрицательна? В каких х - точках какого знака?
Область монотонности: На каких промежутках функция возрастает? f(x) > 0 ? где функция убывает? В каких х - точках производная какого знака?
Поведение функции f(x) : отрицательность $\Leftrightarrow$ f(x) < 0 возрастание $\Leftrightarrow$ f'(x) > 0 убывание $\Leftrightarrow$ f'(x) > 0
Задача 6: Дана функция $f\left(x\right)=\frac{1}{3}x^3-4x+3$ Найти промежутки знакопостоянства (положительности, отрицательности) и монотонности (возрастания, убывания)
- Решение, (1): Напишем и решим неравенства функция > 0 и функция < 0. Найдем критические точки функция = 0
- $\frac{1}{4}x^3-6x-10=0$ (f(x) = 0, кубическое? Угадаем корень $x=-2$, разложим на множители)
- $x^3-24x-40=0$ $\Leftrightarrow$ $x^3+2x^2-2x^2-4x-20x-40=0$
- $x^2\left(x+2\right)-2x\left(x+2\right)-20\left(x+2\right)=0$ $\Leftrightarrow$ $\left(x+2\right)\left(x^2-2x-20\right)=0$
- $x^2-2x-20=0$ $\Leftrightarrow$ $x=1-\sqrt{21}$ $x=1+\sqrt{21}$
- $\frac{1}{4}x^3-6x-10=0$ $\Leftrightarrow$ $x=-2$ $x=1-\sqrt{21}$ $x=1+\sqrt{21}$ (корни кубического)
- $1-\sqrt{21}<-2<1+\sqrt{21}$ (критические точки, интервалы)
- $\frac{1}{4}x^3-6x-10>0$ $(1-\sqrt{21};-2)$ $x>1+\sqrt{21}$ функция > 0
- $\frac{1}{4}x^3-6x-10<0$ $x<1-\sqrt{21}$ $-2<x<1+\sqrt{21}$ функция < 0
- Решение, (2): Найдем производное f'(x) и решим неравенства: производное > 0 и производное < 0. Монотонность!
- $\left(\frac{1}{4}x^3-6x-10\right)'=\frac{3}{4}x^2-6$
- $\frac{3}{4}x^2-6=0$ $3x^2-6\cdot 4=0$ $x^2-8=0$ $x=-2\sqrt{2}$ $x=2\sqrt{2}$
- $\frac{3}{4}x^2-6>0$ $x<-2\sqrt{2}$ $x>2\sqrt{2}$ производное > 0
- $\frac{3}{4}x^2-6<0$ $-2\sqrt{2}<x<2\sqrt{2}$ производное < 0
- $M_f$ интервалы монотонности $ \left(-\infty ;-2\sqrt{2}\right)+\left(-2\sqrt{2};2\sqrt{2}\right)+\left(2\sqrt{2};+\infty \right)$
Уточнение терминов: интервал, промежуток, возрастающая, не убывающая, неотрицательная .....
- Интервал ... $(a;b)$, $(-2;3)$ .... все числа от -2 до +3, исклучая концы. Круглые (скобки).
- Промежуток ... $[a;b]$, $[-2;3])$ .... все числа от -2 до +3, в том числе концы. Квадратные [скобки].
- Функция $x^3-24x-40=0$ убывает на интервале $\left(-2\sqrt{2};2\sqrt{2}\right)$.
- $x^3-24x-40=0$ невозрастающая на промежутке $[-2\sqrt{2};2\sqrt{2}]$, т.к. в концах $f'(x)=0$, значит, не растет.
- Функция возрастает в точке ... означает "около точки", "точка принадлежит интервалу возрастания", "в окрестности точки".
- Функция в точке ... имеется в виду точка на $х$ - абсциссе, аргумент функции. например $x=-3$
- Точка графика функции - точка в системе координат, находящийся на графике. Например: $(2;-5)$ $\Rightarrow$ $f(2)=-5$
- Точка максимума - точка на $х$ - абсциссе, около (в локальной окрестности) которой функция имеет пиковое значение.
Будущее: Точки экстремумов функции. min-max.
min-max: Функция принимает наибольшее или наименьшее значение в точках, где производная равна нулю.
Размышления о точках экстремумов: Из $f'\left(x_0\right)\approx\frac{f\left(x_0+0,01\right)-f\left(x_0\right)}{x_0+0,01-x_0}$ выразим значение функции чуть правее точки $x_0$ : $f\left(x_0+0,01\right)\approx f\left(x_0\right)+0,01f'\left(x_0\right)$. Значит, функция будет иметь большее значение правее от $x_0$ , если только $f'\left(x_0\right) > 0$. Аналогичные рассуждения для значения функции чуть левее. Из $f'\left(x_0\right)\approx\frac{f\left(x_0-0,01\right)-f\left(x_0\right)}{x_0-0,01-x_0}$ $\Rightarrow$ $f\left(x_0-0,01\right)\approx f\left(x_0\right)-0,01\cdot f'\left(x_0\right)$ $\Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
Определение: Точка, в которой производная обнуляется, называется экстремумом (минимум, максимум, перегиб).
В этой точке наклон графика равен нулю, т.е. касательная к графику горизонтальна.
- если $f'\left(x_0\right) > 0$ то $f\left(x_0-0,01\right) < f\left(x_0\right) < f\left(x_0+0,01\right)$ $\Rightarrow $ функция растет (см. слева направо).
- если $f'\left(x_0\right) < 0$ то $f\left(x_0-0,01\right) > f\left(x_0\right) > f\left(x_0+0,01\right)$ $\Rightarrow $ функция убывает, график идет вниз.
- если $f'\left(x_0\right)=0$ то ситуации более запутанные: при $f\left(x_0-0,01\right) < f\left(x_0\right) > f\left(x_0+0,01\right)$ точка $x=x_0$ называется точкой максимума. В нем функция "выше", чем по-соседству хоть слева, хоть справа. В случае $f\left(x_0-0,01\right) > f\left(x_0\right) < f\left(x_0+0,01\right)$, $x=x_0$ - точка минимума. Если ни то, ни другое, то точка перегиба.
- Т. максимума - функция растет, "застывает в $x_0$" , затем убывает: Производная функции > 0, в $x_0$ = 0, затем < 0.
- Т. минимума - функция убывает, "застывает в $x_0$" , затем растет. Производная < 0, в $x_0$" = 0, затем > 0.
- min: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) > f\left(x_0\right) < f\left(x_0+0,01\right)$ , $f'\left(x_0-0.01\right) < 0$ , $f'\left(x_0+0.01\right) > 0$ ; $f''\left(x_0\right) > 0$.
- max: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) < f\left(x_0\right) > f\left(x_0+0,01\right)$ , $f'\left(x_0-0.01\right) > 0$ , $f'\left(x_0+0.01\right) < 0$ ; $f''\left(x_0\right) < 0$.
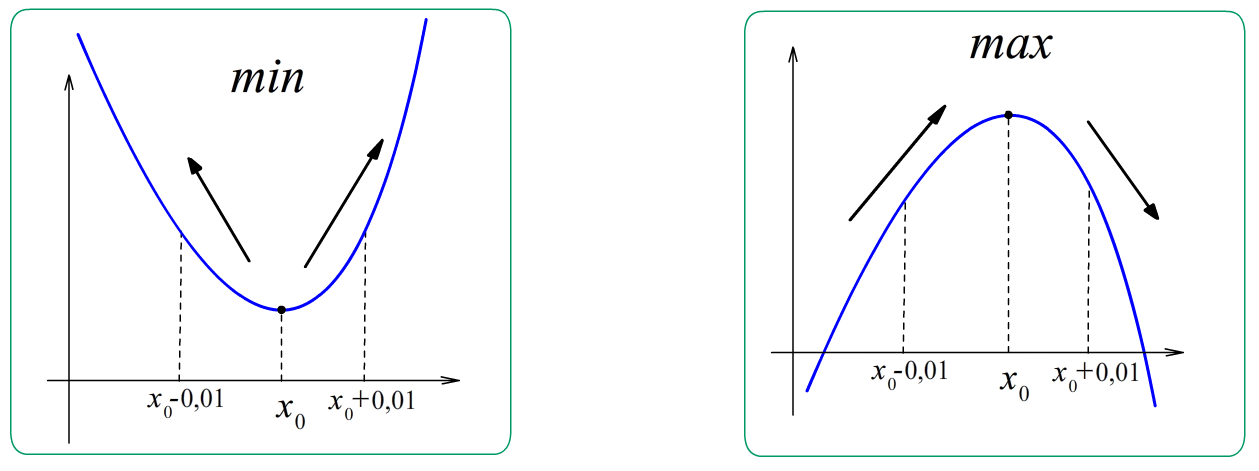
Алгоритм нахождения точек минимума (максимума) функции $y=f\left(x\right)$:
- Точка минимума - это $x$ - число, в котором производная равна нулю, а сама исходная функция от убывания переходит к возрастанию. Надо "взять" производную исходной функции и составить уравнение экстремума "производная равна нулю". Среди точек экстремума найти точку минимума. Есть три способа:
- по поведению "рост / убывание" исходной функции ;
- либо поведение "отрицательности / положительности" производной;
- либо знак второй производной в этой точке: если "производная от производной" в точке $x_0$ положительна, то это минимум.
Решаем устно:

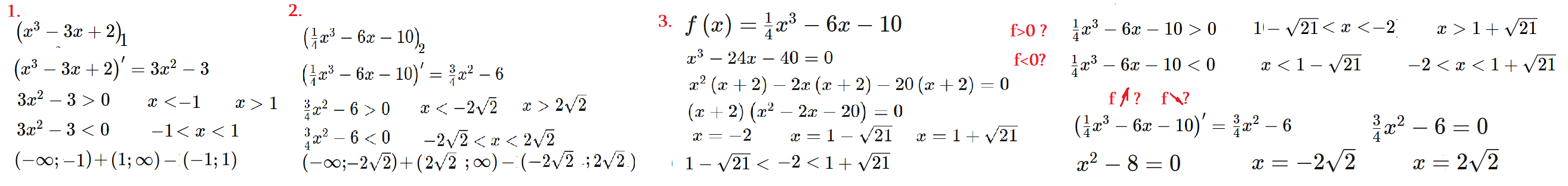
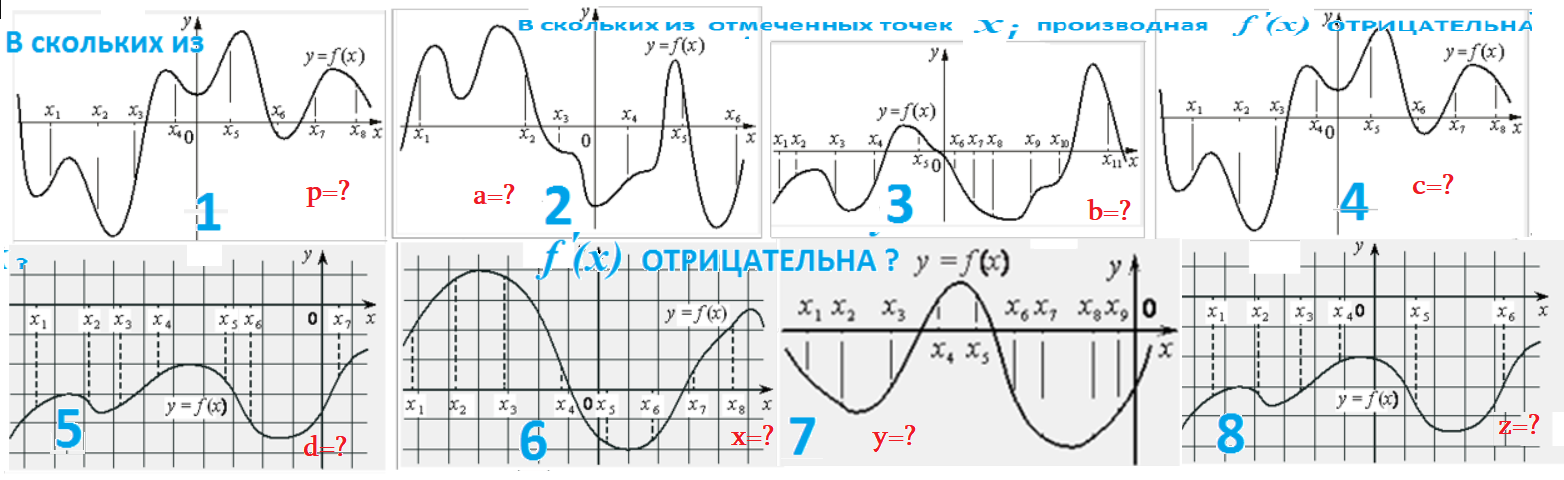

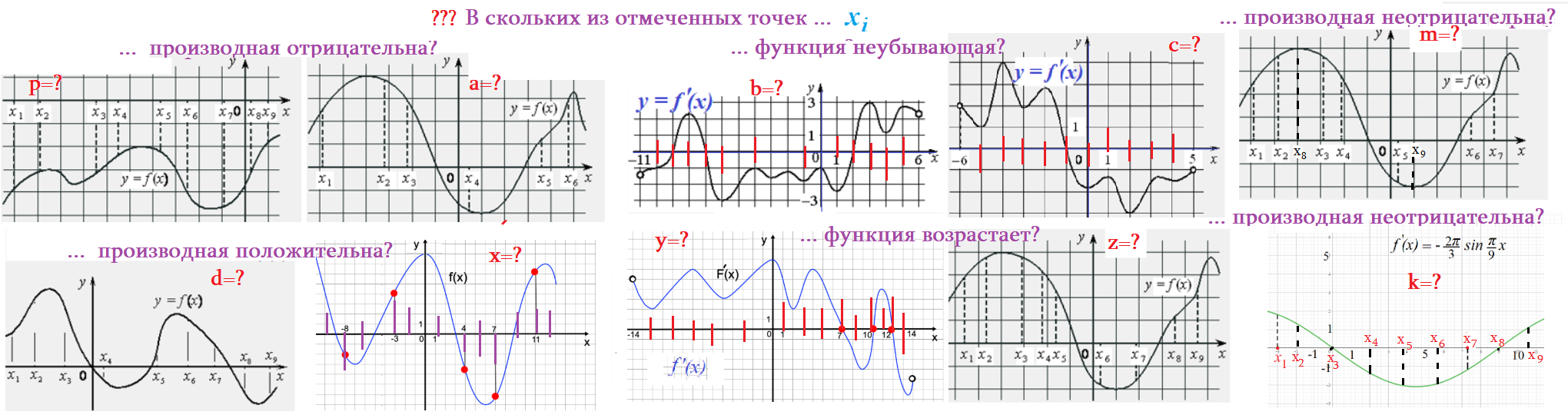

Обозначения множеств, областей
$D_f$ область определения функции, допустимые х - точки
$Z_f$ область знакопостоянства, интервалы положительности, отрицательности
$M_f$ области монотонности функции, интервалы возрастания, убывания
$X_f$ экстремумы функции, перечисление х - точек
$T_f$ уравнение касательной к функции в указанной х - точке
$E_f$ области значений функции, всевозможных у - значений
Упражнения (А):
Упражнения (В):
Упражнения (С):
