I. Вся планиметрия: теоремы, свойства, формулы на 4-х сценах

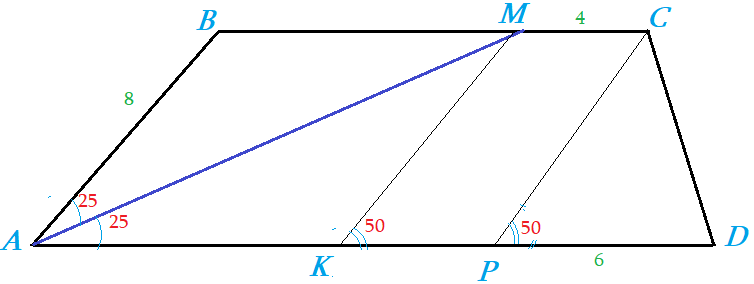
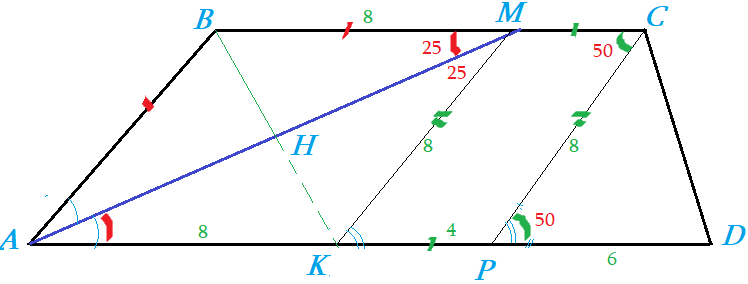
Сцена 1:    В трапеции $ABCD$   из вершины   $A$ проведена прямая   $AM$ составляющая со сторонами трапеции углы $25$ градусов. Из точки проведена $M$ прямая $MK$ к основанию под $50$ градусов. Из вершины $C$ проведенная прямая   $CP$ составляет также   $50$ градусов. Боковая сторона $AB$ равна 8, отрезок $KP$ равен 4, отрезок $PD$ равен $8$, .     Найти много чего!   

• Свойства: При пересечении двух параллельных линий с их Sекущей, образованные углы:
  
• Nакрест лежащие   углы равны                      $\angle MAD=\angle AMB$                 $\angle MCP=\angle CPD$              $\angle MKC=\angle KCP$
• Sумма Odносторонних   углов 180 град                        $\angle BAK+\angle ABC=180^o$                  $\angle KMC+\angle MCP=180^o$
• Sоответственные   углы равны                                $\angle MKP=\angle CPD$               $\angle BMK=\angle BCP$
  
•    Свойства: Uгол   =   Vершина   + два Lуча.                       .... противоположные Lучи, продолжения в обратную ... :
  
• Vертикальные   углы равны                      $\angle MAD=\angle AMB$                 $\angle MCP=\angle CPD$              $\angle MKC=\angle KCP$
• Sумма Sмежных   углов 180 град                        $\angle BAK+\angle ABC=180^o$                  $\angle KMC+\angle MCP=180^o$
•    Свойства:     Углы треугольника.    Биссектриса.      Равнобедренный треугольник:
• Bissектриса    из вершины угла делит его на два равных угла:         $\angle BAM=\angle MAK$           $\angle AKB=\angle BKM$
• Vнешний Uгол $\bigtriangleup -$ка равен сумме 2-х не Sмежных с ним.     $\angle AMC=\angle BAM+\angle ABM$               $\angle MPD=\angle PMK+\angle MKP$
• Sумма всех Uглов    треугольника равна 180 градусов.                  $\angle ABM+\angle BMA +\angle MAB=180^o$
• В Rавнобедренном Tреугольнике углы при Oсновании равны. Боковые Sтороны равны           $\angle BMA=\angle AMB$           $BA=MB$
• Sимметрии:     Ось Zеркальной sимметрии: слева и справа от Mедианы     $BH=h$   все одинаково!        $\bigtriangleup BHA=\bigtriangleup BHM$
• В Rавнобедренном: к Oснованию биссектриса, медиана и высота совпадают!    $\angle ABH=\angle HBM$      $AH=HM$      $BH \perp AM$

        

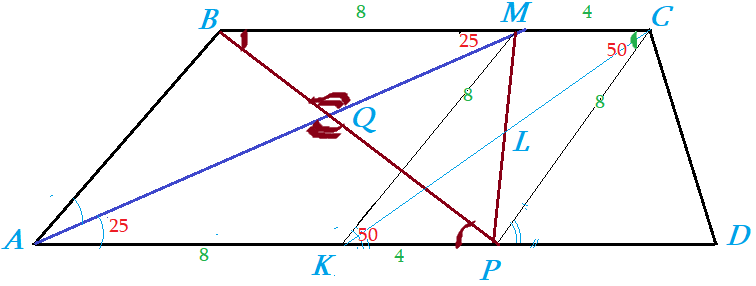
• Параллелограмм: $KMCP$      Противоположные    Sтороны   параллельны   и    равны    $KM=CP$    ,     $MC=KP$ .
• Противоположные     Uглы     $\angle KMC=\angle CPK$ ,        Сумма прилежащих Uглов $180^o$ :    $\angle KMC+\angle MKP=180$     ,     .
• Dиагонали образуют   равные   треугольники:       $\bigtriangleup MLC=\bigtriangleup KLP$      ;      $\bigtriangleup KLM=\bigtriangleup PLC$.
• Dиагонали параллелограмма делятся точкой пересечения пополам    $ML=LP=\frac{MP}{2}$      ,       $KL=LC=\frac{KC}{2}$ .
• Rомб: $ABMK$ Sимметричен относительно точки $H$ - пересечения диагоналей.      $H$ - центр Sимметрии.
• Симметричен относительно Dиагоналей.       Dиагональ - ось симметрии. .     Sтороны   равны     $AB=BM=MK=KA=a$
• Противолежащие Uглы    равны . Прилежащие в сумме 180.   Dиагонали делятся пополам .
• Dиагонали   взаимно перпендикулярны $AM \perp BK$   и   образуют равные Прямоугольные   $\bigtriangleup ABH = \bigtriangleup BHM$.
• Dиагонали    являются    Biссектрисами углов $\angle BAM=\angle MAK$ .   образуют Rавнобедренные   $\bigtriangleup$
• Tрапеция: $ABMP$ Параллельные   стороны   называются   Oснованиями,     $BM \parallel AP$ .   Другие две - боковыми сторонами.
• Сумма Oдносторонных Uглов при боковой стороне    $180^{\circ}$ :   $\angle BMP + \angle MPA = 180^{\circ}$    ,       $\angle ABM + \angle BAP = 180^{\circ}$.
• Dиагонали с основаниями   образуют равные   Nакрест лежащие углы:        $\angle MBP=\angle BPA$,         $\angle BMA=\angle MAP$
• Dиагонали с основаниями   образуют подобные треугольники           $\bigtriangleup BQM \sim \bigtriangleup AQP$            $\frac{BQM}{AQP}=(\frac{BM}{AQ})^2$

   

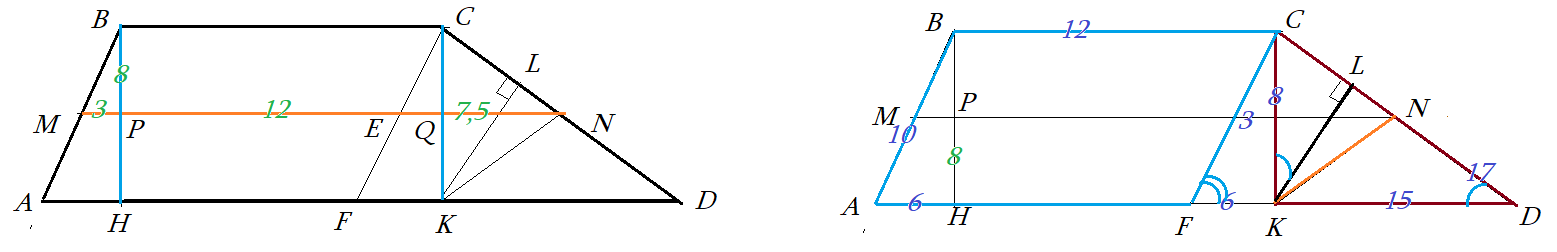
Сцена 2:    В трапеции $ABCD$   средняя линия   $MN$ разбывается высотами    $BH$ и $CK$   на три отрезка    $MP=3$,     $PQ=12$,     $QN=7,5$.    Высота трапеции равна   $BH=8$ . В треугольнике   $\bigtriangleup CKD$ проведены высота $KL$ и медиана $KN$. Из вершины $C$ проведена линия $CF$ параллельно боковой стороне $AB$.    Найти много чего!   

• Теорема Фалеса: Параллельные полоски отрезают от секущих пропорциональные отрезки     $\frac{BM}{AM}=\frac{BP}{PH}=\frac{CE}{EF}=\frac{CQ}{QK}=\frac{CN}{ND}$
• Средняя линия треугольника параллельна стороне и равна ее половине:          $QN=\frac{KD}{2}$    $MP=\frac{AH}{2}$      $EQ=\frac{FK}{2}$      $EN=\frac{FD}{2}$
• Средняя линия трапеции    параллельна основаниям и равна их полусумме:      $MN=\frac{BC+AD}{2}$     $MQ=\frac{BC+AD}{2}$       $PN=\frac{BC+HD}{2}$
• Площади фигур: Общее для всех: площадь равна произведению средней линии на высоту!         $S=\frac{a+b}{2} \cdot h$
• Площадь прямоугольника равна произведению длины на ширину    ... умножение сторон:          $S_{HBCK}=BC\cdot BH$
  
• Аддитивность площади:    площадь фигуры равен сумме площадей его частей, кусков.            $S_{ABCD}=S_{ABH}+S_{HBCK}+S_{KCD}$              $S_{HBK}=S_{HBCD}:2$         $S_{FCD}=S_{FCK}+S_{KCD}$            $S_{ABCF}=S_{ABH}+S_{HBCK}-S_{FCK}$
• Медиана на гипотенузу:    прямоугольного треугольника равна половине гипотенузы:         $KN=\frac{CD}{2}$        $HM=\frac{AB}{2}$
• Площадь прямоугольного треугольника равна половине произведения катетов:          $S_{KCD}=\frac{KD\cdot CK}{2}$        $S_{ABH}=\frac{AH\cdot BH}{2}$
• Площадь треугольника равен половине произведения стороны на свою высоту:        $S_{FCD}=\frac{FD\cdot CK}{2}$      $S_{KCD}=\frac{KL\cdot CK}{2}$
• Площадь параллелограмма равна произведению стороны на свою    высоту:           $S_{ABCF}=BC\cdot BH$

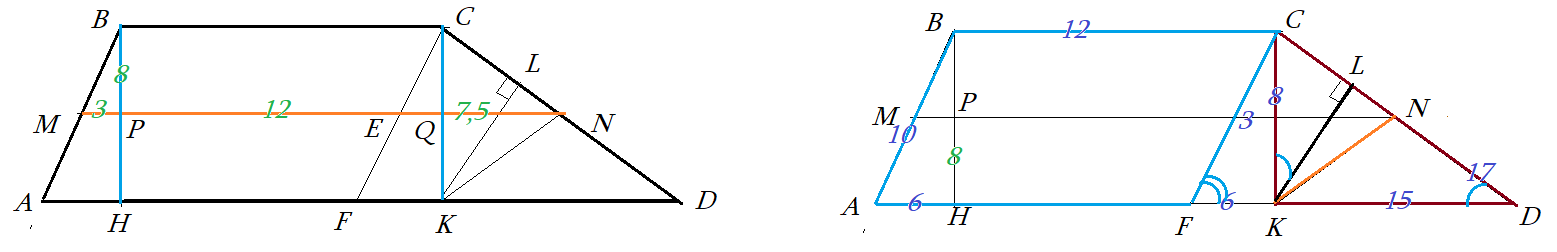
• Подобие прямоугольных треугольников ... хотя бы 1 острый одинаковый:        $\bigtriangleup KCD \sim \bigtriangleup KLD \sim \bigtriangleup KLC$       $\bigtriangleup BPM \sim \bigtriangleup BHA$.
• Тригонометрия углов прямоугольного треугольника: Все прямоугольные с одним и тем же   острым углом подобные!
• $\sin KCD=\frac{KD}{CD}$          $\sin KCD=\frac{KL}{KC}$          $\cos KCD=\frac{KC}{CD}$           $\tg KCD=\frac{KD}{CK}$         $\ctg KCD=\frac{CK}{KD}$          $\cos LKD=\frac{KL}{KD}$
• sin = протиположный : гипотенузу        cos = прилеж : гипотен        tg = протипол : прилеж         ctg = прилеж : протиполож
• Теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы.     $CK^2+KD^2=CD^2$             $KL^2+LN^2=KN^2$
• Основное тождество тригонометрии:        $\sin^2 \angle CDK+\cos^2 \angle CDK=1$              $\sin^2 \angle BAD+\cos^2 \angle BAD=1$
• Высота в прямоугольном делит на подобные, равен средне-геометрическому отрезков гипотенузы     $KL=\sqrt{CL\cdot LD}$
• Площадь треугольника равен половине произведения сторон на синус угла м/д    ними:        $S_{FCD}=\frac{1}{2} \cdot FD \cdot DC \cdot \sin\angle FDC$
• Площадь параллелограмма равна произведению стороны на синус угла м/д ними:           $S_{ABCF}=AB\cdot AF \cdot \sin\angle BAF$
• Теорема косинусов: Связь 3-х сторон и косинуса угла        $CD^2=FC^2+FD^2-2\cdot FC \cdot FD \cdot \cos \angle CFD$
• Тупой угол vs смежный с ним острый:          $\sin \angle CFA=+\sin \angle CFD$             $\cos \angle CFA=-\cos \angle CFD$

Сцена 3:    Дана окружность с центром $O$ и радиусом $r=R=7$. Точки     $A,B,C,D$   на окружности делят всю окружность пропорционально числам 5 : 3 : 2 : 2.   В этих точках проведены касательные к окружности. На рисунке образовались углы, треугольники вписанные и описанные, четыреъугольники вписанные т оптсанные. Найти много чего!   

• Пропорциональное деление    на доли 5 : 3 : 2 : 2 означает, что есть такое $x$, что полученные части равны     $5x$, $3x$, $2x$, $2x$
• Центральный угол угловую меру дуги, которую угол стягивает:                 $\angle AOD=∪AD$              $\angle AOB=∪AB$
• Вписанный угол равен половине угловой меры дуги, на которую угол опирается:       $ \angle BDA=\frac{\cup AB}{2}$             $\angle DAB=\frac{∪DC+∪CB}{2}$
• Радиусы образуют равнобедренные $\bigtriangleup$:    $OA=OB=R$     $OC=OD=R$    $\angle OCB=\angle OBC$
• Окружность описан вокруг 4-х угольника:     равные суммы противоположных углов          $\angle A+\angle C=\angle B+\angle D=180^{\circ}$
• Центр окружности, описанной вокруг    $n$-угольника:    находится на пересечении серединных перпендикуляров. Равноудален!
• Радиус окружности, описанной вокруг $\bigtriangleup ABD$:           $R\cdot 4S_{ABD}=AB\cdot BD\cdot DA$
• Связь радиуса описанной и стороны $\bigtriangleup ABC$:                 $\angle BAC=\frac{\angle BOC}{2}$         $\sin \angle BAC=\frac{0,5BC}{R}$
• Теорема Синусов,        $\bigtriangleup $:                $\frac{\sin \angle BAC}{BC}=\frac{\sin \angle CBA}{CA}=\frac{\sin \angle ACB}{AB}=\frac{1}{2R}$    синусы пропорциональны сторонам напротив.

                  

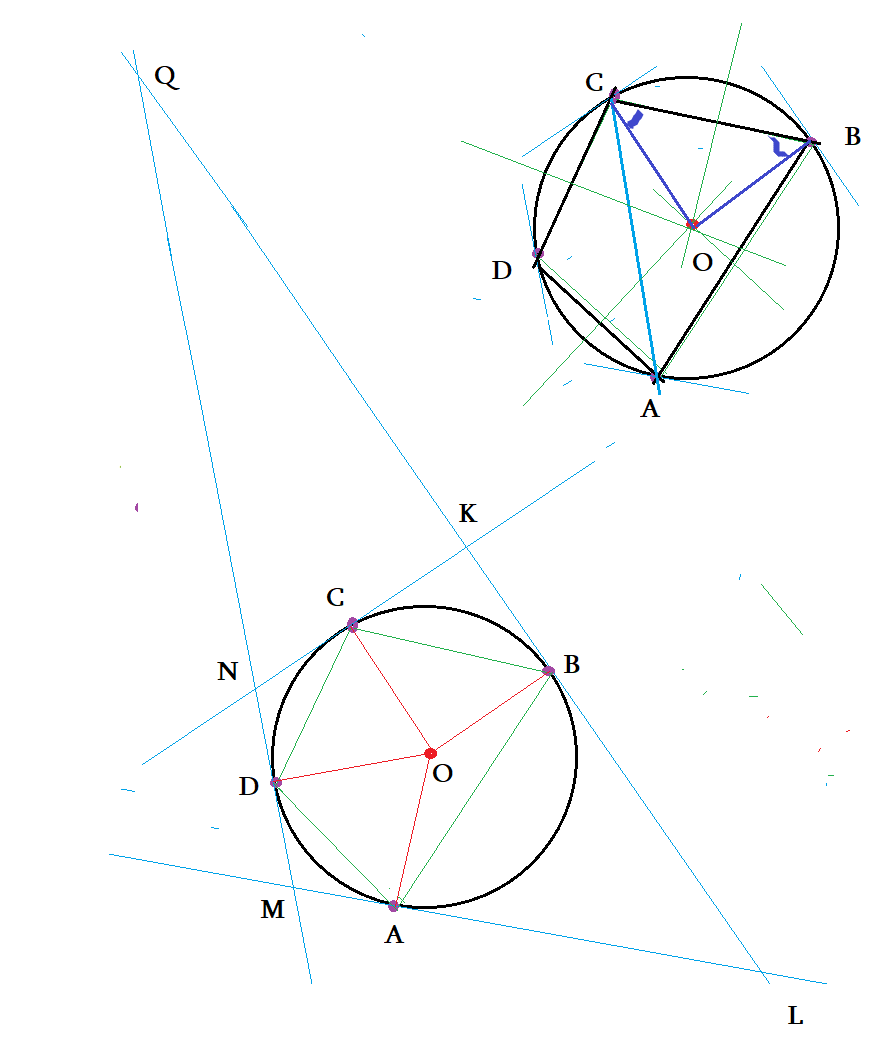
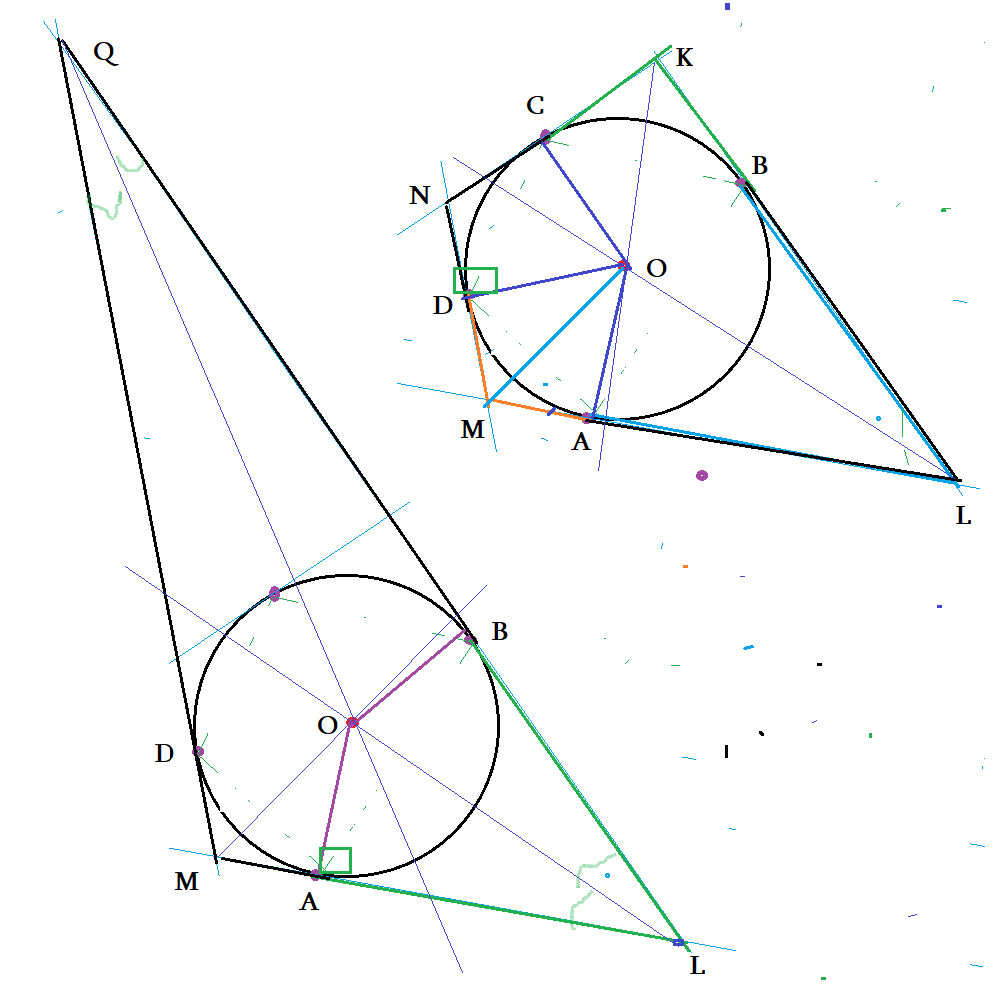
• Обе касательных от точки к окружности    равны:   $LA=LB$        $KC=KB$       $QD=QB$        $\bigtriangleup OMA=\bigtriangleup OMD$
• Касатальная и радиус в точке касания    перпендикулярны:      $OA\perp ML$     $OC\perp NK$   $OB\perp QL$
• Центр вписанной окружности находится на пересечении биссектрис, равноудален от сторон.    $\angle MQO= \angle LQO$
• Радиус вписанной окружности в   $n$-угольник            $r\cdot p_{QML}=S_{QML}$        $r\cdot p_{MNKL}=S_{MNKL}$   полупериметр, площадь
• Окружность вписан в 4-х угольник:       равные суммы противоположных сторон:   $ML+NK=MN+KL$
• Соединение центра с вершинами и точками касания образует несколько пар равных прямоугольних $\bigtriangleup $

Сцена 4:     В трапеции    $ABCD$ основание   $ВС$ и боковая сторона    $CD$ являются касательными к окружности, описанной вокруг треугольника   $ABD$. Найдите площадь треугольника $ABD$, если известно, что     $AD=4\sqrt{3}$ и    $\angle BCD=120^{\circ}$. Боковые стороны продлены до пересечения. Докажите подобия, свойства секущих, хорд, углов.

• Касательные от точки к окружности равны    $CB=CD$ перпендикулярны радиусам   $CB\perp OB$ ,   $CD\perp OD$
• Угол м\д касатальной и хордой равен половине заключенной дуги    $ \angle CBD=\frac{\cup BD}{2}= \angle CDB$
• Одинаковый состав углов приводит к подобию     $\bigtriangleup BCD \sim \bigtriangleup ABD $      $\frac{BD}{AD}=\frac{BC}{AB}$
• Параллельные линии на окружности вырезают равные дуги:              $BC \parallel AB$           $\cup AB=\cup BD$
• Продолжение боковых сторон трапеции образует подобные треугольники         $\bigtriangleup AKD \sim \bigtriangleup BKC $
• Параллельная стороне треугольника отсекает подобный ему $\bigtriangleup $ :           $\frac{AK}{BK}=\frac{DK}{CK}=\frac{AD}{BC}=k$ - коэффициент подобия
• Отношения При Подобиях:        схожие отрезки относятся как   $k:1$;           площади как   $k^2:1$;        схожие   углы $1:1$

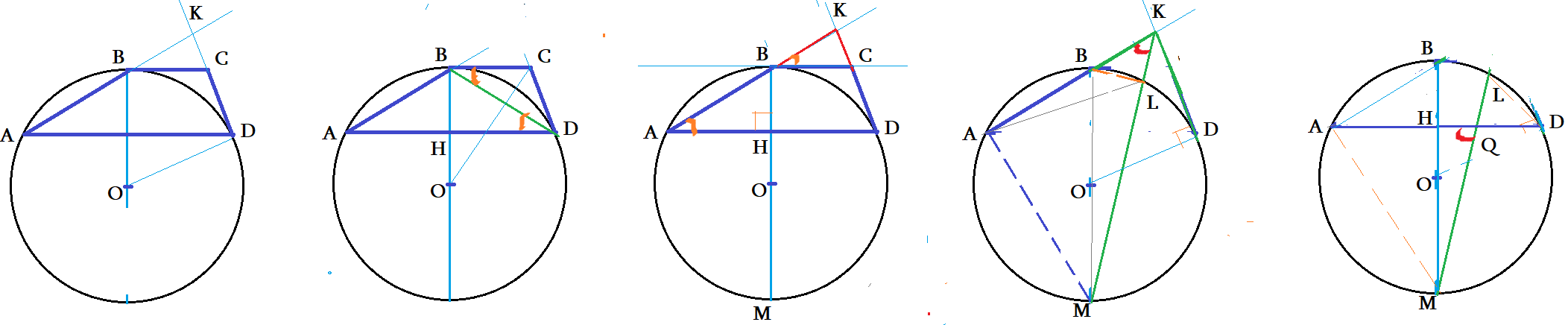
• Две секущих из внешней точки окружности образуют подобные треугольники         $\bigtriangleup KMB \sim \bigtriangleup KAL $
• Внешний угол окружности м\д секущими равен полуразности заключенных дуг     $ \angle AKM=\frac{\cup AM - \cup BL}{2}$
• Произведения отрезков секущих от одной точки равны м\д собой        $KB\cdot KA=KL\cdot KM$
• Квадрат касатальной равен произведению отрезков секущей из то же точки       $KD^2=KB\cdot KA$
• Две пересекающиеся хорды    образуют подобные треугольники           $\bigtriangleup QLD \sim \bigtriangleup QAM $
• Внутрений угол окружности м\д хордами равен полусумме заключенных дуг              $ \angle AQM=\frac{\cup AM - \cup LD}{2}$
• Произведения отрезков пересекающихся хорд    равны м\д собой           $LQ\cdot QM=DQ\cdot QA$ ,           $BH\cdot HM=AH\cdot HD$

Лайфхаки   top - планиметрии

• Отношение площадей подобных $\bigtriangleup $-ов равно   квадрату коэффициента подобия
• Отношение площадей $\bigtriangleup $-ов с одинаковой высотой равен отношению сторон этих высот.
• Отношение площадей $\bigtriangleup $-ов с одинаковым углом равен умножению отношений прилежащих сторон
• Медианы разрезают $\bigtriangleup $ на шесть равных по площади частей.        Каждая медиана делит на 2 равных по площади.

• Площади частей трапеции можно выразить как доли площади всей трапеции через отношения отрезков.
• Отношения отрезков диагоналей в трапеции, параллелограмме выражаются как доли диагоналей через подобия.
• Отношения частей диагоналей, других внутренных отрезков 4-х угольника определяют долю площади частей во всей площади.
• Какова доля $S_{MONK}$ в площади трапеции $S_{ABCD}$ ?    через доли $S_{MON}$ и $S_{MNK}$, через доли частей отрезков.

• Касательная к окружности:     как связан с радиусом, с другим касательным, с секущим?
• Ридиусы образуют равнобедренные $\bigtriangleup $-и: Какие углы равные? Диаметр проходит по середине основания.
• В окружности мало дуго и много углов, реальных и воображаемых, не дорисованных
• Каждая дуга связанна со многоми углами: в окружности полезно искать равные или связанные углы

         

• Есть равные углы?     полезно искать подобные   $\bigtriangleup $-и. Реализовать   подобия!
• подобные $\bigtriangleup $-и приведут к пропорции отрезков. Что из того?
• Из внешней точки выходят секущие? умножения их частей = const.    Искать равные углы.
• Хорды пересекаются?    умножения их частей = const.    Искать равные углы.
• Углы, опирающиеся на диаметр оипраются на полу-окружность, образуют   высоты, катеты.

• Касания окружностей: точка касания лежит на линии центров.    Касание хоть внешнее, хоть изнутри
• Расстояние м\д центрами равен сумме радиусов. Если изнутри, то разности.   $O_{1}O_{2}=R \pm r$
• Общие касательные к обеим окружностям перпендикулярны радиусам, эти радиусы параллельны.
• Касательная, радиусы $r,R$ и отрезок $O_{1}O_{2}$ образуют прямоугольную трапецию. Высота в нем важна!

• Пересечение окружностей:    Соединие точек пересечения перпендикулярно соединению центров.
• Треугольники центров, точек пересечения .... равнобедренные: искать подобнык $\bigtriangleup $-и.
• Соединение центров, точек касания .... искать подобные $\bigtriangleup $-и. Средние линии?
• Полезно: высматривать углы через дуги разных окружностей.

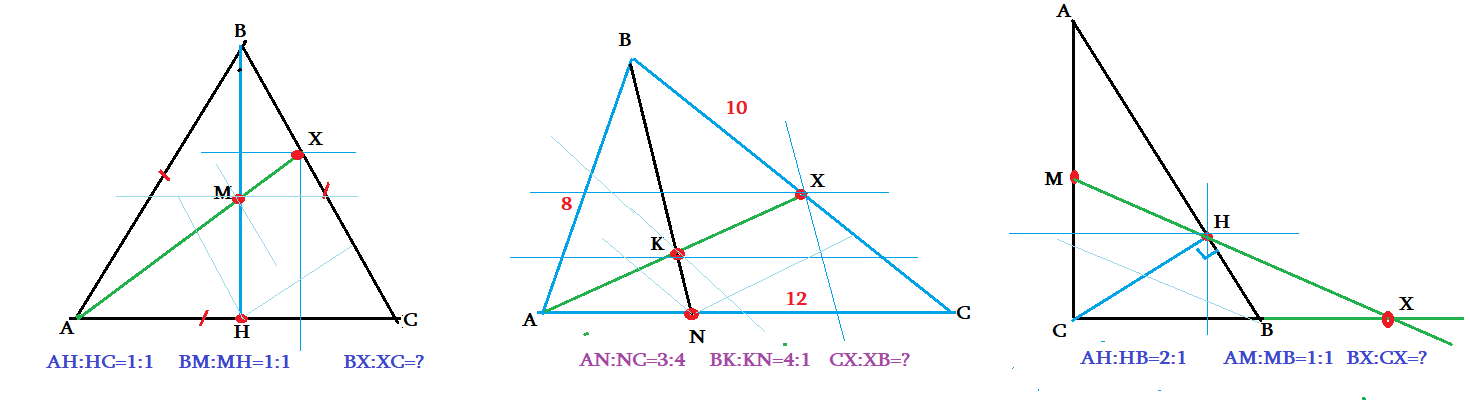
Теорема Менелая:     Неизвестная точка получается на пересечении линий по заданным точкам. Как добраться?

• Проводим параллельные, чтоб использовать известные пропорции.
• Написать   2 - 3    подобия   с выходом, зацепкой неизвестной точки. Поймать точку.

II. Теоремы,          свойства,        формулы

Всё о площадях :

• 1.         У   прямоугольника    площадь   есть   произведение   сторон          $S=a\cdot b$ .
• 2.         У    "параллелограммо - образных"    фигур     (ромб, квадрат, прямоугольник)   площади    находятся   одинаково:
• Формула:               $S=a\cdot h$   -   основание на высоту       ;      ширина на высоту ;    средная линия на высоту
  
• Формула:         $S=a\cdot b\cdot\sin A$   -    сторона   на   сторону и   синус   угла   между   ними.
• 3.         У   "островершинных   фигур"   (треугольник, сектор)    формулы    площади всё те же   ,   но с коэффициентом $1/2$
  2.          $S=\frac{1}{2}ah$    -    так же основание на высоту, но пополам .        Средная линия на высоту.
• 4.         У   сектора   площадь :   длина дуги ("основа") на радиус ("высота") и на $1/2$.     И   площадь окружности всё также 2.          сводится   к площади прямоугольника:   длина полуокружности - как основание прямоугольника, собранного из мелких 2.          секторов раскроенной окружности ,    умноженная   на   радиус , который равен   "высоте" этого прямоугольника.
• 5.         Ну и конечно, надо знать формулу Герона о площади треугольника через   стороны:       $s=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.      
  
• 6.         Не менее важно знать связи площади    с   радиусами   вписанной   и   описанной окружностей:2222222222222222222222222222.                         $s=p\cdot r$         ,         $s=\frac{abc}{4R}$.
• 7.         Архиважно   "чувствовать"   главное    свойство: "площадь целой фигуры равна сложению площадей своих кусков" -2.          это    свойство   аддитивности.
• 8.         Отсюда легко прийти к формуле площади трапеции   -   как гибрида из двух треугольников :          $S=\frac{a+b}{2}h$ -    2.          средняя линия   (как "основание")   на   высоту       
  
• 9.         Также   легко   сконструировать и получить   площадь   любого   четырехугольника         $S=\frac{1}{2}\cdot d_1\cdot d_2\cdot\sin BOC$      -2.          половина произведения диагоналей (как "сторон" некоего треугольника) на синус угла между диагоналями.

Всё   об отношении, сравнении   площадей    фигур :

• Если   треугольники имеют общий   угол, то   несложно   выполнить    сравнение   их   площадей   через   общий   синус.
• Отношение   площадей   треугольников   с   общим   углом   равно   произведению   отношений соответствующих   сторон   этих   треугольников.
  
• Любой   многоугольник   можно   разбить   на   треугольник   и ,таким образом,   выполнять сравнение.
• Площади   подобных   треугольников   относятся   как   квадрат   коэффициента   подобия.
• Если   треугольники   имеют   одинаковые    высоты, то   их    площади   относятся   как   основания.      
  
• Медиана   треугольника    делит   его на   равновеликие    треугольники,   отношение   площадей   $1:1$ .
• Диагонали   трапеции   образуют   4 треугольника:   отношение площадей   боковых   $1:1$ ;
• отношение   площадей у оснований   равно отношению самих   оснований.
  

Об углах и отрезках окружности:   теоремы и свойства хорд, секущих и касательных

• Градусная мера дуги окружности - градусная мера соответствующего центрального угла.
• Вписанный Угол   равен половине соответствующего центрального угла, половине дуги опирания.
• Все вписанные углы, опирающиеся на одну и ту же дугу, равны меж собой.
• Вписанные углы, опирающиеся на диаметр, равны 90 градусов (прямой угол).
• Угол при пересечении хорд половина сумм дуг опирания. (внутренный угол окружности).      
  
• При пересечении двух хорд возникают подобные треугольники, произведения отрезков одинаковые.
  
• Теорема: "Произведение отрезков каждой из двух пересекающихся хорд есть величина постоянная".
• Угол между секущими равен половине разности дуг, заключенных между секущими. (внешный угол).      
  
• Теорема: "Произведения отрезков секущих одинаковы для всех секущих, проведенных из одной точки".
• Произведение отрезков секущих до 1-ой и 2-ой точек пересечения с окружностью - постоянная".
• Теорема: "В точке окружности проведенная касательная и радиус в точке касания перпендикулярны".
• Теорема: "Квадрат касательной равен произведению отрезков секущей, проведенной из той же точки".
• Угол между касательной и хордой в точке касания равен половине градусной меры заключенной между ними дуги.

Теоремы и факты о вписанной окружности (в угол, в треугольник, в четырехугольник):

• Биссектриса - геометрическое место точек, равноудаленных от обеих сторон угла.
  
• Центр окружности, вписанной в угол находится в точке, принадлежащей биссектрисе (равноудалена ...)
• Центр вписанной окружности в треугольник - на пересечении биссектрис.
• Центр вписанных окружностей в любую фигуру - на пересечении биссектрис. Центр равноудален от сторон.
• Радиус к точке касания стороны перпендикулярен стороне (сторона является касательной к окружности).      
  
• Точки касания делят стороны на попарно равные отрезки (касательные из вершины многоугольника).
• Радиус $r$   вписанной (в треугольник, четырехугольник, многоугольник) окружности:     $r=\frac{S}{p}$     ,        $S=p\cdot r$.
  
• "О вписанной в четырехугольник окружности":   можно вписать тогда и только тогда, когда суммы
                            противоложных сторон четырехугольника равны    $a+c=b+d$.

Теоремы и факты об описанной окружности вокруг двух точек, треугольника, четырехугольника:

• Серединный перпендикуляр отрезка - геометрическое место точек, равноудаленное от двух точек .
  
• Центр описанной окружности находится на пересечении серединных перпендикуляров, проведенных к сторонам.
• Центр описанной окружности равноудален   от вершин   треугольника, многоугольника .
• Радиус   $R$    описанной вокруг треугольника окружности:     $R=\frac{a\cdot b\cdot c}{4\cdot S}$   ;     $S=\frac{a\cdot b\cdot c}{4\cdot R}$ .
• Теорема   Синусов:    $ \frac{\sin\angle A}{a}=\frac{1}{2R}$      ;          $\frac{\sin\angle B}{b}=\frac{1}{2R}$      ;           $\frac{\sin\angle C}{c}=\frac{1}{2R}$ .      
  
• Вокруг четырехугольника окружность можно описать тогда и только тогда ,   когда   суммы
              противоложных углов четырехугольника равны 180 градусов.     $\angle A+\angle C=180=\angle B+\angle D$

I.    Треугольники, Четырехугольники.      Задачи из Задания №16     ЕГЭ - профиль

II. Вписанные, Описанные окружности.      Задачи из Задания №16     ЕГЭ - профиль

III. Окружности: хорды, секущие, касательные.    Задачи из Задания №16     ЕГЭ - профиль

IV. Окружности и фигуры. Задачи из Задания №16     ЕГЭ - профиль

V. Две, три окружности.     Задачи из Задания №16     ЕГЭ - профиль

_Задачи №1 - №8:    можно решать в интерактивном режиме,

№1. В треугольнике ABC известны стороны AB  =  4, AC  =  5 и На его стороне BC вне треугольника (точки A и D лежат в разных полуплоскостях относительно прямой BC) построим равносторонний треугольник BCD.   а)  Докажите, что около четырёхугольника ABDC можно описать окружность.   б)  Найдите расстояние от центра этой окружности до точки пересечения диагоналей четырёхугольника ABDC.

№2. Внутри окружности с центром О построен правильный шестиугольник KOFPDL так, что его вершина D лежит на окружности. Из точки В, диаметрально противоположной точке D, проведены две хорды AB и ВС, проходящие через вершины К и F шестиугольника соответственно.   а)  Докажите, что AK : KB = 3 : 7 б)  Найдите площадь треугольника АВС, если радиус окружности равен 14.

№3 Окружность, вписанная в треугольник ABC, делит медиану BM на три равные части.   а)  Докажите, что BC : CA : AB  =  5 : 10 : 13.   б)  Найдите радиус вписанной окружности, если BM  =  12.     ------ задача 43: интерактив работает не полноценно!!!!!!!

№4 Окружность проходит через вершины   A, B и C параллелограмма и пересекает продолжение стороны AD в точке E, а продолжение стороны CD в точке в K.       а)  Докажите, что отрезки BE и BK равны.   б)  Найдите отношение KE к AC, если   $\angle ABC=135$

№5 К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. а)  Докажите, что периметр треугольника AMN равен стороне квадрата.   б)  Прямая MN пересекает прямую CD в точке P. B каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 4

№6 Четырехугольник ABCD с перпендикулярными диагоналями AC и BD вписан в окружность.   а)  Докажите, что прямая, проходящая через точку пересечения диагоналей четырехугольника перпендикулярно стороне BC, делит пополам сторону AD.   б)  Найдите стороны четырехугольника ABCD, если известно, что AC  =  84 и BD  =  77, а диаметр окружности равен 85.

№7 Сторона AB квадрата ABCD равна 1 и является хордой некоторой окружности, причем остальные стороны квадрата лежат вне этой окружности. Длина касательной CK, проведенной из вершины C к этой окружности, равна 2.     а)  Докажите, что длина отрезка, соединяющего центр квадрата и центр окружности равна длине отрезка CK.    б)  Найдите диаметр окружности.

№8 Дан треугольник ABC со сторонами AC  =  6, BC  =  8 и AB  =  10. Вписанная в него окружность с центром I касается стороны BC в точке L, M  — середина BC, AP  — биссектриса треугольника ABC, O  — центр описанной около него окружности.    а)  Докажите, что P  — середина отрезка LM.     б)  Пусть прямые OI и AC пересекаются в точке K, а продолжение биссектрисы AP пересекает описанную окружность в точке Q. Найдите площадь четырёхугольника OKCQ.

№9 На окружности с центром O и диаметром MN, равным 34, взята точка K на расстоянии 15 от этого диаметра. Хорда KE пересекает радиус OM в точке F под углом, равным   $\arccos \frac{4}{5}$.      а)  Докажите, что     $\frac{KF}{FE}=\frac{125}{29} . б)  Найдите площадь $s$ треугольника KEN.

№10 В треугольник ABC вписана окружность радиуса 4, касающаяся стороны AC в точке M, причём AM=8 и CM=12. а) Докажите, что треугольниk ABC прямоугольный.   б) Найдите расстояние между центрами вписанной и описанной окружностей треугольника ABC.

№11 Четырёхугольник ABCD вписан в окружность радиусом 10. Известно, что   AB=BC=CD=6.    а) Докажите, что прямые BC и AD параллельны.   б) Найдите AD.

№12 В треугольнике ABC известно, что AB=AC=15, BC=18. На стороне AB отметили точки M1 и M2 так, что AM1<AM2. Через точки M1 и M2 провели прямые, перпендикулярные стороне AB и отсекающие от треугольника ABC пятиугольник, в который можно вписать окружность.   а)   Докажите, что AM1:BM2=1:3.   б) Найдите площадь s данного пятиугольника.

№13   Дан прямоугольный треугольник АВС с прямым углом С. На катете АС взята точка М. Окружность с центром О и диаметром СМ касается гипотенузы в точке N.   а) Докажите, что прямые MN и ВО параллельны.   б) Найдите площадь четырехугольника BOMN, если CN=8,   AM:MC=1:3.

             

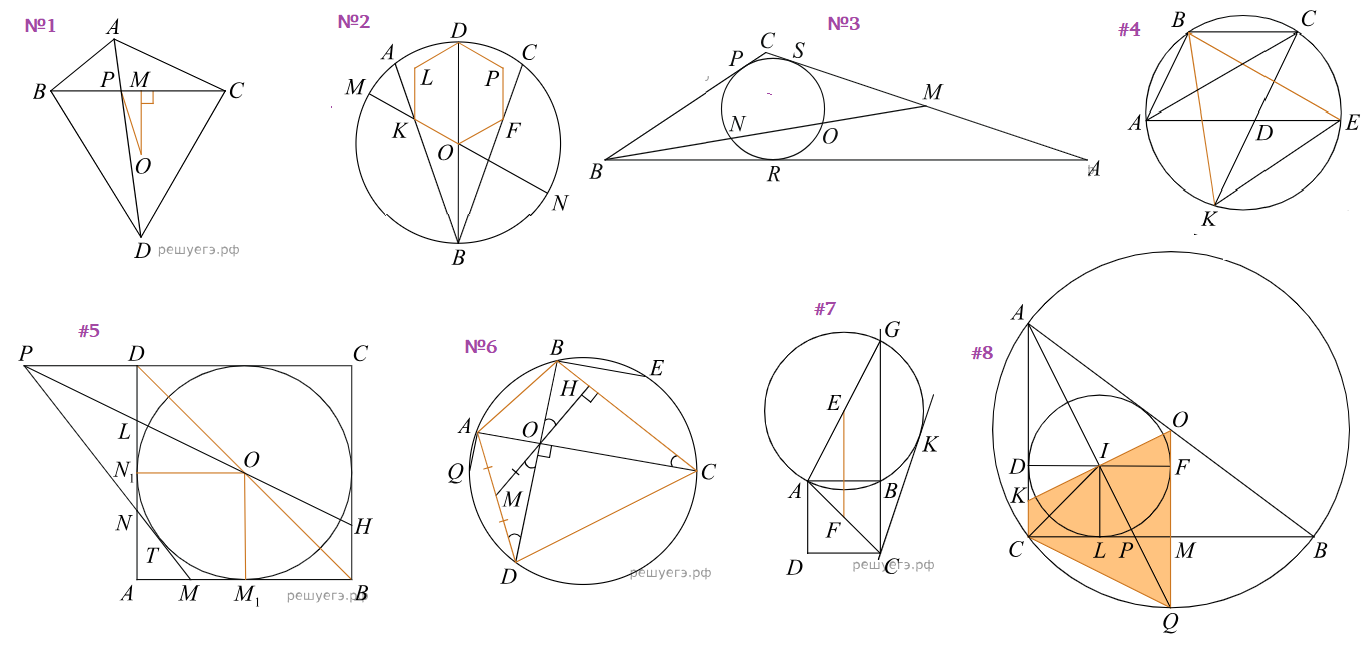
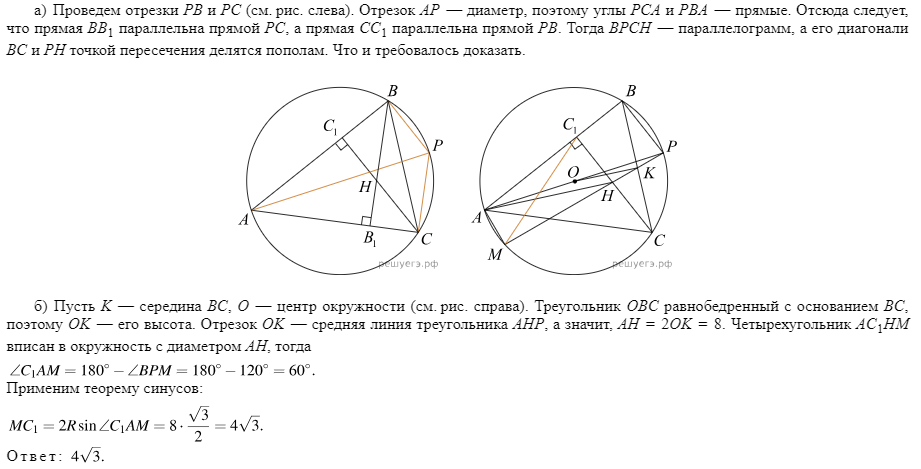
№14   Высоты $BB_1$ и $CC_1$ остроугольного треугольника $ABC$ пересекаются в точке H. Отрезок AP  — диаметр окружности, описанной около треугольника ABC. а)  Докажите, что прямая HP пересекает отрезок BC в его середине. б)  Луч $PH$ вторично пересекает окружность, описанную около треугольника ABC, в точке M. Найдите длину отрезка $MC_1$, если расстояние от центра этой окружности до прямой BC равно 4,      $\angle BPH=120$.