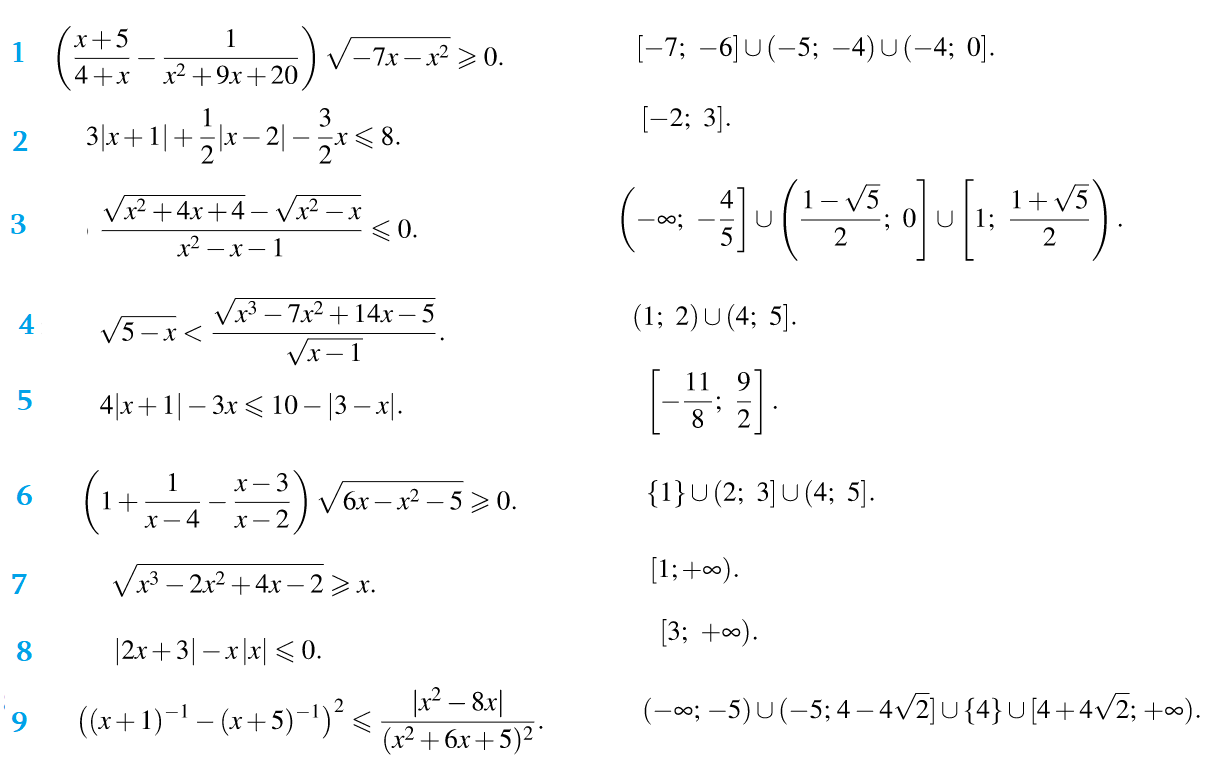III. Метод рационализации
Стратегия: вместо логарифмического неравенства иногда удобнее решать его рационализованный аналог - методом интервалов, путем нахождения критических точек обнуления множителей и делителей . Сравнение разности логарифмов с нулем эквивалентно Сравнению дробно-рационального с нулем!
Рационализация разности степеней: Знак выражения $a^B-a^C$ совпадает со знаком $\frac{B-C}{a-1}$ дробного.
Метод рационализации показательных неравенств: $a^B-a^C < 0$ и $\frac{B-C}{\left(a-1\right)} < 0$ имеют одинаковые решения.
Рационализация разности логарифмов: Знак выражения $\log_aB-\log_aC$ совпадает со знаком $\frac{B-C}{a-1}$ дробного. при (ОДЗ).
Метод рационализации неравенства с логарифмами: $\log_aB-\log_aC > 0$ и $\frac{B-C}{\left(a-1\right)} > 0$ имеют одинаковые решения. При (ОДЗ).
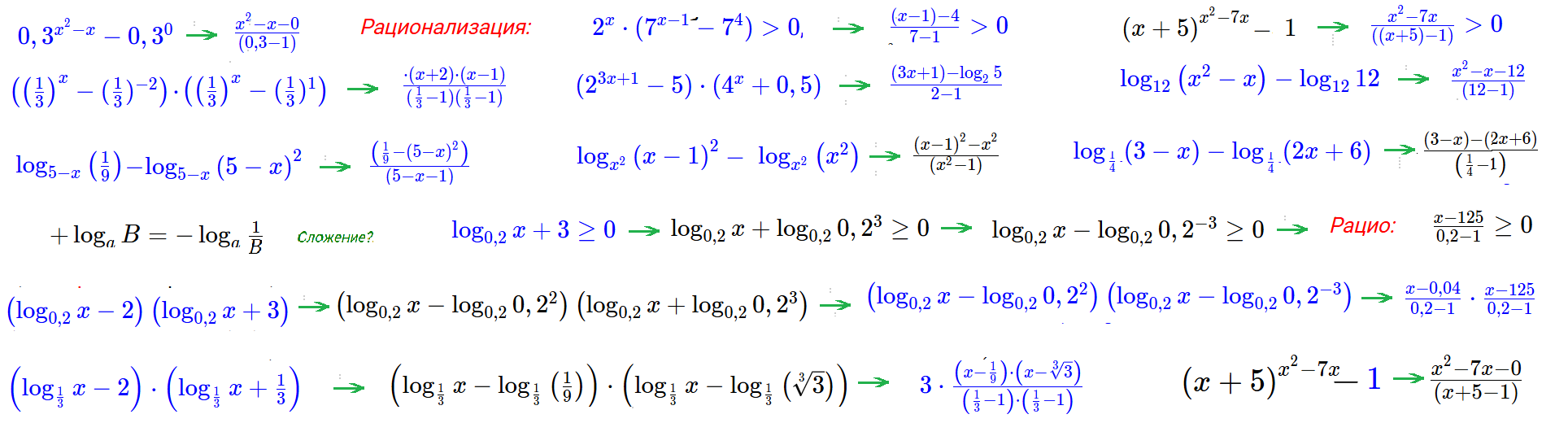
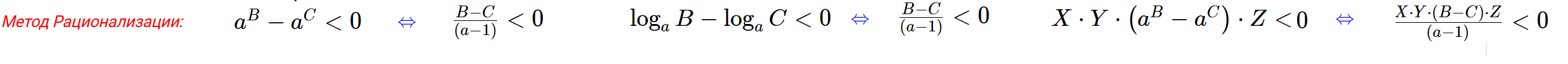
Метод рационализации неравенств: Превратить в сравнение с 0. Рационализировать разности логарифмов / степеней.
Теорема эквивалентности: знака разности степеней (логарифмов) со знаком разности их показателей (аргументов):.
- Знак разности $a^B-a^C$ ($\log_aB-\log_aC$) совпадает со знаком $\frac{B-C}{a-1}$ при любых $a > 0$, $a\ne1$
- Сравнение с нулем разности $a^B-a^C\le0$ ($\log_aB-\log_aC$) равносильно со сравнением с нулем выражения $\frac{B-C}{a-1}\le0$
- Сравнение разности степеней (логарифмов) с 0 $\Leftrightarrow$ "сравнение разности показателей (лог) :$(a-1)$) с 0" с тем же знаком.
- ${a-1}$ в знаменателе $\frac{B-C}{a-1}$ гарантирует правильный учет для обеих ситуаций с "основание больше или меньше 1".
- Метод Рационализации: неравенство $a^B-a^C\le0$ $\Leftrightarrow$ $\frac{B-C}{a-1}\le0$ - рациональный аналог.
Особыe Рационализации: одинокий логарифм $\log_aB$ $\to$ $\log_aB-0$ $\to$ $\log_aB-log_a1$ $\to$ $\frac{B-1}{a-1}$
Сумма логарифмов $\log_aB+\log_aC$ $\to$ $\log_aB-\log_a{\frac{1}{C}}$ $\to$ $\frac{B-\frac{1}{C}}{a-1}$ ... сумму Лог превратить в разность Лог!
Не надо, ибо положительно: ( $\to$ $+1$): Одинокая степень ${0,3}^{f(x)}>0$ ; Степень + число $2^{x-1}+3>0$; Сумма степеней $2^{x-1}+3^x>0$

III. Метод факторизации и дальнейщей рационализации
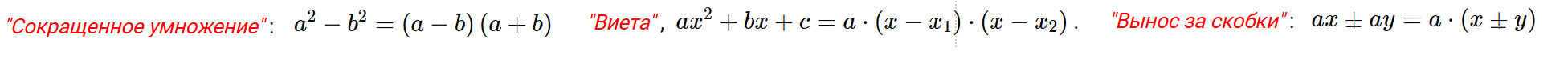
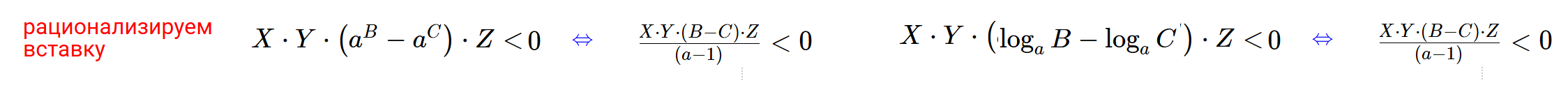
Примеры решения неравенств: факторизация, рационализация:.
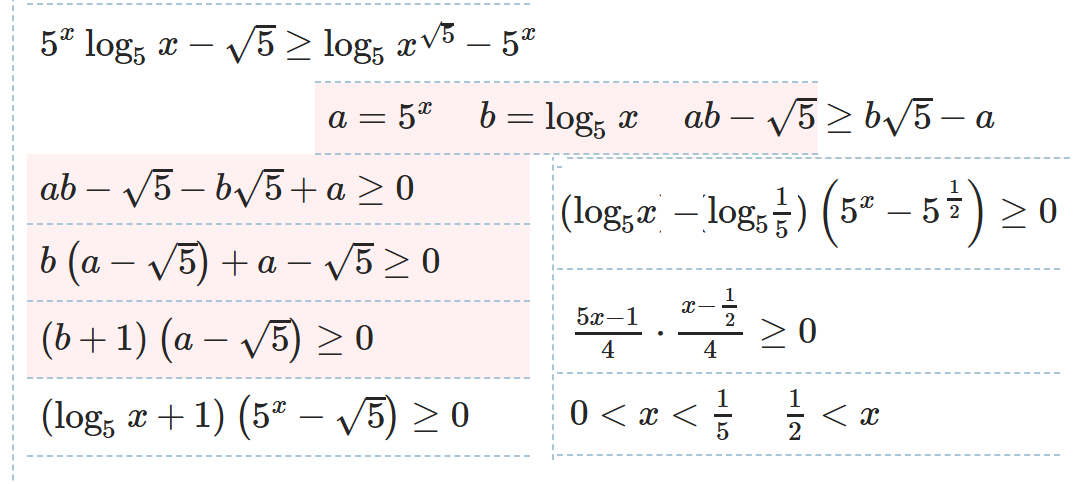
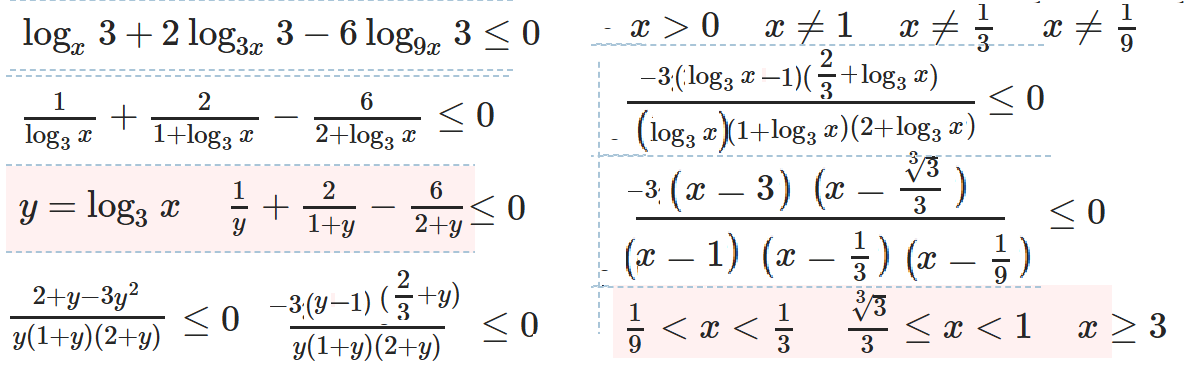
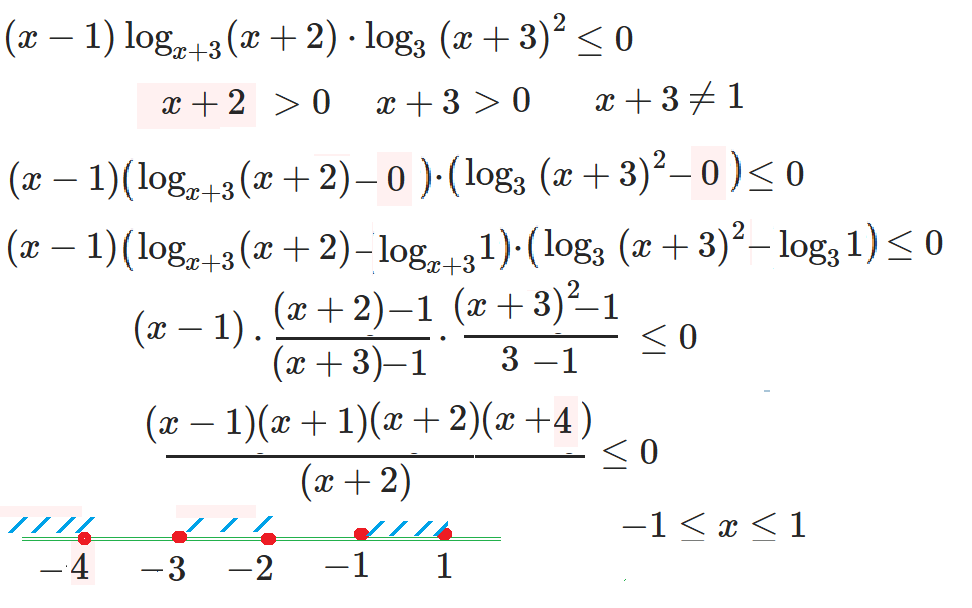

III. Факторизация и рационализация сложных неравенств
Примеры Замен для факторизации:
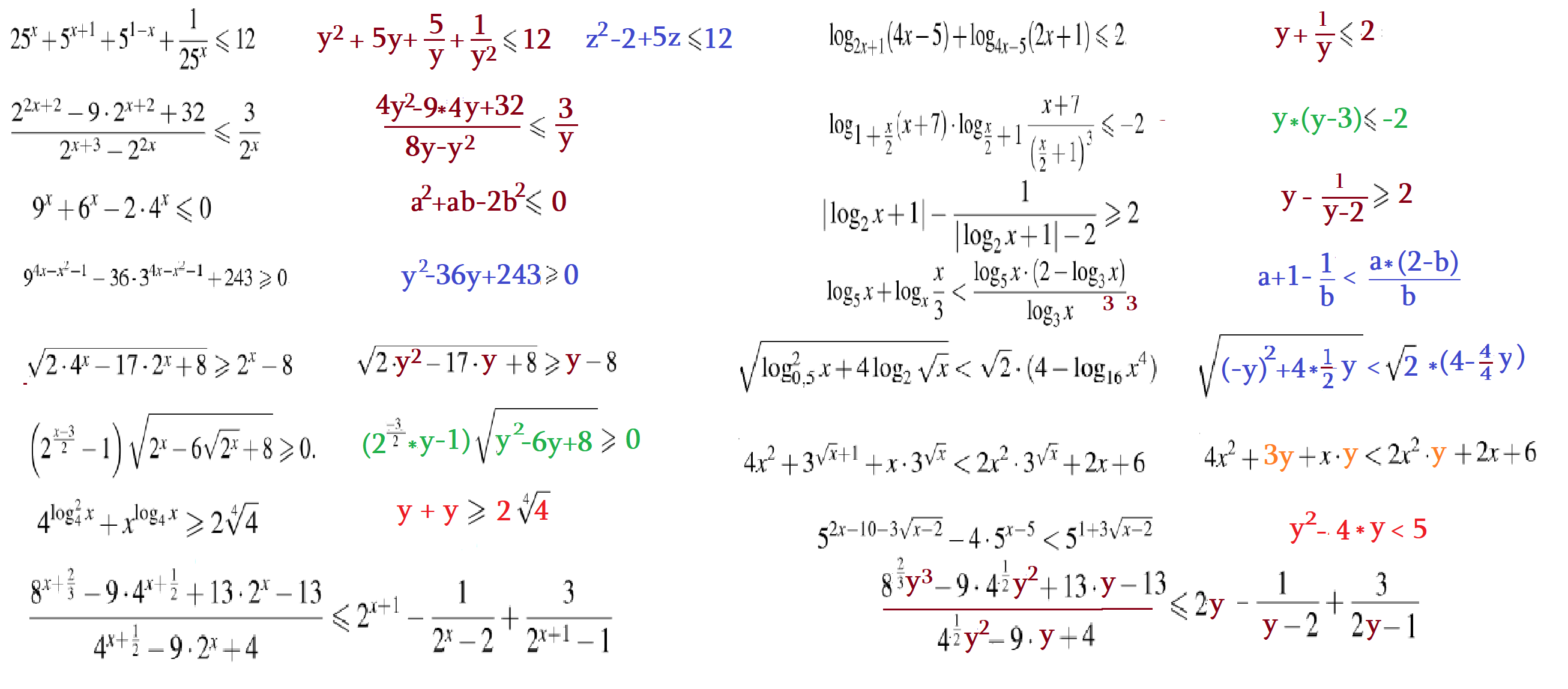
Задача 1: Решите неравенство $\frac{\log_{2x}{\left(3x-1\right)}\cdot \log_{3x}{\left(2x-1\right)}}{2^x-4}\ge 0$
- ОДЗ условия: $2x>0$ $2x\ne 1$ $3x-1>0$ $3x>0$ $3x\ne 1$ $2x-1>0$ $2^x-4\ne 0$
- $x\in \left(\frac{1}{2};2\right)$ $x\in \left(2;+\infty \right)$ . Интервалы ОДЗ. В другом виде: $\frac{1}{2} < x$ $ <2$ $x>2$
- $\frac{\frac{\left(3x-1\right)-1}{2x-1}\cdot \frac{\left(2x-1\right)-1}{3x-1}}{\frac{x-2}{2-1}}\ge 0$ Рационализация множителей\делителей: $\frac{A\cdot B}{C}\ge 0$ $\Leftrightarrow$ $\frac{R_A\cdot R_B}{R_C}\ge 0$
- $\log_{2x}(3x-1) \to (\log_{2x}(3x-1)-0) \to (\log_{2x}(3x-1)-\log_{2x}(1) \to \frac{\left(3x-1\right)-1}{2x-1}$ ... Рацио одинокого Лог.
- $\Rightarrow$ $\frac{\left(3x-2\right)\cdot \left(2x-2\right)}{\left(x-2\right)\cdot \left(2x-1\right)\cdot \left(3x-1\right)}\ge 0$ ... Решаем дробное неравенство.
- $........\left(+\frac{1}{3}\right) ........\left(\frac{1}{2}\right)........\left(\frac{2}{3}\right)........\left(1\right)........\left(+2\right)........$ Числовая ось: отметим корни.
- $-\left(+\frac{1}{3}\right)+\left(\frac{1}{2}\right)-\left(\frac{2}{3}\right)+\left(1\right)-\left(+2\right)+$ - Знаки на интервалах, проверка неравенства.
- $\frac{1}{3} < x < \frac{1}{2}$ $\frac{2}{3}\le x\le 1$ $x>2$ - Решение неравенства, без учета ОДЗ.
- Ответ: $\frac{2}{3}\le x\le 1$ $x>2$ - пересечение решений неравенства с интервалами ОДЗ.
Задача 2: Решите неравенство $\sqrt{x^2-4}\cdot 4^{\frac{1}{x}-1}\le 2^{\frac{1}{x}-2}\cdot \sqrt{x^2-4}+\sqrt{9x^2-36}$
- ОДЗ: $\sqrt{x^2-4}\ge 0$ $\Leftrightarrow$ $x\le -2$ , $x\ge 2$ -
- Замена: $a=\sqrt{x^2-4}$ ; $b=2^{\frac{1}{x}}$ $\Rightarrow$ $2^{\frac{1}{x}-2}=\frac{b}{4}$ , $4^{\frac{1}{x}-1}= \frac{b^2}{4}$ , $\sqrt{9x^2-36}=3a$
- $a\cdot \frac{b^2}{4}\le \frac{b}{4}\cdot a+3a$ уравнение подстановки, разложим на множители ...
- $\Leftrightarrow$ $a\cdot \frac{b^2-b-12}{4}\le 0$ $\Leftrightarrow$ $a\cdot (b+3) \cdot (b-4)\le 0$ факторизация - произведение в сравнении с 0
- $\sqrt{x^2-4}\cdot (2^{\frac{1}{x}}+3) \cdot (2^{\frac{1}{x}}-4)\le 0$ ; Положительность: $\sqrt{x^2-4}\ge 0$ $2^{\frac{1}{x}}+3>0$
- $\sqrt{x^2-4}=0$ $\Leftrightarrow$ $x=-2$ , $x=2$ одинокое решение неравенства.
- $\Rightarrow$ $2^{\frac{1}{x}}-4\le 0$ $\Leftrightarrow$ $\frac{\frac{1}{x}-2}{2-1}\le 0$ Рационализация
- $\frac{1-2x}{x}\le 0$ $\Leftrightarrow$ $x\le 0$ , $x\ge \frac{1}{2}$ ... Решение неравенства
- $x\le -2$ , $x\ge 2$ пересечение решений неравенства с интервалами ОДЗ.
Задача 3: Решите неравенство $\frac{64^x}{36^x-27^x}+\frac{4(16^x-12^x)}{16^x-2\cdot 12^x+9^x}\le \frac{3\cdot 4^{2x}}{12^x-9^x}$
- ОДЗ: $36^x-27^x\ne0$, $16^x-2\cdot 12^x+9^x\ne0$, $12^x-9^x\ne0$ $\Leftrightarrow$ $x\ne0$
- $a=4^x$ , $b=3^x$ замены:: $64^x=a^3$ , $16^x=a^2$ , $9^x=b^2$, $27^x=b^3$ , $12^x=(4\cdot 3)^x=a\cdot b$ , $4^{2x}=a^2$
- $\frac{a^3}{ab^2-b^3}+\frac{4(a^2-ab)}{a^2-2ab+b^2}\le \frac{3a^2}{ab-b^2}$ Неравенство подстановки. Факторизуем:
- $\frac{a^3}{b^2(a-b)}+\frac{4a(a-b)}{(a-b)^2}\le \frac{3a^2}{b(a-b)}$ $\Leftrightarrow$ $\frac{a^3}{b^2(a-b)}-\frac{4a}{a-b}-\frac{3a^2}{b(a-b)}\le 0$
- $\frac{a^3-4ab^2-3a^2b}{b^2(a-b)}\le 0$ $\Leftrightarrow$ $\frac{a(a^2-4b^2-3ab)}{b^2(a-b)}\le 0$ превратим произведение $\le 0$ ... Виета разложением
- $\frac{a(a-4b)(a+b)}{b^2(a-b)}\le 0$ $\Leftrightarrow$ Возвратное факторизованное: $\frac{4^x\cdot (4^x-4\cdot 3^x)(4^x+3^x)}{(3^x)^2(4^x-3^x)}\le 0$
- Отделим и отбросим заведомо положительные $4^x>0$ , $4^x+3^x>0$ , $(3^x)^2>0$
- $\frac{4^x\cdot (4^x+3^x)}{(3^x)^2}\cdot \frac{4^x-4\cdot 3^x}{4^x-3^x}\le 0$ $\Leftrightarrow$ $\frac{4^x-4\cdot 3^x}{4^x-3^x}\le 0$ сократим на $3^x$ числитель и знаменатель
- $\frac{(\frac{4}{3})^x-4}{(\frac{4}{3})^x-1}\le 0$ рационализируем, с учетом: $\frac{4}{3}-1>0$ , $4=(\frac{4}{3})^{\log_{\frac{4}{3}}4}$ , $1=(\frac{4}{3})^0$
- $\frac{x-\log_{\frac{4}{3}}4}{x-0}\le 0$ дробное, $\Leftrightarrow$ $\frac{x-\frac{1}{\log_{4}{\frac{4}{3}}}}{x-0}\le 0$ $\Leftrightarrow$ $\frac{x-\frac{1}{1-\log_43}}{x}\le 0$
- $\log_43\approx 0.8$ $\to$ $\frac{1}{1-\log_43}>1$ ; решение неравенства: $0<x \le \frac{1}{1-\log_43}$
Задача 4: Решение неравенств:
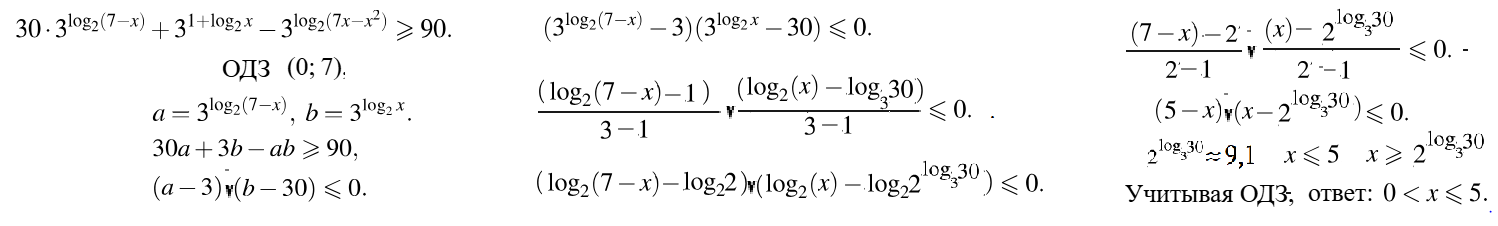
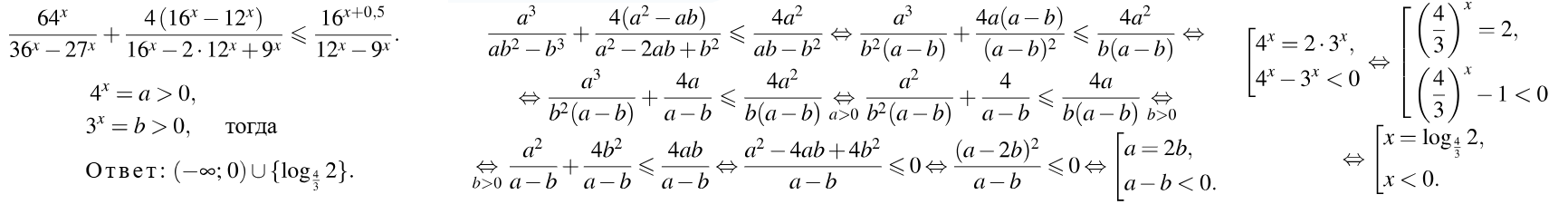
- Внимание: Урок, теорию о рационализации степенных смотри здесь, VII . § 20. Метод Рационализации в Степенно-Показательных Неравенствах
Теорема: эквивалентность знака разности степеней со знаком разности их показателей.
- Знак разности степеней $a^B-a^C$ совпадает со знаком $\frac{B-C}{a-1}$ при любых $a > 0$, $a\ne1$
- Сравнение с нулем разности степеней $a^B-a^C\le0$ равносильно со сравнением с нулем выражения $\frac{B-C}{a-1}\le0$
- "Сравнение разности степеней с 0" $\Leftrightarrow$ "сравнение разности показателей (:$(a-1)$) с 0" с тем же знаком.
- ${a-1}$ в знаменателе $\frac{B-C}{a-1}$ гарантирует правильный учет для обеих ситуаций с "основание больше или меньше 1".
- Метод Рационализации: неравенство $a^B-a^C\le0$ $\Leftrightarrow$ $\frac{B-C}{a-1}\le0$ - рациональный аналог.
Пример 1: Решить показательное неравенство $1,3^{x^2-x} < 1$
- Перепишем как "сравнение разности степеней с 0": $1,3^{x^2-x} < 1,3^0$ $1,3^{x^2-x}-1,3^0 < 0$
- Метод Рационализации: $1,3^{x^2-x}-1,3^0 < 0$ $\Leftrightarrow$ $\frac{x^2-x-0}{\left(1,3-1\right)} < 0$
- Решаем рациональное неравенство, разложим на множители $\frac{\left(x+0\right)\left(x-1\right)}{0,3} < 0$
- Метод интервалов: критические точки 0 и 1 - точки обнуления множителей и делителей.
- Выберем контрольные точки на всех интервалах ( -10; 0.5; 10 ) и проверим неравенство - знаки внутри скобок.
- Для $x=0,5$ выполняется $\frac{\left(+\right)\left(-\right)}{\left(+\right)} < 0$. При -10 и 10 не выполняется. ответ $ 0 < x < 1$
Пример 2: Решить сложно-степенное неравенство $\left(x+5\right)^{x^2-7x} > 1$
- сложно-степенное выражение, функция - степень, переменная находится и в основании, и в показателе.
- ОДЗ: $x+5>0$ , $x+5\ne1$ - основание сложно-степенного выражения объязано быть > 0, и не равно 1.
- Представим правую часть как степень с основанием $x+5$, получим $\left(x+5\right)^{x^2-7x} > \left(x+5\right)^0$
- Перенесем все влево, чтоб "разность сравнивался с 0": $\left(x+5\right)^{x^2-7x}-\left(x+5\right)^0 > 0$
- Рационализируем разность, перейдем к сравнению разности показателей с 0 : $\frac{x^2-7x-0}{\left(x+5-1\right)} > 0$
- Упростим, решаем дробно-рациональное неравенство $\frac{x^2-7x}{\left(x+4\right)} > 0$ $\Leftrightarrow$ $\frac{x\left(x-7\right)}{x+4} > 0$
- Метод интервалов: критические точки $0$, $7$, $-4$ от неравенства и $-5$, $-4$ от ОДЗ.
- Критические точки $-5 < -4 < 0 < 7$ ; контрольные точки: $-10$; $-4,5$; $-2$; $3$; $10$. Проверка знаков.
- Все проверки приведут к решениям, интервалам: ответ $-4 < x < 0$ $x > 7$
Пример 3: Решить неравенство $3\cdot\left(\frac{1}{3}\right)^{2x}-28\cdot\left(\frac{1}{3}\right)^x+3\le0$
- Как бы решали уравнение, = 0? Методом замены. Также и здесь, но с ньюансом "возврата":
- Метод Замены: $y=\left(\frac{1}{3}\right)^x$ $3y^2-28y+3\le0$
- ... Найдем корни $y_1=9$ $y_2=\frac{1}{3}$ ... разложим по "Виета" .... сделаем "возврат"
- $3\cdot\left(y-9\right)\cdot\left(y-\frac{1}{3}\right)\le0$ $\Leftrightarrow$ $3\cdot\left(\left(\frac{1}{3}\right)^x-9\right)\cdot\left(\left(\frac{1}{3}\right)^x-\frac{1}{3}\right)\le0$
- Теперь главное , каждую скобку отдельно "рационализируем" : заменим разности степеней ...
- $3\cdot\left(\left(\frac{1}{3}\right)^x-\left(\frac{1}{3}\right)^{-2}\right)\cdot\left(\left(\frac{1}{3}\right)^x-\left(\frac{1}{3}\right)^1\right)\le0$ $\Leftrightarrow$ $3\cdot\frac{\left(x-\left(-2\right)\right)\cdot\left(x-1\right)}{\left(\frac{1}{3}-1\right)\left(\frac{1}{3}-1\right)}\le0$
- Цель достигнута: вместо показательного получили дробно-рациональное $\frac{27\cdot (x+2)\cdot (x-1)}{4}\le0$
- Расставим критические точки в порядке возрастания: -2 и 1 . Получим интервалы разбиения;
- Проанализируем знаки на контрольных точках каждого интервала: ответ $-2\le x\le1$
Алгоритм: "Метод рационализации неравенства со степенями".
-
Шаг 1: Превращаем неравенство к виду разность степеней сравнить с 0 : $a^B-a^C<0$
-
Шаг 2: Решаем рационализированное неравенство $\frac{B-C}{\left(a-1\right)} < 0$
-
Дополнение: Если неравенство имеет вид $X\cdot Y\cdot\left(a^B-a^C\right)\cdot Z < 0$ с некими выражениями $X$, $Y$ , $Z$ ... то
-
рационализируем вставку и решаем $\frac{X\cdot Y\cdot\left(B-C\right)\cdot Z}{\left(a-1\right)} < 0$ . Если есть еще вставка, то и ее "рационализируем".
Причина: вместо неравенства со степенями удобнее решать его рационализованный аналог - методом интервалов, путем нахождения критических точек обнуления множителей.
Замечание: В неравенствах очень важно то, что "произведение сравнивается с нулем". Для уравнений это приводило к разбиению на случаи : какой либо множитель должен стать нулем. В неравентствах вида "слева произведение или деление <> справа 0 " нам достаточно знать знаки множителей / делителей чтоб понять - выполняется ли <сравнение> с нулем.
Способы разложения на множители: "Виета" , разложение квадратного по корням: $ax^2+bx+c=a\cdot\left(x-x_1\right)\cdot\left(x-x_2\right)$ . "Сокращенное умножение" : разложение разности квадратов $a^2-b^2=\left(a-b\right)\left(a+b\right)$ "Вынос за скобки" : $ax^2-bx=x\cdot\left(ax-b\right)$ $ax+ay=a\cdot\left(x+y\right)$
Пусть а, В, С какие-то выражения от переменной х. Или просто числа.
Теорема: Метод рационализации неравенства с логарифмами:
- Знак выражения $\log_aB-\log_aC$ совпадает со знаком $\frac{B-C}{a-1}$ дробно- рационального. (ОДЗ).
- Неравенства $\log_aB-\log_aC > 0$ и $\frac{B-C}{\left(a-1\right)} > 0$ имеют одинаковые решения. При ОДЗ.
- В неравенстве "произведение < 0" множитель в виде разности логарифмов можно заменить на рациональный аналог:
- Неравенство $X\cdot Y\cdot\left(\log_aB-\log_aC\right)\cdot Z < 0$ эквивалентно $X\cdot Y\cdot\left(\frac{B-C}{\left(a-1\right)}\right)\cdot Z < 0$
Стратегия: вместо логарифмического неравенства иногда удобнее решать его рационализованный аналог - методом интервалов, путем нахождения критических точек обнуления множителей и делителей . Сравнение разности логарифмов с нулем эквивалентно Сравнению дробно-рационального с нулем!
Пример 2: Решить неравенство $\log_{5-x}\left(\frac{1}{9}\right) < 2$
- ОДЗ $5-x>0$ ; $5-x\ne 0$
- Превратим в разность логарифмов $\log_{5-x}\left(\frac{1}{9}\right) < \log_{5-x}\left(5-x\right)^2$ $\log_{5-x}\left(\frac{1}{9}\right)-\log_{5-x}\left(5-x\right)^2 < 0$
- Рационализуем по формулам: $\frac{\left(\frac{1}{9}-\left(5-x\right)^2\right)}{\left(5-x-1\right)} < 0$ . Разложим в скобках на множители
- $\frac{\left(\frac{1}{3}-5+x\right)\left(\frac{1}{3}+5-x\right)}{\left(4-x\right)} < 0$ получим $\frac{\left(x-\frac{14}{3}\right)\left(\frac{16}{3}-x\right)}{\left(4-x\right)} < 0$
- Метод интервалов: критические точки $4 < \frac{14}{3} < 5 < \frac{16}{3}$ - обнуления каждого множителя и ОДЗ
- Контрольные точки $0$; $4,5$; $4,9$; $5,1$; $10$ и проверим и неравенство - знаки и ОДЗ.
- Проверим, например $x = 4,9$. Получим знаки множителей $\frac{\left(+\right)\left(+\right)}{\left(-\right)} < 0$ - выполняется. ОДЗ тоже выполняется.
- $x= 0$ выполняется. $x = 4,5$ выполняется. $x = 4,9$ выполняется. $x= 5,1$ не выполняется. $x= 10$ не выполняется.
- Все проверки привели к решениям, интервалам: ответ $x < 4$ $4 < x < \frac{14}{3}$ $\frac{14}{3} < x < 5$
- Напоминание: "Сокрашенное умножение": разложение разности квадратов $a^2-b^2=\left(a-b\right)\left(a+b\right)$
- "Виета": разложение на множители квадратного $ax^2+bx+c=a\cdot\left(x-x_1\right)\cdot\left(x-x_2\right)$ . По корням.
- "Вынос за скобки": $ax^2-bx=x\cdot\left(ax-b\right)$ $ax+ay=a\cdot\left(x+y\right)$
Пример 3: Решить неравенство $\log_{\frac{1}{4}}\left(3-x\right)\ge\log_{\frac{1}{4}}\left(2x+6\right)$
- ОДЗ $3-x>0$ $2x+6>0$
- Превратим в разность логарифмов $\log_{\frac{1}{4}}\left(3-x\right)-\log_{\frac{1}{4}}\left(2x+6\right)\ge0$
- Рационализуем по формулам: $\frac{\left(3-x\right)-\left(2x+6\right)}{\left(\frac{1}{4}-1\right)}\ge0$ , упростим $\frac{-3\left(x+1\right)}{\left(\frac{1}{4}-1\right)}\ge0$
- Метод интервалов: критические точки $-3 < -1 < 3$ - обнуления каждого множителя и ОДЗ
- Контрольные точки $-10$; $-2$; $0$; $10$ и проверим и неравенство - знаки и ОДЗ.
- Здесь неравенство нестрогое, поэтому надо проверить "концы" интервалов: точка $x=-1$ удовлетворяет.
- В ответы наберем те интервалы, в которых контрольные точки удовлетворяют ответ $-1\le x<3$
Пример 4: Решить неравенство $\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}\left(4-x\right) > -1$
- ОДЗ $x>0$ $4-x>0$ используем $-1=\log_{\frac{1}{3}}3$
- $\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}\left(4-x\right) > \log_{\frac{1}{3}}3$ Нужна разность 2-х log: $\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}\left(4-x\right)-\log_{\frac{1}{3}}3 > 0$
- Объединим последные логарифмы в один: $\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}3\left(4-x\right) > 0$
- Рационализуем $\frac{\left(x-3\left(4-x\right)\right)}{\left(\frac{1}{3}-1\right)} > 0$ , упростим: $\frac{\left(4x-12\right)}{\left(\frac{1}{3}-1\right)} > 0$
- Критические точки в порядке возрастания: $0 < 3 < 4$, ответ $0 < x < 3$
Пример 5: Решить неравенство $\log_{x^2}\left(x-1\right)^2\le1$
- ОДЗ $\left(x-1\right)^2>0$ $x^2>0$ $x^2\ne1$ используем $1=\log_{x^2}\left(x^2\right)$
- метод рационализации наиболее эффективен в уравнениях где в основании логарифма выражение от неизвестного.
- Превратим в разность логарифмов $\log_{x^2}\left(x-1\right)^2\le\log_{x^2}\left(x^2\right)$ $\log_{x^2}\left(x-1\right)^2-\log_{x^2}\left(x^2\right)\le0$
- Рационализуем $\frac{\left(x-1\right)^2-x^2}{\left(x^2-1\right)}\le0$ $\frac{-\left(2x-1\right)}{\left(x-1\right)\left(x+1\right)}\le0$
- Критические точки в порядке возрастания: $-1 < 0 < 1/2 < 1$, Подберем контрольные точки, проверим неравенство и ОДЗ:
- нестрогое, поэтому уточним "концы", ответ $-1 < x < 0$ $0 < x\le\frac{1}{2}$ $x > 1$
Пример 6: Решить неравенство $\log_{0,2}^2x\ge 6+\log_5x$
- ОДЗ $x>0$ используем преобразование $\log_5x=-\log_{0,2}x$
- "подведем" к замене, основание 5 переделаем на основание 0,2: $\log_{0,2}^2x\ge 6-\log_{0,2}x$
- замена $y=\log_{0,2}x$ неравенство подстановки $y^2\ge 6-y$
- $y^2+y-6\ge 0$ корни квадратного выражения $y_1=2$ $y_2=-3$
- Разложим квадратное на множители, Виета, $\left(y-2\right)\left(y+3\right)\ge 0$
- И, не решая неравенство, именно здесь сделаем "возврат" к старому неизвестному
- $\left(\log_{0,2}x-2\right)\left(\log_{0,2}x+3\right)\ge 0$ нам нужны разности логарифмов, ... переделаем
- $\left(\log_{0,2}x-\log_{0,2}0,2^2\right)\left(\log_{0,2}x+\log_{0,2}0,2^3\right)\ge 0$ сумму надо превратить в разность
- $\left(\log_{0,2}x-\log_{0,2}0,2^2\right)\left(\log_{0,2}x-\log_{0,2}0,2^{-3}\right)\ge 0$ Умножение разностей логарифмов "сравнить" с нулем
- Знак умножения должно быть положительным. Но знак каждой скобки-разности такой же как и их "рационального" аналога. Значит ...
- Метод Рационализации: $\frac{x-0,04}{0,2-1}\cdot \frac{x-125}{0,2-1}\ge 0$ $\Leftrightarrow$ $\left(x-0,04\right)\left(x-125\right)\ge 0$
- Метод интервалов: критические точки $0,04$ и $125$ - точки обнуления Еще от ОДЗ точка $0$
- Выберем контрольные точки на всех интервалах разбиения $0<0,04<125$ проверим неравенство и ОДЗ, знаки внутри скобок.
- Проверка контрольных точек $-1$, $\frac{1}{125}$, $5$, $625$ покажет какие интервалы годятся ответ $x\in \left(0;0,04\right]$ $x\in \left[125;+\infty \right)$
Алгоритм: "Метод рационализации логарифмического неравенства".
- шаг 1: Превращаем неравенство к виду "разность логарифмов сравнить с 0":
- . $\log_aB-\log_aC < 0$
- Шаг 2: Разность логарифмов заменим на его рациональный аналог
- . вместо $\log_aB-\log_aC$ исследуем знаки рационального $\frac{B-C}{\left(a-1\right)}$
- Шаг 3: Ищем решения "рационализированного" неравенства методом интервалов
- . $\frac{B-C}{\left(a-1\right)} < 0$
- Шаг 4: Если понадобиться, разложим каждый множитель на простые множители. В контрольных точках анализируем знаки каждого простого множителя, делителя и проверяем: удовлетворяется ли рационализированное неравенство и ОДЗ.
- Дополнение: Если неравентство превратилось в вид (с дополнительными $X$, $Y$, $Z$ ... множителями)
- $X\cdot Y\cdot\left(\log_aB-\log_aC\right)\cdot Z < 0$ то решаем "рационализированный" $\frac{X\cdot Y\cdot\left(B-C\right)\cdot Z}{\left(a-1\right)} < 0$
Замечание: В неравенствах выше важно то, что произведение сравнивается с нулем. Для уравнений это приводило к разбиению на случаи : какой либо множитель должен стать нулем. В неравентствах вида "слева произведение или деление <> справа 0 " нам достаточно знать знаки множителей / делителей чтоб понять - выполняется ли <сравнение> с нулем.
Пример 7: Решить неравенство $3\log^2_{\frac{1}{3}}x+5\log_{\frac{1}{3}}x-2 > 0$
- ОДЗ $x>0$
- замена $y=\log_{\frac{1}{3}}x$ $3y^2+5y-2 > 0$ находим корни: $y_1=\frac{5+\sqrt{49}}{6}=2$ $y_2=-\frac{1}{3}$
- Разложим на множители, Виета, $3\cdot\left(y-2\right)\cdot\left(y+\frac{1}{3}\right) > 0$ и тут же "возврат" $3\cdot\left(\log_{\frac{1}{3}}x-2\right)\cdot\left(\log_{\frac{1}{3}}x+\frac{1}{3}\right) > 0$
- Организуем разности log и рационализируем каждый множитель: $3\cdot\left(\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}\left(\frac{1}{9}\right)\right)\cdot\left(\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}\left(\sqrt[3]{3}\right)\right) > 0$
- Получим "рациональный аналог" $3\cdot\frac{\left(x-\frac{1}{9}\right)\cdot\left(x-\sqrt[3]{3}\right)}{\left(\frac{1}{3}-1\right)\cdot\left(\frac{1}{3}-1\right)} > 0$
- Расставим критические точки, в том числе от ОДЗ: .... подумаем - что за число $\sqrt[3]{3}$ ?
- Интервалы разбиения ... анализ рационального неравенства на контрольных точках и выполняется ли ОДЗ...
- Например, контрольная точка $x=0,5$. Знак всего выражения будет отрицательным. Значит неравенство не удовлетворяется.
- Интервал до 0 не годится, т.к. не проходит ОДЗ. ответ $0 < x < \frac{1}{9}$ , $x > \sqrt[3]{3}$
Пример 8: Решить неравенство $\log_{\sqrt[3]{9x}}\sqrt{\frac{x^3}{3}}+\log_{\sqrt[3]{3x^2}}\sqrt{27x}\le3$
- О.Д.З. $x>0$ $\sqrt[3]{9x}\ne 1$ $\sqrt[3]{3x^2}\ne 1$
- Степени под логарифмом лучше, чем корни. $\log_{\left(9x\right)^{\frac{1}{3}}}\left(\frac{x^3}{3}\right)^{\frac{1}{2}}+\log_{\left(3x^2\right)^{\frac{1}{3}}}\left(27x\right)^{\frac{1}{2}}\le3$ Чем? Чем корни!. Дробная степень.
- С аргумента показатель степени "спускается" множителем, с основания "делителем": $\frac{3}{2}\log_{9x}\left(\frac{x^3}{3}\right)+\frac{3}{2}\log_{3x^2}\left(27x\right)\le3$
- $\log_{9x}\left(\frac{x^3}{3}\right)+\log_{3x^2}\left(27x\right)\le2$ Перейдем к основанию $3$ , будет проще: $\frac{\log_3\frac{x^3}{3}}{\log_39x}+\frac{\log_327x}{\log_33x^2}\le2$
- $\frac{\log _3x^3-\log _33}{\log _39+\log _3x}+\frac{\log _327+\log _3x}{\log _33+\log _3x^2}\le 2$, Упростим $\frac{3\log _3x-1}{2+\log _3x}+\frac{3+\log _3x}{1+2\log _3x}\le 2$ и увидим замену ....
- замена $y=\log _3x$ $\frac{3y-1}{2+y}+\frac{3+y}{1+2y}\le 2$
- Упростим числитель: $\frac{6y^2+y-1+y^2+5y+6-4y^2-10y-4}{\left(2+y\right)\left(1+2y\right)}\le 0$ $\Leftrightarrow$ $\frac{3y^2-4y+1}{\left(2+y\right)\left(1+2y\right)}\le 0$
- Разложим на множители, Виета, $\frac{3\left(y-1\right)\left(y-\frac{1}{3}\right)}{\left(2+y\right)\left(1+2y\right)}\le 0$ ... сравнение с нулем удобнее с множителями.
- $\frac{3\left(y-1\right)\left(y-\frac{1}{3}\right)}{2\left(y+2\right)\left(y+\frac{1}{2}\right)}\le 0$ Вот здесь и совершим возврат от $y$ к $x$ $\frac{3\left(\log _3x-1\right)\left(\log _3x-\frac{1}{3}\right)}{2\left(\log _3x+2\right)\left(\log _3x+\frac{1}{2}\right)}\le 0$
- Для метода рационализации нужны разности логарифмов. Как? сумма в разность: $\log_3a+\log_3b=\log_3a-\log_3\left(\frac{1}{b}\right)$
- $\frac{3\left(\log _3x-\log _33\right)\left(\log _3x-\log _33^{\frac{1}{3}}\right)}{2\left(\log _3x-\log _3\frac{1}{9}\right)\left(\log _3x-\log _33^{-\frac{1}{2}}\right)}\le 0$ В каждом множителе $\log_aB-\log_aC$ заменим на рациональный аналог $\frac{B-C}{\left(a-1\right)}$
- $\frac{3\cdot \frac{x-3}{3-1}\cdot \frac{x-3^{\frac{1}{3}}}{3-1}}{2\cdot \frac{x-\frac{1}{9}}{3-1}\cdot \frac{x-3^{-\frac{1}{2}}}{3-1}}\le 0$ Упростим дробно-рациональное неравенство $\frac{\left(x-3\right)\cdot \left(x-3^{\frac{1}{3}}\right)}{\left(x-\frac{1}{9}\right)\cdot \left(x-3^{-\frac{1}{2}}\right)}\le 0$
- Неравенство, состоящее из множителей и сравнения с нулем ... решаем методом интервалов.
- Критические точки по возрастанию, включая $x=0$ от ОДЗ: $0<\frac{1}{9}<\frac{1}{\sqrt{3}}<3^{\frac{1}{3}}<3$
- На полученных интервалах выберем контрольные точки ... отследим знаки каждой скобки ... проверим сравнение с нулем:
- Получим: неравенство и ОДЗ выполняется в двух интервалах ответ $\frac{1}{9}<x<\frac{1}{\sqrt{3}}$ $3^{\frac{1}{3}}\le x\le 3$
Неравенства из ЕГЭ восток 2023


В пустых ЛИСТах #71 - #75 интерактивно можно решать любые неравенства, шаги его решений, хоть из сайта сдам.егэ:
Неравенства из Задания №14, ЕГЭ - профиль