I. Тестирование по задачам ЕГЭ №5, вероятность, сложная
Порешайте комбинированные задачи по темам ЕГЭ №5. Если обнаружились проблемы, то повторите основы теории вероятности.
II. Теория: определения, свойства, формулы.
Ознакомьтесь с кратким изложением основных свойств, формул теории вероятности.
III - IV . Примеры решений. Упражнения для закрепления
Тренируйтесь по типам задач, проверяйте и уточняйте свои знания и навыки решения типовых задач
Рекоммендуемые интерактивные уроки mathematicos по темам теории вероятности
О главном по теме типовые задачи по теме "вероятность, по-сложнее"
Равновероятные события: Множество, в котором каждое одиночное-конкретное-элементарное имеет одинаковый шанс случится .
Вероятность события $A$ равна отношению числа случаев $m$, благоприятствующих ему, к числу $n$ - общего числа $n$ равновероятных.
$P(A)=\frac{m}{n}$, $m$ - благоприятных к $A$, $n$ единственно возможных, всех равновозможных, несовместных случаев.
Вероятность геометрический ... попадания точки внутрь части: отношение ее размера к размеру всей области.
- Правило "Умножение вероятностей И,И ": Вероятность события "и то, и то случается" равно произведению отдельных.
- Правило "Сложение вероятностей ЛИБО,ЛИБО ": Вероятность суммы несовместных событий равна сумме вероятностей.
- Вероятность появления достоверного $P(A)=1$, Вероятность появления невозможного события $P(A)=0$
- Вероятность противоположного события $P(\overline{A})=1-P(A)$ . Вероятность событий полной группы, равна единице.
- Вероятность наступления события = количество благопрятных : количество всевозможных равновероятных .
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий. Сумма $S$ событий $A,B,C,\ldots,N$ обозначается так: $S=A+B+C+\ldots+N$.
Произведением, или пересечением, событий называется событие, состоящее в совместном появлении всех этих событий. Произведение $S$ событий $A,B,C,\ldots,N$ обозначается $S=ABC\ldots{N}$.
Вероятность статистический ... число, около которого группируются частоты этого события по мере увеличения числа испытаний.
Вероятность геометрический ... попадания точки внутрь части: отношение ее размера к размеру всей области.
Бинарные исходы -- "Да"/"Нет" , "Попал"/"Не попал" : Вероятность того, что при ${n+k}$ выстрелах случилось: в любом порядке ровно $n$ исходов "да"-($p$) и ровно $k$ исходов "нет"-($1-p$) равна биномиальному $C_{n+k}^k\cdot p^n\cdot (1-p)^k$
Условная вероятность: $p\left(B|A\right)=\frac{p\left(AB\right)}{p\left(A\right)}$ события $B$ при условии гаратнированного наступления $A$ ==== вероятность того, что случится событие $B$ при том, что событие $A$ точно наступает.
Формула условной вероятности: $p\left(AB\right) = p\left(A\right) \cdot p\left(B|A\right)$ ... случатся оба: и $A$, и $B$
Формула объединения vs пересечение: $p\left(A+B\right) = p\left(A\right)+p\left(B\right) - p\left(AB\right)$ ... случится хотя бы одно: или $A$, или $B$
I. Тестирование: ЕГЭ задания №5, Вероятность, по-сложнее:
II. Основы теории вероятностей
- Событием - любой факт, любой исход, который может произойти в результате данного опыта или испытания.
- Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
- События называются совместными, если наступление одного из них не исключает наступления другого.
- В противном случае события называются несовместными.
- Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта: вероятность = 1.
- Событие называется невозможным, если оно не может произойти в условиях данного опыта: вероятность = 0.
- Событие возможное, или случайное, если в результате опыта оно может появиться, но может и не появиться.
- Равновероятные событие, - ни одно из них не имеет преймущества "случиться" по сравнению с другими: ни чаще, ни реже ...
- Несколько событий в образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них.
- Противоположное событие $\overline{A}$ : которое обязательно должно произойти, если не наступило некоторое событие $A$.
Операции над событиями: понятие суммы и произведения событий.
- Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
- Сумма $S$ событий $A,B,C,\ldots,N$ обозначается так: $S=A+B+C+\ldots+N$.
- Если $A$ - "попадание в цель при 1-ом выстреле", $B$ — "при 2-ом," то событие $C=A+B$ есть попадание в цель вообще,
- .... безразлично, при каком выстреле — первом, втором или при обоих вместе: " либо $A$, либо $B$, либо ОБА "
- Произведением, или пересечением, событий называется событие, состоящее в совместном появлении всех этих событий.
- Произведение $S$ событий $A,B,C,\ldots,N$ обозначается $S=ABC\ldots{N}$.
- Если $A$ - "попадание в цель при 1-ом выстреле", $B$ — "при 2-ом,", то событие $C=A\cdot B$ "в цель попали при обоих выстрелах".
Классическое определение вероятности случайного события
- Количественное сравнение событий по степени возможности ... называется вероятностью события.
- Вероятностью события называется число, являющееся выражением меры объективной возможности, шанса появления события.
- Вероятность возможного наступления события $A$ будем обозначать символом $P(A)$.
- классическое определение вероятности: Вероятность события $A$ равна отношению числа случаев $m$, благоприятствующих ему, к числу $n$ - общего числа $n$ равновероятных.
- $P(A)=\frac{m}{n}$, $m$ - благоприятных, $n$ единственно возможных, всех равновозможных, несовместных случаев.
Свойства вероятности: $0\leqslant{m}\leqslant{n}$, $~0\leqslant{P(A)}\leqslant1$
- Вероятность "случится $A$" - какую долю составляет благоприятствующее число случаев от общего числа случаев:
- Если все случаи являются благоприятствующими данному событию $A$, то это событие обязательно произойдет. Достоверное!
- Вероятность появления достоверного события $P(A)=1$, так как в этом случае $m=n$: $P(A)=\frac{m}{n}=1$.
- Если нет ни одного случая, благоприятствующего данному событию $A$, то это событие произойти не может. Невозможно!
- Вероятность появления невозможного события $P(A)=0$, так как в этом случае $m=0$: $P{A}=\frac{0}{n}=0$.
- Вероятность наступления событий, образующих полную группу, равна единице. "что-то произойдет!"
- Вероятность наступления противоположного события $\overline{A}$ определяется так же, как и вероятность не-наступления события $A$:
- $P(\overline{A})=\frac{n-m}{n}=1-\frac{m}{n}$ где $(n-m)$ — число случаев, благоприятствующих появлению противоположного события $\overline{A}$ .
- Вероятность противоположного события $\overline{A}$ равна $P(\overline{A})=1-P(A)$, разнице $1$ и вероятностью $A$:
- Достойнство теории:, вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
Вероятность статистический ... число, около которого группируются частоты этого события по мере увеличения числа испытаний.
Вероятность геометрический ... попадания точки внутрь части: отношение ее размера к размеру всей области.
Аксиомы теории вероятностей: $0\leqslant{m}\leqslant{n}$, $~0\leqslant{P(A)}\leqslant1$
- Аксиома 1. Каждому событию $A$ соответствует ее вероятность - число $P(A)$, с ограничением $0\leqslant{P(A)}\leqslant1$
- Аксиома 2. Вероятность достоверного события равна единице.
- Аксиома 3. Вероятность невозможного события равна нулю.
- Аксиома 4. (аксиома сложения). Вероятность суммы двух несовместных событий равна сумме их вероятностей.

III. Примеры решений сложных задач теории вероятностей
Задача 1, "Два уровня выбора": На первом уровне с указанными вероятностями выбирается либо событие $A$ либо событие $B$. Затем, на втором уровне выбора, из события $A$ может получиться одно из трех $M$, $N$, $K$; а из события $B$ одно из $N$, $K$, $L$.
- Произведение событий $AN$ ( наступает "и $A$ и $N$" ): $P(AN)=0,3\cdot 0,4=0,12$ - умножение вероятностей.
- Правило "Умножение вероятностей И,И ": Вероятность события "и то, и то случается" равно произведению отдельных.
- Еще Произведения: $P(AM)=0,3\cdot 0,5=0,15$ $P(BN)=0,7\cdot 0,3=0,21$ $P(BK)=0,7\cdot 0,25=0,175$
- Полная группа событий $A+B$ : либо $A$ случится, либо $B$ . $P(A+B)=1$
- Еще полные группы: $M+N+K$ - либо $M$, либо $N$, либо $K$. $P(M+N+K)=1$. Аналогично, $P(N+K+L)=1$
- Вопрос: Какова вероятность того, что случится событие $N$ ?
- $N$ может случится по двум путям: либо сперва $A$, затем $N$; либо сперва $B$, затем $N$. "Две пути либо $AN$, либо $BN$.
- Событие $N$ является суммой двух событий $N=AN+BN$. Но они несовместные, взаимоисключающиеся ...
- Правило "Сложение вероятностей ЛИБО,ЛИБО ": Вероятность суммы несовместных событий равна сумме вероятностей.
- Вероятность наступления события $N$ равна $P(N)=P(AN+BN)=P(AN)+P(BN)=0,3\cdot 0,4+0,7\cdot 0,3=0,33$.
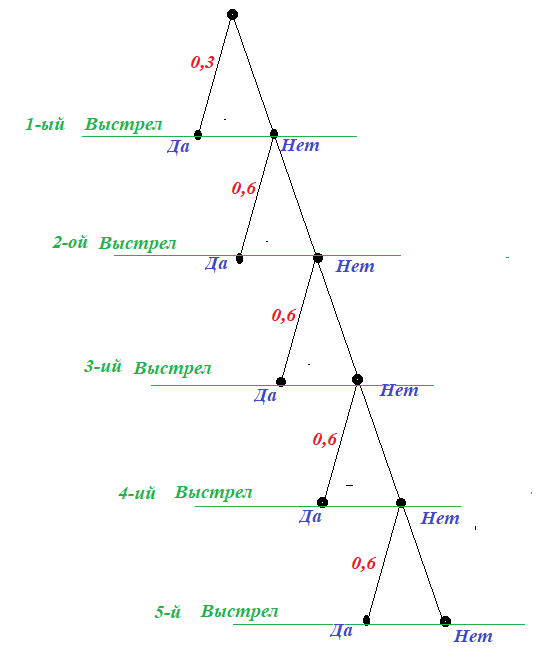
Задача 2: [ege.sdamgia.ru №320187] При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна $0,3$, а при каждом последующем — $0,6$. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
- Дано: $a=0,3$ - попадание при 1-ом выстреле, $b=0,6$ - попадание при следующих одиночных выстрелах.
- Найдем вероятности: $p_1$ - цель будет поражена с первого раза, $p_2$ - со второго раза, $p_3$ - с третьего раза, и т.д.
- Найдем вероятности: $q_1$ - цель не будет поражена с первого раза, $q_2$ - нет со второго раза, $q_3$ - нет с третьего раза, и т.д.
- Схема выстрелов: Вероятность поражения цели на следующем шаге = вероятность быть целым на предыдущем умножить на вероятность попадания данного выстрела. Вероятность уцелеть на следующем шаге = вероятность быть целым на предыдущем умножить на промах текущего выстрела.
- После первого выстрела: вероятность поражения $p_1=a=0,3$ , вероятность промаха $q_1=1-a=1-0,3=0,7$.
- После 2-го выстрела: (поражена) = (промах 1-го) * (попадание при 2-ом) ... $p_2=q_1\cdot b=(1-a)\cdot b=0,42$. Цель не поражена $q_2=q_1\cdot (1-b)=(1-a)\cdot (1-b)=0,28$
- После 3-го выстрела: (поражена) = (промах после 2-го) * (попадание при 3-ем) ... $p_3=q_2\cdot b=(1-a)\cdot (1-b)\cdot b=0,168$. Цель не поражена $q_3=q_2\cdot (1-b)=(1-a)\cdot (1-b)\cdot (1-b)=0,112$
- После 4-го выстрела: (поражена) = (промах после 3-го) * (попадание при 4-ом) ... $p_4=q_3\cdot b=(1-a)\cdot (1-b)\cdot (1-b)\cdot b=0,0672$. Цель не поражена $q_4=q_3\cdot (1-b)=(1-a)\cdot (1-b)\cdot (1-b)\cdot (1-b)=0,0448$
- После 5-го выстрела: (поражена) = (промах после 4-го) * (попадание при 5-ом) ... $p_5=q_4\cdot b=(1-a)\cdot (1-b)\cdot (1-b)\cdot (1-b)\cdot b=0,02688$. Цель не поражена $q_5=q_4\cdot (1-b)=(1-a)\cdot (1-b)\cdot (1-b)\cdot (1-b)\cdot (1-b)=0,01792$
- Получилось: после 5-го выстрела вероятность уцелеть равна $1-0,01792>0,98$. Значит, достаточно $5$ выстрелов.
- Ответ: При $5$ выстрелах вероятность поражения цели выше $0,98$
- Умножения Вероятностей: Если последовательные события один за другим, ветви ... Вероятности перемножаются.
- Правило ветвей: Вероятность "реализовалась данная ветвь процесса" = умножение вероятностей его шагов, "ребер".
- Замечание 1: Вероятность поражения на $n$-ом выстреле $p_n=(1-a)\cdot (1-b)^{n-2}\cdot b$
- Замечание 2: Вероятность уцелеть после $n$ - го выстрела $q_n=(1-a)\cdot (1-b)^{n-1}$
- Вероятность уцелеть после $5$ - го $1-q_5$. Вероятность не уцелеть за $5$ выстрелов $p_1+p_2+p_3+p_4+p_5$.
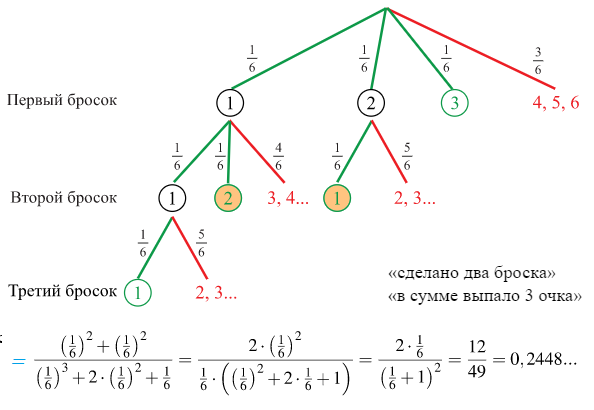
Задача 3: Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна $3$. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
- Решение: Изобразим с помощью дерева возможные исходы.
- Зелёным цветом отмечены исходы, удовлетворяющие условию «сумма выпавших очков равна $3$».
- Оранжевым исходы, удовлетворяющие условию «сумма очков, выпавших ровно за два броска равна $3$».
- Тогда вероятность события «сделано два броска» при условии «в сумме выпало $3$ очка» равна: $=0,2448$... Ответ: $0,24$
Задача 4:: 48% мужчин, 12.5% пенсионеров ....
Задача 5:: Для поступление в институт нужны баллы ....
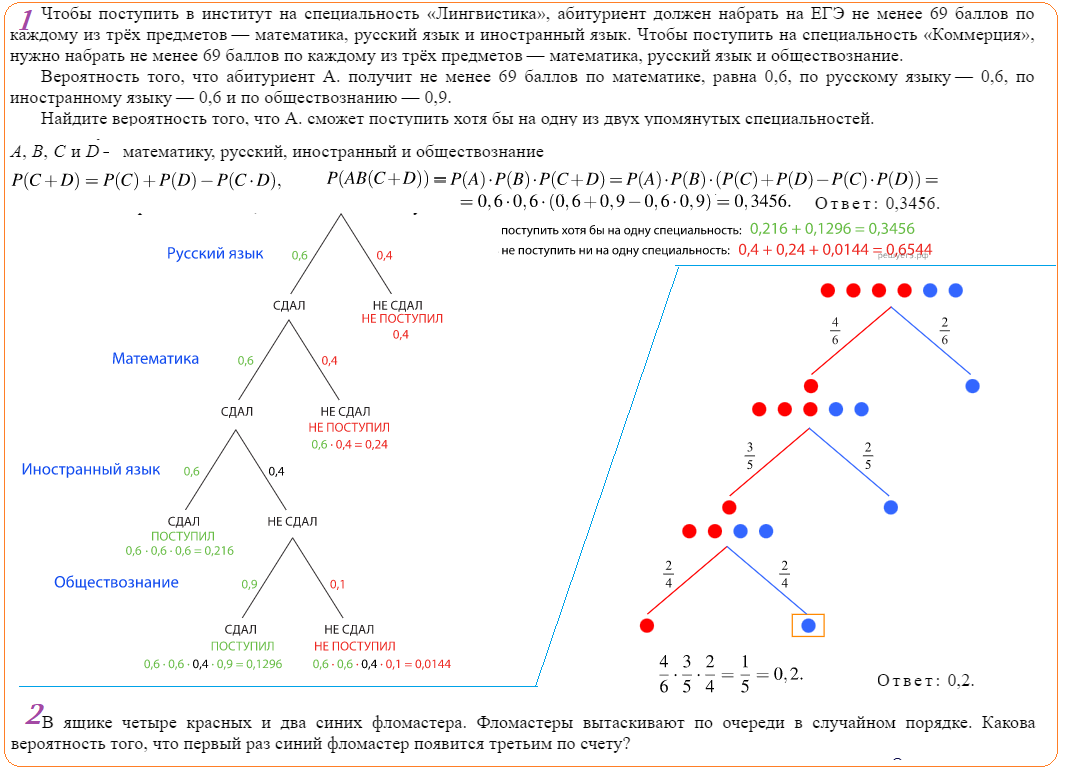
Задача 6:: Фломастеры: 3 красных, 2 синих ....
Задача 7:: ПЦР-тест подтвеждает 86% случаев ...

Подробнее на эти темы, смотрите теорию:
Вероятности бинарных процессов: "промах - попадание".
Задача 8: Стрелок попадает в цель с вероятностью 0,6. Какова вероятность того, что при пяти выстрелах стрелок попадет ровно 3 раза.
- Решение: Вероятность "попадания" $p=0,6$ Вероятность "промаха" противоположное $q=1-p=0,4$ .
- "попадание" и "промах" суть противоположные события. Сумма вероятностей $p+q=1$ - полнота вероятности!
- $(p+q)^5=1$ Бином Ньютона для степени 5: $(p+q)^5=p^5+5\cdot p^4q+10\cdot p^3q^2+10\cdot p^2q^3+5\cdot pq^4+q^5$
- каждое отдельное слагаемое Бинома равно вероятности попадания в цель в точности столько раз, в какой степени $p$ входит в это слагаемое!
- зряче: $1$ = [$p^5$] + [$5\cdot p^4q$] + [$10\cdot p^3q^2$] + [$10\cdot p^2q^3$] + [$5\cdot pq^4$] + [$q^5$]
- "что-то случится" = "все 5 попал" + "попал 4 раза" + "попал 3 раза" + "попал 2 раза" + "только 1 раз" + "все промахи"
- Вероятность ( из пяти исходов 3 будут удачными ) = $10\cdot p^3q^2$ = $C_5^3\cdot p^3q^2$ . Число Сочетаний: $C_5^3=\frac{5\cdot 4\cdot 3}{1\cdot 2\cdot 3}=10$.
-
Ответ: $10\cdot p^3(1-p)^2=10\cdot 0,6^3\cdot 0,4^2=10\cdot 0,216\cdot 0,16=0,3456$
-
Решим эту же задачу прямым нахождением вероятности Схематически: 0 = промах, 1 - попадание.
- Вариант одного из возможных благоприятных событий (0, 1, 1, 0, 1) - три раза попал именно в 2-ой, 3-ей и 5-ой попытке.
- Какова вероятность ровно такого события: попытки идут друг - за другом, последовательно и независимо друг от друга. :}
- По Правилу Умножения Вероятностей Независимых $p_{01101}=q\cdot p\cdot p\cdot q\cdot p=p^3q^2=p^3\left(1-p\right)^2$
- Но {01101} лишь один вариант расположения трех единиц в пяти местах. Другие варианты ... {01110}, {10110} ...
- Все эти варианты-события содержат ровно три единицы, а потому их вероятности одинаковые $p^3\left(1-p\right)^2$. Но сколько их?
- Вариантов выбора трех мест из пяти - Число Сочетаний: $C_5^3=10$: В пятерке надо выбрать тройку без учета порядка.
- Разные варианты ..{01101}... {01110} ... {10110} .. не совместны друг с другом: либо одно, либо другое ... или - или
- По Правилу Сложения Несовместных наша вероятность 3 из 5 = [$10$ вариантов] * [$p^3\left(1-p\right)^2$],
О вероятностях в Бинарных исходах: однократное событие с исходами "да" или "нет"
Теорема: Если "да" выпадает с вероятностью $p$, то при $n+k$ попытках:
- вероятность наступления в конкретном порядке ровно $n$ исходов "да" и $k$ исходов "нет" равна $ p^n\cdot (1-p)^k$
- вероятность наступления в любом порядке ровно $n$ исходов "да" и $k$ исходов "нет" равна $C_{n+k}^k\cdot p^n\cdot (1-p)^k$
Задача 9: Монета подбрасывается 9 раз. Найти вероятность выпадения "орла" менее 4 раз.
- Бинарные исходы "орел", "решка" с одинаковыми вероятностями успеха - не успеха: $p=\frac{1}{2}$ $q=0,5$
- 9 попыток, Бином Ньютона 9-ой степени : $(p+q)^9=p^9+C_9^8\cdot p^8q+C_9^7\cdot p^7q^2+....+C_9^1\cdot pq^8+q^9$
- Менее 4 раз: значит либо 3, либо 2, либо 1, либо 0. Их вероятности представлены последними 4 слагаемыми в Биноме
- Сложение Несовместных Вероятность ( менее 4 раз ) $a$ = $C_9^3\cdot p^3q^6+C_9^2\cdot p^2q^7+C_9^1\cdot pq^8+q^9$
- Расчеты: $C_9^3=\frac{9\cdot 8\cdot 7}{1\cdot 2\cdot 3}=84$ $C_9^2=\frac{9\cdot 8}{1\cdot 2}=36$ $C_9^1=9$ $p^3q^6=p^2q^7=p^1q^8=q^9=0,5^9$
- Ответ: вероятность менее 4 "орла" $a=(84+36+9+1)\cdot 0,5^9=\frac{120}{512}=\frac{15}{64}$
Задача 10: На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу $C$.
- Решение. На пути к выходу $С$ паук встретит $4$ развилки. На каждой из них он с вероятностью $0,5$ может выбрать или путь, ведущий к выходу $С$, или другой путь. Это независимые события, вероятность их произведения (события, состоящего в том, что паук дойдет до выхода $С$) равна произведению вероятностей этих событий.
- Поэтому вероятность прийти к выходу С равна $(0,5)^4 = 0,0625$. Ответ: $0,0625$.

- Правило I "Сложения": вероятность непересекающихся $p\left(X+Y\right)=p\left(X\right)+p\left(Y\right)p(X+Y)=p(X)+p(Y)$ равна сумме.
- ( например, $p\left(M+N\right)=p\left(M\right)+p\left(N\right)=\frac{7}{16}=\frac{1}{4}+\frac{3}{8}p(M+N)=p(M)+p(N)=$
- ранее вычислялось. (события или из $M$ или из $N$)
- пример трех непересекающихся: $p\left(M+C+N\right)=p\left(M\right)+p\left(C\right)+p\left(N\right)p(M+C+N)=p(M)+p(C)+p(N)$
- Правило II "Сложения ---": вероятность объединения пересекающихся $p\left(A+B\right)=p\left(A\right)+p\left(B\right)-p\left(C\right)p(A+B)=p(A)+p(B)−p(C)$ ( минус $С$ - пересечение множеств $A$ и $B$ )
Что такое Условная вероятность события $B$ при условии $A$ ?
- Какова вероятность, что случится событие $B$ при том, что событие $A$ точно наступает.
- Если случиться что-то из (эЛс) элементарных событий из $A$, то какова вероятность, что это эЛс будет из $B$.
- Грубо говоря: сколько среди всех эЛс из $A$ доля эЛс-ов из $B$.
- Формула условной вероятности: $p\left(B|A\right)=\frac{p\left(AB\right)}{p\left(A\right)}$
- здесь $p\left(AB\right)$ вероятность пересечения, $AB$ означает, что его каждое эЛс одновременно входит и в $A$ и в $B$.
- Осмысление: условная вероятность = "благоприятние" (и в $A$ и в $B$) деленное на "всевозможные" из $A$.
- Обозначения: $AB$ - пересечение: и $A$ и $B$. $A+B$ - объединение событий: или $A$ или $B$
Формула условной вероятности: $p\left(AB\right) = p\left(A\right) \cdot p\left(B|A\right)$
Формула объединения vs пересечение: $p\left(A+B\right) = p\left(A\right)+p\left(B\right) - p\left(AB\right)$
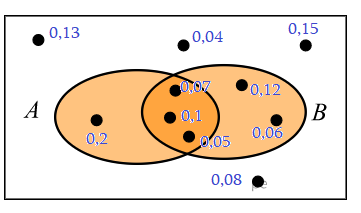
Задача 11: На диаграмме Эйлера показаны события A и B в некотором случайном эксперименте, в котором 10 элементарных событий с указанными вероятностями. Элементарные события показаны точками. Найдите p(B|A) - условную вероятность события B при условии A.
- Событие $A$ состоит из четырех эЛс -или-или....сложение: ${p\left(A\right)}=0,2+0,07+0,1+0,05=0,42$
- Событие $B$ состоит из пяти эЛс -или-или....сложение: ${p\left(B\right)}=0,07+0,1+0,05+0,12+0,06=0,4$
- пересечение $AB$, одновременно и $A$ и $B$ состоит из трех эЛс: ${p\left(AB\right)}=0,07+0,1+0,05=0,22$
- Условное "что-то из $B$ среди эЛс-ов из $A$" $p\left(B|A\right)=\frac{p\left(AB\right)}{p\left(A\right)}=\frac{0,22}{0,42}$
- По другому, доля пересечения внутри $A$: $\frac{p\left(AB\right)}{p\left(A\right)}=\frac{0,07+0,1+0,05}{0,2+0,07+0,1+0,05}=\frac{11}{21}$
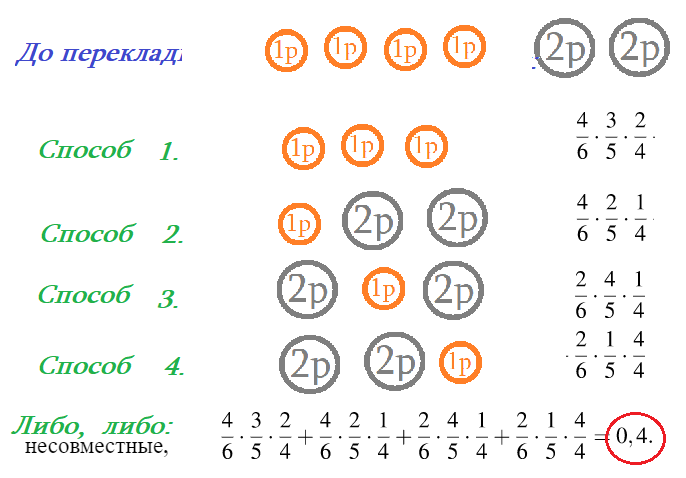
Задача 12: В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
- Петя переложил в другой карман три из четырех рублевых монет и, тогда в 1-м остались две двух-рублевые.
- Или же, переложил две двух-рублевые. Это возможно тремя способами: 1, 2, 2; или 2, 1, 2; или 2, 2, 1.
- Все эти четыре способа несовместны, -либо -либо. Значит правило сложения вероятностей каждого.
- Внутри каждого способа ...и ... и: Например, 2, 1, 2 означает: и 2, и затем 1, и затем 2. Правило умножения!
Задача 13: Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
- Событие $C$ : "пациент болен гепатитом"; Событие $D$ : "пациент не болен гепатитом";
- Событие $A$ : "анализ пациента положителен"; Событие $B$ : "анализ пациента отрицателен";
- Вероятности: $p\left(C\right)=0,05$ $p\left(D\right)=1-p\left(C\right)=0,95$
- анализ дает положительный при условии, что пациент больной (верно) ... условное событие $p\left(A|C\right)=0,9$
- анализ дает отрицательный при условии, что пациент здоров (якобы болен, ложно) ... условное $p\left(B|D\right)=0,01$
- Анализ пациента может быть положительным по двум причинам: или как верный, или как ложный! ...ЛИБО....ЛИБО...
- пациент болеет гепатитом, его анализ верен; пересечение $CA$:, и есть гепатит, и анализ подтвердил, ...И...И... $p\left(CA\right)$
- пациент не болеет гепатитом, его анализ ложен. пересечение $DB$, и нет гепатита, и анализ ошибочен, ...И...И... $p\left(DB\right)$
- Формула Условной Вероятности для $CA$: $p\left(CA\right)=p\left(C\right) \cdot p\left(C|A\right)=0,9 \cdot 0,05 = 0,045$
- Формула Условной Вероятности для $DB$: $p\left(DB\right)=p\left(D\right) \cdot p\left(D|B\right)=0,01 \cdot 0,95 = 0,0095$
- Анализ пациента положительный, (-или - или, Правило сложения) $p\left(CA\right)+p\left(DB\right)=0,045+ 0,0095=0,0545$ Ответ: $0,0545$.
Другое решение, "Очевидное, На Пальцах":: Пусть $10 000$ пациентов. Проследим усредненные ожидания...
- Действительно больны $5$ % $\Rightarrow$ в среднем $500$ больных, $9 500$ здоровых.
- У больных анализ дает положительный результат с вероятностью $0,9$ $\Rightarrow$ $450$ получат положительный, а $50$ отрицательный.
- У здоровых анализ даст ложный положительный с вероятностью $0,01$ $\Rightarrow$ $95$ получат ложно положительный.
- В итоге получили положительный: $450 + 95 = 545$. Благоприятные!. Какая доля среди всех ? $\frac {545}{10000}=0,0545$
Задача 14: В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна $0,3$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,12$. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
- Событие $A$ = кофе закончится в первом автомате, Событие $B$ = кофе закончится во втором автомате.
- Тогда: $A·B$ = кофе закончится в обоих автоматах, $A + B$ = кофе закончится хотя бы в одном автомате.
- По условию $P(A) = P(B) = 0,3$; $P(A·B) = 0,12$.
- Вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
- $P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48$.
- Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна $1 − 0,48 = 0,52$. Ответ: $0,52$.
Другое решение:: Вероятность того, что кофе останется хотя бы в одном автомате равна $1 − 0,12 = 0,88$
- Вероятность того, что кофе останется в первом автомате, равна $1 − 0,3 = 0,7$.
- Вероятность того, что кофе останется во втором автомате, равна $1 − 0,3 = 0,7$.
- $P(A + B) = P(A) + P(B) − P(A·B)$, $0,88 = 0,7 + 0,7 − х$, искомая вероятность $х = 0,52$.
- Замечание: события $A$ и $B$ не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий: $P(A·B) = 0,3·0,3 = 0,09$, однако, по условию, эта вероятность равна $0,12$.
Еще одно решение, "Очевидное, На Пальцах":: Пусть $1000$ дней следили, вели записи ... Проследим усредненные ожидания...
- В первом автомате $300$ раз кончилось кофе, $700$ раз осталось. На втором такая же статистика.
- Но $120$ дней было таких, что в обоих автоматах кончилось кофе.
- Значит, из $1000$ дней "расклад" такой: в обоих кончилось = $120$ дней; кончилось только в первом $300-120=180$ дней; кончилось только во втором также $300-120=180$ дней;
- Вывод: хоть где-то кончилось $120+180+180=480$. еще вывод: нигде не кончилось $1000-480=520$ дней.
- Доля дней, при которых кофе осталось в обоих автоматах благоприятные : все Ответ: $\frac {520}{1000}=0,52$
Задача 15: Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень даётся не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно три мишени» больше вероятности события «стрелок поразит ровно две мишени»?
- Вероятность попадания отдельным выстрелом $0,6$ Вероятность промаха, противоположное $1-0,6=0,4$
- Вероятность попасть в мишень с первого или второго выстрела: $p=0,6+0,4\cdot 0,6=0,84$.
- Вероятность противоположного события стрелок не попадёт в мишень с двух выстрелов, равна $q=1 − 0,84 = 0,16$.
- Для нахождения вероятности события стрелок поразит ровно три мишени или ... две мишени, формулы:
- Бином 3 из 5: $p_5\left(3\right)=C_5^3p^3q^2=\frac{5\cdot4\cdot3}{1\cdot2\cdot3}\cdot0,84^3\cdot0,16^2=10\cdot0,84^3\cdot0,16^2$
- Бином 2 из 5: $p_5\left(2\right)=C_5^2p^2q^3=\frac{5\cdot4}{1\cdot2}\cdot0,84^2\cdot0,16^3=10\cdot0,84^2\cdot0,16^3$
- Искомое отношение вероятностей: $\frac{p_5\left(3\right)}{p_5\left(2\right)}=\frac{0,84^3\cdot0,16^2}{0,84^2\cdot0,16^3}=\frac{0,84}{0,16}=5,25$ Ответ: $5,25$.
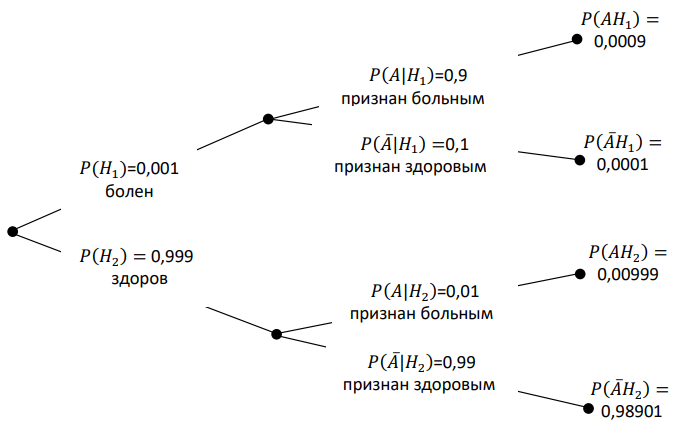
Задача 16: При массовом рентгеновском обследовании населения вероятность обнаружить заболевание туберкулезом у больного туберкулезом равна 0,9, вероятность принять здорового человека за больного равна 0,01. Доля больных туберкулезом по отношению ко всему населению равна 0,001. Найти вероятность того, что человек здоров, если при обследовании он был признан больным.
- Введем события: пациент болен –𝐻1, пациент здоров –𝐻2. Вероятность того, что на обследование поступил больной пациент 𝑃(𝐻1), здоровый - 𝑃(𝐻2).
- Пусть событие А - «пациент признан больным». Тогда событие 𝐴̅– пациент признан здоровым. Сформулируем условные вероятности.
- По результатам обследования признанный больным пациент действительно оказался больным 𝑃(𝐴|𝐻1), признанный здоровым оказался больным 𝑃(𝐴̅|𝐻1), признанный больным на самом деле здоров 𝑃(𝐴|𝐻2), признанный здоровым действительно здоров 𝑃(𝐴̅|𝐻2).
- Соответствующее дерево вероятностей представлено на рис. 2.5.
- Вычислим сначала полную вероятность признания пациента больным 𝑃(𝐴) = 𝑃(𝐻1)𝑃(𝐴|𝐻1) +𝑃(𝐻2)𝑃(𝐴|𝐻2) = 0,001 · 0,9 +0,999 · 0,01 = 0,01089.
- Теперь вероятность того, что здорового пациента при обследовании признали больным, равна 𝑃(𝐻2|𝐴)=𝑃(𝐴|𝐻2)𝑃(𝐴)·𝑃(𝐻2)=(0,01/0,01089)·0,999 ≈ 0,917
- Таким образом, 91,7 % людей, у которых обследование показало результат «болен», на самом деле здоровые люди. Удивительный результат возникает по причине значительной разницы в долях больных туберкулёзом и здоровых. При возникновении такого результата следует сделать повторное обследование.
IV. Упражнения: задачи теории вероятности