I. Тестирование по задачам ЕГЭ №6
Порешайте комбинированные задачи по темам ЕГЭ №6. Если обнаружились проблемы, то повторите теорию решения уравнений.
II - IX. Теория, разбор задач по темам.
Ознакомьтесь с кратким изложением основных методов, преобразований, применяемых при решении уравнений, повторите алгоритмы решений.
X. Упражнения для закрепления
Тренируйтесь по типам задач, проверяйте свои знания и навыки решения типовых уравнений
Рекоммендуемые интерактивные уроки mathematicos по темам решения уравнений
Уравнением называется равенство двух частей, содержащее неизвестную букву, значение которой надо найти. Значение буквы, которое выравнивает обе части , называют корнем или решением уравнения.
Что значит решить уравнение? Это значит найти число, которое при подстановке вместо буквы уравняет обе части, т.е. превратит уравнение в верное числовое равенство. Все, что надо сделать с уравнением - найти его корень. Т.е. то что его уравняет - сравняет - превратит в верное = !
Aлгоритмы решения уравнений: шаг за шагом от исходного уравнения .... I. переходим к равносильному (с тем же корнем), доходим до конечного вида "неизвестное = число"; II. корни уравнения не меняются, если перенести любое слагаемое из одной части в другую с противоположным знаком. III. корни уравнения не меняются, если обе части умножить или разделить на одно и то же отличное от нуля число.
Примеры эквивалентных шагов - преобразований уравнений, равенств:
$A+B=C$ $\Leftrightarrow$ $A=C-B$ ; $A-2x^2+7=B+5x-m$ $\Leftrightarrow$ $A+7-5x+m=B+2x^2$ ; перенос слагаемых
$m\cdot A=B$ $\Leftrightarrow$ $A=\frac{B}{m}$ ; $-\frac{3}{7} \cdot A=22$ $\Leftrightarrow$ $A=\frac{22}{-\frac{3}{7}}$ ; перенос множителя, числа
$A\cdot (B\pm C)=D$ $\Leftrightarrow$ $A\cdot B \pm A\cdot C=D$ ; $7x^2-3m(5-4C)=D$ $\Leftrightarrow$ $7x^2-15m+12mC=D$ Раскрытие скобок
$A\cdot B\cdot C=0$ $\Leftrightarrow$ [ $A=0$, $B=0$, $C=0$ ] ; $(x-m)(A+2x)(3x-12)=0$ $\Leftrightarrow$ [ $x-m=0$, $A+2x=0$, $3x-12=0$ ] ; $(A+2)(x^2-25)=0$ $\Leftrightarrow$ [ $A=-2$, $x^2=25$ ] ; Факторизация: произведение = 0 $\Leftrightarrow$ случаи ... множители = 0
Очевидные эквивалентности, переход к равенствам по одинаковости:
$\frac{8}{A}=\frac{8}{B}$ $\Rightarrow$ $A=B$ ; $\frac{1}{A}=B$ $\Rightarrow$ $A=\frac{1}{B}$
$\frac{A}{B}=\frac{m}{3}$ $\Rightarrow$ $\frac{B}{A}=\frac{3}{m}$ ; $\frac{A}{B}=\frac{m}{k}$ $\Rightarrow$ $\frac{A}{k}=\frac{B}{m}$ ;
$A^2=B^2$ $\Rightarrow$ $A=\pm B$ ; $A^2=C$ $\Rightarrow$ $A=\pm \sqrt C$
$A^3=B^3$ $\Rightarrow$ $A=B$ ; $A^4=B^4$ $\Rightarrow$ $A=\pm B$ ;
$\sqrt{A}=\sqrt{B}$ $\Rightarrow$ $A=B$ ; $\sqrt[3]{A}=\sqrt[3]{B}$ $\Rightarrow$ $A=B$ ;
$m^A=m^B$ $\Rightarrow$ $A=B$ ; $3^X=3^{-2,5}$ $\Rightarrow$ $X=-2,5$ ;
$\log_mA= \log_mB$ $\Rightarrow$ $A=B$ ; $\log_2(X)= \log_2(-3)$ $\Rightarrow$ $X=-3$ ;
$\sin X=\sin \phi$ $\Rightarrow$ $X= \phi+2\pi n$ , $X= \pi-\phi+2\pi n$ ; $\tg X=\tg \phi$ $\Rightarrow$ $X= \phi+\pi n$
$\cos X=\sin \phi$ $\Rightarrow$ $X= \phi+2\pi n$ , $X=-\phi+2\pi n$ ; $\ctg X=\ctg \phi$ $\Rightarrow$ $X= \phi+\pi n$
Квадратные уравнения, эквивалентные преобразования: скобки, группирования, приведение, дробные коэффициенты Произвольное квадратное уравнение можно привести к стандартному виду с помощью эквивалентных преобразований: "перенос слагаемых" , "умножение на число", "перенос множителя", "открытие скобок" , "приведение подобных".
Решение квадратного: $ax^2+bx+c=0$ , $D=b^2-4ac$ - Дискриминант . I. $D < 0$ - нет корней II. $D=0$ - один корень: $x=\frac{-b}{2a}$ III. $D > 0$ - два корня: $x=\frac{-b+\sqrt{D}}{2a}$, $x=\frac{-b-\sqrt{D}}{2a}$
Упрощенные формулы для приведенного квадратного $x^2+bx+c=0$ $\Rightarrow$ $D=p^2-q$ ; $x=-p+\sqrt{D}$ ; $x=-p-\sqrt{D}$
Неполные квадратные: $ax^2+bx=0$ , $ax^2=cx$ , $ax^2=c$ $ax^2+bx=0$ $\Rightarrow$ [$x=0, ax+b=0$] ; $x^2=a$ $\Rightarrow$ $x=\pm \sqrt{a}$ ; $ax^2=cx$ $\Rightarrow$ [$x=0, ax=c$]; $ax^2=c$ $\Rightarrow$ [$x=\sqrt{\frac{c}{a}}, x=-\sqrt{\frac{c}{a}}$] ;
Уравнение "дробь = дробь" $\frac{A\left(x\right)}{B\left(x\right)}=\frac{C\left(x\right)}{D\left(x\right)}$ $\Rightarrow$ $\Rightarrow$ $A\left(x\right)\cdot D\left(x\right)=C\left(x\right)\cdot B\left(x\right)$ , $B\left(x\right)\ne0$ $D\left(x\right)\ne0$ .
Свойство пропорции: $\frac{A}{B}=\frac{C}{D}$ $\Rightarrow$ $A\cdot D=C\cdot B$. Сложения дробей $\frac{A}{B}\pm\frac{C}{D}=\frac{A\cdot D\pm C\cdot B}{B\cdot D}$ $\frac{A}{B}\pm K=\frac{A\pm K\cdot B}{B}$
Уравнение "дробь = 0" : $\frac{A\left(x\right)}{B\left(x\right)}=0$ эквивалентно $\Leftrightarrow$ $A\left(x\right)=0$ $B\left(x\right)\ne0$ . числитель $= 0$, знаменатель $\ne0$.
Возведения в квадрат обеих частей:: $\sqrt{X}=C$ $\Rightarrow $ $X=C^2$ при условии: $C\ge0$ , $C$ - неотрицательна
Извлечение корня от обеих частей степенного:: $A^{2n+1}=m^{2n+1}$ $\Rightarrow $ $A=m$ ; $A^{2n}=m^{2n}$ $\Rightarrow $ $A=m$, $A=-m$ ;
Возведения в куб (в степень) обеих частей уравнения с радикалом:: $\sqrt[3]{X}=C$ $\Leftrightarrow$ $X=C^3$ $\sqrt[5]{X}=C$ $\Leftrightarrow$ $X=C^5$
Показательное уравнение: $a^{f\left(x\right)}=a^n$ $\Leftrightarrow$ $f\left(x\right)=n$ равенство показателей при одинаковых основаниях.
Логарифмическое уравнение: $\log_af\left(x\right)=c$ $\Rightarrow$ $f\left(x\right)=a^c$ $\log_af\left(x\right)=\log_ag\left(x\right)$ $\Rightarrow$ $f\left(x\right)=g\left(x\right)$
Тригонометрическое уравнение, серии решений через arc - числа в правой части:
$\sin f\left(x\right)=c$ , $\left|c\right|\le1$ $\Rightarrow$ $f(x)=\arcsin\left(c\right)+2\cdot\pi\cdot n$ , $f(x)=\pi-\arcsin\left(c\right)+2\cdot\pi\cdot k$ , $n\in Z$, $k\in Z$
$\cos f\left(x\right)=c$, $\left|c\right|\le1$ $\Rightarrow$ $f(x)=-\arccos\left(c\right)+2\cdot\pi\cdot n$ , $f(x)=+\arccos\left(c\right)+2\cdot\pi\cdot k$ , $n\in Z$, $k\in Z$
$\tg f(x)=c$ $\Leftrightarrow$ $f(x)=\arctg\left(c\right)+\pi n$ ; $\ctg f(x)=c$ $\Leftrightarrow$ $f(x)=\arcctg\left(c\right)+\pi n$
Графическое решение уравнения $f(x)=g(x)$: корни как абсциссы точек пересечения графиков $y=f(x)$ и $y=f(x)$.
I. Тестирование: ЕГЭ - профильный, задания №6, Уравнения, простые:
Развернутое решение уравнений пишите в Листах №71, №72 . Каждый шаг в отдельной строке, полноценное решение уравнения. Интерактивная проверка каждого шага решения. Новое уравнение ? Обновите лист.
II. Тема: Линейное уравнение Примеры решений:
1. $ax=b$ $\Rightarrow$ $x=\frac{b}{a}$ 2. $ax+b=c$ $\Rightarrow$ $ax=c-b$ $\Rightarrow$ $x=\frac{c-b}{a}$
3. $2x=10$ $\Rightarrow$ $\frac{2x}{2}=\frac{10}{2}$ $x=5$ Перенос множителя: - поделим обе части на $2$
4. $12x+5=-7x+9$ $\Rightarrow$ $12x=-7x+9-5$ $12x+7x=4$ Переносы слагаемых: $\Rightarrow$ $19x=4$ $x=\frac{4}{19}$
5. $7\left(x-3\right)=2x-5\left(x-4\right)-1$ $\Rightarrow$ $7x-21=2x-5x+20-1$ раскроем скобки; $7x-2x+5x=21+20-1$ $10x=40$ $x=\frac{40}{10}$ $x=4$
переносить можно и слагаемые, и коэффициенты-множители: слагаемые неизвестные и числа переносятся на другую сторону с противоположным знаком; множители переносятся на другую сторону делением, делители переносятся умножением.
III. Тема: Квадратное уравнение стандартный или канонический вид : $a\cdot x^2+b\cdot x+c=0$
Решение канонического $ax^2+bx+c=0$ , $D=b^2-4ac$ - Дискриминант . I. $D < 0$ - при отрицательном дискриминанте нет корней II. $D=0$ - один корень: $x=\frac{-b}{2a}$ III. $D > 0$ - два корня: $x=\frac{-b+\sqrt{D}}{2a}$, $x=\frac{-b-\sqrt{D}}{2a}$
1. $x^2-3x-4=0$ $\Rightarrow$ $D=b^2-4ac=\left(-3\right)^2-4\cdot 1\cdot\left(-4\right)=9+16=25$ $x=\frac{-\left(-3\right)+5}{2}=\frac{3+5}{2}=4$ и $x=\frac{-\left(-3\right)-5}{2}=\frac{3-5}{2}=-1$
2. $7x^2-2x-7=0$ $\Rightarrow$ $D=b^2-4ac=\left(-2\right)^2-4\cdot7\cdot\left(-7\right)=4+196=200.$ $x=\frac{2+\sqrt{200}}{2\cdot7}=\frac{2+10\sqrt{2}}{2\cdot7}=\frac{1+5\sqrt{2}}{7}$ $x=\frac{1-5\sqrt{2}}{7}$
3. $-x^2+8x-3=0$ $\Rightarrow$ умножим всё на $(-1)$ $x^2-8x+3=0$ $x_1=4+\sqrt{13}$ , $x_2=4-\sqrt{13}$
4. $x-7-5x^2=3x^2+6x-10$ $\Rightarrow$ $-x-7-5x^2-3x^2-6x+10=0$ $-2x^2-5x+3=0$ $x_1=\frac{1}{2}$ ; $x_2=-3$
5. $11x-\left(3x+1\right)\left(6-2x\right)=5\left(x^2-2\right)+18$ $\Rightarrow$ $11x-\left(18x+6-6x^2-2x\right)=5x^2-10+18$ $11x-16x-6+6x^2=5x^2+8$ $-5x-6+6x^2-5x^2-8=0$ $x^2-5x-14=0$ $x_1=2$ ; $x_2=-7$
6. $-0,3x^2+0,8x-1,7=0$ $\Rightarrow$ Обе части домножим на $10$ (или $100$), запятые уйдут $-10\left(-0,3x^2+0,8x-1,7\right)=\left(-10\right)\cdot0$ $\Leftrightarrow$ $3x^2-8x+17=0$ ......
7. $\frac{3}{4}x^2-\frac{5}{6}x-\frac{7}{3}=0$ $\Rightarrow$ домножим на кратное всех знаменателей, $12$ Дроби исчезнут! $12\cdot\left(\frac{3}{4}x^2-\frac{5}{6}x-\frac{7}{3}\right)=12\cdot0$ $\Leftrightarrow$ $9x^2-10x-14=0$. .....
8. Упрощенные формулы для приведенного квадратного $x^2+bx+c=0$ $\Rightarrow$ $D=p^2-q$ ; $x=-p+\sqrt{D}$ ; $x=-p-\sqrt{D}$
9. $x^2+6x-7=0$ четный $2p = 6$ $\Rightarrow$ $p = 3$ , $D=3^2-(-7)=9+7=16$ $x_1=-p+\sqrt{D}=-3+4=1$ , $x_2=-p-\sqrt{D}=-3-4=-7$ Ответ: $x_1=1$ , $x_2=-7$
10. $x^2-6x+3=0$ $p =-3$ . упрощенную $x_1=-p+\sqrt{p^2-q}=3+\sqrt{9-3}=3+\sqrt{6}$ , $x_2=-p-\sqrt{p^2-q}=3-\sqrt{6}$ Ответ: $x_1=3+\sqrt{6}$ , $x_2=3-\sqrt{6}$
11. $x^2-8x+26=0$ $p=-4$ ; $q=26$ $D=p^2-q=\left(-4\right)^2-26=16-26=-10 < 0 $ корней нет!
12. $-x^2+8x-3=0$ умножим всё на $(-1)$ $x^2-8x+3=0$ . $D=\left(-4\right)^2-3=13$, Ответ: $x_1=4+\sqrt{13}$ , $x_2=4-\sqrt{13}$
Решение неполных квадратных уравнений: $ax^2+bx=0$ , $ax^2=cx$ , $ax^2=c$
Для простейшего уравнения $x^2=a$ решение: $x_1=\sqrt{a}$ ; $x_2=-\sqrt{a}$ , если $a$ - неотрицательное число.
1. $6x^2–2x=0$ вынесем общий множитель за скобки: $2x\cdot(3x – 1)=0$ ; распад: $2x=0$ $\Rightarrow$ $x=0$ ; $3x–1=0$ $\Rightarrow$ $x=\frac{1}{3}$ . ответ: $x_1=0$ ; $x_2=\frac{1}{3}$
2. $50x^2-7x=0$ $\Rightarrow$ $x\cdot\left(50x-7\right)=0$. $x=0$ ; 2-й: $50x-7=0$ ... $x=\frac{7}{50}$
3. $9x^2-16=0$ Разложим на множители по формуле "разность квадратОВ": $(3x-4)\cdot\left(3x+4\right)=0$ два случая - $3x-4=0$ $\Rightarrow$ $3x=4$ . $3x+4=0$ $\Rightarrow$ $3x=-4$
4. $2x^2=72$ $\Rightarrow$ $x^2=\frac{72}{2}$ $x^2=36$ ответ: $x_1=-6$ ; $x_2=6$
5. $4x^2=13$ $\Rightarrow$ $x^2=\frac{13}{4}$ ответ: $x_1=-\frac{\sqrt{13}}{2}$ ; $x_2=\frac{\sqrt{13}}{2}$
Пример 6.: Решить факторизованное уравнение $(3-x)\cdot\left(4x+6x^2\right)\cdot\left(x^2-1\right)=0$
- Произведение скобок равно нулю. Для каждого множителя напишем уравнение обнуления: Каждое "скобка = 0" и решим каждое.
- №1 $x^2-1=0$ $\Rightarrow$ $(x-1)(x+1)=0$ $x-1=0$ $x+1=0$ $x=-1$ $x=1$
- №2 $4x+6x^2=0$ $\Rightarrow$ $2x(2x+3)=0$ $x=0$ $2x+3=0$ $x=-\frac{3}{2}$
- №3 $3-x=0$ $\Rightarrow$ $x=3$ ответ: $x=3$ $x=0$ $x=-1,5$ $x=-1$ $x=1$
IV. Тема: Дробно-рациональное уравнение
Уравнение "дробь = дробь" $\frac{A\left(x\right)}{B\left(x\right)}=\frac{C\left(x\right)}{D\left(x\right)}$ решается переходом к квадратному по свойству пропорций $\Rightarrow$ $A\left(x\right)\cdot D\left(x\right)=C\left(x\right)\cdot B\left(x\right)$ .
Свойство пропорции: если $\frac{A}{B}=\frac{C}{D}$ , тогда $A\cdot D=C\cdot B$. крест-накрест
Если дробь = 0 " .... вся дробь равна нулю значит, числитель = 0. Как иначе!
Уравнение "дробь = 0" : $\frac{A\left(x\right)}{B\left(x\right)}=0$ эквивалентно $\Leftrightarrow$ $A\left(x\right)=0$ $B\left(x\right)\ne0$ . числитель $= 0$, знаменатель $\ne0$.
Правило сложения алгебраических дробей $\frac{A}{B}\pm\frac{C}{D}=\frac{A\cdot D\pm C\cdot B}{B\cdot D}$ $\frac{A}{B}\pm K=\frac{A\pm K\cdot B}{B}$
$\frac{\left(-4x+7\right)\left(2x-3\right)-\left(15-6x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-3\right)}=\left(-4x+7\right)\left(2x-3\right)-\left(15-6x\right)\left(2x-1\right)$ $\frac{2x+4}{2x-1}-3=\frac{2x+4-3\cdot\left(2x-1\right)}{2x-1}=\frac{15-6x}{2x-3}$ .
1. $\frac{3-2x}{x+2}=\frac{30}{5-x}$ $\Leftrightarrow$ $\left(3-2x\right)\left(5-x\right)=30\cdot\left(x+2\right)$ $15-3x-10x+2x^2=30x+60$ $2x^2-43x-45=0$ $x_1=22,5$; $x_2=-1$ .
2. $\frac{x^2-3x}{7-2x}=\frac{x+1}{5}$ $\Rightarrow$ $\left(x^2-3x\right)\cdot5=\left(x+1\right)\cdot\left(7-2x\right)$ .
3. $\frac{x^2-17}{5-x}=-1$ $\Rightarrow$ $x^2-17=-1\cdot\left(5-x\right)$
4. $\frac{x^2-5x+6}{x^2-9}=0$ $\Leftrightarrow$ ОДЗ $x^2-9\ne0$. числитель = 0 $x^2-5x+6=0$ $x_1=2$ $x_2=3$ -ложное ОДЗ , ответ: $x=2$
5. $\frac{x^2-7}{x-3}=\frac{2}{x-3}+12$ ОДЗ $x-3\ne0$ к общему знаменателю $\frac{x^2-7}{x-3}=\frac{2}{x-3}+\frac{12\left(x-3\right)}{x-3}$ , $\frac{x^2-7}{x-3}=\frac{2+12\left(x-3\right)}{x-3}$ $x^2-12x+27=0$ $\Leftrightarrow$ $x_1=3$ ; $x_2=9$ . $x=3$ не удовлетворяет ОДЗ , ответ: $x=9$
6. $\frac{2x+4}{2x-1}-3=\frac{15-6x}{2x-3}$ ОДЗ $2x-1\ne0$ $2x-3\ne0$ $\frac{2x+4}{2x-1}-\frac{3}{1}=\frac{15-6x}{2x-3}$ и применим правило сложения алгебраических дробей $\frac{-4x+7}{2x-1}=\frac{15-6x}{2x-3}$ , $\frac{-4x+7}{2x-1}-\frac{15-6x}{2x-3}=0$ $\frac{\left(-4x+7\right)\left(2x-3\right)-\left(15-6x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-3\right)}=0$ $\left(-4x+7\right)\left(2x-3\right)-\left(15-6x\right)\left(2x-1\right)=0$ , $-8x^2+12x+14x-21-30x+15+12x^2-6x=0$ , $4x^2-10x-6=0$ $\Rightarrow$ $2x^2-5x-3=0$ . ответ: $x_1=3$ $x_2=-\frac{1}{2}$ .
V. Тема: Степенные уравнения
Извлечение корня от обеих частей степенного уравнения:: $A^3=-27$ $\Rightarrow $ $A=-3$ ; $A^{2n+1}=m^{2n+1}$ $\Rightarrow $ $A=m$ ; $A^{2n}=m^{2n}$ $\Rightarrow $ $A=m$, $A=-m$ ; $A^5=4^5$ $\Rightarrow $ $A=4$ ; $A^3=-\frac{1}{8}$ $\Rightarrow $ $A=-\frac{1}{2}$ ; $(\frac{1}{A})^3=125$ $\Rightarrow $ $A=\frac{1}{5}$
1. $(2x+3)^3=-125$ $\Rightarrow$ $(2x+3)^3=(-5)^3$ , степени равны $\to$ основания равны, $2x+3=-5$, ответ: $x=-4$.
2. $(7-x)^5=-\frac{1}{32}$ $\Rightarrow$ $(7-x)^5=(-\frac{1}{2})^5$, равенство оснований $\to$ $7-x=-\frac{1}{2}$, ответ: $x=7,5$
3. $(\frac{1}{x+2})^4=81$ $\Rightarrow$ $(\frac{1}{x+2})^4=3^4$ равенство одинаковых степеней, $\Leftrightarrow$ извлечение корня четной степени, два случая: $\frac{1}{x+2}=\pm 3$ перевернем обе части, обратные: 1): $x+2=\frac{1}{3}$ , $x=-\frac{5}{3}$ 2): $x+2=-\frac{1}{3}$ , $x=-\frac{7}{3}$ . ответы: $x=-\frac{5}{3}$ , $x=-\frac{7}{3}$
4. $0,1\cdot (1-x)^3=-2\frac{7}{10}$ $\Rightarrow$ $\frac{1}{10}\cdot (1-x)^3=-\frac{2\cdot +7}{10}$ $1\cdot (1-x)^3=-27$ , $1\cdot (1-x)^3=-3^3$ $1-x=-3$ ответ: $x=4$
VI. Тема: Иррациональные уравнения, радикалы
Возведения в квадрат обеих частей уравнения:: $\sqrt{X}=C$ $\Rightarrow $ $X=C^2$ при условии: $C\ge0$ , $C$ - неотрицательна
1. $\sqrt{\frac{3+12x}{2x-1}}=3$ $\left(\sqrt{\frac{3+12x}{2x-1}}\right)^2=\left(3\right)^2$ $\frac{3+12x}{2x-1}=9$ $3+12x=9\cdot\left(2x-1\right)$ $\Leftrightarrow$ $12=18x-12x$ ответ: $x=2$
2. $\sqrt{6-4x-x^2}=-3-2x$ ОДЗ $6-4x-x^2\ge0$ $\left(\sqrt{6-4x-x^2}\right)^2=\left(-3-2x\right)^2$ при условии $-3-2x\ge0$ $6-4x-x^2=9+12x+4x^2$ $5x^2+16x+3=0$. $x=-3$ , $x=-0.2$ ложное решение (при условии не выполняется). ответ: $x=-3$
3. $\sqrt{5-x^2}-2x=3-x$ $\Rightarrow$ ОДЗ $5-x^2\ge0$ $\Rightarrow$ $\left(\sqrt{5-x^2}\right)^2=\left(x+3\right)^2$ при $x+3\ge0$ $\Rightarrow$ $5-x^2=x^2+6x+9$ $\Leftrightarrow$ $2x^2+6x+4=0$ $\Leftrightarrow$ $x^2+3x+2=0$ $\Rightarrow$ $x=-1$ , $x=-2$. ответ: $x=-1$ , $x=-2$ оба корня истинные, т.к. проходят ОДЗ и "при условии".
4. $\sqrt{2-x+x^2}-\sqrt{6-2x}=0$ ОДЗ: $2-x+x^2\ge0$ ; $6-2x\ge0$ $\Rightarrow$ $\sqrt{2-x+x^2}=\sqrt{6-2x}$ $\Leftrightarrow$ $2-x+x^2=6-2x$ $\Leftrightarrow$ $x^2+x-4=0$ $\Leftrightarrow$ $x=\frac{-1-\sqrt{17}}{2}$ $x=\frac{-1+\sqrt{17}}{2}$ . бракуем ложные?
Возведения в куб (в степень) обеих частей уравнения с радикалом:: $\sqrt[3]{X}=C$ $\Leftrightarrow$ $X=C^3$ $\sqrt[5]{X}=C$ $\Leftrightarrow$ $X=C^5$
1. $\sqrt[3]{2x-10}=-4$ $\Leftrightarrow$ $3x-10=(-4)^3$ , $3x-10=-64$ , ответ: $x=-18$
2. $\sqrt[3]{5-x}=2$ $\Leftrightarrow$ $5-x=(2)^3$ , $5-x=8$ , ответ: $x=-3$
3. $\sqrt[3]{\frac{1}{x+1}}=-5$ $\Leftrightarrow$ $\frac{1}{x+1}=-125$ , $x+1=-\frac{1}{125}$ , ответ: $x=-\frac{126}{125}$
VII. Тема: Показательные уравнения
Формулы, свойства степеней:
- Умножение степеней - основание одинаковые, показатели складываются: $a^m\cdot a^n=a^{m+n}$ $\Leftrightarrow$ $a^{x+y}=a^x\cdot a^y$ ;
- $\frac{a^m}{a^n}=a^{m-n}$ $\Leftrightarrow$ $a^{x-y}=\frac{a^x}{a^y}$ Делении степеней с одинаковыми основаниями - основание прежнее, показатели вычитаются.
- $\left(a^x\right)^y=a^{xy}$ $\Leftrightarrow$ $a^{mn}=\left(a^m\right)^n$ Возведении степени в степень показатели перемножаются. И наоборот!
- $\left(a\cdot b\right)^x=a^x\cdot b^x$ $\Leftrightarrow$ $a^n\cdot b^n=\left(a\cdot b\right)^n$ Возведение в степень произведения - в эту степень возводится каждый множитель:
- $\left(\frac{a}{b}\right)^x=\frac{a^x}{b^x}$ $\Leftrightarrow$ $\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n$ Возведение в степень дроби в эту степень возводится числитель дроби и знаменатель . Деление?
- Дробная степень: $a^{\frac{x}{y}}=\left(\sqrt[y]{a}\right)^x$ ; $\sqrt[m]{a^n}=a^{\frac{n}{m}}$ Знаменатель как корень. Числитель как степень.
- Отрицательная степень $\Leftrightarrow$ обратная степень : $a^{-x}=\frac{1}{a^x}$ ; $\left(\frac{a}{b}\right)^{-x}=\left(\frac{b}{a}\right)^x$
Простейшее показательное $a^{f\left(x\right)}=a^n$ $\Leftrightarrow$ $f\left(x\right)=n$ равенство показателей при одинаковых основаниях.
1. $8^{3-x}=4$ $\Rightarrow$ $\left(2^3\right)^{3-x}=2^2$ , $2^{3\cdot\left(3-x\right)}=2^2$ , $3\cdot\left(3-x\right)=2$ , $3x=7$ $\Leftrightarrow$ $x=\frac{7}{3}$ .
2. $5^{-3x+1}=0.2^{\frac{1}{3}}\cdot\sqrt{125}$ $\Rightarrow$ $5^{-3x+1}=\left(\frac{1}{5}\right)^{\frac{1}{3}}\cdot\sqrt{5^3}$ $5^{-3x+1}=5^{-\frac{1}{3}}\cdot5^{\frac{3}{2}}$ , $5^{-3x+1}=5^{-\frac{1}{3}+\frac{3}{2}}$ , $5^{-3x+1}=5^{\frac{7}{6}}$ , $-3x+1=\frac{7}{6}$ ответ: $x=-\frac{1}{18}$
3. $5^{x^2-1}=3^{x^2-1}$ $\Rightarrow$ $\frac{5^{x^2-1}}{3^{x^2-1}}=1$ , $\left(\frac{5}{3}\right)^{x^2-1}=1$ , $\left(\frac{5}{3}\right)^{x^2-1}=\left(\frac{5}{3}\right)^0$ , $x^2-1=0$ ответ: $x=1$ , $x=-1$ .
VIII. Тема: Логарифмические уравнения
Формулы, свойства логарифмов
- Основное тождество $\log_ab=n$ $\Leftrightarrow$ $b=a^n$ $a^{\log b_a}=b$ Логарифм есть показатель степени.
- сумма логарифмов $\log_ax+\log_ay=\log_axy$ логарифм произведения. разность логарифмов $\log_ax-\log_ay=\log_a\frac{x}{y}$
- формула замены основания: $\log_ab=\frac{1}{\log_ba}$ обратное логарифма $\frac{1}{\log_ba}=\log_ab$
- Вынос показателя степени аргумента: $\log_a\left(b^c\right)=c\cdot\log_ab$ ; и наоборот: множитель заносится внутрь $c\cdot\log_ab=\log_a\left(b^c\right)$
- Вынос показателя степени основания: $\log_{\left(a^n\right)}b=\frac{1}{n}\cdot\log_ab$ ; множитель заносится как корень основания $n\cdot\log_ab=\log_{\left(a^{\frac{1}{n}}\right)}b$
- Переход к новому основанию: $\log_ab=\frac{\log_xb}{\log_xa}$ ; отношение двух логарифмов с одинаковым основанием $\frac{\log_xb}{\log_xa}=\log_ab$
- Перекрестное произведение логарифмов: $\log_ax\cdot\log_xb=\log_ab$ ; аргумент одного равен основанию другого, как будто "сокращение" .
- Универсальная формула для степеней внутри логарифма: $\log_{\left(a^n\right)}\left(b^m\right)=\frac{m}{n}\cdot\log_ab$ ;
- Транзит, логарифм в показателе: $a^{\log_xb}=b^{\log_xa}$ $2^{\log_83}=3^{\log_82}$
Решение простейшего логарифмического: $\log_af\left(x\right)=c$ $\Rightarrow$ $f\left(x\right)=a^c$ $\log_af\left(x\right)=\log_ag\left(x\right)$ $\Rightarrow$ $f\left(x\right)=g\left(x\right)$
При равенстве двух логарифмов с одним и тем же основанием, приравниваем аргументы этих логарифмов.
1. $\log_{49}\left(2x-1\right)=0.5$ О.Д.З. $2x-1 > 0$ "вскроем логарифм" по основному тождеству: аргумент уравняется с "основанием в степени правое число", $\Rightarrow$ $2x-1=49^{0.5}$ $\Rightarrow$ $2x=7+1$ $\Rightarrow$ $x=4$ проверка О.Д.З. , удовлетворяет. Ответ: $x=4$
2. $\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}36=\log_{\frac{1}{3}}10$ О.Д.З. $x > 0$ $\log_{\frac{1}{3}}\frac{x}{36}=\log_{\frac{1}{3}}10$ $\frac{x}{36}=\left(\frac{1}{3}\right)^{\log_{\frac{1}{3}}10}$ $\frac{x}{36}=10$ , проверим О.Д.З., Ответ: $x=360$
3. $\log_{0.6}\left(2x^2-3x+1\right)=\log_{0.6}\left(13-x\right)$ О.Д.З. $2x^2-3x+1 > 0$ $13 > x$ _ приравнять аргументы: $2x^2-3x+1=13-x$ , $x^2-x-6=0$ , ОДЗ ? , Ответ: $x_1=-2$ ; $x_2=3$
IX. Тема: Тригонометрические уравнения
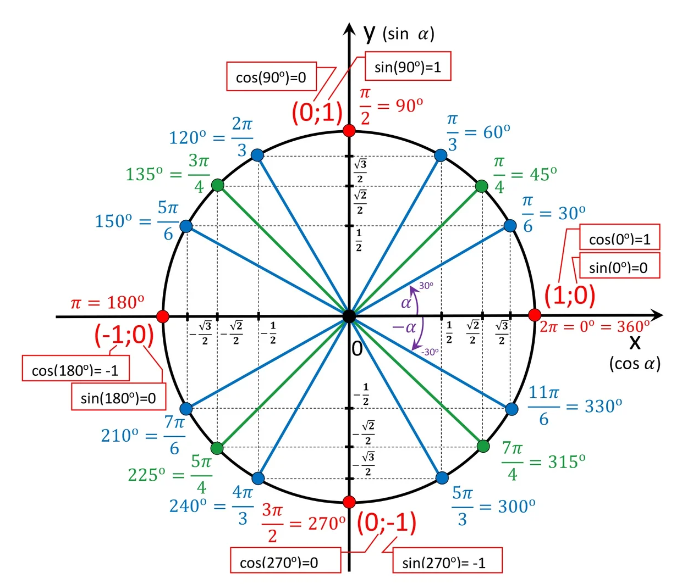
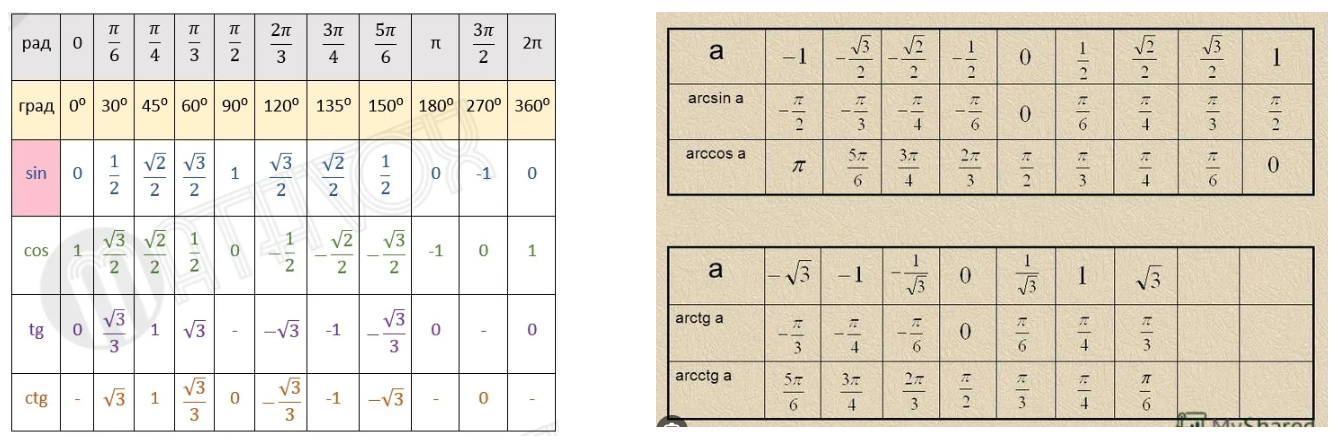
Решения простейших тригонометрических уравнений. Таблицы arc - функций.
$\sin f\left(x\right)=c$ , $\left|c\right|\le1$ $\Rightarrow$ $f(x)=\arcsin\left(c\right)+2\cdot\pi\cdot n$ , $f(x)=\pi-\arcsin\left(c\right)+2\cdot\pi\cdot k$ , $n\in Z$, $k\in Z$
$\cos f\left(x\right)=c$, $\left|c\right|\le1$ $\Rightarrow$ $f(x)=-\arccos\left(c\right)+2\cdot\pi\cdot n$ , $f(x)=+\arccos\left(c\right)+2\cdot\pi\cdot k$ , $n\in Z$, $k\in Z$
$\tg f(x)=c$ $\Leftrightarrow$ $f(x)=\arctg\left(c\right)+\pi n$ ; $\ctg f(x)=c$ $\Leftrightarrow$ $f(x)=\arcctg\left(c\right)+\pi n$

Пример 1.: Решить уравнение $\sin \left(\frac{\pi \left(7-2x\right)}{6}\right)=-\frac{\sqrt{3}}{2}$ . В ответе указать наибольший отрицательный корень.
- Для конструирования серий решений нужен арксинус правой части: $\arcsin (-\frac{\sqrt{3}}{2})=-\frac{\pi}{3}$
- 1-ая серия: $\frac{\pi \left(7-2x\right)}{6}=-\frac{\pi}{3}+2\cdot\pi\cdot n$ $\Leftrightarrow$ сократим на общий множитель $\pi$ : $\Leftrightarrow$ $\frac{7-2x}{6}=-\frac{1}{3}+2n$
- $\frac{7-2x}{6}=-\frac{1}{3}+2n$ $\Leftrightarrow$ $7-2x=-2+12n$ $\Leftrightarrow$ $2x=9-12n$ $\Leftrightarrow$ $x=\frac{5-12n}{2}$
- Конкретные корни: $n=0\to x=\frac{5}{2}$ ; $n=1\to x=-\frac{7}{2}$ ; $n=-1\to x=\frac{17}{2}$ ; $n=2\to x=-\frac{19}{2}$
- 2-ая серия: $\frac{\pi \left(7-2x\right)}{6}=\pi-(-\frac{\pi}{3})+2\cdot\pi\cdot k$ $\Leftrightarrow$ сократим на общий множитель $\pi$ : $\Leftrightarrow$ $\frac{7-2x}{6}=1+\frac{1}{3}+2k$
- $\frac{7-2x}{6}=1+\frac{1}{3}+2k$ $\Leftrightarrow$ $7-2x=8+12k$ $\Leftrightarrow$ $2x=-1-12k$ $\Leftrightarrow$ $x=\frac{-1-12k}{2}$
- Конкретные корни: $n=0\to x=-\frac{1}{2}$ ; $n=1\to x=-\frac{13}{2}$ ; $n=-1\to x=\frac{11}{2}$ ; $n=2\to x=-\frac{25}{2}$
- Среди всех полученнных в обеих сериях корней выберем наибольшее отрицательное: $x=-\frac{1}{2}=-0,5$.
- Еще вопрос: Найти наименьшее положительное решение. Ответ: $x=\frac{5}{2}=2,5$





I. Упражнения по темам несложных уравнений:
Линейное уравнение
Уравнение вида $ax=b$ , где $a$ и $b$ - числа, $x$ - переменная , называют линейным уравнением .
- линейное уравнение $ax=b$ $\Rightarrow$ kорень этого уравнения $x=\frac{b}{a}$.
- подробнее здесь II . § 5. Линейные уравнения.
Пример 1 решить простейшее линейное уравнение $2x=10$
- Чему же равен $x$ ? Какое число на месте $x$ уравняет обе части уравнения? $\frac{2x}{2}=\frac{10}{2}$ поделим обе части на $2$; чтобы $x$ остался без коэффициента: $x=5$ после сокращения дробей в обеих частях, получаем чему равен $x$. Проверка: подставим найденное число $5$ в уравнение, т.е напишем его вместо неизвестного $x$ : $2\cdot5=10$ $10=10$ Найденное число выравнивает левую и правую части, значит является корнем уравнения. Ответ: $x=5$
Пример 2 решить линейное уравнение $12x+5=-7x+9$
- $12x+5-5=-7x+9-5$ хотим избавиться в левой части от числа $-5$ : добавим такое же к обеим частям;
- $12x=-7x+9-5$ в левой части число исчезло, а в правой оно появилось, но с противоположным знаком
- так мы провели операцию переноса числа из одной части в другую ;
- $12x=-7x+4$ немного укоротим наше уравнение : произведем вычисление в правой части ;
- $12x+7x=-7x+4+7x$ планируем избавиться от неизвестного в правой части: добавим по $7x$ к обеим частям;
- $12x+7x=4$ справа $-7x$ исчезло, но "появилось" слева со знаком "+ ": это и есть перенос из одной части в другую;
- $x\cdot\left(12+7\right)=4$ в левой части вынесем общий множитель $x$ за скобки ;
- $19x=4$ вычислим значение скобки;
- $\frac{19x}{19}=\frac{4}{19}$ чтобы избавиться от коэффициента при $x$ разделим обе части на $19$ ;
- $x=\frac{4}{19}$ сократим дробь слева, так найдем чему равно неизвестное уравнения. Ответ: $x=\frac{4}{19}$ .
Пример 3 линейное уравнение со скобками $7\left(x-3\right)=2x-5\left(x-4\right)-1$
- $7x-21=2x-5x+20-1$ раскроем скобки; $7x-2x+5x=21+20-1$ перенесем все неизвестные в левую часть, а числа - в правую; $10x=40$ приведем подобные члены по обеим частям; $x=\frac{40}{10}$ разделим обе стороны на $10$ , чтобы освободить $x$ от коэффициента - это действие еще называется "перенос множителя" ; Ответ: $x=4$
Aлгоритм решения линейного уравнения: шаг за шагом от исходного уравнения ....
I. переходим к равносильному (с тем же корнем), доходим до конечного вида "неизвестное = число"; II. корни уравнения не меняются, если перенести любое слагаемое из одной части в другую с противоположным знаком. III. корни уравнения не меняются, если обе части умножить или разделить на одно и то же отличное от нуля число.
переносить можно и слагаемые, и коэффициенты-множители
- слагаемые неизвестные и числа переносятся на другую сторону с противоположным знаком;
- множители переносятся на другую сторону делением, делители переносятся умножением.
Квадратное уравнение
стандартный или канонический вид : $a\cdot x^2+b\cdot x+c=0$ или $0=a\cdot x^2+b\cdot x+c$
Числа $a$ , $b$ , $c$ при неизвестном называются коэффициентами уравнения . У каждого свое название: $a$ называют квадратным (т.к. он при $x^2$) или первым коэффициентом ; $b$ называют линейным или вторым коэффициентом ; $c$ называют свободным членом уравнения (т.к. он свободен от неизвестного) Важно правильно определять коэффициенты! Особое внимание на знаки:
Определяем коэффициенты так: I. $0,2x^2+7x+13=0$ коэффициенты : $a=0,2$ $b=7$ $c=13$ II. $3x^2-5x+10=0$ коэффициенты : $a=3$ $b=-5$ минус! $c=10$ III. $x^2-\frac{1}{3}x-5=0$ коэффициенты : $a=1$; $b=-\frac{1}{3}$ $c=-5$ минус! IV. $16x^2-25=0$ коэффициенты : $a=16$ $b=0$ $c=-25$ минус! V. $-\frac{1}{6}x^2-\frac{2}{3}x=0$ коэффициенты : $a=-\frac{1}{6}$ $b=-\frac{2}{3}$ минус! $c=0$ . Внимание: если дано нестандартное уравнение, чтобы не ошибиться в определении коэффициентов, сначала перепишите его в стандартном виде :
Решения канонического квадратного уравнения. Дискриминант
Канонический вид $ax^2+bx+c=0$ , $a$, $b$, $c$ - коэффициенты уравнения. Формула, составленная $D=b^2-4ac$ называется Дискриминант . I. $D > 0$ - да, уравнение нужно решать и у него будет два корня . II. $D=0$ - да, уравнение нужно решать и у него будет один корень . III. $D < 0$ - нет, при отрицательном дискриминанте нет корней и решать уравнение не стоит! Замечание: Не всегда при извлечении корня из Дискриминанта получается целое число. В этом случае, решением уравнения будет дробное выражение с радикалом. Посмотрите внимательно, можно ли упростить полученное выражение ? Ответ должен быть всегда в сокращенном виде.
Формулы нахождения корней канонического квадратного уравнения:
- $D > 0$: "+" корень $x=\frac{-b+\sqrt{b^2-4ac}}{2a}$ или $x=\frac{-b+\sqrt{D}}{2a}$ ;
- $D > 0$: "-" корень $x=\frac{-b-\sqrt{b^2-4ac}}{2a}$ или $x=\frac{-b-\sqrt{D}}{2a}$ .
- Если $D=0$ , один корень $x=\frac{-b+0}{2\cdot a}=-\frac{b}{2a}$
Пример 5 $x^2-3x-4=0$
- Определяем коэффициенты уравнения: $a=1$ , $b=-3$ , $c=-4$ Найдем Дискриминант.
- Внимание! Чтобы не ошибиться c отрицательными коэффициентами, лучше заключить его в скобки:
- $D=b^2-4ac=\left(-3\right)^2-4\cdot 1\cdot\left(-4\right)=9+16=25$ Т.к. $D=25 > 0$ , значит уравнение имеет два корня ,
- корни по формулам : $x=\frac{-b+\sqrt{D}}{2a}=\frac{-\left(-3\right)+5}{2}=\frac{3+5}{2}=4$ и $x=\frac{-b-\sqrt{D}}{2a}=\frac{-\left(-3\right)-5}{2}=\frac{3-5}{2}=-1$ Ответ: $x=4$ ; $x=-1$
Пример 6: $7x^2-2x-7=0$
- коэффициенты: $a=7$ , $b=-2$ , $c=-7$ $D=b^2-4ac=\left(-2\right)^2-4\cdot7\cdot\left(-7\right)=4+196=200.$ $D=200 > 0$ , два корня :
- $D=b^2-4ac=\left(-2\right)^2-4\cdot7\cdot\left(-7\right)=4+196=200.$ Т.к. $D=200 > 0$ , значит уравнение имеет два корня :
- 1) $x=\frac{-b+\sqrt{D}}{2a}=\frac{2+\sqrt{200}}{2\cdot7}$ Внимание! ответ нужно давать всегда в сокращенном виде.
- из-под корня вынести множитель 10, после сокращение: $x=\frac{2+\sqrt{200}}{2\cdot7}=\frac{2+10\sqrt{2}}{2\cdot7}=\frac{1+5\sqrt{2}}{7}$;
- 2) $x=\frac{-b-\sqrt{D}}{2a}=\frac{1-5\sqrt{2}}{7}$ Ответ: $x=\frac{1+5\sqrt{2}}{7}$ ; $x=\frac{1-5\sqrt{2}}{7}$
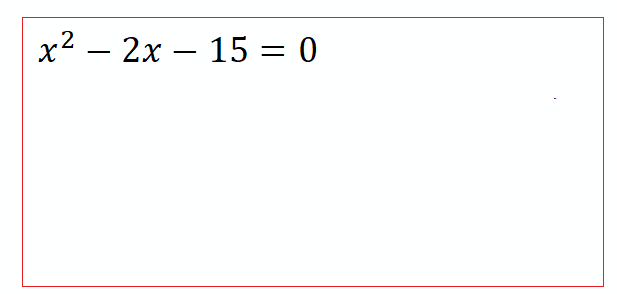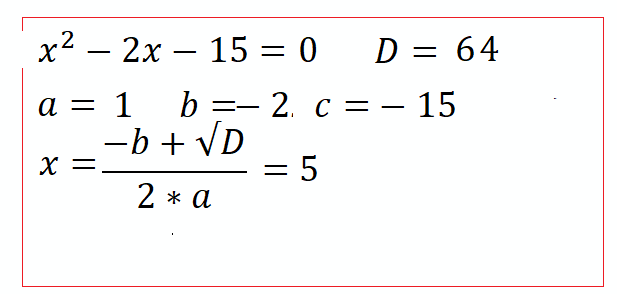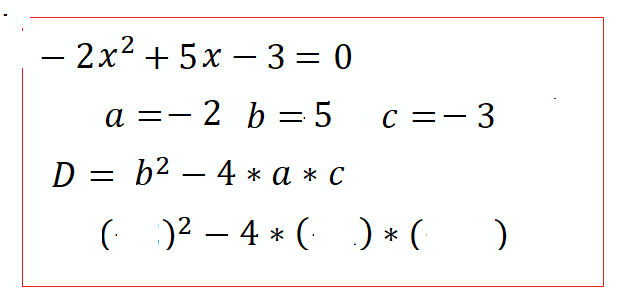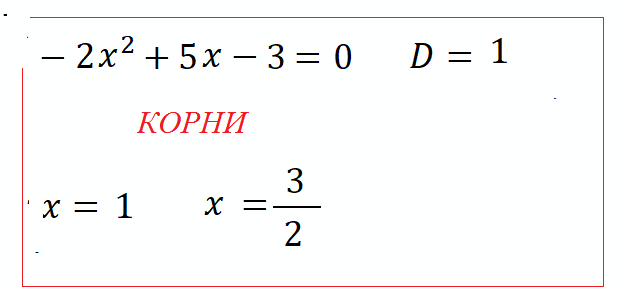


Квадратное называется приведенным , если коэффициент при $x^2$ равен единице: $x^2+bx+c=0$ . Если в таком уравнении $b$ - четное число , т.е. представляется как $2p$ , то приведенное $x^2+2px+q=0$ с четным линейным коэффициентом можно решать по упрощенным формулам .
- упрощенные формулы $D=p^2-q$ ; $x=-p+\sqrt{D}$ ; $x=-p-\sqrt{D}$
- $x=-p+\sqrt{p^2-q}$ ; $x=-p-\sqrt{p^2-q}$
Пример 7: Решение приведенного уравнения $x^2+6x-7=0$
- приведенном уравнении линейный четный $2p = 6$ $\Rightarrow$ $p = 3$ , $D=3^2-(-7)=9+7=16$
- $D>0$ $\Rightarrow$ два корня: $x_1=-p+\sqrt{D}=-3+4=1$ , $x_2=-p-\sqrt{D}=-3-4=-7$ Ответ: $x_1=1$ , $x_2=-7$
Пример 8: Решение уравнения $x^2-6x+3=0$
- $-6 =2p$ $\Rightarrow$ $p =-3$ . упрощенную $x_1=-p+\sqrt{p^2-q}=3+\sqrt{9-3}=3+\sqrt{6}$ , $x_2=-p-\sqrt{p^2-q}=3-\sqrt{6}$ Ответ: $x_1=3+\sqrt{6}$ , $x_2=3-\sqrt{6}$
Пример 9: Решение уравнения $x^2-8x+26=0$
- определим коэффициенты $2p=-8$ $\Rightarrow$ $p=-4$ ; $q=26$ и найдем дискриминант этого уравнения:
- $D=p^2-q=\left(-4\right)^2-26=16-26=-10 < 0 $ - он отрицательный, значит Ответ: корней нет!
Как быть, если в уравнении перед $x^2$ стоит "$-$" .
Пример 10: Решение уравнения $-x^2+8x-3=0$
- уравнение не является приведенным , первый коэффициент ($-1$) , умножим всё уравнение на $(-1)$
- $x^2-8x+3=0$ . теперь можно упрощенные формулы : $D=\left(-4\right)^2-3=13$, Ответ: $x_1=4+\sqrt{13}$ , $x_2=4-\sqrt{13}$
Квадратные уравнения, эквивалентные преобразования: скобки, группирования, приведение, дробные коэффициенты
- Произвольное квадратное уравнение можно привести к стандартному виду с помощью эквивалентных преобразований: "перенос слагаемых" , "умножение на число", "перенос множителя", "открытие скобок" , "приведение подобных".
Пример 11: Решить уравнение $x-7-5x^2=3x^2+6x-10$
- все слагаемые влево $-x-7-5x^2-3x^2-6x+10=0$ , выполним перестановку, сгруппируем подобные слагаемые $-5x^2-3x^2+x-6x-7+10=0$ ,
- приведем подобные $-2x^2-5x+3=0$ , умножим на "$-1$", стандартный вид : $2x^2+5x-3=0$
- Дискриминант $D=b^2-4ac=25+4\cdot2\cdot3=49$ по формулам корней $x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-5+\sqrt{49}}{2\cdot2}=\frac{-5+7}{4}=\frac{1}{2}$ ; $x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-5-7}{4}=-3$ Ответ: $x_1=\frac{1}{2}$ ; $x_2=-3$.
Пример 12: Решить уравнение $11x-\left(3x+1\right)\left(6-2x\right)=5\left(x^2-2\right)+18$
- результат "открытия скобок слева" оставим пока в скобках $11x-\left(18x+6-6x^2-2x\right)=5x^2-10+18$ ,
- приведем подобные в скобке, откроем; справа упростим $11x-16x-6+6x^2=5x^2+8$, перенесем слагаемые $-5x-6+6x^2-5x^2-8=0$,
- приведем подобные $x^2-5x-14=0$ , по формулам $x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{-5+\sqrt{81}}{2\cdot1}=\frac{-5+9}{2}=2$ ; и $x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}==\frac{-5-9}{2}=-7$ ; Ответ: $x_1=2$ ; $x_1=-7$.
Пример 13: Решить уравнение $-0,3x^2+0,8x-1,7=0$
- Как избавиться от коэффициентов - десятичные числа,? Обе части домножим на десятку (или 100 ...). Запятые уйдут.
- получим $-10\left(-0,3x^2+0,8x-1,7\right)=\left(-10\right)\cdot0$ $\Leftrightarrow$ $3x^2-8x+17=0$ . далее, по формулам ...
Пример 14: Решить уравнение $\frac{3}{4}x^2-\frac{5}{6}x-\frac{7}{3}=0$
- Тут дробные коэффициенты. Умножить обе части уравнения на кратное всех знаменателей: на $12$ (делится на каждое $4$, $6$, $3$ ).
- Дроби исчезнут! получим $12\cdot\left(\frac{3}{4}x^2-\frac{5}{6}x-\frac{7}{3}\right)=12\cdot0$ $\Leftrightarrow$ $9x^2-10x-14=0$. Далее, по формулам .....
Уравнения типа " произведение = 0 ", распад
Пример 16: Решить уравнение $(x+4)\cdot\left(5-3x\right)=0$
- Произведение $(x+4)\cdot\left(5-3x\right)$ равно 0 лишь тогда, когда какая-либо скобка станет 0, "обнулится".
- $x+4=0$ $\Rightarrow$ $x=-4$ . $5-3x=0$ $\Rightarrow$ $x=\frac{5}{3}$
- При х - числах $x=-4$ и $x=\frac{5}{3}$ произведение $(x+4)\cdot\left(5-3x\right)$ становится нулём! ответ: $x=-4$ $x=\frac{5}{3}$
Пример 17: Решить уравнение $(8-x)\cdot\left(2x+7\right)=0$
- Опорный факт: Если произведение $A\cdot B \cdot C$ = $0$ тогда либо $A$, либо $B$, либо $C$ = $0$
- Правило: уравнение " произведение = $0$ " разбивается на случаи: каждый множитель = $0$
- Разбиение на 2 случая: приравняем содержимое каждой скобки к нулю. и, решаем каждое уравнение по отдельности.
- случай 1 $2x+7=0$ $\Leftrightarrow$ $2x=-7$ $\Leftrightarrow$ $x=-3.5$
- случай 2 $8-x=0$ $\Leftrightarrow$ $x=8$ ответ: $x_1=8$ $x_2=-3.5$
Способ разбиения уравнения, разложения на множители:
- шаг 1: Обнулить правую часть уравнения, перенести все слагаемые влево. "левая часть = $0$".
- шаг 2: Разложить, вынести множители за скобки, превратить левую часть в произведение. " = $0$".
- шаг 3, 4 ... : Рассмотреть случаи: для каждого составить уравнения "множитель = $0$".
- далее: Решать получившиеся более мелкие уравнения. ответ: собрать все полученные решения..
Решение неполных квадратных уравнений: разложение, вынесение за скобку
Уравнение вида $ax^2+bx=0$: решается вынесением общего множителя $x$ за скобку. После вынесения уравнение $x\cdot\left(ax+b\right)=0$ распадается на два уравнения, 2 случаи.
Уравнение вида $ax^2=cx$: решается переносом $cx$ влево и вынесением общего множителя. После приведения к виду $ax^2-cx=0$ выносим множитель $x$ за скобки и решаем 2 случая.
Пример 18: Решить уравнение $6x^2–2x=0$ ;
- вынесем общий множитель за скобки: $2x\cdot(3x – 1)=0$ ; распад на два случая:
- $2x=0$ $\Rightarrow$ $x=0$ ; $3x–1=0$ $\Rightarrow$ $x=\frac{1}{3}$ . ответ: соберем все решения: $x_1=0$ ; $x_2=\frac{1}{3}$
Пример 19: Решить уравнение $50x^2-7x=0$
- вынесем общий $x\cdot\left(50x-7\right)=0$. 1-й: $x=0$ ; 2-й: $50x-7=0$ ... $x=\frac{7}{50}$
Пример 20: Решить уравнение $4x^2=10x$
- Через сокращение $x$ решать это уравнение нельзя, т.к. потеряется корень $x=0$. Правильное решение - перенести всё в одну часть, затем вынести неизвестное за скобку
Уравнение вида $(ax)^2=c^2$: решается применением формули разности квадратОВ. После переноса и разложения по формуле приведится к виду $(ax-c)(ax+c)=0$ . Далее решаем 2 случая.
Пример 21: Решить уравнение $9x^2-16=0$
- Разложим $9x^2-16$ на множители по формуле "разность квадратОВ": $(3x-4)\cdot\left(3x+4\right)=0$
- Произведение двух скобок равно нулю. два случая - $3x-4=0$ $\Rightarrow$ $3x=4$ . $3x+4=0$ $\Rightarrow$ $3x=-4$
Пример 22: Решить уравнение $(3-x)\cdot\left(4x+6x^2\right)\cdot\left(x^2-1\right)=0$
- Произведение скобок равно нулю. Для каждого множителя напишем уравнение "обнуления": Каждое "скобка = 0" и решим каждое.
- №1 $x^2-1=0$ $\Rightarrow$ $(x-1)(x+1)=0$ $x-1=0$ $x+1=0$ $x=-1$ $x=1$
- №2 $4x+6x^2=0$ $\Rightarrow$ $2x(2x+3)=0$ $x=0$ $2x+3=0$ $x=-\frac{3}{2}$
- №3 $3-x=0$ $\Rightarrow$ $x=3$ ответ: $x=3$ $x=0$ $x=-1,5$ $x=-1$ $x=1$
Дробно-рациональные уравнения
ОДЗ - множество значений неизвестного, при которых имеют смысл все входящие выражения.
- Уравнения $\frac{x-2}{x+3}=0$ , $5y=\frac{2+4y}{3y-7}+14$ , $\frac{6x+5y}{11xy}=\frac{xy}{2x+12y}$ теряют смысл, если знаменатель станет нулем.
- ОДЗ означает "мы пока не знаем какие числа могут уравнять, но мы точно знаем какие не могут:
- перечисляем условия ОДЗ, чтобы не пропустить ложные числа. Отфильтровать плохие, недопустимые числа."
Пример 23 Решить уравнение $\frac{3-2x}{x+2}=\frac{30}{5-x}$
- ОДЗ $x+2\ne0$ $5-x\ne0$ (суть написания ОДЗ - не допустить ложные решения: решением уравнения
- могут быть только те числа, будучи подставлеными в обе части уравнения вместо неизвестного $x$, уравняют обе части.)
- 1-ый шаг. дробь равна дроби. свойство пропорции: если $\frac{A}{B}=\frac{C}{D}$ , тогда $A\cdot D=C\cdot B$. значит, чтобы
- найти $x$ , уравнивающий эти дроби, достаточно найти решения уравнения $\left(3-2x\right)\left(5-x\right)=30\cdot\left(x+2\right)$ ,
- 2-ой шаг. раскрыв скобки, перейти к решению квадратного уравнения $15-3x-10x+2x^2=30x+60$
- $\Leftrightarrow$ $2x^2-43x-45=0$ $\Leftrightarrow$ решения уравнения : $x_1=22,5$; $x_2=-1$ .
- осталось проверить ОДЗ условия $\Rightarrow$ оба числа принадлежат ОДЗ, значит это корни уравнения.
Алгоритм решения уравнения "дробь = дробь"
$\frac{A\left(x\right)}{B\left(x\right)}=\frac{C\left(x\right)}{D\left(x\right)}$ решается переходом к квадратному по свойству пропорций $\Rightarrow$ $A\left(x\right)\cdot D\left(x\right)=C\left(x\right)\cdot B\left(x\right)$ .
$1)$: $\frac{x^2-3x}{7-2x}=\frac{x+1}{5}$ $\Rightarrow$ $\left(x^2-3x\right)\cdot5=\left(x+1\right)\cdot\left(7-2x\right)$ .
$2)$: $\frac{x^2-17}{5-x}=-1$ $\Rightarrow$ $x^2-17=-1\cdot\left(5-x\right)$

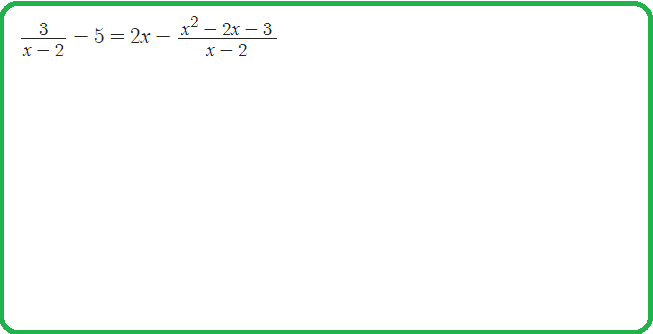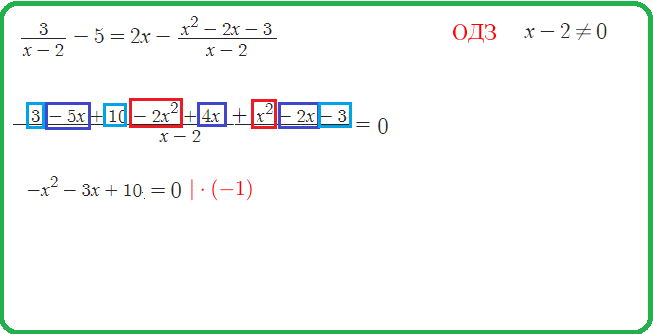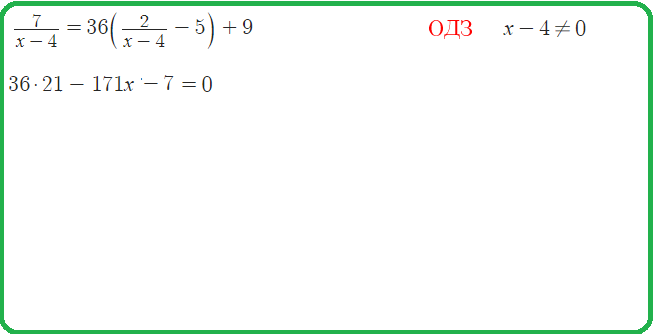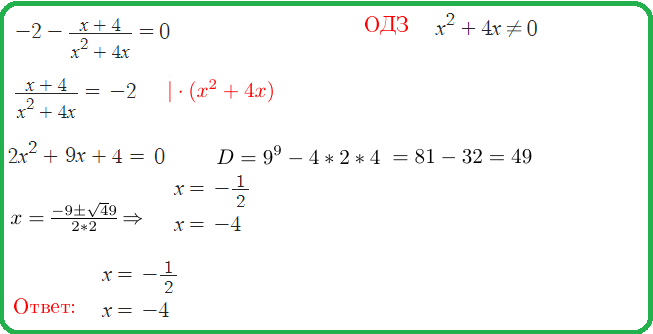
Пример 24: Решить уравнение $\frac{x^2-5x+6}{x^2-9}=0$
- ОДЗ $x^2-9\ne0$ ( знаменатель не может быть равен $0$ , значит $x$ не может быть равен $+3$ и $-3$ .)
- в нашем уравнении " дробь = ноль " $\Leftrightarrow$ простое рассуждение: вся дробь равна нулю значит, числитель
- равен нулю. как иначе дробь обнулится? Никак! $x^2-5x+6=0$ $\Leftrightarrow$ $D=5^2-4\cdot1\cdot6 = 1$ получаем
- $x_1=2$ $x_2=3$ , проверим истинность решений: $x=3$ оно не удовлетворяет условию ОДЗ , значит,
- это ложный корень. ответ: $x=2$
Алгоритм решения уравнения "дробь = 0" :
$\frac{A\left(x\right)}{B\left(x\right)}=0$ эквивалентно $\Leftrightarrow$ $A\left(x\right)=0$ $B\left(x\right)\ne0$ . числитель $= 0$, знаменатель $\ne0$.
Пример 25: Решить уравнение $\frac{x^2-7}{x-3}=\frac{2}{x-3}+12$
- ОДЗ $x-3\ne0$
- приведем к общему знаменателю $\frac{x^2-7}{x-3}=\frac{2}{x-3}+\frac{12\left(x-3\right)}{x-3}$ , сложим числители справа $\frac{x^2-7}{x-3}=\frac{2+12\left(x-3\right)}{x-3}$,
- избавимся от дробей путем домножения обеих частей уравнения на общий знаменатель $x^2-7=2+12\left(x-3\right)$ ,
- перенесем в левую часть и получим желаемое уравнение $x^2-12x+27=0$ $\Leftrightarrow$ $x_1=3$ ; $x_2=9$ .
- проверим: принадлежат ли корни ОДЗ уравнения ( $x-3\ne0$ ) ? . корень $x=3$ не удовлетворяет ОДЗ ,
- за это его исключают из множества решений. такие корни называют посторонними, ложными корнями.
- ответ: $x=9$
Алгоритм решения дробно-рациональных уравнений:
- I. определить условия ОДЗ уравнения. какие выражения не могут быть нулем?
- II. привести все слагаемые в обеих частях уравнения к общему знаменателю.
- III. домножить обе части уравнения на общий знаменатель. сократить.
- IV. найти и корни, решения полученного уравнения.
- V. проверить, принадлежат ли найденные корни ОДЗ.
- VI. записать в ответе те из найденных корней, которые принадлежат ОДЗ.
Пример 26: Решить уравнение $\frac{2x+4}{2x-1}-3=\frac{15-6x}{2x-3}$
- ОДЗ $2x-1\ne0$ $2x-3\ne0$
- превратим числовое слагаемое в дробь $\frac{2x+4}{2x-1}-\frac{3}{1}=\frac{15-6x}{2x-3}$ и применим правило сложения алгебраических дробей
- $\frac{A}{B}\pm\frac{C}{D}=\frac{A\cdot D\pm C\cdot B}{B\cdot D}$ : $\frac{2x+4-3\cdot\left(2x-1\right)}{2x-1}=\frac{15-6x}{2x-3}$ , упростим $\frac{-4x+7}{2x-1}=\frac{15-6x}{2x-3}$ , перенесем правую дробь
- к левой дроби $\frac{-4x+7}{2x-1}-\frac{15-6x}{2x-3}=0$ и выполним сложение дробей с общим знаменателем , равным
- произведению двух множителей $\frac{\left(-4x+7\right)\left(2x-3\right)-\left(15-6x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-3\right)}=0$ если "дробь = $0$ " тогда
- "числитель = $0$ получим $\left(-4x+7\right)\left(2x-3\right)-\left(15-6x\right)\left(2x-1\right)=0$ , раскроем скобки
- $-8x^2+12x+14x-21-30x+15+12x^2-6x=0$ , приведем к стандартному виду $4x^2-10x-6=0$
- и сократим на $2$: $\Rightarrow$ $2x^2-5x-3=0$ . ответ: $x_1=3$ $x_2=-\frac{1}{2}$ . ОДЗ выполняется для обеих корней.
Алгоритм решения уравнения "дробно - рациональное выражение = дробь":
- решается превращением суммы дробей в одну дробь по правилу сложения дробей $\frac{A}{B}\pm\frac{C}{D}=\frac{A\cdot D\pm C\cdot B}{B\cdot D}$.
- Если дробь складывается с каким-то числом $К$ , его предварительно заменяют $\frac{K}{1}$ - дробью со знаменателем $1$ .
- полученное "дробь = дробь" преобразуют в "дробь = 0" . затем переход к уравнению "числитель = 0".
- проверка корней на соответсвие условиям ОДЗ обязательна.


Свойства Степеней:
$a^m\cdot a^n=a^{m+n}$ $a^{x+y}=a^x\cdot a^y$ ; $\frac{a^m}{a^n}=a^{m-n}$ $a^{x-y}=\frac{a^x}{a^y}$
$\left(a^x\right)^y=a^{xy}$ $a^{mn}=\left(a^m\right)^n$ $\left(a\cdot b\right)^x=a^x\cdot b^x$ $a^n\cdot b^n=\left(a\cdot b\right)^n$
$\left(\frac{a}{b}\right)^x=\frac{a^x}{b^x}$ $\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n$ $a^{\frac{x}{y}}=\left(\sqrt[y]{a}\right)^x$ ; $\sqrt[m]{a^n}=a^{\frac{n}{m}}$
$a^{-x}=\frac{1}{a^x}$ ; $\left(\frac{a}{b}\right)^{-x}=\left(\frac{b}{a}\right)^x$
Свойства Логарифмов:
Основное тождество $\log_ab=n$ $\Leftrightarrow$ $b=a^n$ $a^{\log b_a}=b$
сумма логарифмов $\log_ax+\log_ay=\log_axy$ разность логарифмов $\log_ax-\log_ay=\log_a\frac{x}{y}$
вынос показателя $\log_a\left(b^c\right)=c\cdot\log_ab$ внесение под знак логарифма $c\cdot\log_ab=\log_a\left(b^c\right)$
обратное логарифма $\log_ab=\frac{1}{\log_ba}$ формула замены основания: $\frac{1}{\log_ba}=\log_ab$
Решение простейшего уравнения: $\log_af\left(x\right)=c$ $\Rightarrow$ $f\left(x\right)=a^c$ $\log_af\left(x\right)=\log_ag\left(x\right)$ $\Rightarrow$ $f\left(x\right)=g\left(x\right)$
Показательные уравнения
Показательная функция имеет вид $a^{f\left(x\right)}$ . основание - числовое выражение, показатель - выражение с переменным.
Простейшее показательное уравнение имеет вид $a^{f\left(x\right)}=a^n$ , сводится к равенству показателей $f\left(x\right)=n$ при одинаковых основаниях.
Формулы, свойства степеней:
- Умножение степеней - основание одинаковые, показатели складываются: $a^m\cdot a^n=a^{m+n}$ $\Leftrightarrow$ $a^{x+y}=a^x\cdot a^y$ ;
- $\frac{a^m}{a^n}=a^{m-n}$ $\Leftrightarrow$ $a^{x-y}=\frac{a^x}{a^y}$ Делении степеней с одинаковыми основаниями - основание прежнее, показатели вычитаются.
- $\left(a^x\right)^y=a^{xy}$ $\Leftrightarrow$ $a^{mn}=\left(a^m\right)^n$ Возведении степени в степень показатели перемножаются. И наоборот!
- $\left(a\cdot b\right)^x=a^x\cdot b^x$ $\Leftrightarrow$ $a^n\cdot b^n=\left(a\cdot b\right)^n$ Возведение в степень произведения - в эту степень возводится каждый множитель:
- $\left(\frac{a}{b}\right)^x=\frac{a^x}{b^x}$ $\Leftrightarrow$ $\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n$ Возведение в степень дроби в эту степень возводится числитель дроби и знаменатель . Деление?
- Дробная степень: $a^{\frac{x}{y}}=\left(\sqrt[y]{a}\right)^x$ ; $\sqrt[m]{a^n}=a^{\frac{n}{m}}$ Знаменатель как корень. Числитель как степень.
- Отрицательная степень $\Leftrightarrow$ обратная степень : $a^{-x}=\frac{1}{a^x}$ ; $\left(\frac{a}{b}\right)^{-x}=\left(\frac{b}{a}\right)^x$
Пример 31: Решить уравнение $8^{3-x}=4$
- числа $8$ и $4$ можно представить как степени с основанием $2$ : $\left(2^3\right)^{3-x}=2^2$ . по формуле степень в степени
- $2^{3\cdot\left(3-x\right)}=2^2$ - получили простейшее показательное уравнение с одинаковыми основаниями слева и справа $\Rightarrow $
- приравняем показатели $3\cdot\left(3-x\right)=2$ , решим $9-3x=2$ $\Leftrightarrow$ $3x=7$ $\Leftrightarrow$ $x=\frac{7}{3}$ .
- ответ: $x=\frac{7}{3}$
Пример 32: Решить уравнение $5^{-3x+1}=0.2^{\frac{1}{3}}\cdot\sqrt{125}$
- Преобразуем уравнение к простейшему виду : $5$ в степени какое - то выражение = $5$ в степени число .
- Заметим , $0,2$ и $125$ являются степенями $5$ : $5^{-3x+1}=\left(\frac{1}{5}\right)^{\frac{1}{3}}\cdot\sqrt{5^3}$ $\Leftrightarrow$ $5^{-3x+1}=5^{-\frac{1}{3}}\cdot5^{\frac{3}{2}}$ ,
- используем свойства степеней : $5^{-3x+1}=5^{-\frac{1}{3}+\frac{3}{2}}$ $\Leftrightarrow$ $5^{-3x+1}=5^{\frac{7}{6}}$ $\Leftrightarrow$ и приходим к нашей цели -
- к простейшему уравнению , приравняем показатели: $-3x+1=\frac{7}{6}$ $\Leftrightarrow$ $x=-\frac{1}{18}$ . ответ: $x=-\frac{1}{18}$
Пример 33: Решить уравнение $5^{x^2-1}=3^{x^2-1}$
- нам задано равенство двух показательных функций при одинаковых показателях , но разных основаниях.
- когда сможет выполниться такое равенство? каким должен быть показатель, чтобы степени с разными основаниями
- $5$ и $3$ сравнялись . конечно, только при показателе $0$ , когда обе части будут просто единицами $1=1$ .
- добьемся этого преобразованиями: перенесем правую часть влево как делитель $\frac{5^{x^2-1}}{3^{x^2-1}}=1$
- по формуле отношений степеней с равными показателями превратит в одну функцию $\left(\frac{5}{3}\right)^{x^2-1}=1$ ,
- перепишем правую единицу как нулевую степень подходящего выражения $\left(\frac{5}{3}\right)^{x^2-1}=\left(\frac{5}{3}\right)^0$ $\Leftrightarrow$
- получим вид простейшего, сравняем показатели $x^2-1=0$ ответ: $x=1$ , $x=-1$ .
проб  проб
проб 
Логарифмические уравнения
Формулы, свойства логарифмов
- Основное тождество $\log_ab=n$ $\Leftrightarrow$ $b=a^n$ $a^{\log b_a}=b$ Логарифм есть показатель степени.
- сумма логарифмов $\log_ax+\log_ay=\log_axy$ логарифм произведения. разность логарифмов $\log_ax-\log_ay=\log_a\frac{x}{y}$
- формула замены основания: $\log_ab=\frac{1}{\log_ba}$ обратное логарифма $\frac{1}{\log_ba}=\log_ab$
- Вынос показателя степени аргумента: $\log_a\left(b^c\right)=c\cdot\log_ab$ ; и наоборот: множитель заносится внутрь $c\cdot\log_ab=\log_a\left(b^c\right)$
- Вынос показателя степени основания: $\log_{\left(a^n\right)}b=\frac{1}{n}\cdot\log_ab$ ; множитель заносится как корень основания $n\cdot\log_ab=\log_{\left(a^{\frac{1}{n}}\right)}b$
- Переход к новому основанию: $\log_ab=\frac{\log_xb}{\log_xa}$ ; отношение двух логарифмов с одинаковым основанием $\frac{\log_xb}{\log_xa}=\log_ab$
- Перекрестное произведение логарифмов: $\log_ax\cdot\log_xb=\log_ab$ ; аргумент одного равен основанию другого, как будто "сокращение" .
- Универсальная формула для степеней внутри логарифма: $\log_{\left(a^n\right)}\left(b^m\right)=\frac{m}{n}\cdot\log_ab$ ;
- Транзит, логарифм в показателе: $a^{\log_xb}=b^{\log_xa}$ $2^{\log_83}=3^{\log_82}$
Решение простейшего: $\log_af\left(x\right)=c$ $\Rightarrow$ $f\left(x\right)=a^c$ $\log_af\left(x\right)=\log_ag\left(x\right)$ $\Rightarrow$ $f\left(x\right)=g\left(x\right)$
- По основному тождеству: аргумент логарифма равен основанию в степени правая часть. "вскрыть логарифм".
- При равенстве двух логарифмов с одним и тем же основанием, приравниваем аргументы этих логарифмов.
- Все что нужно уметь для решения простейшего логарифмического уравнения - это знать "что такое логарифм".
Пример 34: Решить уравнение $\log_{49}\left(2x-1\right)=0.5$
- Какими решения не могут быть в принципе? нужно указать Область Допустимых Значений:
- О.Д.З. $2x-1 > 0$ ограничение: недопустимо чтобы под логарифмом оказалось неположительная величина.
- "вскроем логарифм" по основному тождеству: аргумент уравняется с "основанием в степени правое число",
- $\log_af\left(x\right)=c$ $\Rightarrow$ $f\left(x\right)=a^c$ в нашем случае $a=49$ $f\left(x\right)=2x-1$ $c=0.5$ получаем
- $2x-1=49^{0.5}$ $\Rightarrow$ $2x=7+1$ $\Rightarrow$ $x=4$ проверка О.Д.З. , удовлетворяет. Ответ: $x=4$


Пример 35: Решить уравнение $\log_{\frac{1}{3}}x-\log_{\frac{1}{3}}36=\log_{\frac{1}{3}}10$ О.Д.З. $x > 0$
- Здесь два логарифма. для превращения в простейшее уравнение, превратим два логарифма в один по формуле
- разности логарифмов: $\log_ax-\log_ay=\log_a\frac{x}{y}$ здесь $a=\frac{1}{3}$ $x=x$ $y=36$ . тогда получим
- $\log_{\frac{1}{3}}\frac{x}{36}=\log_{\frac{1}{3}}10$ решаем как простейшее $\frac{x}{36}=\left(\frac{1}{3}\right)^{\log_{\frac{1}{3}}10}$ получаем $\frac{x}{36}=10$ проверим О.Д.З.,
- Ответ: $x=360$
- можно было: перенести числовой логарифм вправо $\log_{\frac{1}{3}}x=\log_{\frac{1}{3}}36+\log_{\frac{1}{3}}10$ упростить по формуле
- $\log_{\frac{1}{3}}x=\log_{\frac{1}{3}}\left(36\cdot10\right)$ и так далее .....
Пример 36: Решить уравнение $\log_{0.6}\left(2x^2-3x+1\right)=\log_{0.6}\left(13-x\right)$
- О.Д.З. $2x^2-3x+1 > 0$ $13 > x$ комментарий: 2 логарифма, 2 условия ОДЗ. в конце нужно проверить оба.
- два логарифма с одинаковыми основаниями равны? значит, по основному тождеству можно приравнять
- аргументы. $2x^2-3x+1=13-x$ , перенесем все в левую часть $2x^2-2x-12=0$ , разделим на $2$
- $x^2-x-6=0$ решим уравнение. проверим ОДЗ ..... Ответ: $x_1=-2$ ; $x_2=3$
Алгоритм:
-
Написать ограничения ОДЗ: условия верности - допустимости возможных решений
-
По возможности уменьшать количество логарифмов - использовать преобразования для сведения к одному логарифму.
-
Эквивалентными преобразованиями свести уравнение к простейщему виду: логарифм равен числу, или логарифму.
-
"Вскрыть" простейщее логарифмическое уравнение, перейти к не - логарифмическому, более простому и решить.
-
Полученные корни - решения проверить на выполнение ОДЗ, ограничений: проверка ложности кандидата.
Иррациональные уравнения
Правило возведения в квадрат обеих частей уравнения::
если $A=B$ , тогда $A^2=B^2$ , но не наоборот: ($A^2=B^2$ не $\Leftrightarrow$ $A=B$ ) .
$A^2=B^2$ $\Rightarrow $ $A=B$ при условии: $A$ и $B$ одного и того же знака.
$\sqrt{X}=C$ $\Rightarrow $ $X=C^2$ при условии: $C\ge0$ , $C$ - неотрицательна.
Простейшие уравнения с радикалами
Пример 41: Решить уравнение $\sqrt{\frac{3+12x}{2x-1}}=3$
- Вопрос к уравнению: каким числом должно быть неизвестное $x$ , чтобы стать корнем уравнения ,
- т.е. чтобы уравнять собой левую и правую части ? не знаем каким числом в будущем окажется $x$ ,
- но сейчас , очевидно , дробь $\frac{3+12x}{2x-1}$ должна равняться $9$ . а как иначе левое станет $3$? никак.
- вывод: чтобы сравнялись части, нужно, чтобы сравнялись их квадраты . $A=B$ $\Rightarrow$ $A^2=B^2$ .
- метод решения - избавление от радикала - возведение обеих частей в квадрат: формула $\left(\sqrt{A}\right)^2=A$ - .
- применим этот метод и возведем обе части в квадрат $\left(\sqrt{\frac{3+12x}{2x-1}}\right)^2=\left(3\right)^2$ $\Leftrightarrow$ - так избавимся от радикала
- $\frac{3+12x}{2x-1}=9$ и получим "простое" без радикалов уравнение $3+12x=9\cdot\left(2x-1\right)$ $\Leftrightarrow$ $12=18x-12x$ ,
- наконец-то найдем то самое число , каким должно быть неизвестное ответ: $x=2$
Пример 42: Решить уравнение $\sqrt{6-4x-x^2}=-3-2x$
- В начале уточним некоторые детали. не знаем каким станет выравнивающий обе части $x$ , но в любом случае:
- под радикалом должно быть неотрицательное значение. иначе получится "ложь" - бессмыслица.
- надо указать ОДЗ - ограничение $6-4x-x^2\ge0$ : (допустимо!) все, что под радикалом $\ge0$.
- избавимся от радикала одновременным возведением обеих частей в квадрат.
- но это не гарантирует "уравнивания до возведения" . (Может было 4 = -4 , стало 16 = 16)
- бывает такое: после возведения в квадрат части уравниваются, хотя до операции они были не равны .
- например: $\left(-3\right)^2=\left(3\right)^2$ , но ведь $-3\ne3$ .
- нам нужны гарантии , что равные после возведения в квадрат части $A^2=B^2$ , были бы равными и до
- такое возможно только при условии : обе части уравнения до возведения $A$ и $B$ должны быть одного знака.
- $\left(\sqrt{6-4x-x^2}\right)^2=\left(-3-2x\right)^2$ при условии $-3-2x\ge0$ (правая часть до возведения должна быть $\ge0$ )
- оговорка при условии гарантирует одинаковость знаков частей "до" операции возведения в квадрат :
- левая часть - это радикал , он неотрицателен $\Rightarrow$ значит правая часть уравнения неотрицательна.
- используем формулы: $\left(\sqrt{a}\right)^2=a$ ; $\left(a+b\right)^2=a^2+2ab+b^2$ получим $6-4x-x^2=9+12x+4x^2$
- решим квадратное уравнение $5x^2+16x+3=0$. два корня $x=-3$ , $x=-0.2$ .
- внимание: корни должны пройти ОДЗ и при условии. Если какой-то не проходят, значит этот корень ложный.
- проверка: $x=-3$ 1) ОДЗ - да!. 2) "при" $-3-2x\ge0$ - да! $\Rightarrow$ истинное решение.
- проверка: $x=-0.2$ $\Rightarrow$ 1) ОДЗ - да!. 2) "при" $-3-2x\ge0$ - нет! $\Rightarrow$ ложное решение.
- ответ: $x=-3$ в ответе перечисляем только истинные, уравнивающие решения.
Область Допустимых Значений - ОДЗ - ОДЗ выражения, ОДЗ уравнения
- те числовые значения переменной, при которых выражения имеют смысл ... вычисляются.
- но не те числа, при которых выражение невозможно вычислить
- ОДЗ уравнения - те числовые значения неизвестного, при которых выполняется ОДЗ каждого выражения.
- У выражения с квадратным радикалом ОДЗ условие: под радикальное выражение неотрицательно.
- Если в уравнении есть радикалы, то условия ОДЗ: Каждое подрадикальное $\ge0$. (под корнем минусовое нельзя)
- Если есть дробь, то условия ОДЗ: каждый знаменатель $\ne0$. (делить на 0 нельзя!)
Один радикал в уравнении
Напоминание: Избавиться от радикала в уравнении $\sqrt{A}=B$ можно путем возведения его в квадрат $\left(\sqrt{ }\right)^2$ , для этого радикал должен быть уединенным в одной из частей уравнения $\sqrt{A}$. "При условии" относится к противоположной от радикала части уравнения - выражению $B$ и накладывается до возведения в квадрат, но пишется при возведении $\left(B\right)^2$
Пример 43: Решить уравнение $\sqrt{5-x^2}-2x=3-x$
- вопросы: как нам из этого уравнения получить такое, какое мы уже научились решать? как нам прийти к виду "радикал равняется не радикальному выражению" ?
- NB: "правильно поставленный вопрос уже полдела. все открытия начинаются от хорошего вопроса. ставьте вопросы! "
- ОДЗ $5-x^2\ge0$ $\Leftrightarrow $ условие ОДЗ гарантирует "не ложность" решения. перенесем все нерадикальные
- слагаемые на противоположную от радикала сторону $ \sqrt{5-x^2}=2x+3-x$ - так мы уединяем радикал.
- возведение обеих частей в квадрат и "при условии" : $\left(\sqrt{5-x^2}\right)^2=\left(x+3\right)^2$ при $x+3\ge0$
- далее, $5-x^2=x^2+6x+9$ $\Leftrightarrow$ $2x^2+6x+4=0$ $\Leftrightarrow$ $x^2+3x+2=0$ $\Rightarrow$ корни $x=-1$ , $x=-2$
- ответ: $x=-1$ , $x=-2$ оба корня истинные, т.к. проходят ОДЗ и "при условии".
Равенство радикалов
Пример 44: Решить уравнение $\sqrt{2-x+x^2}-\sqrt{6-2x}=0$
- ОДЗ: $2-x+x^2\ge0$ ; $6-2x\ge0$ - условие допустимости к решению : определяем когда радикалы существуют.
- перенесем один из радикалов направо, тем самым сравняем радикалы и подготовим возведение в квадрат обеих частей,
- $\sqrt{2-x+x^2}=\sqrt{6-2x}$ . "при условии" писать не будем , ведь обе части уже $\ge0$ из-за радикалов, см. ОДЗ.
- $\Leftrightarrow$ $2-x+x^2=6-2x$ $\Leftrightarrow$ $x^2+x-4=0$ $\Leftrightarrow$ $x=\frac{-1-\sqrt{17}}{2}$ $x=\frac{-1+\sqrt{17}}{2}$ . бракуем ложные?
дальнейшая стратегия:
I. избавимся от радикалов: возведем обе части в квадрат. условия не нужны, радикалы одного знака. II. решим полученное нерадикальное уравнение. III. Проверим решения на выполнимость всех ОДЗ ограничений. забракуем ложные корни.
В пустых ЛИСТах #71 - #74 можно интерактивно решать любые уравнения, хоть из сайта сдам.егэ:
Уравнения, Задачи из Задания №1, ЕГЭ - профиль