
Смежные и вертикальные углы
- Урок здесь, XIII . §4. Вертикальные и Смежные Углы.
Пара углов с общей вершиной может быть смежными или вертикальными, если у них общая вершина, а стороны ... ??
Смежные углы имеют общую вершину, одну общую сторону, а другие стороны являются продолжениями друг друга.
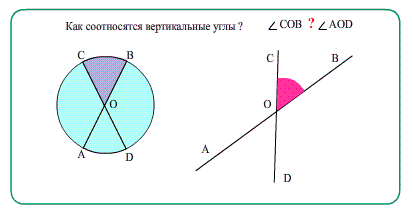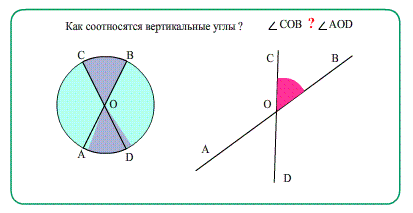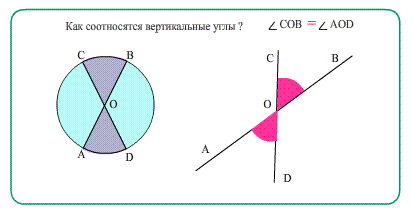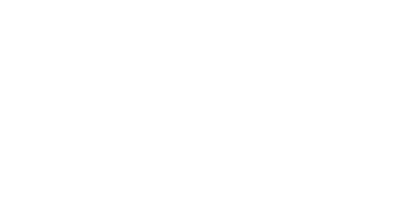
Вертикальные углы имеют общую вершину, а каждая сторона одного угла является продолжением стороны второго угла.
Теорема Сумма смежных углов равна развернутому углу – 180 градусов.
Теорема Вертикальные углы равны. При наложении такие углы полностью совпадут, совместятся.
Интерактивные Упражнения: Решить задачи №11 - №14
Углы при Параллельных
- Урок здесь, XIII . §6. Углы при Двух Параллельных и Секущей
пара накрест лежащие углы : ∠3 и ∠5, ∠4 и ∠6;
пара односторонние углы : ∠4 и ∠5, ∠3 и ∠6;
пара соответственные углы : ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.
Свойства:
- накрест лежащие углы равны: 3 = 5, 4 = 6.
- соответственные углы равны: 1 = 5, 4 = 8, 2 = 6, 3 = 7.
- сумма односторонних углов равна 180 градусов: 3 + 6 = 180 градусов, 4 + 5 = 180 градусов.

Факты, Следствия из теорем о углах при параллельных и секущей к ним:
- В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы. Что секущая?
- В паралеллограмме сумма углов у одной стороны равен 180 град. - внутренные односторонные. Что секущая?
- В трапеции сумма углов у боковых сторон равен 180 град. - внутренные односторонные. Что секущая?
- Еще о углах: Диаметры в окружности при пересечении образуют равные вертикальные углы.
- Сумма углов треугольника 180 градусов . Достроить параллельную, увидеть секущую!
Интерактивные Упражнения: Решить задачи №15 - №19
Ромб - это параллелограмм, у которого все стороны равны.
-
Урок здесь, XIII . §12. Ромб: симметрии, свойства. Квадрат
-
"Чтоб Выучить, распознать нечто неподвижное - узнать его в движении, при изменениях" Ромб провернем на 180 градусов вокруг точки пересечения диагоналей - ромб совместится с самим собой. Симметрия. Отразим ромб зеркально по диагонали - новый ромб совпадет с прежним. Симметрия. Отразим ромб зеркально по другой диагонали - ромб совпадает с самим собой. Симметрия. Замечание: Если "зряче видим" центральную и осевые симметрии ромба, то все его свойства у нас "в кармане".
Свойства ромба:
- Ромб симметричен относительно точки O - пересечения диагоналей. O - центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ - ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $\angle A=\angle C$ , $\angle B=\angle D$ . Прилежащие $\angle A+\angle B=180^o$ , $\angle A+\angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=\frac{AC}{2}$ и $BO=OD=\frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $\bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $\bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов - делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
Интерактивные Упражнения: Решить задачи №21 - №27
Трапеция
Факты, Свойства и Формулы трапеции:
- Параллельные стороны называются основаниями, $BC \parallel AD$ . Другие две - боковыми сторонами.
- Сумма односторонных углов при боковой стороне равна $180^{\circ}$ : $\angle 1 + \angle 2 = 180^{\circ}$ , $\angle 3 + \angle 4 = 180^{\circ}$.
- Диагональ является секущей к паралелльным основаниям $\Rightarrow$ равные накрест лежащие углы: $\angle BCA=\angle CAD$.
- При пересечении диагоналей (т. $O$) образуются вертикальные углы $\angle BOC=\angle AOD$ и смежные $\angle AOB+\angle BOC=180^{\circ}$.
- Средняя линия трапеции (отрезок, соединяющий середины боковых) параллельна основаниям и равна их полусумме $\frac{a+b}{2}$ .
- Высоты на основания $BH$ , $CK$ равны и делят основание на части $AD=AH+HK+KD$ , причем $HK=BC$ .
Равнобедренная трапеция - трапеция с равными боковыми сторонами, $AB=CD$ - "бедра" равны .
- Свойства и формулы у равнобедренной трапеции те же самые, что и у простой трапеции плюс:
- Углы у оснований равны $\angle A = \angle D$ , $\angle C = \angle B$ .
- Высоты отсекают от основания равные отрезки $AH=KD=\frac{a-b}{2}$ - полуразность оснований.
- Диагонали одинаково наклонены к основаниям $\angle CAD=\angle BDA=\angle DBC=\angle ACB$ и
образуют подобные равнобедренные треугольники. - Диагонали образуют "верхные" и "нижные" подобные равнобедренные треугольники. $\bigtriangleup BOC$ и $\bigtriangleup AOD$
- Диагонали образуют равные "левые" и "правые" треугольники : $\bigtriangleup ABD$ и $\bigtriangleup ACD$ ; $\bigtriangleup ABC$ и $\bigtriangleup BCD$.
Интерактивные Упражнения: Решить задачи №31 - №35
Формулы площадей фигур
Площадь фигур, свойство аддитивности
Площадь - это численная характеристика геометрической фигуры, показывающая размер этой фигуры:
1) Единица площади: Площадь единичного квадрата $1$ х $1$ равна $1$.
2) Cвойство аддитивности: Площадь фигуры равна количеству покрывающих её равных квадратиков ,
- Сколько единичных квадратиков покроют фигуру, столько и есть площадь этой фигуры.
- Даже если какие-то квадратики пришлось "порезать" и пересобрать в другом порядке.
- Если фигура состоит из кусков с уже известными площадями 17 и 25, то площадь этой фигуры = 17 + 25 = 32.
Площадь фигуры величина положительная , её численное значение обладает следующими свойствами:
- равные фигуры имеют равные площади ;
- площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
- площадь квадрата, построенного на единичном отрезке, равна единице.
- Измеряется площадь в квадратных единицах ($см^2$ , $м^2$ ), как сумма элементарных квадратиков со стороной $1$ .
- Свойство аддитивности позволяет вычислять площадь не только по формуле суммы, но и по формуле разности.
- Можно достроить искомую фигуру до прямоугольника, найти площади всех получившихся дополнительных фигур и площадь самого прямоугольника.
- Площадь искомой фигуры равна Площадь прямоугольника минус Сумма площадей всех лишних фигур.
Площадь прямоугольника равна произведению ширины на высоту, т.е. произведению его сторон.:
- ширина показывает сколько квадратиков в каждой строке, а высота - сколько таких строк помещается.
- Перемножение количества строк на количество квадратиков в каждой полосе - это и есть произведение сторон прямоугольника.
- Осмыслите: для целых значений сторон нужно подсчитать покрытие всего прямоугольника единичными квадратиками.
- Осмысление даже при дробных значениях сторон ...... через умножение и деление ... т.е. "много одинаковых" ...
Теорема Площадь прямоугольника $S_{ABCD}=a\cdot b$ . Площадь равна произведению сторон (столько квадратиков покрывают прямоугольник) .
Теорема Площадь квадрата равна квадрату его стороны.
Теорема Площадь прямоугольного треугольника $S_{ABC}=\frac{a\cdot b}{2}$ - "половина произведения катетов" , "половина площади обрамляющего прямоугольника"
Теорема Площадь треугольника $S_{ABC}=\frac{a\cdot h}{2}$ - "половина произведения стороны и опущенного на эту сторону высота" , "половина площади обрамляющего прямоугольника"
Интерактивные Упражнения: Решить задачи №41 - №45
Тригонометрия прямоугольного треугольника
- Урок здесь, XIII . §22. Расчет прямоугольного треугольника.
Определение. В прямоугольном треугольнике тригонометрическими функциями острых углов называются числа:
- синусом угла называется отношение противолежащего катета к гипотенузе, $\sin\alpha=\frac{a}{c}$
- косинусом угла называется отношение прилежащего катета к гипотенузе, $\cos\alpha=\frac{b}{c}$
- тангенсом угла называется отношение противолежащего катета к прилежащему, $\tg\alpha=\frac{a}{b}$
- котангенсом угла называется отношение прилежащего катета к противолежащему, $\ctg\alpha=\frac{b}{a}$
- Замечание: Отношения сторон не зависят от длин катетов и гипотенузы, они зависят только от углов. Угол здесь очень важен. Не важно какие стороны в треугольнике длинные или короткие , важно их отношение - оно всегда одно и то же.
Формулы, соотношений в прямоугольном треугольнике, определения тригонометрических функций острых углов:
- $\sin A=\frac{BC}{AB}$ $\cos A=\frac{AC}{AB}$ $\tg A=\frac{BC}{AC}$ $\ctg A=\frac{AC}{BC}$
- $\cos B=\frac{AC}{AB}$ $\cos B=\frac{BC}{AB}$ $HC=AC\cdot\sin A$ $\frac{HC}{BC}=\frac{AC}{AB}$ $\angle$ACH=$\angle$B
- $S=\frac{a\cdot b}{2}$ $S=\frac{AB\cdot CH}{2}$ $HC=BC\cdot\sin B$ $\frac{HC}{AC}=\frac{BC}{AB}$ $\angle$BCH=$\angle$A
- Замечание: Катеты можно выразить через гипотенузу и синус (или косинус) острого угла и наоборот.
- Если в прямоугольном треугольнике известны две величины : две стороны или одна сторона и тригонометрия острого угла,
- все остальное можно вычислить - найти - расчитать по формулам.
Тождества: $\sin^2\alpha+\cos^2\alpha=1$ ; $\tg\alpha=\frac{\sin\alpha}{\cos\alpha}$ ; $\ctg\alpha=\frac{1}{\tg\alpha}=\frac{\sin\alpha}{\cos\alpha}$ .
Формула приведения тупых углов $90 < \alpha < 180$ к смежным острым углам $180-\alpha$ .
$\sin\left(\alpha\right)=\sin\left(180-\alpha\right)$ $\cos\left(\alpha\right)=-\cos\left(180-\alpha\right)$ , $\tg\left(\alpha\right)=-\tg\left(180-\alpha\right)$ , $\ctg\left(\alpha\right)=\ctg\left(180-\alpha\right)$ синус тупого угла такой же косинус, тангенс, котангенс тупого - со знаком "минус". как у "своего смежного" .
Факты:
- 1. Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту .
- 2. "О сумме острых углов": в прямоугольном треугольнике сумма острых углов равна 90 градусов.
- 3. "О $30^o$": в прямоугольном с углом $30^o$ катет напротив этого угла равен половине гипотенузы. Если к такому треугольнику приложить точно такой же получится равностронный с углами $60^o$ и катет напротив $30^o$ окажется ровно половиной стороны равностороннего ,а значит это катет $a=\frac{c}{2}$ ; другой катет легко получить по теореме Пифагора : $b=\frac{\sqrt{3}}{2}c$ .
- 4. "О $45^o$": прямоугольный $\bigtriangleup$ с острым углом в $45^o$ является равнобедренным ; его гипотенуза $c=\sqrt{2}$ * катет.
- 5. "О равнобедренном прямоугольном треугольнике": углы при основании равны и их сумма равна $90^o$ $\Rightarrow$ оба угла по $45^o$; катеты равны и по т. Пифагора $a^2+a^2=c^2$ $\Rightarrow$ оба катета $a=b=\frac{\sqrt{2}}{2}c$ и $c=\sqrt{2}a$ .
- 6. "О высоте в прямоугольном": $h$ проведенная из угла $90^o$ делит исходный треугольник на два ему подобных. Ведь высота поделила треугольник на два прямоугольных треугольника , причем с одинаковыми острыми углами , потому что , если одни из острых углов треугольников совпадают, а их сумма двух $90^o$ , то и другие совпадут $\Rightarrow$ все эти треугольники подобные между собой и исходному.
- 7. "Еще о высоте " : высота равна среднегеометрическому отрезков, на которые она делит гипотенузу:
про $CH=h=\sqrt{AH\cdot BH}$ , $h\cdot c=a\cdot b$ . - 8. "О медиане, проведенной к гипотенузе" : она равна половине гипотенузы $CM=\frac{AB}{2}$ , а так же радиусу описанной окружности $CM=R$. Точка $M$ на гипотенузе равноудалена от всех трех вершин.
Интерактивные Упражнения: Решить задачи №51 - №56
Интерактивные Упражнения: