- Угол состоит из вершины, двух сторон (два луча) и внутренней области.
- Угол - внутренняя область, образованная двумя пересекающимися прямыми, или отрезками.
- .... Они называются сторонами угла, а точка пересечения этих сторон называется вершиной угла.
- Равенство углов: два угла равные, если они полностью совпадают при наложении, как равные фигуры.
- Что значит равные фигуры?
- a. Если при наложении (как твердого тела) одной фигуры на другую фигуру, эти фигуры полностью (без зазоров) совместятся,
- b. Если с помощью движений на плоскости (параллельное перемещение, повороты, отражения) одну фигуру можно совместить с другой.
- Складывание углов - Если один угол приложить к другому так, чтобы вершины совпали и одна сторона была общей ....
- Сложение и вычитание углов : целый угол равен сумме составляющих углов: $\angle AOC = \angle AOB + \angle BOC$
- Аддитивность градусной меры углов - градусная мера полного угла равна сумме углов, составляющих весь угол.
- Если лучи дополняют друг друга до прямой, то оба образующихся угла называются развернутыми - $180^0$ градусов.
- Развернутый угол– это половина полного $360^0$ угла. Прямой $90^0$ угол – половина развернутого.



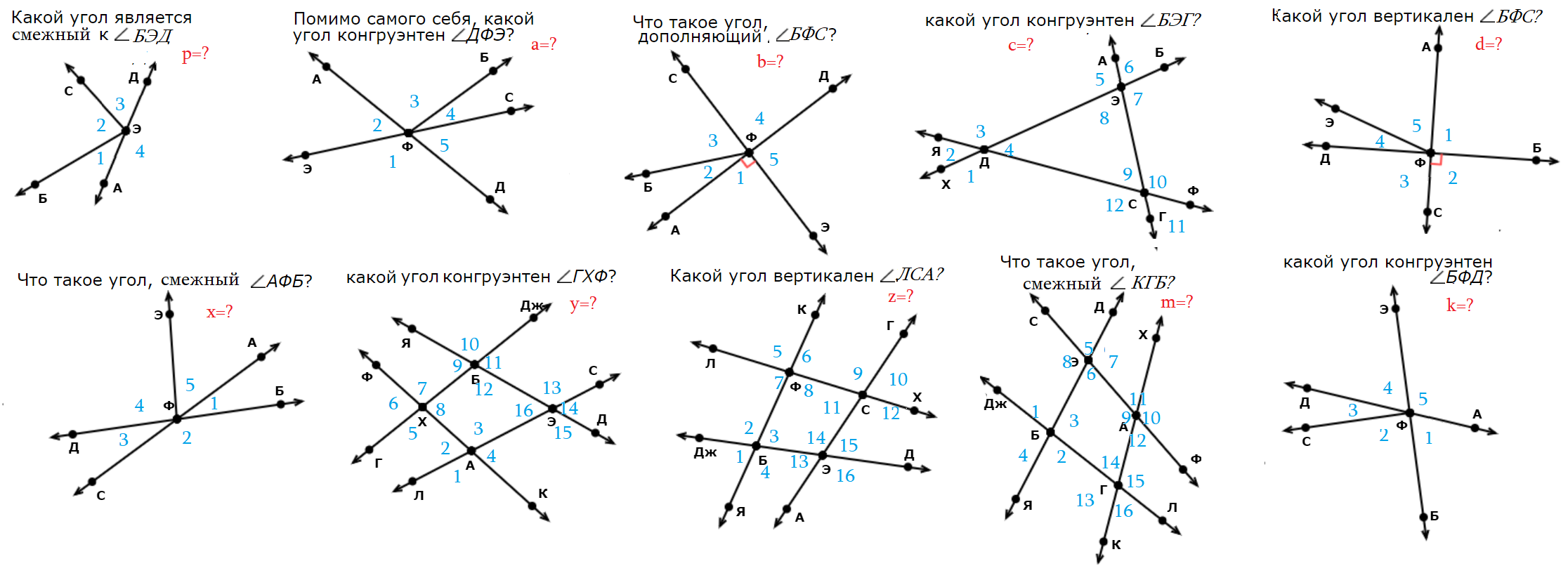
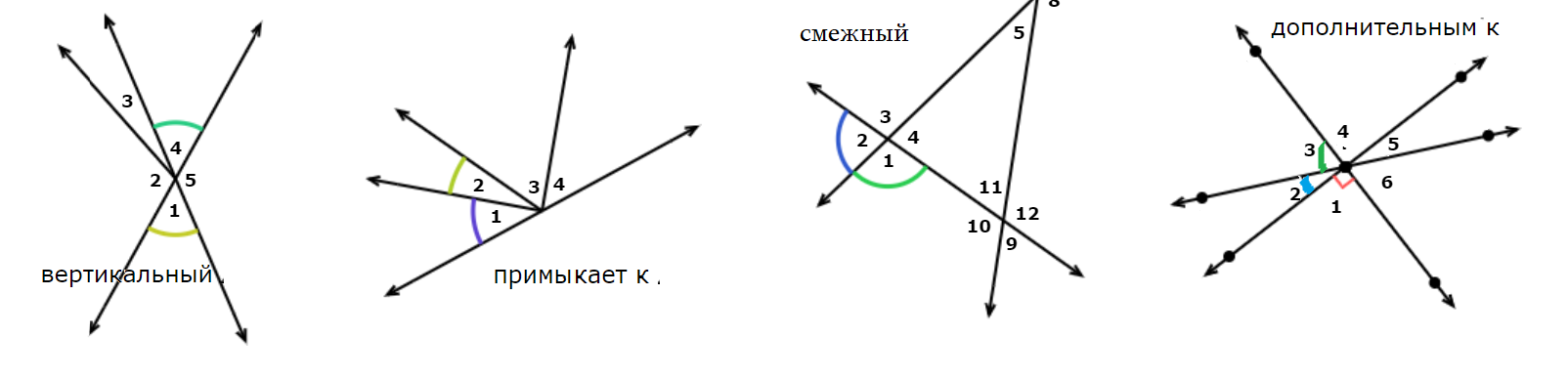
Смежные и вертикальные углы
- Пара углов с общей вершиной может быть смежными или вертикальными, если у них общая вершина, а стороны ... ??
- Конгруэнтными, или равными называются пара углов, которые при наложении области углов совпадают.
Дополнительными, (до 90 $^o$) называются пара углов, которые при прикладывании образуют прямой угол, $90^o$ .
Смежные углы имеют общую вершину, одну общую сторону, а другие стороны являются продолжениями друг друга.
- Примыкающие, прилегающие углы: соседние углы имеют общую вершину и сторону, но не имеют внутренних точек.
- Смежные углы имеют меры, которые добавляются, складываются до развернутого угла, 180°.
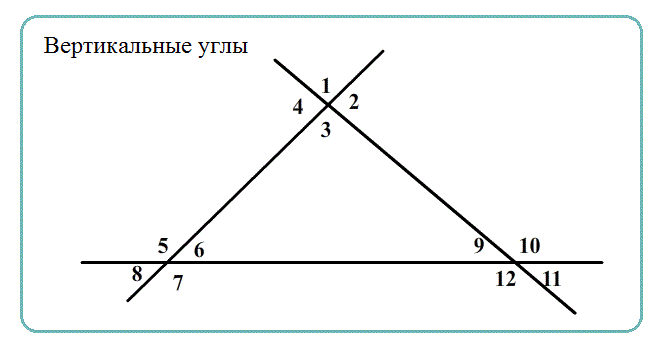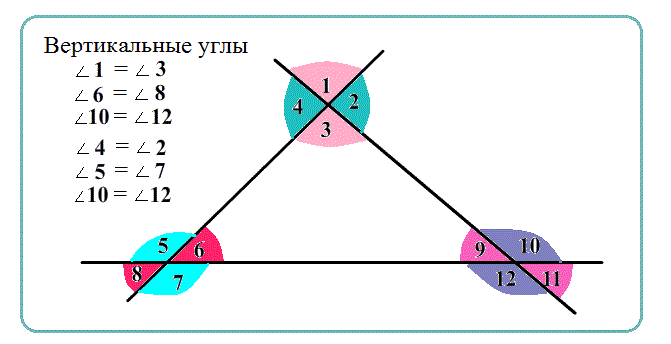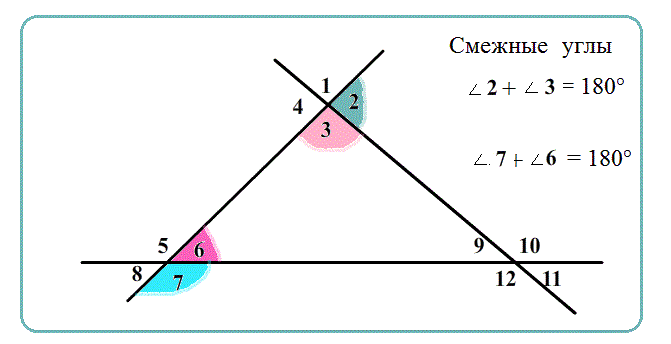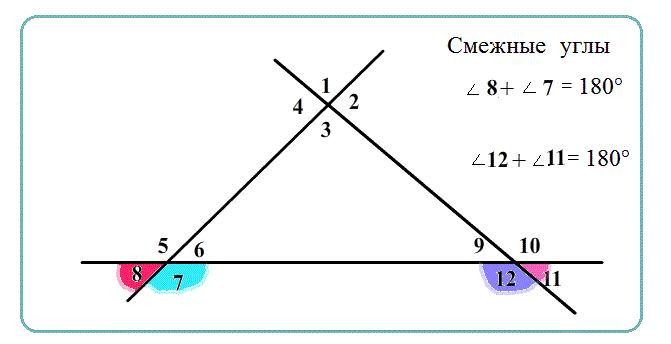
Вертикальные углы имеют общую вершину, а каждая сторона одного угла является продолжением стороны второго угла.
- Смежные углы прикладываются друг к другу одной общей стороной. А другие стороны - противоположные лучи.
- Если стороны одного угла направить ровно в противоположное направление от вершины, то получится вертикальный с ним угол.
- Вертикальные углы - это углы, образующиеся друг против друга при пересечении двух линий
Аддитивность, складываемость: Угол равен сумме составляющих его частей, углов.
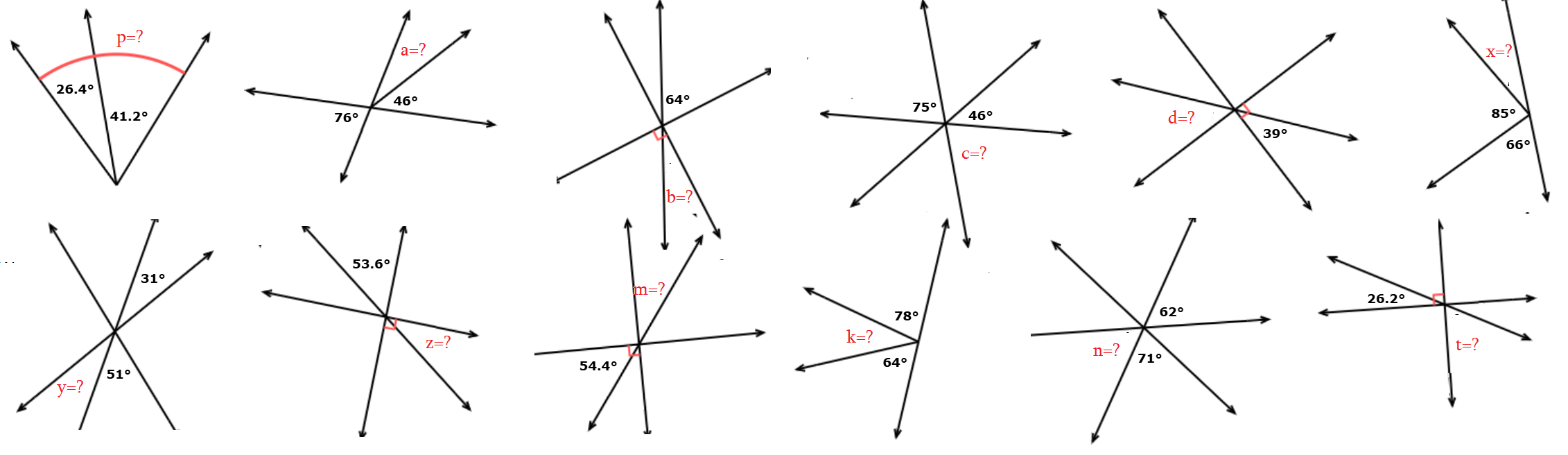
Теорема Сумма смежных углов равна развернутому углу – 180о.
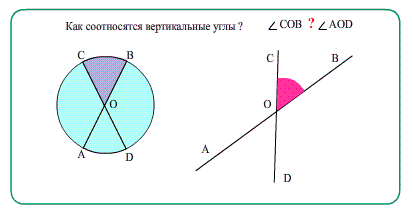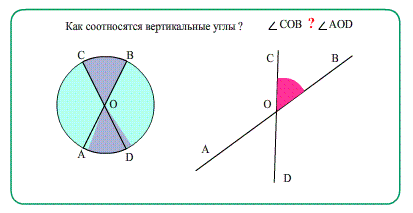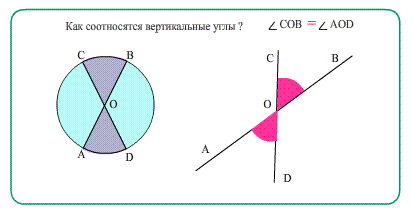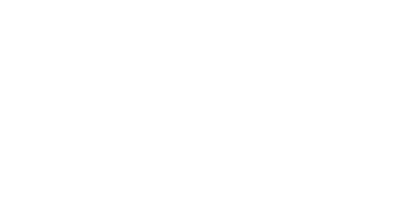
Теорема Вертикальные углы равны. При наложении друн-на-друга такие углы совпадяют.
Равенство для пары вертикальных: $\angle {(угол)}=\angle {(углу, вертикальному.с.ним)}$
Равенство для пары смежных: $\angle {(угол)}=180^o-\angle {(углу, смежнему.с.ним)}$
Равенство для пары дополняющих: $\angle {(угол)}=90^o-\angle {(углу,дополняющего.его)}$
вертикальные: ∠α = ∠β смежные: ∠α = 180° - ∠β дополняющие: ∠α = 90° - ∠β
На рисунке изображены две пары вертикальных углов: ∠АОD и ∠СОB, а также ∠AOC и ∠ВОD.
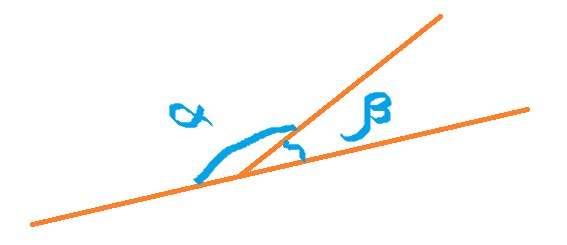
Задача 1: Найдите смежные углы, угол $α$ и угол $β$, если $α$ в $3,5$ раза больше $β$.
- Решение: сумма смежных $α$ и $β$ углов равна $180°$....значит, $α + β = 180°$.
- $α$ в $3,5$ раза больше $β$ ... значит, $α = 3,5β$.
- Комбинируем два равенства, подставим одно в другое: $α + β = 3,5β + β = 4,5β = 180°$
- Решим уравнение $4,5β = 180°$, найдем $\beta=\frac{180}{4,5}=40$
- тогда $β = 40°$ . а $3,5$ раза больший угол будет равен $α = 140°$
- Таким образом, если мы знаем соотношение между двумя смежными углами, то мы можем найти их меры.
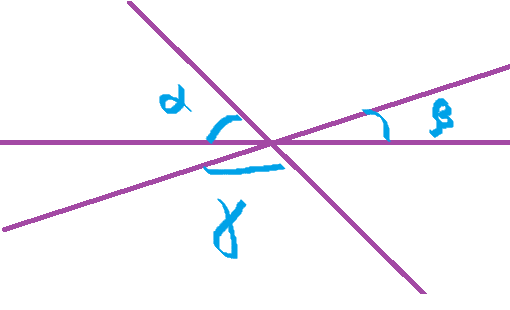
Задача 2: Три прямые пересекаются в точке $O$. Найдите угол $γ$, если $α = 55°$, а $β = 40°$.
- Решение: Угол, вертикальный с углом $γ$, равен с ним. "Три смежных" угла?
- По свойству вертикальных углов имеем, что сумма мер трёх углов равна $180°$, $\alpha+\beta+\gamma=180$
- Подставим значения известных углов $55+40+\gamma=180$. Найдем неизвестный угол.
- Искомый угол $γ$ имеет меру $85°$.
Задача 3: См. на рис. выше $OL$ , $OK$ - биссектриссы углов. Доказать, что всегда: 1) Угол между биссектрисами смежных углов равен $90^o$. 2) Угол между биссектрисами вертикальных углов равен $180^o$.
- Решение: Поскольку $OL$ – биссектриса угла $∠BOA$, то угол $∠LOB$ = $\frac{\alpha}{2}$ ,
- аналогично $∠BOK$ = $\frac{\beta}{2}$ .
- $∠LOK$ = $∠LOB$ + $∠BOK$ = $\frac{\alpha}{2}$ + $\frac{\beta}{2}$ = $\frac{\alpha+\beta}{2}$.
- Сумма углов $α + β$ равна $180^о$, поскольку данные углы – смежные.


Полезные вопросы, примеры. Решите наизусть:
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- В каком случае получается больше пар вертикальных: при пересечении трех прямых в одной точке или в трех точках?
- Найдите углы смежные ∠α и ∠β, если ∠β меньше ∠α в 3 раза.
- Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 52°
- Найдите смежные углы ∠b и ∠d, если ∠b = 1/4∠d.
Пары смежных (вертикальных) углов имеют одну, общую вершину.
Смежные, +=180, Т-образ: От точки отрезка исходит луч, 2 примыкающих угла. Общая вершина.

Вертикальные, = =, Х-образ: При пересечении двух отрезков возникающие противоположные 2 угла. Общая вершина.

Решаем устно:

Упражнения (A):
Упражнения (B):
Упражнения (С):