Основные свойства площадей фигур:
- Равные фигуры имеют равные площади. Две фигуры состоящие из одинаковых кусков - равновеликие.
- Аддитивность: Площадь фигуры, разрезанной на несколько частей, равна сумме площадей этих частей ;
- Площадь прямоугольника равна произведению ширины на длину ... произведение сторон.
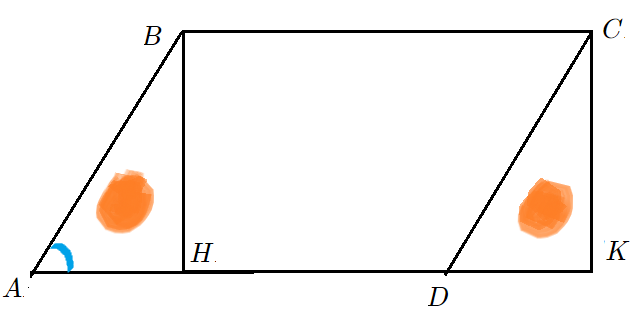
Задача 1: В параллелограмме известны стороны $7$, $10$ и синус угла между ними $\frac{1}{2}$. Найти площадь параллелограмма.
- Решение: Опустим высоты $BH$ и $CK$ на основание $AD$ . Они помогут "увидеть" площадь.
- Что есть синус $\angle BAH$ в прямоугольном треугольнике $\bigtriangleup ABH$? Отношение катета $BH$ к гипотенузе $AB$.
- Формула синуса позволит выразить высоту $BH$ через сторону $AB$ и синус $\frac{1}{2}$. Высота $CK$ такая же.
- Параллелограмм $ABCD$ состоит из кусков: $\bigtriangleup ABH$ и $4$-угольник $HBCD$. Площадь - сумма площадей кусков.
- Прямоугольник $HBCK$ состоит из кусков $HBCD$ и $\bigtriangleup DCK$. Площадь также "сумма кусков".
- Треугольники $\bigtriangleup ABH$ и $\bigtriangleup DCK$ одинаковые. Значит, параллелограмм и прямоугольник равновеликие.
- Площадь Параллелограмма $ABCD$ так же, как прямоугольника $HBCD$ равна высота на основание.
- $S_{ABCD}=S_{ABH}+S_{HBCD}=S_{HBCD}+S_{DCK}=S_{HBCK}=BH\cdot HK=AB\cdot\sin \angle BAD\cdot AD=7\cdot\frac{1}{2}\cdot10$
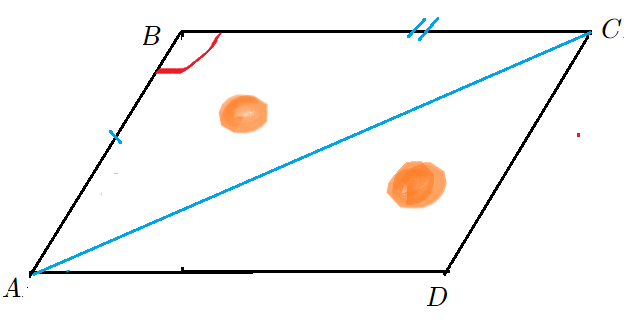
Теорема "о площади параллелограмма и треугольника через синус угла":
- Площадь параллелограмма равна произведению сторон на синус угла параллелограмма:
- Формулы $S=a\cdot b\cdot\sin \angle BAD$ $S_{ABCD}=AB\cdot BC\cdot\sin D$
- Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними.
- Формулы $S=\frac{1}{2}\cdot a\cdot b\cdot\sin \angle C$ $S_{\bigtriangleup ABC}=\frac{1}{2}\cdot AB\cdot BC\cdot\sin \angle CBA$
Площадь треугольника также легко получить через площадь параллелограмма, равновеликого с двумя треугольниками, приставленными друг к другу по диагонали. Тогда площадь одного треугольника будет равна половине площади параллелограмма с тем же основанием и с той же высотой.
Задача 2: Диагонали четырехугольника делятся точкой пересечения на отрезки $3$, $5$ и $6$, $7$ . Синус угла между диагоналями $0,2$. Найти площади треугольников и всего четырехугольника.
- Дано: $BO=3$ $OD=5$ $CO=6$ $AO=7$ ... угол между $\sin\angle AOB=0,2$. Найти: $S_{ABCD}=?$.
- Решение: Диагонали делят четырехугольник на 4 треугольника. Площадь = сумме 4-х площадей.
- Аддитивность: $S_{ABCD}=S_{\bigtriangleup AOB}+S_{\bigtriangleup BOC}+S_{\bigtriangleup COD}+S_{\bigtriangleup AOD}$.
- Площадь одного из них по формуле: $S_{\bigtriangleup AOB}=\frac{1}{2}\cdot AO\cdot OB\cdot \sin \angle AOB=\frac{1}{2}\cdot 7 \cdot 3\cdot 0,2=2,1$
- Каковы синусы остальных углов? Свойство: Синусы смежных углов равны: $\sin\angle BOC=\sin\angle COD=\sin\angle AOD=0,2$
- Тогда, площади других треугольников $\frac{1}{2}\cdot 3 \cdot 6\cdot 0,2=1,8$ $\frac{1}{2}\cdot 6 \cdot 5\cdot 0,2=3$ $\frac{1}{2}\cdot 5 \cdot 7\cdot 0,2=3,5$
- Площадь четырехугольника равна сумме этих площадей Ответ: $S_{ABCD}=2,1+1,8+3+3,5=10,4$
Теоретически, по-другому: Распишем получение площади $S_{ABCD}$ в буквах, без числовых значений:
- $\frac{1}{2}\cdot OA\cdot OB\cdot \sin \angle AOB+\frac{1}{2}\cdot OB\cdot OC\cdot \sin \angle AOB+\frac{1}{2}\cdot OC\cdot OD\cdot \sin \angle AOB+\frac{1}{2}\cdot OD\cdot OA\cdot \sin \angle AOB$
- Вынос за скобки множителей $S_{ABCD}=\frac{1}{2}\cdot \sin \angle AOB\cdot \left(OA\cdot OB+OB\cdot OC+OC\cdot OD+OD\cdot OA\right)$
- $S_{ABCD}=\frac{1}{2}\cdot \sin \angle AOB\cdot \left(OB\cdot\left(OA+OC\right)+OD\cdot\left(OA+OC\right)\right)=\frac{1}{2}\cdot \sin \angle AOB\cdot AC \cdot (OB+OD)$
- Получаем $S_{ABCD}=\frac{1}{2}\cdot AC \cdot BD\cdot \sin \angle AOB$ $\Rightarrow$ $S_{ABCD}=\frac{1}{2}\cdot (7+6) \cdot (3+5)\cdot 0,2=13\cdot 0,8=10,4$

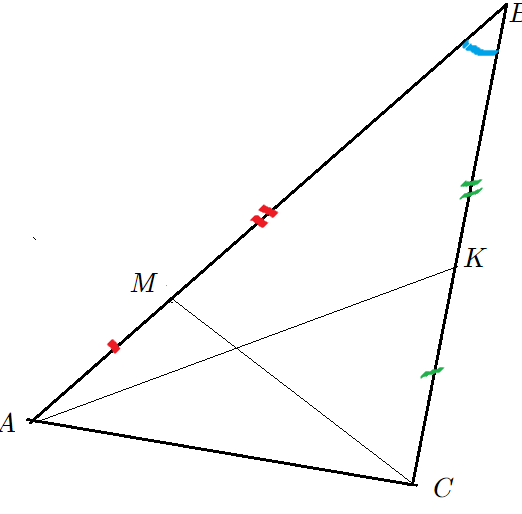
Задача 3: В треугольнике известны стороны $AB=10$ , $BC=12$ и угол $\angle ABC=30$ . Точка $M$ делит сторону $AB$ в отношении 3 : 5, а точка $K$ делит сторону $BC$ в отношении 2 : 3. Найти площади и отношение площадей треугольников $ABK$ и $MBC$.
- Дано: $AB=10$, $BC=12$, $\frac{AM}{MB}=\frac{3}{5}$, $\frac{BK}{KC}=\frac{2}{3}$, $\angle ABC=30$. Найти: $\frac{S_{\bigtriangleup ABK}}{S_{\bigtriangleup MBC}}=?$
- Точка делит отрезок в известном соотношении. Находим части как систему уравнений $\frac{x}{y}=?$ $x+y=?$
- $\frac{AM}{MB}=\frac{3}{5}$, аддитивность $AM+MB=AB=10$ $\Rightarrow$ $\frac{AM}{AB}=\frac{3}{3+5}$ $\Rightarrow$ $AM=\frac{15}{4}$, $MB=\frac{25}{4}$
- $\frac{BK}{KC}=\frac{2}{3}$, $BK+KC=12$ из свойств пропорций $BK=\frac{24}{5}$, $KC=\frac{36}{5}$
- Найдем площадь через синус $S_{\bigtriangleup ABK}=\frac{1}{2}\cdot AB \cdot BK \cdot \sin \angle ABC = \frac{1}{2}\cdot 10 \cdot \frac{24}{5} \cdot \sin 30= 24 \cdot 0,5=12$
- В треугольнике $MBC$ тот же угол, $S_{\bigtriangleup MBC}=\frac{1}{2}\cdot MB \cdot BC \cdot \sin \angle ABC = \frac{1}{2}\cdot \frac{25}{4} \cdot 12 \cdot 0,5=\frac{75}{4}$
- отношение площадей треугольников $\frac{S_{\bigtriangleup ABK}}{S_{\bigtriangleup MBC}}=\frac{12}{\frac{75}{4}}=\frac{16}{25}$ Ответ: $\frac{16}{25}$
Замечание, продолжение: Можно ли найти отношение площадей при неизвестных значениях сторон и угла?
- Зная лишь как делят точки $M$ и $K$ стороны треугольника, на какие пропорции ?!
- Дано только $\frac{AM}{MB}=\frac{3}{5}$, $\frac{BK}{KC}=\frac{2}{3}$. Выразим отрезки через стороны $AB$ и $BC$.
- Выразим площади $S_{\bigtriangleup ABK}$ , $S_{\bigtriangleup MBC}$ также через стороны $AB$ и $BC$ и угол $\angle ABC$.
- Составим отношение площадей, выразим через стороны и угол. Что получится? Что можно сделать, ?
Теорема "о площади четырехугольника через диагонали и синус угла":
- Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними:
- Формулы $S=\frac{1}{2}\cdot d_1 \cdot d_2 \cdot\sin \angle \alpha$ $S_{ABCD}=\frac{1}{2}\cdot AC \cdot BD\cdot \sin \angle AOB$
- Площадь ромба равна половине произведения диагоналей. ... диагонали перпендикулярны!
- Формулы $S=\frac{1}{2}\cdot d_1 \cdot d_2=\frac{1}{2}\cdot AC \cdot BD$ $\angle AOB=90$ $\sin \angle AOB=1$
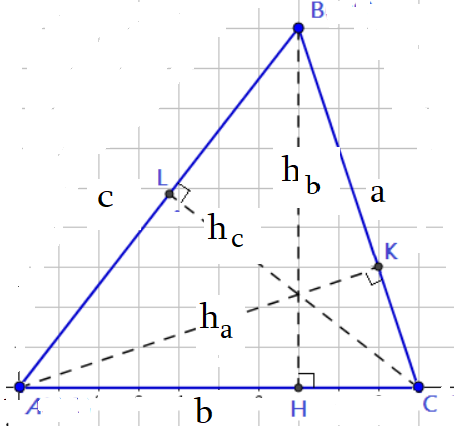
Формулы площади треугольника:
$S=\frac{a\cdot h_a}{2}=\frac{a\cdot b\cdot\sin C}{2}$ $S=\frac{b\cdot h_b}{2}=\frac{b\cdot c\cdot\sin A}{2}$ $S=\frac{c\cdot h_c}{2}=\frac{c\cdot a\cdot\sin B}{2}$.
$\sin A=\frac{h_b}{c}=\frac{h_c}{b}$ $\sin B=\frac{h_a}{c}=\frac{h_c}{a}$ $\sin C=\frac{h_b}{a}=\frac{h_a}{b}$.
$S_{ABC}=\frac{1}{2}\cdot AC\cdot BC\cdot\sin C$ $S_{ABC}=\frac{1}{2}\cdot AB\cdot BC\cdot\sin B$ $S_{ABC}=\frac{1}{2}\cdot AC\cdot AB\cdot\sin A$ .
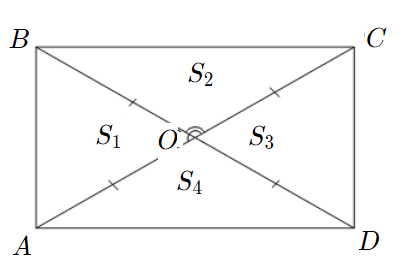
Задача 4: В прямоугольнике диагонали $10$ и угол между ними $30$. Найти площадь.
- Дано: $ABCD$ - прямоугольник , $AC=10$ , $\angle AOB=30$ Найти: $S_{ABCD}$ .
- Решение: В прямоугольнике диагонали равны и пересекаются по середине $AO=OB=5$
- $\bigtriangleup AOB$ и $\bigtriangleup COD$ равные $\Rightarrow$ $S_1=S_3$ ;
- $\bigtriangleup BOC$ и $\bigtriangleup AOD$ равные $\Rightarrow$ $S_2=S_4$ .
- Смежные, $\angle BOC=180-\angle AOB=150$. Найдем отношение $\frac{S_1}{S_2}=\frac{\frac{1}{2}AO\cdot OB\cdot\sin30}{\frac{1}{2}BO\cdot OC\cdot\sin150}$
- $\sin30=\sin\left(180-30\right)=\sin150$. тогда $\frac{S_1}{S_2}=\frac{\frac{1}{2}\cdot5\cdot5\cdot\sin150}{\frac{1}{2}\cdot5\cdot5\cdot\sin150}=1$ Значит, $S_1=S_2$
- Аналогично: $\frac{S_3}{S_4}=\frac{\frac{1}{2}DO\cdot OC\cdot\sin30}{\frac{1}{2}AO\cdot OD\cdot\sin150} =1$ $\Rightarrow$ $S_3=S_4$, площади равные.
- Диагонали рассекают прямоугольник на четыре равновеликих: треугольника $S_1=S_2=S_3=S_4$ .
- ... тогда, по свойству аддитивности площадей $S_1=S_2=S_3=S_4=\frac{1}{4}S_{ABCD}$ .
- $S_{AOB}=S_1=\frac{1}{2}AO\cdot OB\cdot \sin 30=\frac{1}{2}\cdot 5\cdot 5\cdot \frac{1}{2}=\frac{25}{4}$ $\Rightarrow$ $S_{ABCD}=4\cdot\frac{25}{4}$
- Найдя площадь АОВ, нашли площадь прямоугольника умножением на 4. Ответ: $S_{ABCD}=25$
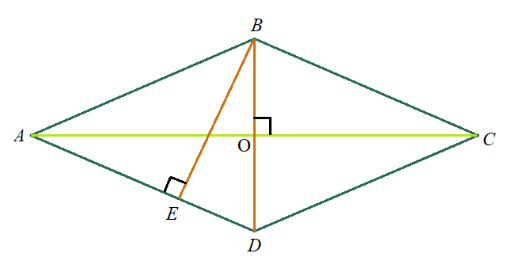
Задача 5: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Дано: ромб $ABCD$ , $BD=13$, высота $EB=12$ , Найти: $S_{ABCD}$ .
- Решение: прямоугольный $\bigtriangleup BED$, подобен тем, на которые ромб делится диагоналями:
- $\bigtriangleup BED \sim \bigtriangleup AOD=\bigtriangleup AOB=\bigtriangleup COB=\bigtriangleup COD$ . Одинаковый "состав" углов. Все прямоугольные,
- Прямоугольный $\bigtriangleup BED$, по Пифагору выразим катет $DE=\sqrt{BD^2-BE^2}=5$
- Диагонали в ромбе делятся пополам: $BO=OD=\frac{BD}{2}=6,5$ $AO=\frac{AC}{2}$ $AC=2\cdot AO$
- Для нахождения площади ромба нам нужно найти вторую диагональ.
- $\bigtriangleup BED \sim \bigtriangleup AOD$ $\Rightarrow$ $\frac{AO}{BE}=\frac{OD}{ED}$ $\Rightarrow$ $AO=\frac{OD\cdot BE}{ED}=\frac{6,5\cdot 12}{5}=15,6$ $AC=2\cdot AO=31,2$
- Ответ: Площадь ромба через диагонали: $S_{ABCD}=\frac{1}{2}\cdot AC\cdot BD=0,5\cdot 31,2\cdot13=202,8$


Задача 6. Площадь равнобедренного треугольника равна $100$ , а угол при вершине $30^o$ 1) Найти его боковые стороны . 2) Найти тригонометрию $15^o$
- Решение: 1) Известны площадь и угол, значит используем формулу площади через синус $30^o$ .
- Пусть боковая сторона $a$ , $S=\frac{1}{2}a\cdot a\cdot\sin30$ , тогда $100=\frac{1}{2}a^2\cdot\sin30$ $\Leftrightarrow$ $100=\frac{1}{2}a^2\cdot\frac{1}{2}$ $\Rightarrow$
- $a=\sqrt{400}=20$ Ответ: $a=20$
- 2) По теореме косинусов найдем основание $c=\sqrt{a^2+a^2-2\cdot a\cdot a\cdot\frac{\sqrt{3}}{2}}=a\sqrt{2-\sqrt{3}}$
- Из вершины равнобедренного угла проведем биссектрису к основанию. По свойству равнобедренности
- она будет и высотой $h$ (треугольник поделится на 2 прямоугольных с углами 15 градусов) и медианой,
- а значит основание поделится пополам , как и угол 30 у вершины поделится по 15 градусов.
- По прямоугольнему треугольнику (половинка): $\sin15=\frac{0,5\cdot c}{a}=\frac{0,5\cdot a\cdot\sqrt{2-\sqrt{3}}}{a}=\frac{\sqrt{2-\sqrt{3}}}{2}$
- Площадь через основание $S=\frac{1}{2}\cdot c\cdot h$, найдем высоту $h=\frac{2\cdot S}{c}=\frac{2\cdot0,5\cdot a^2\cdot\sin30}{a\cdot\sqrt{2-\sqrt{3}}}=\frac{a}{2\cdot\sqrt{2-\sqrt{3}}}$
- В прямоугольном треугольнике стороны $h$, $\frac{c}{2}$, $a$. Тогда $\cos15=\frac{h}{a}=\frac{\frac{a}{2\cdot\sqrt{2-\sqrt{3}}}}{a}=\frac{1}{2\cdot\sqrt{2-\sqrt{3}}}$
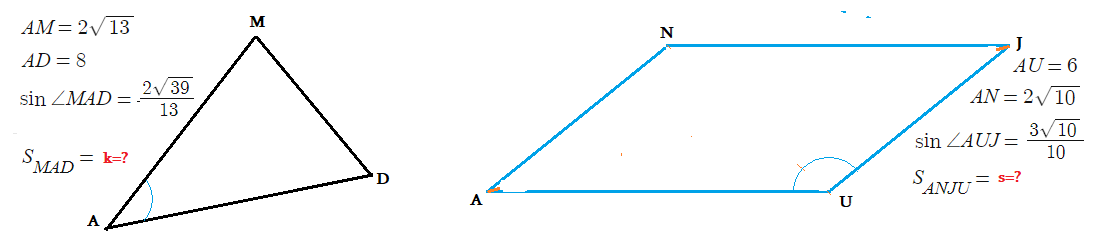
Упражнения (А):
Упражнения (В):