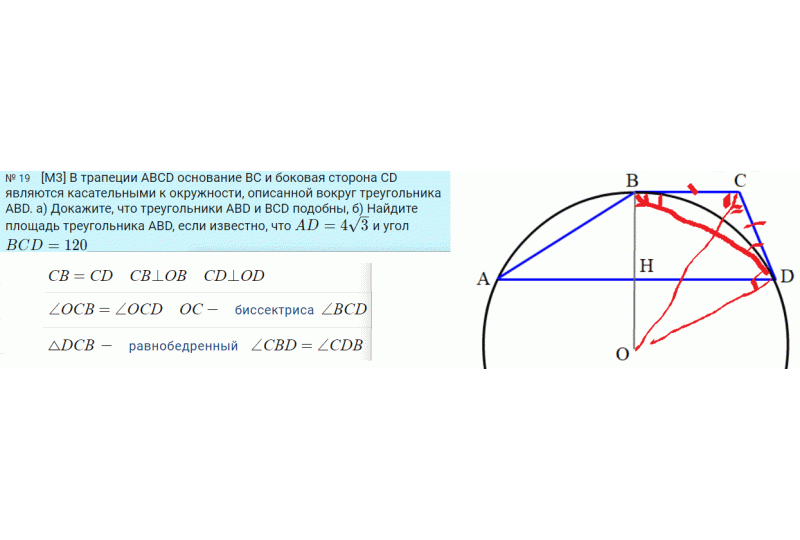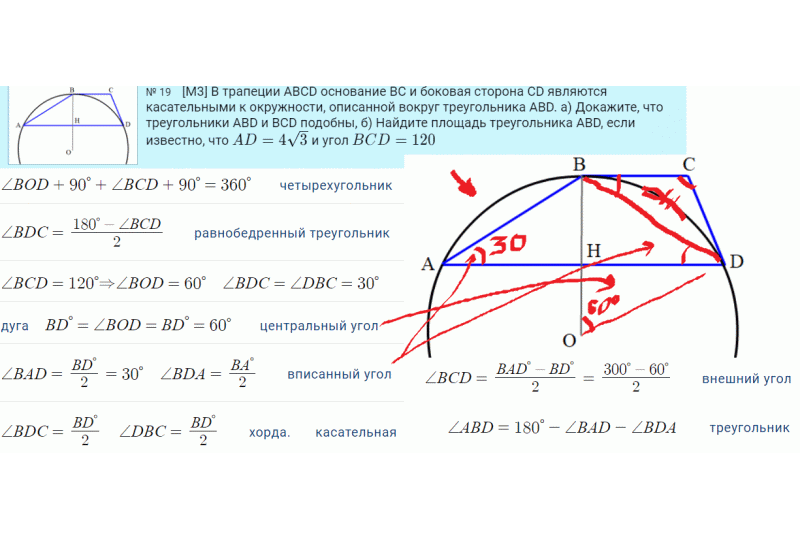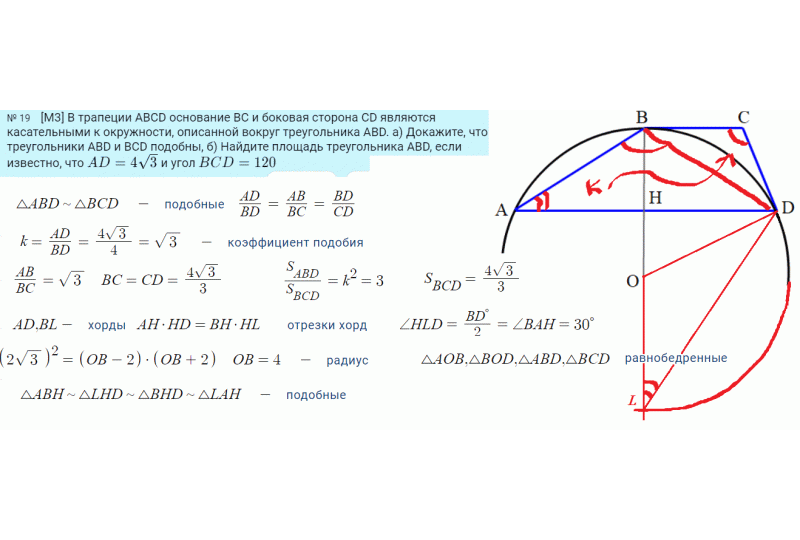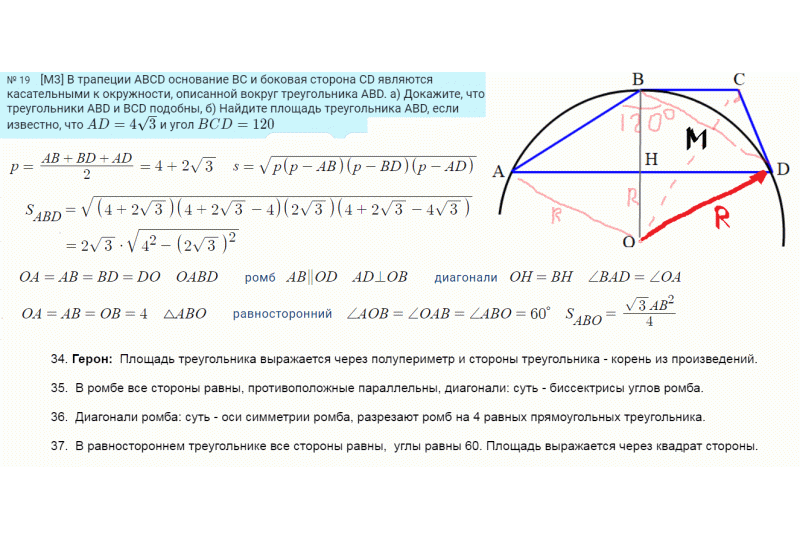
Задача: В трапеции ABCD основание ВС и боковая сторона CD являются касательными к окружности,
описанной вокруг треугольника ABD. а) Докажите, что треугольники ABD и BCD подобны,
б) Найдите площадь треугольника ABD, если известно, что AD = 4 и угол BCD = 120.
Не просто решим, а в правильном порядке решим и проанализируем всесторонне (образование, самообучение)!
1. Во-первых: Надо "взгляд на задачу, рисунок" и искать в нём все свойства, формулы. Что видим?
2. Каждое обнаруженное свойство "дожать" - сделать выводы, написать формулы, равенства.
3. Формулировать утверждения: конкретно по задаче, общие утверждения.
4. Собственно решение: цепочка свойств, равенств, вычислений, приводящих к результату.
Взгляд I: Касательные, равнобедренный, прямой угол, Пифагор

1. Из одной точки $C$ проведённые к окружности две касательные $CB$ и $CD$ равны.
2, Касательные перпендикулярны радиусу, проведённому из центра к точке касания.
3. Углы при основании равнобедренного треугольника равны между собой.
4. Пифагора: сумма квадратов катетов треугольника равна квадрату гипотенузы.
Взгляд II: Углы в треугольнике, углы при параллельных, накрест лежащие,
Параллельные линии и окружность: хорды, дуги. Подобие.
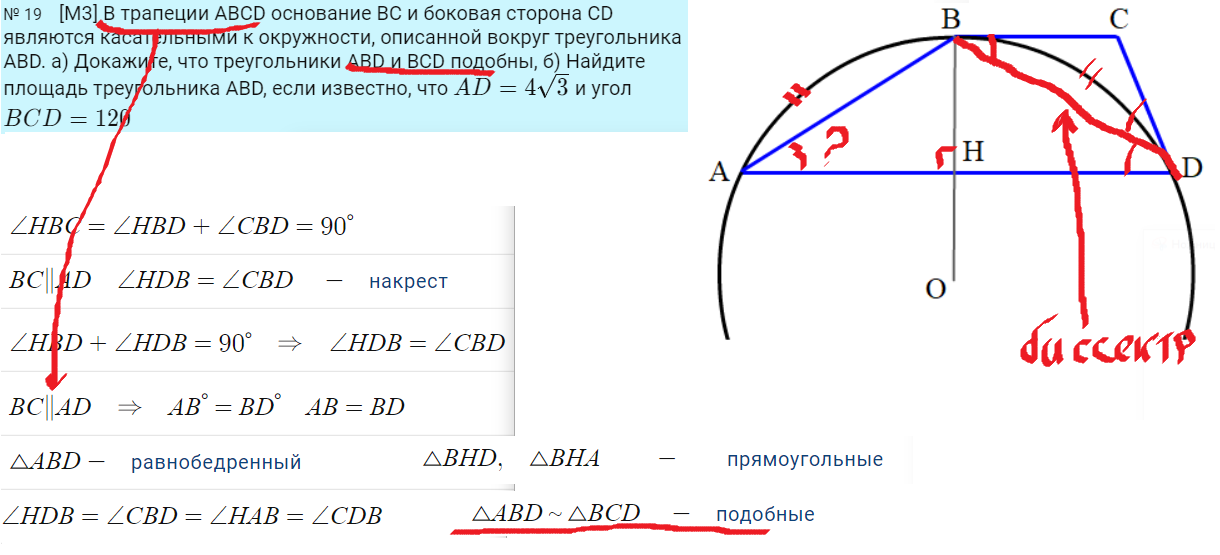
5. Сумма острых углов прямоугольного треугольника равна 90 градусов.
6. В трапеции основания параллельны, накрест лежащие у диагоналей углы равные.
7. Накрест лежащие углы при параллельных и секущей равны.
8. Аддитивность угла: целый угол равен сумме углов, составляющих части целого.
9. Параллельные линии отсекают от окружности равные дуги и равные хорды (трапеция также).
10. Если у треугольников "состав углов" одинаковый, то такие треугольники подобны.
Взгляд III: Сумма углов многоугольника. Углы при окружности, связь с дугами:
центральный, вписанный, внешний, внутренний, м/д хорда/касательной.
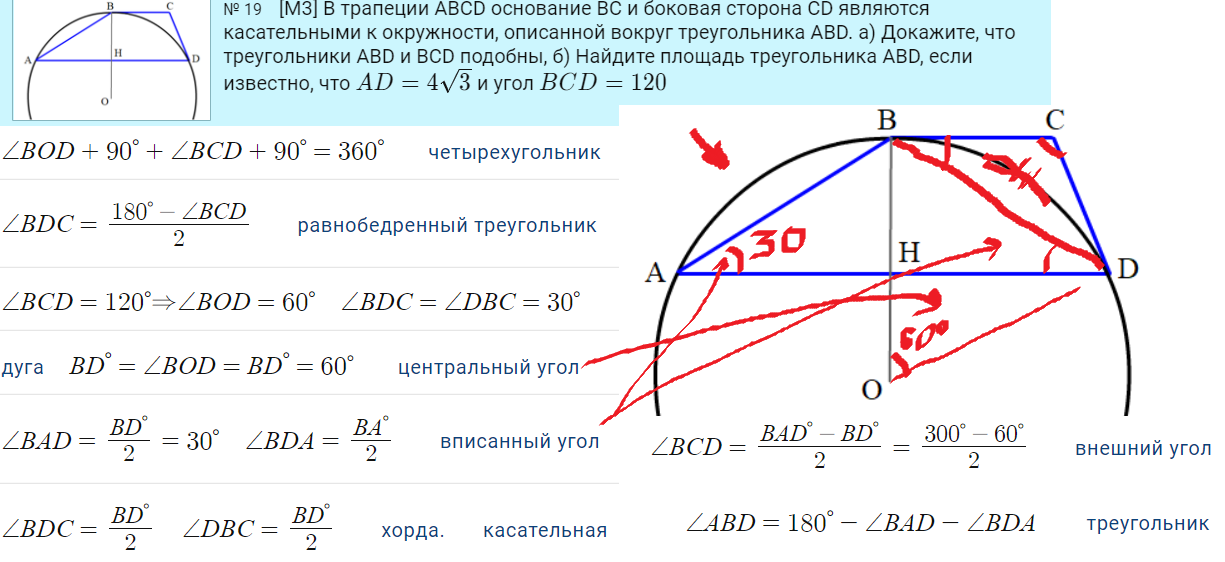
11. Сумма углов четырёхугольника = 360, сумма углов треугольника = 180 градусов.
12. Центральный угол равен градусной мере дуги опирания.
13. Вписанный угол равен половине градусной меры дуги опирания.
14. Внешний угол окружности (между секущими) = полуразности отсечённых дуг.
15. Угол между хордой и касательной равен половине "зажатой" между ними дуги.
16. Внутренний угол окружности (между хордами) = полусумме отсекаемых дуг.
Взгляд IV: Свойства равнобедренных, прямоугольных. Формулы Площадей.

17. В равнобедренном треугольнике от вершины опущенные высота, медиана и биссектриса совпадают.
18. В равнобедренном треугольнике (и в трапеции) есть симметрия: слева и справа все одинаково!
19. В прямоугольном треугольнике катеты, гипотенуза выражают друг друга через тригонометрии углов.
20. В прямоугольном треугольнике катет напротив 30 градусов равен половине гипотенузы.
21. Площадь треугольника равна половине произведения стороны и высоты, опущенной на эту сторону.
22. Площадь треугольника равна половине произведения двух сторон и синуса угла между ними.
Взгляд V: Подобие, коэффициент, отношение площадей (D2). Пересечение хорд.

23. В подобных треугольниках: коэффициент подобия равен отношению схожих отрезков.
24. В подобных фигурах: отношения схожих углов равны 1, т.е. составы углов равны. (D0).
25. В подобных: отношения схожих отрезков (сторон, высот, радиусов) равны коэффициенту. (D1).
26. В подобных фигурах отношения площадей равны коэффициенту в квадрате. (D2).
27. В подобных пространственных фигурах отношения объёмов равны коэффициенту в кубе.(D3).
28. При пересечении хорд произведения отрезков-частей для каждой хорды одинаковы.
Взгляд VI: Теоремы Синусов, Косинусов. Радиус и центр описанной окружности.

29. Т. Синусов: отношения для всех сторон к синусу противолежащего угла равны между собой..
30. ... и эти отношения равны удвоенному радиусу описанной окружкости вокруг треугольника.
31. Т. Косинусов: квадрат стороны равен сумме квадратов прочих - 2 * произведение их на косинус.
32. 4-х кратная площадь на радиус описанной равна произведению всех сторон треугольника.
33. Центр описанной окружности находится на пересечении срединных перпендикуляров к сторонам.
Взгляд VII: Еще: Формула Герона. Свойства ромба, диагонали. Равносторонний треугольник.

34. Герон: Площадь треугольника выражается через полупериметр и стороны треугольника - корень из произведений.
35. В ромбе все стороны равны, противоположные параллельны, диагонали: суть - биссектрисы углов ромба.
36. Диагонали ромба: суть - оси симметрии ромба, разрезают ромб на 4 равных прямоугольных треугольника.
37. В равностороннем треугольнике все стороны равны, углы равны 60. Площадь выражается через квадрат стороны.
Одна задача и сколько в ней геометрических свойств, утверждений, формул: В трапеции ABCD основание ВС и боковая сторона CD являются касательными к окружности, описанной вокруг треугольника ABD. а) Докажите, что треугольники ABD и BCD подобны, б) Найдите площадь треугольника ABD, если известно, что и угол
Клип: Все свойства и равенства задачи
Интерактивные упражнения: (задчи ЕГЭ №16):
