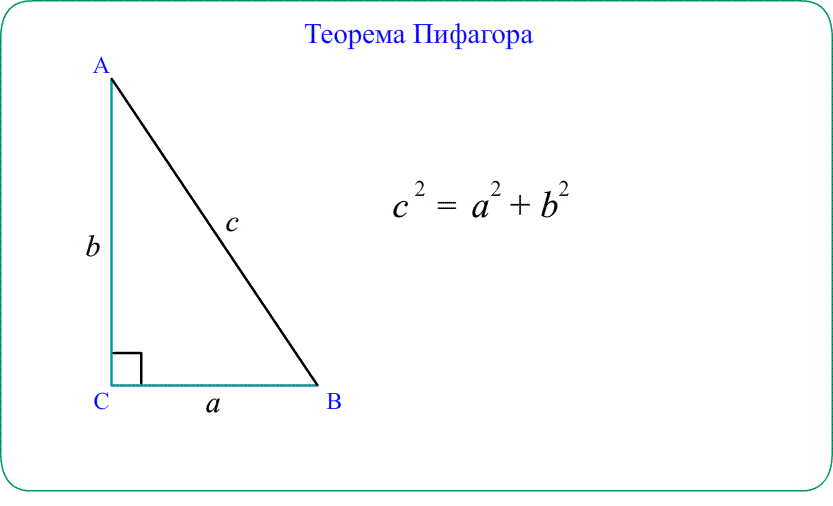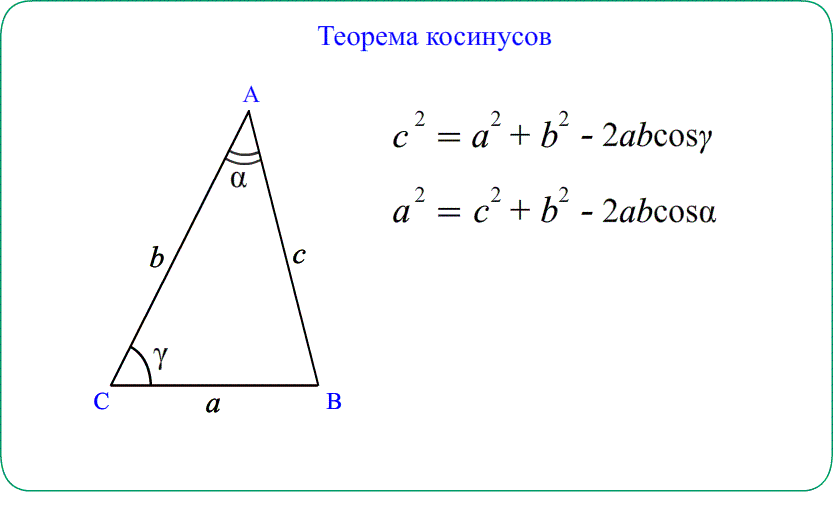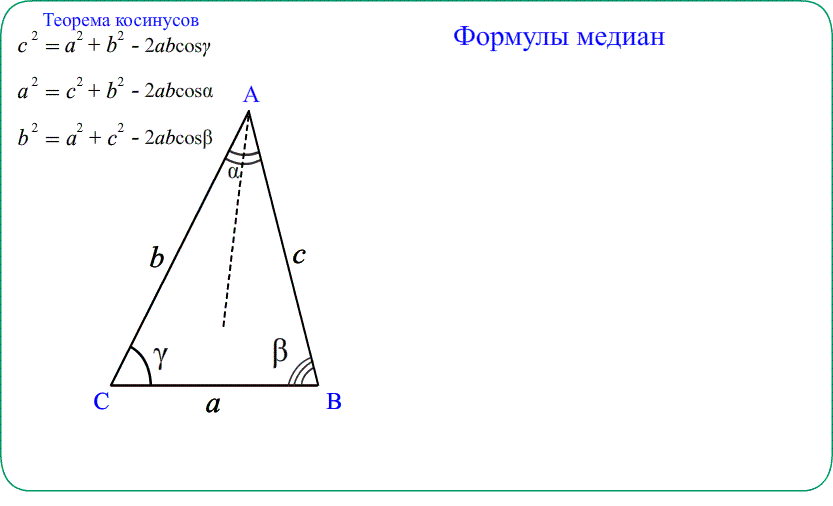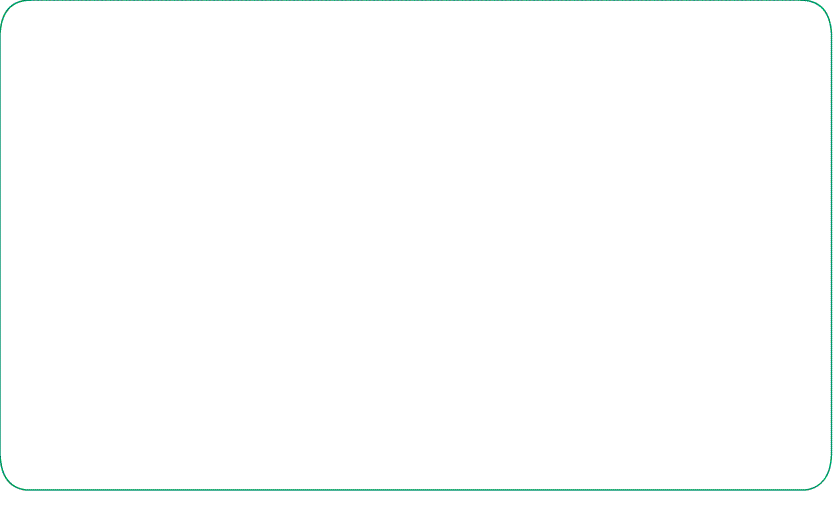
Теорема косинусов
Если в треугольнике даны две стороны и угол между ними, то такой треугольник один, единственный. Т.е. любой другой треугольник с такими данными будет в точности равен ему, по 2-му признаку равенства треугольников. Ну, раз единственный и неповторимый, то его третья сторона должна быть однозначно определяема.
Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух
других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
$AB^2=AC^2+BC^2-2\cdot AC\cdot BC\cdot\cos ACB$
Факты:
- Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит, и сам угол.
- Если из трех сторон и одного угла известны три величины, то четвертое неизвестное можно всегда вычислить.
- Теорема косинусов дает возможность вычислять медианы треугольника, применяя теорему к малым треугольникам.
- Для прямоугольного треугольника теорема косинусов "упрощается" до теоремы Пифагора $AB^2=AC^2+BC^2$.
А если угол тупой? Что означает тригонометрия больших углов?
$\cos130=-\cos50$, $\sin115=\sin65$ , $\tg135=-\tg45$.
Связь тригонометрии тупых углов $90 < \alpha < 180$ с тригонометрией острых выражается формулами:
$\sin\alpha=\sin\left(180-\alpha\right)$ $\cos\alpha=-\cos\left(180-\alpha\right)$ $\tg\alpha=-\tg\left(180-\alpha\right)$ $\ctg\alpha=-\ctg\left(180-\alpha\right)$
Если $b^2+c^2-a^2>0$, то $\alpha$ - острый; если $b^2+c^2-a^2=0$, то $\alpha$ - прямой; если $b^2+c^2-a^2<0$ , то угол $\alpha$ - тупой.
Расчет треугольников по теореме косинусов
Задача 1: В треугольнике $ABC$ сторона $AC$ равна $7\sqrt{3}$ см, сторона $BC$ равна $1$ см , угол $C$ = $150^o$ . Найти длину стороны $AB$.
- Решение: Применим теорему косинусов $AB^2=\left(7\sqrt{3}\right)^2+1-14\sqrt{3}\cos150$ .
- Тупой угол в $150^o$ выразим через острый : $\cos150=\cos\left(180-30\right)=-\cos30=-\frac{\sqrt{3}}{2}$. $\Rightarrow$
- $AB^2=147+1-28\sqrt{3}\left(-\frac{\sqrt{3}}{2}\right)$ , $AB^2= 148 + 21 = 169$ $\Rightarrow$ Ответ: $AB = 13$
Задача 2: В треугольнике $ABC$ сторона $AC$ равна $17$ см, сторона $BC$ равна $14$ см , угол $ACB$ = $60^o$ .
Найти длину третьей стороны .
- Решение: Из теоремы косинусов для угла $\angle ACB$ : $\Rightarrow$ $AB^2=17^2+14^2-2\cdot17\cdot14\cdot\cos60$ $\Rightarrow$
- квадрат стороны $AB^2= 289+196-238 = 247$ $\Rightarrow$ Ответ: $AB = \sqrt{247}$
Задача 3: В $\bigtriangleup ABC$ известны $AC=3$ , $BC=5$ см, $AB=6$ .
Найти косинус угла $C$ и медиану $BM$ .
- Решение: Из теоремы косинусов для стороны $AB$ выразим косинус требуемого угла $ACB$:
- $\cos ACB=\frac{AC^2+BC^2-AB^2}{2\cdot AC\cdot BC}=\frac{9+25-36}{30}=-\frac{1}{15}$ . Отрицательное значение косинуса говорит о том, что это тупой угол $>90^o$
- Для нахождения медианы $ВМ$ распишем еще раз теорему косинусов, но уже для треугольника $ВМС$ от угла $С$:
- $BM^2=BC^2+MC^2-2\cdot BC\cdot MC\cdot\cos C$ учтем, что медиана делит сторону пополам $MC=\frac{AC}{2}=1,5$
- Подставим $BM^2=25+2,25-2\cdot5\cdot1.5\cdot\left(-\frac{1}{15}\right)=27,25+1=28,25$, получим $BM=\sqrt{28,25}=0,5\sqrt{113}$
- Ответ: $\cos ACB=-\frac{1}{15}$ , $BM=0,5\sqrt{113}$ .
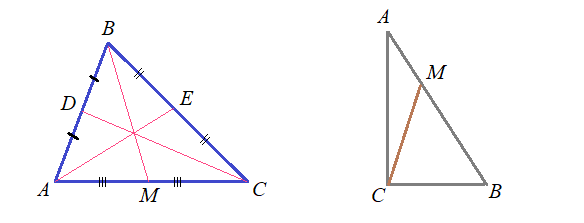
Задача 4: В прямоугольном $\bigtriangleup ABC$ известны $AB=9$ , $BC=3$ см ; $M$ делит $AB$ : $\frac{AM}{MB}=\frac{1}{2}$.
Найти $CM$ .
- Решение: По свойству аддитивности отрезка $AM + MB = 9$ , по условию $\frac{AM}{MB}=\frac{1}{2}$ $\Rightarrow$ $AM = 3$ , $MB = 6$
- Из прямоугольного $\bigtriangleup ABC$ по определению косинуса угла: $\cos B=\frac{BC}{AB}=\frac{3}{9}=\frac{1}{3}$ .
- Из $\bigtriangleup CMB$ по теореме косинусов найдем $CM$ : $CM^2=CB^2+MB^2-2\cdot CB\cdot MB\cdot\cos B$ , подставим числа
- $CM^2=3^2+6^2-2\cdot3\cdot6\cdot\frac{1}{3}=33$ $\Rightarrow$ требуемый отрезок $CM=\sqrt{33}$ . Ответ: $CM=\sqrt{33}$
Задача 5: Одна из сторон треугольника больше другой на $8$ см, а угол между ними $120^o$ .
Найдите периметр треугольника, если длина третьей стороны $28$ см .
- Решение: Метод введения неизвестного: Обозначим одну из сторон треугольника как $x$ ,
- выразим нужные величины через х и составим уравнение: величина другой стороны будет равна $x+8$ см.
- По теореме косинусов: $28^2=x^2+\left(x+8\right)^2-2x\cdot\left(x+8\right)\cdot\cos120$ , где $\cos120=\cos\left(180-60\right)=-\cos\left(60\right)=-0,5$,
- Итак, составили уравнение $784=x^2+x^2+16x+64-2x\left(x+8\right)\left(-0,5\right)$ $\Rightarrow$ $3x^2+24x+720=0$
- решим квадратное уравнение : один корень отрицательный - не нужен , другой $x=\frac{-24+96}{6}=12$
- Периметр $P=12+\left(12+8\right)+28=60$. Ответ: $60$.
Задача 6: В $\bigtriangleup ABC$ известны стороны $a=15$ , $b=18$, $c=25$ . Найти: углы $α$, $β$, $γ$ (приближённо) .
- Решение: Углы $α$ и $β$ найдём по теореме косинусов для соответствующих углов.
- $\cos\alpha=\frac{b^2+c^2-a^2}{2bc}$ , вычисляем $\cos\alpha=\frac{18^2+25^2-15^2}{2\cdot18\cdot25}\approx0,8$ , привлекаем калькулятор: $\alpha\approx36,4^o$ ;
- $\cos\beta=\frac{a^2+c^2-b^2}{2ac}$ , вычисляем $\cos\beta=\frac{15^2+25^2-18^2}{2\cdot15\cdot25}\approx0,7$ , .... калькулятор: $\beta\approx45,3^o$ .
- Найдём $γ$ по теореме о 180 = сумма углов: $\gamma=180-\left(\alpha+\beta\right)$ и $\gamma\approx180-\left(36,4+45,3\right)\approx98,3$ .
- Ответ: $\alpha\approx36,4^o$ , $\beta\approx45,3^o$ , $\gamma\approx98,3$


Задача 7: В $\bigtriangleup ABC$ $AB=c=3$ м, $AC = b = 6$ м. , $\alpha=60$ . Найти: сторону $a = BC$ , углы $β$, $γ$ .
- Решение: Треугольник задан двумя сторонами и углом между ними, следовательно, он задан полностью.
- По теореме косинусов $a^2=b^2+c^2-2bc\cdot\cos\alpha$ найдём сторону $a$:
- $a^2=6^2+3^2-2\cdot6\cdot3\cdot\cos60=36+9-36\cdot\frac{1}{2}=27$ $\Rightarrow$ $a=3\sqrt{3}$ .
- По теореме косинусов найдем и угол $β$ : $\cos\beta=\frac{a^2+c^2-b^2}{2ac}$ , $\cos\beta=\frac{27+9-36}{18\sqrt{3}}=0$ $\Rightarrow$ $β=90$ .
- Значит $\bigtriangleup ABC$ - прямоугольный , тогда угол $γ=90-α$ . Ответ: $a=3\sqrt{3}$ , $β = 90$ , $γ=30$ .
Задача 8: Стороны треугольника равны $11$ , $12$ и $13$ . Найти биссектрису, проведенную к стороне, равной 12.
- дано: $AB=11$ , $BC=12$ , $AC=13$ Найти биссектрису $AK=?$ .
- Решение: Найдем косинус угла из теоремы косинусов : $AB^2=AC^2+BC^2-2\cdot AC\cdot BC\cdot\cos \angle ACB$
- Выразим косинус $\cos \angle ACB=\frac{AC^2+BC^2-AB^2}{2\cdot AC\cdot BC}$ , $\cos \angle ACB=\frac{13^2+12^2-11^2}{2\cdot 13\cdot 12}=\frac{19}{39}$
- Найдем отрезки $BK$ , $KC$ на которые биссектриса делит сторону ... по теореме биссектрис $\frac{BK}{KC}=\frac{AB}{AC}$
- Система уравнений: $\frac{BK}{KC}=\frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем $BK=5,5$ , $BK=6,5$
- Теперь, для нахождения биссектрисы $AK$ еще раз используем теорему косинусов для треугольника $\bigtriangleup AKC$
- $AK^2=AC^2+KC^2-2\cdot AC\cdot KC\cdot\cos \angle ACB$ подставим значения $AK^2=13^2+6,5^2-2\cdot 13\cdot 6,5\cdot \frac{11}{13}=\frac{429}{4}$.
- Ответ: $AK=\frac{\sqrt429}{2}$.
Задача 9: Стороны треугольника равны $11$ , $12$ и $13$ . Найти медиану, проведенную к большей стороне.
- Решение: Воспользуемся формулой для длины медианы: $m_c=\frac{1}{2}\sqrt{2a^2+2b^2-c^2}$
- Подставим значения $m_c=\frac{1}{2}\sqrt{2\cdot11^2+2\cdot12^2-13^2}=\frac{1}{2}\sqrt{242+288-169}=\frac{1}{2}\sqrt{361}=\frac{19}{2}=9,5$ Ответ: $m_c=9,5$
Задача 10: В треугольнике $ABC$ $AB=11$ , $AC=23$ , медиана $AK=10$ . Найти $BC$ .
- Решение: Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
- $AK=\frac{1}{2}\sqrt{2\cdot11^2+2\cdot23^2-BC}$ $\Rightarrow$ $100=\frac{1}{4}\left(242+1058-BC^2\right)$ $\Rightarrow$ $BC^2=900$ Ответ: $BC=30$ .
Упражнения (А):
Упражнения (В):

