Простейшие уравнения с радикалами
Правило возведения в квадрат обеих частей уравнения::
если $A=B$ , тогда $A^2=B^2$ , но не наоборот: ($A^2=B^2$ не $\Leftrightarrow$ $A=B$ ) .
$A^2=B^2$ $\Rightarrow $ $A=B$ при условии: $A$ и $B$ одного и того же знака.
$\sqrt{X}=C$ $\Rightarrow $ $X=C^2$ при условии: $C\ge0$ , $C$ - неотрицательна.
Пример 1: Решить уравнение $\sqrt{\frac{3+12x}{2x-1}}=3$
- Вопрос к уравнению: каким числом должно быть неизвестное $x$ , чтобы стать корнем уравнения ,
- т.е. чтобы уравнять собой левую и правую части ? не знаем каким числом в будущем окажется $x$ ,
- но сейчас , очевидно , дробь $\frac{3+12x}{2x-1}$ должна равняться $9$ . а как иначе левое станет $3$? никак.
- вывод: чтобы сравнялись части, нужно, чтобы сравнялись их квадраты . $A=B$ $\Rightarrow$ $A^2=B^2$ .
- метод решения - избавление от радикала - возведение обеих частей в квадрат: формула $\left(\sqrt{A}\right)^2=A$ - .
- применим этот метод и возведем обе части в квадрат $\left(\sqrt{\frac{3+12x}{2x-1}}\right)^2=\left(3\right)^2$ $\Leftrightarrow$ - так избавимся от радикала
- $\frac{3+12x}{2x-1}=9$ и получим "простое" без радикалов уравнение $3+12x=9\cdot\left(2x-1\right)$ $\Leftrightarrow$ $12=18x-12x$ ,
- наконец-то найдем то самое число , каким должно быть неизвестное ответ: $x=2$
Пример 2: Решить уравнение $\sqrt{6-4x-x^2}=-3-2x $
- В начале уточним некоторые детали. не знаем каким станет выравнивающий обе части $x$ , но в любом случае:
- под радикалом должно быть неотрицательное значение. иначе получится "ложь" - бессмыслица.
- надо указать ОДЗ - ограничение $6-4x-x^2\ge0$ : (допустимо!) все, что под радикалом $\ge0$.
- избавимся от радикала одновременным возведением обеих частей в квадрат.
- но это не гарантирует "уравнивания до возведения" . (Может было 4 = -4 , стало 16 = 16)
- бывает такое: после возведения в квадрат части уравниваются, хотя до операции они были не равны .
- например: $\left(-3\right)^2=\left(3\right)^2$ , но ведь $-3\ne3$ .
- нам нужны гарантии , что равные после возведения в квадрат части $A^2=B^2$ , были бы равными и до
- такое возможно только при условии : обе части уравнения до возведения $A$ и $B$ должны быть одного знака.
- $\left(\sqrt{6-4x-x^2}\right)^2=\left(-3-2x\right)^2$ при условии $-3-2x\ge0$ (правая часть до возведения должна быть $\ge0$ )
- оговорка при условии гарантирует одинаковость знаков частей "до" операции возведения в квадрат :
- левая часть - это радикал , он неотрицателен $\Rightarrow$ значит правая часть уравнения неотрицательна.
- используем формулы: $\left(\sqrt{a}\right)^2=a$ ; $\left(a+b\right)^2=a^2+2ab+b^2$ получим $6-4x-x^2=9+12x+4x^2$
- решим квадратное уравнение $5x^2+16x+3=0$. два корня $x=-3$ , $x=-0.2$ .
- внимание: корни должны пройти ОДЗ и при условии. Если какой-то не проходят, значит этот корень ложный.
- проверка: $x=-3$ 1) ОДЗ - да!. 2) "при" $-3-2x\ge0$ - да! $\Rightarrow$ истинное решение.
- проверка: $x=-0.2$ $\Rightarrow$ 1) ОДЗ - да!. 2) "при" $-3-2x\ge0$ - нет! $\Rightarrow$ ложное решение.
- ответ: $x=-3$ в ответе перечисляем только истинные, уравнивающие решения.
Область Допустимых Значений - ОДЗ - ОДЗ выражения, ОДЗ уравнения
- те числовые значения переменной, при которых выражения имеют смысл ... вычисляются.
- но не те числа, при которых выражение невозможно вычислить
- ОДЗ уравнения - те числовые значения неизвестного, при которых выполняется ОДЗ каждого выражения.
- У выражения с квадратным радикалом ОДЗ условие: под радикальное выражение неотрицательно.
- Если в уравнении есть радикалы, то условия ОДЗ: Каждое подрадикальное $\ge0$. (под корнем минусовое нельзя)
- Если есть дробь, то условия ОДЗ: каждый знаменатель $\ne0$. (делить на 0 нельзя!)
 белы
белы 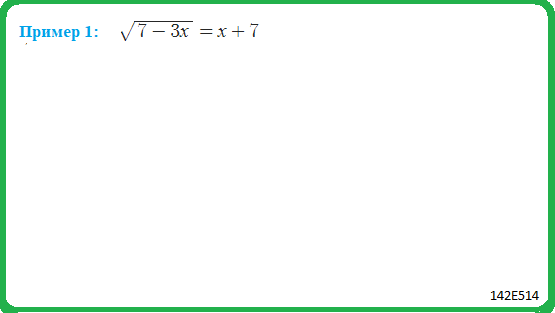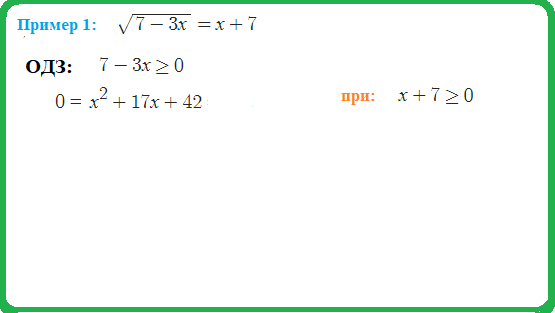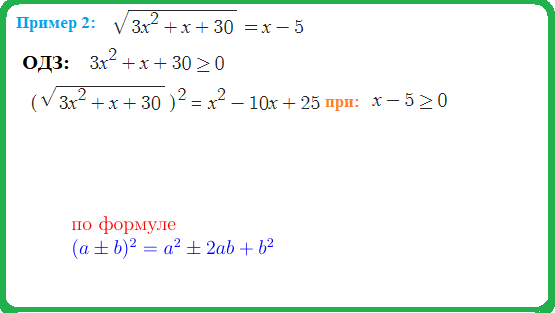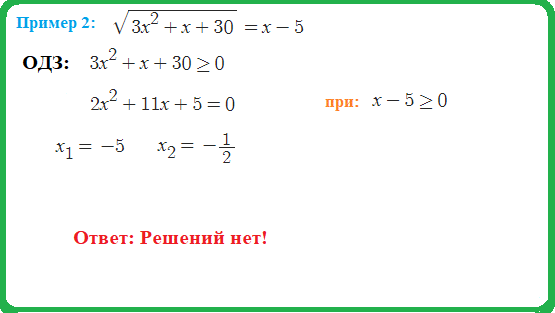
Один радикал в уравнении
Напоминание: Избавиться от радикала в уравнении $\sqrt{A}=B$ можно путем возведения его в квадрат $\left(\sqrt{ }\right)^2$ , для этого радикал должен быть уединенным в одной из частей уравнения $\sqrt{A}$. "При условии" относится к противоположной от радикала части уравнения - выражению $B$ и накладывается до возведения в квадрат, но пишется при возведении $\left(B\right)^2$
Пример 3: Решить уравнение $\sqrt{5-x^2}-2x=3-x$
- вопросы: как нам из этого уравнения получить такое, какое мы уже научились решать? как нам прийти к виду "радикал равняется не радикальному выражению" ?
- NB: "правильно поставленный вопрос уже полдела. все открытия начинаются от хорошего вопроса. ставьте вопросы! "
- ОДЗ $5-x^2\ge0$ $\Leftrightarrow $ условие ОДЗ гарантирует "не ложность" решения. перенесем все нерадикальные
- слагаемые на противоположную от радикала сторону $ \sqrt{5-x^2}=2x+3-x$ - так мы уединяем радикал.
- возведение обеих частей в квадрат и "при условии" : $\left(\sqrt{5-x^2}\right)^2=\left(x+3\right)^2$ при $x+3\ge0$
- далее, $5-x^2=x^2+6x+9$ $\Leftrightarrow$ $2x^2+6x+4=0$ $\Leftrightarrow$ $x^2+3x+2=0$ $\Rightarrow$ корни $x=-1$ , $x=-2$
- ответ: $x=-1$ , $x=-2$ оба корня истинные, т.к. проходят ОДЗ и "при условии".
Равенство радикалов
Пример 4: Решить уравнение $\sqrt{2-x+x^2}-\sqrt{6-2x}=0$
- ОДЗ: $2-x+x^2\ge0$ ; $6-2x\ge0$ - условие допустимости к решению : определяем когда радикалы существуют.
- перенесем один из радикалов направо, тем самым сравняем радикалы и подготовим возведение в квадрат обеих частей,
- $\sqrt{2-x+x^2}=\sqrt{6-2x}$ . "при условии" писать не будем , ведь обе части уже $\ge0$ из-за радикалов, см. ОДЗ.
дальнейшая стратегия:
1. избавимся от радикалов: возведем обе части в квадрат. условия не нужны, радикалы одного знака.
2. решим полученное нерадикальное уравнение.
3. Проверим решения на выполнимость всех ОДЗ ограничений. забракуем ложные корни.
 белы
белы 
Интерактивная Доска:
Упражнения:
