Свойства числовых неравенств:
Свойство 1: если $a > b$ и $b > c$ $\Rightarrow$ $a > c$ свойство транзитивности;
Свойство 2: если $a > b$ $\Rightarrow$ $a+c > b+c$ добавление слагаемого к обеим частям не меняет знак неравенства;
это свойство позволяет выполнить операцию "перенос слагаемого".
Свойство 3: если $a > b$ и множитель $m > 0$ $\Rightarrow$ $am > bm$,
после умножения неравенства на положительное число, знак неравенства не меняется.
если $a > b$ и $m < 0$ $\Rightarrow$ $am < bm$ ,
после умножения неравенства на отрицательное число, знак неравенства меняется.
Свойство 4: если $a > b$ и $c > d$ $\Rightarrow$ $a+c > b+d$ одноименные неравенства можно почленно складывать.
Свойство 5: если $a$, $b$, $c$, $d$ - положительные числа и $a > b$, $c > d$, $\Rightarrow$ $a\cdot c > b\cdot d$
одноименные неравенства можно почленно умножать.
Свойство 6: если $a$ и $b$ - неотрицательные числа и $a > b$ $\Rightarrow$ $a^n > b^n$, где $n$ - любое натуральное число
при возведении в натуральную степень знак неравенства не меняется.

Сравнение чисел:
Пример 1: Сравнить числа $0,1\cdot0,77\cdot0,121$ и $2,5\cdot \frac{5,6\cdot 10^{-7}}{2,1\cdot 10^{-5}}$
- Стратегия "как сравнить два числовых выражений": предположим, что первое меньше второго ,
- затем по свойствам числовых неравенств преобразуем нашу гипотезу до "очевидного".
- Если придем к верному неравенству, значит наше предположение оправдалось , ....
- .... в противном случае, исходное неравенство выполняется "ровно наоборот".
- "Сравнить числа" = составить с ними неравенство, которое нужно доказать или опровергнуть.
- "рабочая гипотеза": $0,1\cdot0.77\cdot0.121 < 2,5\cdot\frac{5,6\cdot10^{-7}}{2,1\cdot10^{-5}}$
- эквивалентные преобразования числового неравенства : $\frac{7}{100000}\cdot11\cdot121 < 5\cdot\frac{8}{3}\cdot\frac{1}{100}$ $\Leftrightarrow$
- $\frac{7}{100000}\cdot11\cdot121 < \frac{20}{3}\cdot\frac{1}{100}$ $\Leftrightarrow$ $7\cdot1331\cdot3 < 2\cdot10000$ $\Leftrightarrow$ $27951 < 20000$ , что "очевидно неверно" ,
- значит $\Rightarrow$ $0,7\cdot0.77\cdot0.777 > 2,5\cdot\frac{5,6\cdot10^{-7}}{2,1\cdot10^{-5}}$
Пример 2: Расположить по убыванию числа $a-1$ ; $2+a$ ; $-a^2$ ; $-\frac{1}{a}$ , если число $a$ из интервала $-3 < a < -2$.
- Возьмем из интервала приближенное $a\approx-2,4$ . посмотрим, чему будет равно каждое из выражений:
- $a-1\approx-2,4-1\approx-3,4$ ; $2+a\approx-0,4$ ; $-a^2\approx-5,76$ ; $-\frac{1}{a}\approx0,41$
- сравним получившиеся значения и выстроим убывающую последовательность.
- Ответ : $-\frac{1}{a}>2+a>a-1>-a^2$
Сравнение радикальных чисел
Пример 3 : Между какими соседними целыми находится число с радикалом, приближенные значения
- $\sqrt{7} ?$ Т.к $2^2=4$ меньше $<7<$ меньше $3^2=9$ , то Ответ: $2<\sqrt{7}<3$
- $\sqrt{34} ?$ Т.к $5^2=25$ меньше $<34<$ меньше $6^2=36$ , то Ответ: $5<\sqrt{34}<6$
- $\sqrt{407} ?$ Т.к $20^2=400$ меньше $<407<$ $21^2=441$ , то Ответ: $20<\sqrt{407}<21$
- Суть: Находим ближайший "квадрат чего либо" менее чем наше число. И чтоб квадрат "следующего" было больше ...
- $\sqrt{3}\approx ?$ Легче узнать приближенно $\sqrt{300}\approx 17$ и поделить на $10$. Ответ: $\sqrt{3}\approx 1,7$
- $\sqrt{17}\approx ?$ Легче узнать приближенно $\sqrt{1700}\approx 42$ и поделить на $10$. Ответ: $\sqrt{17}\approx 4,2$
- $3\sqrt{7}-\sqrt{11}\approx ?$ $\sqrt{7}\approx 2,7$ $\sqrt{11}\approx 3,3$ $3\cdot2,7-3,3=4,8$ Ответ: $3\sqrt{7}-\sqrt{11}\approx 4,8$
Сравнить, значит узнать что больше, что меньше. Что на числовой оси левее, а что правее - значит больше. Чтоб сравнить числа, иногда достаточно сравнить их приближенные значения ... станет ясно что больше. Иногда полезно сравнить их квадраты и, в зависимости от знаков, сделать выводы о сравнениях ... Иногда полезно оба сравниваемых числа умножить на один и тот же множитель, ( на $2$ ? $\sqrt{3}$ ? $100$ ?) и сравнить полученные числа
Пример 4 : Сравнить числа $\sqrt{26}$ и $5,1$
Сравнить числа $\sqrt{26}$ и $5,1$ ? Сравним квадраты этих положительных чисел - "чей квадрат больше, тот и больше" $\left(\sqrt{26}\right)^2=26$ $5,1^2=26,01$ вывод, Ответ: $\sqrt{26}<5,1$
Сравнить числа $\sqrt{5}-7$ и $-3-\sqrt{2}$ ? Вычислим приближенно число: $\sqrt{5}-7\approx 2,3-7=-4,7$ Вычислим приближенно число: $-3-\sqrt{2}\approx -3-1,4=-4,4$. Сравним приближенные значения: т.к. $-4,7<-4,4$ то делаем вывод, Ответ: $\sqrt{5}-7<-3-\sqrt{2}$
Сравнить числа $-4\sqrt{3}$ и $-3\sqrt{5}$ ? Сравним квадраты положительных чисел $4\sqrt{3}$ и $3\sqrt{5}$- "чей квадрат больше, тот и больше" . $\left(4\sqrt{3}\right)^2=48$ $(3\sqrt{5})^2=45$ вывод : Ответ: $4\sqrt{3}>3\sqrt{5}$ . .... Но их противоположные отрицательные наоборот: $-4\sqrt{3}<-3\sqrt{5}$ "Чем левее, тем меньше".
Пример 5: Сравнить числа $2\sqrt{11}$ и $3\sqrt{5}$
- "Сравнить числа" - значит доказать или опровергнуть составленное с ними неравенство.
- Предположим , что первое число больше второго. Это неравенство упростим до "наглядности":
- $2\sqrt{11} > 3\sqrt{5}$ $\Leftrightarrow$ $\left(2\sqrt{11}\right)^2 > \left(3\sqrt{5}\right)^2$ $\Leftrightarrow$ $4\cdot11 > 9\cdot5$ $\Leftrightarrow$ $44 > 45$ , это неверно ,
- а значит и наша неверна $\Rightarrow$ Ответ : $2\sqrt{11} < 3\sqrt{5}$
Правило сравнения:
- составить из сравниваемых чисел гипотетическое, предположительное неравенство;
- путем эквивалентных преобразований доказать его или опровергнуть ;
- если последнее неравенство в цепочке преобразований верно/ложно $\Leftrightarrow$ гипотетическое неравенство верно/ложно.
Пример 6: Сравнить числа $\frac{z^2}{8}-\frac{8}{z-4}$ и $\sqrt{z}$ при $z\approx7$.
- Найдем приближенное значение второго выражения $\sqrt{z}\approx\sqrt{7}\approx\sqrt{\frac{700}{100}}\approx\sqrt{\frac{729}{100}}\approx2,7$ и первого:
- $\frac{z^2}{8}-\frac{8}{z-4}\approx\frac{49}{8}-\frac{8}{3}\approx6,01-2,66\approx3,35$ $\Rightarrow$ видно, что первое больше второго.
- Ответ : $\frac{z^2}{8}-\frac{8}{z-4}>\sqrt{z}$
Пример 7: Сравнить числа $-\frac{9-\sqrt{12}}{4}$ и $-\frac{11}{8}$ .
- Допустим гипотезу $-\frac{9-\sqrt{12}}{4} > -\frac{11}{8}$ . Если бы это было верно, тогда :
- $\frac{9-\sqrt{12}}{4} < \frac{11}{8}$ $\Leftrightarrow$ $2\left(9-\sqrt{12}\right) < 11$ $\Leftrightarrow$ $18-11 < 2\sqrt{12}$ $\Leftrightarrow$ $7^2 < \left(2\sqrt{12}\right)^2$ $\Leftrightarrow$ $49 < 4\cdot12$ .
- Но! последнее очевидно ложно $\Rightarrow$ вывод: наше допущение надо поменять на противоположное $\Rightarrow$
- Ответ: $-\frac{9-\sqrt{12}}{4}$ < $-\frac{11}{8}$.
Пример 8: Сравнить числа $\frac{-3-\sqrt{17}}{3}$ и $8-3\cdot\sqrt{12}$ .
- Сделаем допущение $\frac{-3-\sqrt{17}}{3} < 8-3\cdot\sqrt{12}$ и проверим путем эквивалентных преобразований:
- $3\cdot\left(\frac{-3-\sqrt{17}}{3}\right) < 3\cdot\left(8-3\cdot\sqrt{12}\right)$ $\Leftrightarrow$ $-3-\sqrt{17} < 24-9\cdot\sqrt{12}$ $\Leftrightarrow$ $9\cdot\sqrt{12} < 27+\sqrt{17}$
- обе части неравенства положительные, значит, можем сравнить квадраты:
- $\Leftrightarrow$ $\left(9\cdot\sqrt{12}\right)^2 < \left(27+\sqrt{17}\right)^2$ $\Leftrightarrow$ $81\cdot12 < 27^2+2\cdot27\cdot\sqrt{17}+17$ $\Leftrightarrow$
- $972-729-17 < 54\sqrt{17}$ $\Leftrightarrow$ $260 < 54\sqrt{17}$ $\Leftrightarrow$ $130 < 27\sqrt{17}$ $\Leftrightarrow$ $\left(130\right)^2<\left(27\sqrt{17}\right)^2$ $\Leftrightarrow$
- $16900 < 729\cdot17$ $\Leftrightarrow$ $16900 < 12393$ - это "Ложь" и начальное неравенство берем ровно наоборот.
- Ответ: $\frac{-3-\sqrt{17}}{3}$ > $8-3\cdot\sqrt{12}$.
Выбор верных утверждений о неравенствах по картинкам, рисункам, графикам:
Пример 9: На числовых осях отмечены точки с буквами. Каковы числовые значения этих букв, если известно, что они выбраны из списка чисел, указанных на картинках у числовых осей.
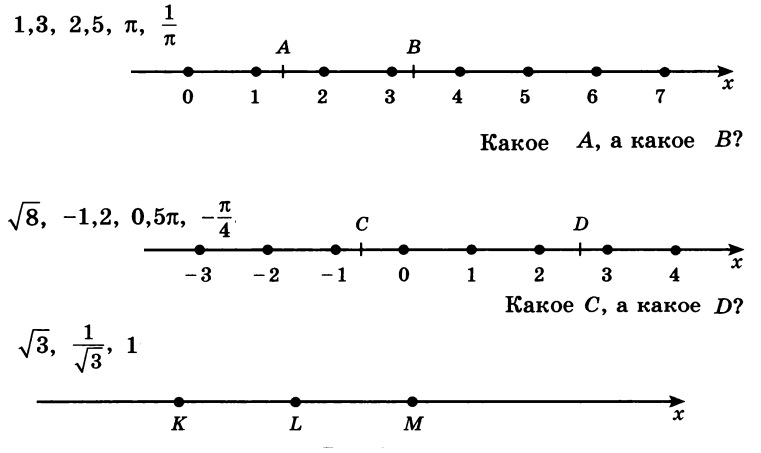
- Видно, что число $A$ находится между $1$ и $2$. Какое из предложенных чисел попадает туда же?
- Точка $С$ левее нуля, ближе к $-1$. Какое число могло быть там?
- $K$ - самое меньшее, $L$ среднее, $M$ - правое. А как с порядком предложенных чисел?
Интерактивная Доска:
Упражнения:
