Рациональные уравнения: применение формул

Учебник
Алгебра, 9 класс
IMG_0454.JPG

Учитель

Темур Кварацхелия
Рациональные уравнения: применение формул

                                                                                            Формулы сокращенного умножения:

$\left(a\pm b\right)^2=a^2\pm2ab+b^2$                             $a^2-b^2=\left(a-b\right)\left(a+b\right)$

$\left(a\pm b\right)^3=a^3\pm3a^2b+3ab^2\pm b^3$           $a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)$          $a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)$

$a^4-b^4=\left(a^2-b^2\right)\left(a^2+b^2\right)=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)$

$\left(a\pm b\right)^2=a^2\pm2ab+b^2$
$a^2-b^2=\left(a-b\right)\left(a+b\right)$

$\left(a\pm b\right)^3=a^3\pm3a^2b+3ab^2\pm b^3$
$a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)$
$a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)$
$a^4-b^4=\left(a^2-b^2\right)\left(a^2+b^2\right)=$
$=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)$


Пример 1:                  Разложить многочлены на множители                  

  • $12x^2-18x=$      вынос за скобки      $=6\cdot x\cdot\left(2x-3\right)$
  • $1-16z^2=$    разность квадратов    $=\left(1-4z\right)\left(1+4z\right)$
  • $2x^2+5x+3=$         теорема Виета    $=2\cdot\left(x+1\right)\cdot\left(x+\frac{3}{2}\right)=$     упростим вид     $=\left(x+1\right)\cdot\left(2x+3\right)$
  • $-4+20a-25a^2=$    "минус"   сумма,   разность   в   квадрате     $=-\left(2-5a\right)^2$
  • $8x^3+27=$     сумма,   разность   кубов     $=\left(2x+3\right)\left(4x^2-6x+9\right)$
  • $27x^3-27x^2+9x-1=$     сумма,   разность   в   кубе    $=\left(3x-1\right)^3$
  • $625-x^4=$     разность квадратов    $=\left(25-x^2\right)\left(25+x^2\right)=$    еще раз разность квадратов     $=\left(5-x\right)\left(5+x\right)\left(25+x^2\right)$
  • $x^3-7x^2+4x-28=$     попарно,   вынос за скобки    $=x^2\left(x-7\right)+4\left(x-7\right)=$    вынос общего     $=\left(x-7\right)\left(x^2+4\right)$
  • $x^3-16x=$     вынос множителя,      $=x\left(x^2-16\right)=$     разложение разности квадратов     $=x\left(x-4\right)\left(x+4\right)$


                 Формулы сокращенного сложения алгебраических дробей, НОК знаменателей:

$\frac{a}{b\cdot M}-\frac{c}{d\cdot M}=\frac{a\cdot d-c\cdot b}{b\cdot d\cdot M}$                              $\frac{a}{b\cdot M}+\frac{c}{d\cdot M}=\frac{a\cdot d+c\cdot b}{b\cdot d\cdot M}$

$\frac{x}{M}-\frac{y}{z\cdot M}=\frac{x\cdot z-y\cdot1}{z\cdot M}$                               $\frac{x}{M}+\frac{y}{z\cdot M}=\frac{x\cdot z+y\cdot1}{z\cdot M}$                        

         

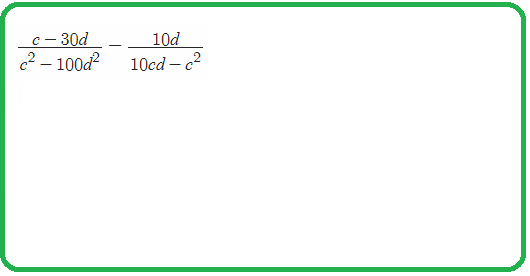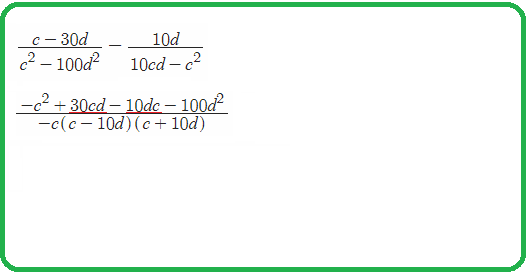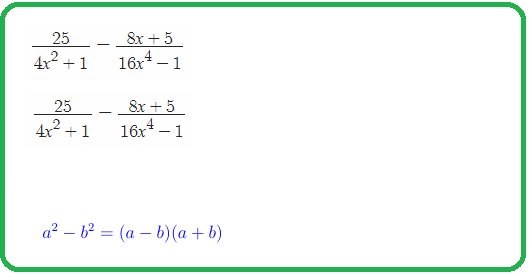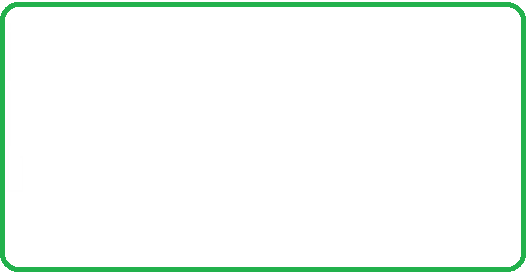
Пример 2:                  Решить уравнение              $\frac{4}{x+2}+3=\frac{3x^2-8}{x^2-4}$             

  • знаменатель   разложим    на множители       $x^2-4=\left(x-2\right)\left(x+2\right)$ ,    множитель    $x+2$    есть в 1-ом знаменателе
  • перенесем все слагаемые из правой части в левую и приведем их к общему знаменателю,      $\frac{4}{x+2}+3-\frac{3x^2-8}{x^2-4}=0$       $\Leftrightarrow$       
  • $\frac{4\left(x-2\right)+3\left(x^2-4\right)-\left(3x^2-8\right)}{\left(x-2\right)\left(x+2\right)}=0$        $\Leftrightarrow$        $\frac{4x-8+3x^2-12-3x^2+8}{\left(x-2\right)\left(x+2\right)}=0$        $\Leftrightarrow$            $\frac{4x-12}{\left(x-2\right)\left(x+2\right)}=0$         "дробь   =   $0$"     ,
  • числитель приравняем к нулю       $4x-12=0$            при       $\left(x-2\right)\left(x+2\right)\ne0$          $\Leftrightarrow$             Ответ:     $x=3$

Пример 3:                  Решить уравнение              $\frac{x^2-2x+4}{x^3-2x^2+4x-8}+\frac{x^2+2x+4}{x^3+2x^2+4x+8}=\frac{2x+2}{x^2-4}$

  • разложим на множители         $x^3-2x^2+4x-8=x^2\left(x-2\right)+4\left(x-2\right)=\left(x-2\right)\left(x^2+4\right)$ ,
  • $x^3+2x^2+4x+8=x^2\left(x+2\right)+4\left(x+2\right)=\left(x+2\right)\left(x^2+4\right)$ ,      по формуле        $x^2-4=\left(x-2\right)\left(x+2\right)$
  • Leftrightarrow$         заменим знаменатели на разложения          $\frac{x^2-2x+4}{\left(x-2\right)\left(x^2+4\right)}+\frac{x^2+2x+4}{\left(x+2\right)\left(x^2+4\right)}=\frac{2x+2}{\left(x-2\right)\left(x+2\right)}$ ,    сложим дроби,
  • НОК   знаменателей        $\frac{\left(x^2-2x+4\right)\left(x+2\right)+\left(x^2+2x+4\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)\left(x^2+4\right)}=\frac{2x+2}{\left(x-2\right)\left(x+2\right)}$ ,          упростим числитель,   откроем скобки,
  • формулы   кубов,              $\frac{x^3-8+x^3+8}{\left(x+2\right)\left(x-2\right)\left(x^2+4\right)}=\frac{2x+2}{\left(x-2\right)\left(x+2\right)}$        $\Leftrightarrow$           $\frac{2x^3}{\left(x+2\right)\left(x-2\right)\left(x^2+4\right)}=\frac{2x+2}{\left(x-2\right)\left(x+2\right)}$    ,     умножим
  • обе части уравнения на общий знаменатель    $\left(x+2\right)\left(x-2\right)\left(x^2+4\right)$ ,    сократим на   $2$       $\Leftrightarrow$      $x^3=\left(x+1\right)\left(x^2+4\right)$
  • $\Leftrightarrow$       $x^3=x^3+x^2+4x+4$       $\Leftrightarrow$       $x^2+4x+4=0$       $\Leftrightarrow$      $x=-2$ ,   но это решение не удовлетворяет уравнение,
  • т.к. не удовлетворяет     одно из    ОДЗ         $x^2-4\ne0$   .                    Ответ:       решений    нет.

Пример 4:                  Решить уравнение              $\frac{1}{x+3}-\frac{x^3}{x^4-81}=\frac{21}{x^3+3x^2+9x+27}$          

  • для успешного,   сокращенного сложения дробей,   разложим знаменатели на множители. по формулам сокращенного умножения
  • знаменатель     $x^4-81$    можно разложить так:          $x^4-81=\left(x^2-9\right)\left(x^2+9\right)=\left(x+3\right)\left(x-3\right)\left(x^2+9\right)$
  • $\Leftrightarrow$        $\frac{1}{x+3}-\frac{x^3}{\left(x+3\right)\left(x-3\right)\left(x^2+9\right)}=\frac{21}{x^3+3x^2+9x+27}$ ,         сложим дроби,   учитывая общий    множитель     $x+3$    в обеих частях
  • $\frac{-3x^2+9x-27}{\left(x+3\right)\left(x-3\right)\left(x^2+9\right)}=\frac{21}{x^3+3x^2+9x+27}$            вернем прежний знаменатель          $\frac{-3x^2+9x-27}{x^4-81}-\frac{21}{x^3+3x^2+9x+27}=0$       и     разложим
  • на множители по другому       $x^4-81=\left(x-3\right)\left(x^3+3x^2+9x+27\right)$ ,    получим общий множитель со второй дробью
  • $\frac{-3x^2+9x-27}{\left(x-3\right)\left(x^3+3x^2+9x+27\right)}-\frac{21}{x^3+3x^2+9x+27}=0$ ,           сложим дроби   "по сокращенному"      $\frac{a}{b\cdot z}-\frac{c}{z}=\frac{a\cdot1-c\cdot b}{b\cdot z}$
  • $\Leftrightarrow$           $\frac{\left(-3x^2+9x-27\right)\cdot1-21\cdot\left(x-3\right)}{\left(x-3\right)\left(x^3+3x^2+9x+27\right)}=0$   ,                упростим числитель        $\frac{-3x^2-12x+36}{\left(x-3\right)\left(x^3+3x^2+9x+27\right)}=0$        $\Leftrightarrow$        "дробь   =   $0$"
  • $\Leftrightarrow$      $3x^2+12x-36=0$        $\Leftrightarrow$       $x^2+4x-12=0$              $\Leftrightarrow$                      Ответ:    $x_1=2$ ,   $x_2=-6$ .

         

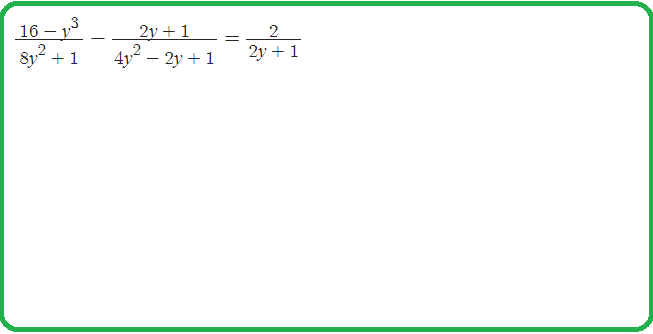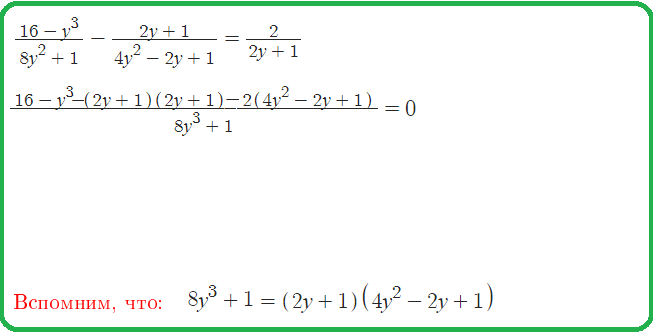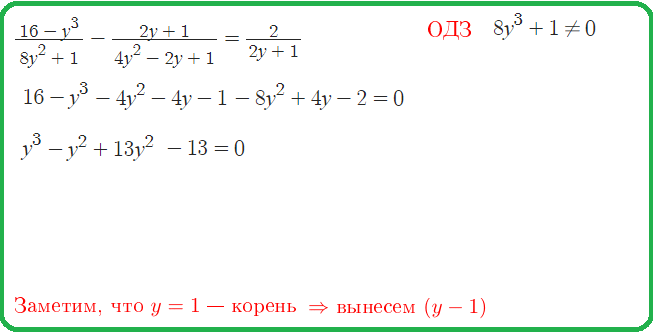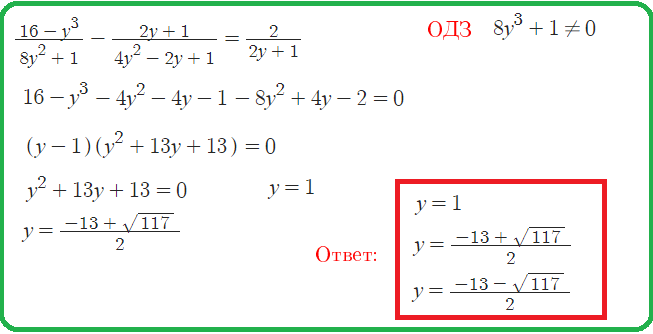
Интерактивная Доска:

Упражнения: