Парабола: график квадратичной функции

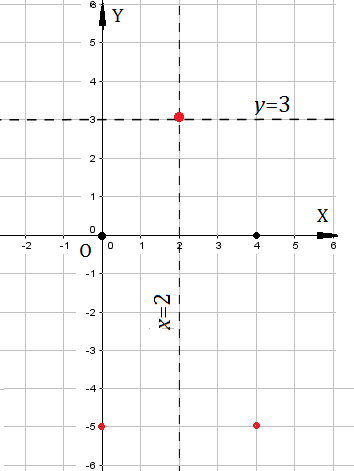
прямоугольная система координат    положение точки определяется двумя её координатами - абсциссой и ординатой .

Квадратичная   функция     $y=ax^2+bx+c$. Ее график - Парабола   

Алгоритм:    детальное построение   графика   заданной   функции

• вычислить значения функции:   различные   $x$   -   числа подставить в выражение функции и   найти   свои     $y$   -   значения.
• составить таблицу: список точек     ($x$; $y$ ),    пары соответствующих   $x$   - чисел и его   $y$   -    значений абсциссы и ординаты.
• нанести    эти   точки   из   списка   на   координатную   плоскость   в   соответствии   с   координатами   точек.
• построить график: кривую линию, параболу,   проходящую через   все   нанесенные     точки.    Аккуратно, красиво!
• при необходимости,    дополнить список новыми точками:    подобрать    $x$   -   числа   для   коррекции,   уточнения   графика.

    

Функции   $y=ax^2$,      $y=ax^2+с$ .     Парабола.   Свойства.

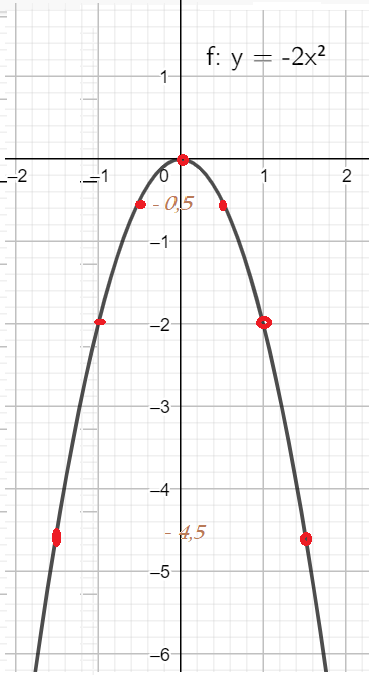
Пример 1:          Построить   график   для   функции   $y=-3x^2$

• Вычислим   значения   функции   в   разнознаковых   точках. Нанесем точки (с координатами) в системе   $XOY$.
• $x=1$           $f\left(1\right)=-3$                $x=\frac{1}{2}$           $f\left(\frac{1}{2}\right)=-0,75$               $x=-1$           $f\left(-1\right)=-3$               $f\left(-\frac{1}{2}\right)=-0,75$
• $x=2$           $f\left(2\right)=-12$                $x=1,5$           $f\left(1,5\right)=-6,75$                             $x=-1,5$           $f\left(-1,5\right)=-6,75$
• $x=0$           $f\left(0\right)=0$                $x=2,5$           $f\left(2,5\right)=-18,75$               $x=-2,5$           $f\left(-2,5\right)=-18,75$                     .
• В $XOY$   укажем   точки   $(0;0)$,   $(1;1)$,   $(2;12)$,   $(1/2;-0,75)$,   $(1/2;-0,75)$,   $(1,5;-6,75)$,   $(-1,5;6,75)$,
• Еще точки:   $(-2;-12)$,   $(-2,5;-18,75)$,    $(2,5;-18,75)$, . По всем   точкам построим   график    $y=-3x^2$
• "Чтение" графика: Ветви параболы направленны вниз; Пересекает $y$ - ось в точке    $(0;0)$;    Симметрична по $y$ - оси.
• Корни функции: график пересекает    $x$ - ось   аргументе     $x=0$. Корень уравнения   $-3x^2=0$    $\Rightarrow$    $x=0$.
• $y=0$ - наибольшее значение среди всевозможных значений функции   $y=-3x^2$. Остальные - все отрицательные.

                              

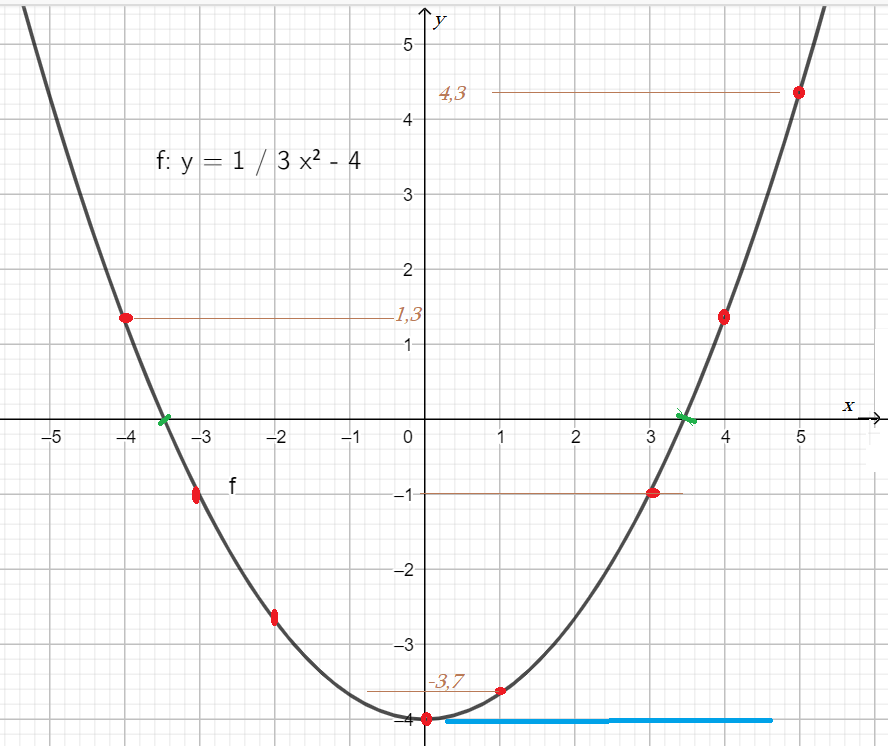
Пример 2:          Построить   график   для   функции     $y=\frac{1}{3}x^2-4$

• Вычислим   значения   функции    при нескольких аргументах    и   нанесем точки с координатами в системе   $XOY$.
• при $x=2$      $\Rightarrow$     $y=\frac{1}{3}\cdot2^2-4=\frac{4}{3}-4\approx1,3-4\approx-2,7$          $f\left(2\right)\approx -2,7$ . Получим точку      $(2;-2,7)$
• Замечание: для построения графика нам достаточно приближенные значения в виде десятичных чисел ...
• $f\left(1\right)\approx -3,7$ ;        $f\left(0\right)=-4$ ;        $f\left(-1\right)\approx -3,7$ ;             $f\left(-3\right)=-1$ ;     $f\left(4\right)\approx 1,3$ ;     $f\left(-5\right)\approx 4,3$ ;      $f\left(6\right)=8$
• В $XOY$   нанесем   точки   $(0;-4)$,   $(-1;-3,7)$,   $(2;2,7)$,   $(-3;-1)$,   $(4;1.3)$,   $(-5;4,3)$,   $(6;8)$,
  
• Еще точки:   $(3;-1)$,   $(-4;1.3)$,   $(5;4,3)$,   $(-6;8)$, . По всем этим точкам проходит график   функции   $y=\frac{1}{3}x^2-4$
• "Чтение" графика:   Ветви направленны вверх; Пересекает $y$ - ось в точке    $(0;-4)$;   Симметрична по $y$ - оси.
• Корни функции: график пересекает    $x$ - ось при аргументах     $x\approx -3,5$   и    $x\approx 3,5$.
• $y=-4$ - наименьшее значение функции   $y=-3x^2$. Она принимает значения из интервала    $( -4 ; + ∞)$

Все   свойства   графика   квадратичной   функции    $y=ax^2+bx+c$.    Чтение   графика:   Знаки   коэффициентов,   дискриминанта.   

Парабола      представляет   квадратичную   функцию.   Значит,   по виду   параболы   можно   многое   сказать о     $a$,   $b$,    $c$,   $D$,   $f(0)$.   Так,   если $a$   -   коэффициент квадратичной функции отрицателен,   то при больших     $x$    вычисление функции дает очень большое   отрицательное   значение.   это   значит,   что парабола   далеко   внизу,   ветвь   направлена   вниз.   а   как   иначе?                Если у   квадратичной   функции   есть   корень,   например,    $-4$    то   парабола   ведь   обязана   проходить   в   точке    ( -4 ; 0) ?   Т.е. корни указывают места прохождения параболы через Х - ось. Ну а если корней вообще нет, то парабола вовсе не пересекает Х - ось. Тогда она полностью внизу?       Ну а где парабола пересекает У - ось? там х = 0, значит, значение $f(0)=c$ определит точку.

1.   Знак    $a$   -   коэффициента    связан   с   направлением   ветвей   параболы:     

• $a > 0$     $\Leftrightarrow$     ветви параболы вверх.             Потому что при очень больших    $x=1000$ ,    значение    $y=+$     большое число.
• $a < 0$     $\Leftrightarrow$     ветви параболы вниз.             Так как   при больших     $x=1000$     значение     $y=-$     отрицательное число. Вычисли!
  

2.   Знак   $D$   -   дискриминанта связан с количеством пересечений параболы с осью   $x$   -   абсцисс.    Сколько раз пересекает?

• $D > 0$      уравнение   $ax^2+bx+c=0$    должно иметь $2$   корня,    значит парабола пересекает   $Х$ - абсциссу    $2$   раза .
• $D < 0$      уравнение   $ax^2+bx+c=0$     не имеет корней,   а это значит что парабола не пересекает    $Х$ - абсциссу.
• $D = 0$      уравнение   $ax^2+bx+c=0$    имеет $1$   корень.    парабола касается с   $Х$ - абсциссой. Парабола лежит на   $х$ - оси.

3.    Знак    $c$   - коэффициента   связан   со   значением   функции   при    $x = 0$.    То есть   пересечением   параболы с    $у$ - осью.

• при   $x=0$   значение    $y=a\cdot0^2+b\cdot0+c=c$.    парабола пересекает ординату "на высоте"    $y\left(0\right)=c$, в точке      $\left(0;c\right)$
• $c > 0$     тогда    $y\left(0\right) > 0$,    парабола   пересекает   ординату   в верхней части.
• $c < 0$     тогда    $y\left(0\right) < 0$,    парабола   пересекает   ординату   в   нижней   части.

4.   Ось симметрии параболы проходит вертикально через вершину параболы.   Знак    b - коэффициента ?

• Ось симметрии параболы:   линия      $x=-\frac{b}{2a}$ .      Вершина параболы находится при    $x=-\frac{b}{2a}$.   Там $min/ max$ !
• Пик находится при    $х$   - координате   $x=-\frac{b}{2a}$      ровно по середине между   $x_1$   и   $x_2$   корнями :     $-\frac{b}{2a}=\frac{x_1+x_2}{2}$.
• Ось параболы правее   $у$   -   ординаты     $\Leftrightarrow$      $-\frac{b}{2a} > 0$.    Тогда    коэффициенты    $b$   и   $a$    имеют разные знаки.
• Ось параболы левее     $у$   -   ординаты     $\Leftrightarrow$      $-\frac{b}{2a} < 0$.    Тогда    $b$   и   $a$    имеют одинаковые знаки.   А когда    $b=0$ ?

Теорема.     Графиком   функции      $y=ax^2+bx+c$     является    парабола,   которая   получается   из    $y=ax^2$   параллельным переносом.                   

• Построить график функции     $y=ax^2+bx+c$     можно параллельным переносом параболы     $y=ax^2$.
• Обе ветви    параболы      $y=ax^2+bx+c$    направлены   вверх,   если    $a > 0$ . Ветви направлены вниз,   если   $a < 0$.
  
• Ось   параболы - вертикальная линия - имеет уравнение    $x=-\frac{b}{2a}$ .    Ось   - делает "зеркальную   симметрию".
  
• Координаты   вершины параболы    $\left(-\frac{b}{2a};\frac{4ac-b^2}{4a}\right)$.   Вершина находится на оси параболы.
  
• Пересечения параболы   с   осью   $X$ - абсцисс   дают   корни   квадратичной   функции. Там значение функции = 0.
• Пересечение   с   осью   $Y$ - ординат   происходит   в точке   при   $x=0$. Т.е.   $y=0+0+c$.   Точка $(0;c)$

         

Наименьшее и наибольшее значения на заданном отрезке   

Посмотри выше гифку о нахождении наибольших и наименьших значений параболы,   как анализируются график,   значения,   поведение функции.

Алгоритм    построения   параболы      $y=ax^2+bx+c$ :    

• Найти    координаты   вершины параболы,   отметить ее точку на координатной   плоскости, провести   ось   параболы,
• отметить   на   оси   $OX$   две точки, симметричные относительно   оси   параболы,   найти   значения   функции в в   этих   точках;
• построить   на   координатной   плоскости   соответствующие   точки: вершину параболы, еще две точки, симметричные от оси параболы.
  
• через   полученные    три   точки       плавно провести   параболу, ветви продолжить "до бесконечности".
  
• или:    взять   еще   пару//   точек,   симметричных $\pm3$ относительно   оси   параболы,   и построить   параболу   по   5-ти   точкам**.

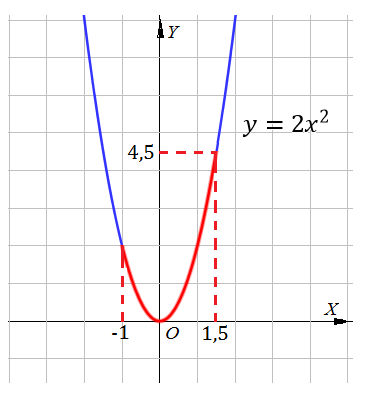
Пример 3:          Найти наименьшее и наибольшее значения функции   $y=2x^2$    на отрезке : а) $\left[0;2\right]$,   б) $\left[-2;-1\right]$,   в) $\left[-1;1,5\right]$ .

• а) см. рис $(1)$ -   график   функции     $y=2x^2$;      выделена его   часть   на   отрезке   $\left[0;2\right]$.    Визуально видно, что:
  
• наименьшее значение     $m=0$     функция   достигает   в   точке     $x=0$,     а   наибольшее   значение     $M=8$      при     $x=2$.
• б) выделим   на   графике    $y=2x^2$,    часть   на   отрезке    $\left[-2;-1\right]$.   Видно,   что ...
• наименьшее   значение    $m=2$ функция   достигает   в   точке     $x=-1$,    а наибольшее    $M=8$    при   $x=-2$.
• в) рассмотрим график на отрезке    $\left[-1;1,5\right]$.    Наименьшее   значение     $m=0$   в   т.   $x=-1$;    Наибольшее    $M=4,5$ в     $x=1,5$.

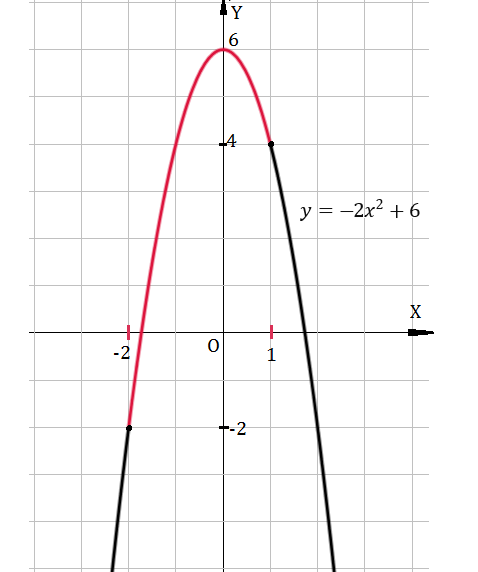
Пример 4:          Найти наименьшее и наибольшее значения функции   $y=-2x^2+6$    на отрезке   $\left[-2;1\right]$.

• Построим   график   функции    $y=-2x^2+6$   и выделим   его   часть    на   отрезке    $\left[-2;1\right]$.    Смотри   $(2)$- ой   рис.
• Видно:     наименьшее    $m=-2$     достигается   при    $x=-2$,      наибольшее    $M=6$   достигается   при   $x=0$.
  
• Ответ:           $y_{min}=-2$,      $y_{max}=6$ .    
  

(1)        (2)          (3)            (4)       

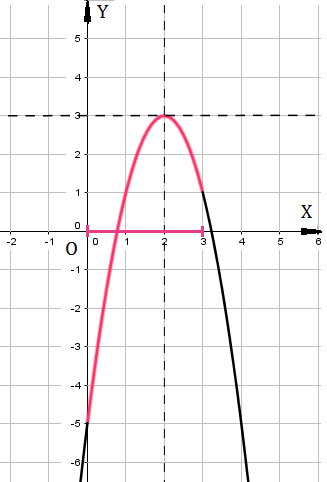
Пример 5:          Найти наименьшее и наибольшее значения функции    $y=-2x^2+8x-5$    на отрезке   $\left[0;3\right]$.

• воспользуемся   алгоритмом   и   построим   параболу      $y=-2x^2+8x-5$ .     Смотри   $(3)$-й   рисунок.   Найдем вершину.
  
• координаты вершины    параболы     $x=-\frac{b}{2a}$;        $y=\frac{4ac-b^2}{4a}$        :        $x=-\frac{8}{2\cdot\left(-2\right)}=\frac{8}{4}=2$;        $y=\frac{4\cdot\left(-2\right)\cdot\left(-5\right)-8^2}{4\cdot\left(-2\right)}=\frac{40-64}{-8}=3$.
• вершиной параболы - точка    $\left(2;3\right)$.     Осью параболы является вертикальная прямая      $x=2$.     
  
• возьмем на оси   $OX$   две точки, симметричные    $\pm2$      относительно оси параболы      $x=2-2=0$      и      $x=2+24$.
• Вычислим функцию в этих точках:     $f\left(0\right)=f\left(4\right)=0+0-5=-5$.   
  
• Отметим   точки     $\left(0;-5\right)$   и    $\left(4;-5\right)$   на координатной плоскости.   Через   полученные   три   точки проведем параболу.
  
• Видно по    отрезку   $\left[0;3\right]$:      наименьшее    $m=-5$     достигается   при    $x=0$,    наибольшее    $M=3$    достигается   при    $x=2$.

Графическое решение уравнений   

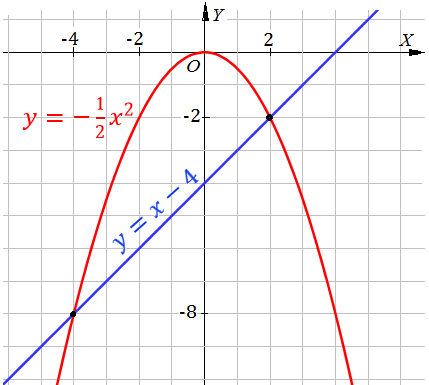
Пример 6:          Решите уравнение              $-\frac{1}{2}x^2=x-4$                  графическим способом.

• Построим параболу     $y=-\frac{1}{2}x^2$     и     прямую      $y=x-4$.   Решения уравнения находим по точкам   пересечения    графиков.
• Смотри   $(4)$- ой   рис: В каких точках пересекаются парабола и прямая? Какие координаты у этих точек? Что там выравнивается?
• $\left(-4;-8\right)$   и   $\left(2;-2\right)$ .   Абциссы   этих   точек   и   являются корнями    данного   уравнения. Почему?
  
• потому, что именно   для этих   $x$ :     значения графиков,   а   значит   и   функций,   значит   левой   и   правой   частей   выравниваются.
• Ответ:      $x=-4$,     $x=2$.

Пример 7:          Решите систему уравнений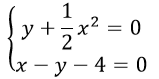         

• Преобразуем   первое   уравнение   системы   к виду     $y=-\frac{1}{2}x^2$ ,     второе   уравнение системы   к   виду     $y=x-4$ .
  
• по   чертежу   на   $4$-м   рисунке   найдем:    две   точки   пересечения    графиков:      $\left(-4;-8\right)$   и   $\left(2;-2\right)$ .
  
• Координаты   этих точек   и   являются решениями    заданной   системы.       Ответ:         $\left(-4;-8\right)$ ,     $\left(2;-2\right)$.

Пример 8:          Дана функция    $y=f\left(x\right)$,    где     $f\left(x\right)=3x^2+x-1$ .    Найти : $f\left(-x\right)$,    $f\left(2x\right)$,   $f\left(x^2\right)$, $f\left(x^3\right)$ ,   $f\left(x^2-2x\right)$.

• $f\left(-x\right)=3\left(-x\right)^2+\left(-x\right)-1=3x^2-x-1$
• $f\left(2x\right)=3\left(2x\right)^2+\left(2x\right)-1=12x^2+2x-1$                   
  
• $f\left(x^2\right)=3\left(x^2\right)^2+x^2-1=3x^4+x^2-1$                             
  
• $f\left(x^3\right)=3\left(x^3\right)^2+x^3-1=3x^6+x^3-1$
• $f\left(x^2-2x\right)=3\left(x^2-2x\right)^2+\left(x^2-2x\right)-1=3\left(x^4-4x^3+4x^2\right)+x^2-2x-1=13x^4-12x^3+13x^2-2x-1$

Дан график (парабола)   ...    найти функцию (коэффициенты)   

Пример 9:    На рисунке изображён график функции       $y=ax^2+bx+c$ .        Найдите    $f(2)$.

Пример 10:      На рисунке изображены графики функций видов   $f(x)=ax^2+bx+c$    и   $g(x)=kx$ пересекающиеся в точках   $A$   и   $B$.    Найдите абсциссу точки   $B$.

• Коэффициенты   квадратной $f(x)$   и линейной $g(x)$ функций находим через точки их графиков, составляя равенства.
• Пересечение графиков f(x) и g(x)    определяется корнями уравнения f(x) = g(x).       Выравнивание!!!
• Точка А и так видна. Точка В имеет такую х - координату,   в котором выполняется уравнение       $ax^2+bx+c=kx$.

Упражнения (А):

Упражнения (В):

Упражнения (C):