Графический способ решения уравнений

Как решать уравнения с помощью графиков?

Визуальное решение уравнения:    построим график левой части уравнения. Он покажет, какие значения принимает левая часть при разных значениях неизвестного. Построим фото правой части, его график покажет какие значения принимает в разных точках. Для поиска корня уравнения нам нужно "поймать" ту точку, в которой левая и правая части выравниваются. Значит, надо искать пересечение этих графиков: для такого х - неизвестного обе части уравнения будут равны. Итак: точки пересечения этих графиков дадут нам корни уравнения - х - координата этих точек удовлетворяет уравнению.

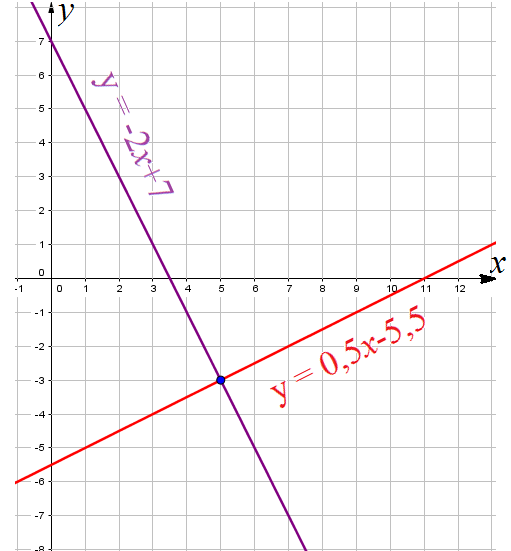
Пример 1:                  Решить уравнение              $-2x+7=0,5x-5,5$                графическим способом.

• Построим   прямые      $y=-2x+7$        и        $y=0,5x-5,5$.     По   чертежу   найдем   точку   пересечения    графиков
  
• $\left(5;-3\right)$.        абсцисса   этой   точки   является   корнем   данного   уравнения,
  
• потому   что,   именно   для   этого    $x$   значения
• графиков,   а   значит   и   функций,   значения   левой   и   правой   частей выравниваются.              ответ:    $x=5$.

                               

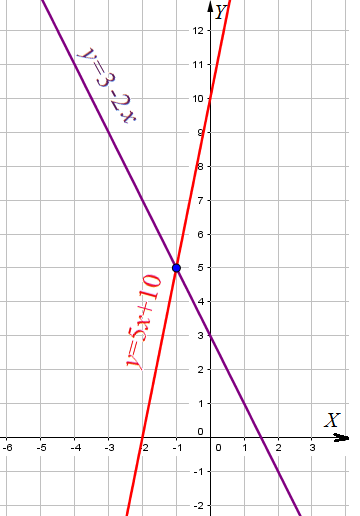
Пример 2:             Решить систему уравнений              {   $2x+y=3$;   $y-5x=10$   }

• Преобразуем   первое   уравнение   системы   к виду     $y=3-2x$,      второе уравнение системы к   виду     $y=5x+10$
• по   чертежу найдем точку пересечения графиков:   $\left(-1;5\right)$.    Координаты   этой точки и являются   решением   системы.
• При таких      $x$    и   $y$    оба    уравнения   системы выравниваются,   значит   такое   решение   удовлетворяет   уравнение.
• ответ:        $x=-1$ ;         $y=5$

Графический способ решения уравнений с радикалами

Пример 3:     Решите графически уравнение . $\sqrt{x}=6-x$

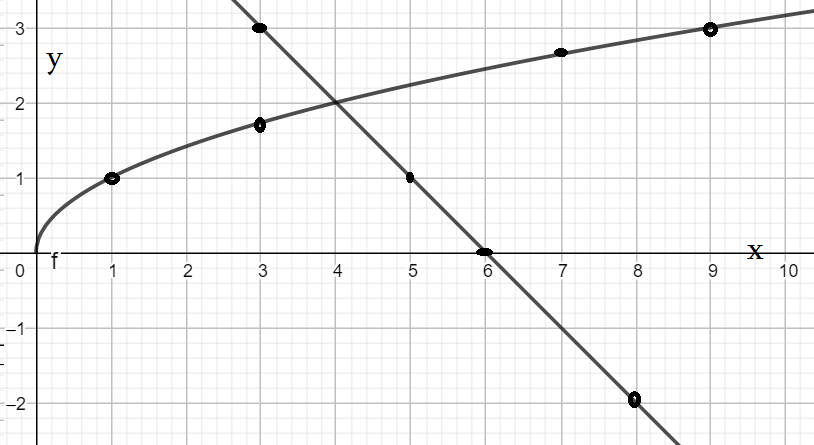
• Построим графики функций $y=\sqrt{x}$    и   $y=6-x$ в одной координатной плоскости.
• Вычислим значения функции из левой части уравнения: $f\left(x\right)=\sqrt{x}$   в нескольких точках:   
  
• $f\left(1\right)=1$         $f\left(3\right)\approx1,7$      $f\left(7\right)\approx2,7$          $f\left(9\right)=3$    $f\left(12\right)\approx3,5$.
• Составим список точек:       $(1;1)$        $(3;1,7)$    $(7;2,7)$    $(9;3)$    $(12;3,5)$ .    По точкам проведем график.
  
• Составим список точек для функции $y=6-x$:   $(0;6)$        $(1;5)$    $(3;3)$    $(6;0)$    $(8;-2)$ . Проведем график - линию.
• Где, в какой точке эти графики пересекаются?   Визуально видно, что в точке     $(4;2)$. Что это значит?
• При аргументе    $x=4$   обе функции принимают одно и тоже значение. Значит, равны     $\sqrt{x}=6-x$.   Ответ: $x=4$
• Вывод:    Для нахождения решения уравнения надо "увидеть" точку пересечения графиков левой и правой частей.

                             

Пример 4:     Решите графически уравнение . $\sqrt{x-1}=3-x$   

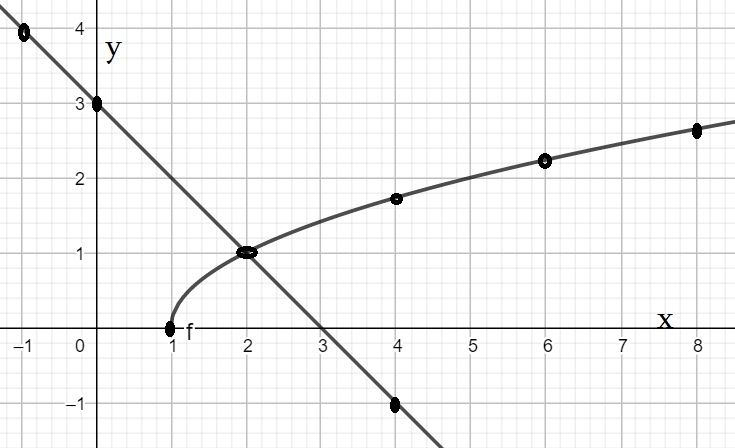
• Решением уравнения будет то число $x$, при котором пересекаются графики функций     $y=\sqrt{x-1}$    и    $y=3-x$
  
• Точки графика функции $y=\sqrt{x-1}$:            $(1;0)$        $(4;1,7)$        $(6;2,3)$        $(8;2,7)$       $(10;3)$ .
  
• Точки графика линейной функции $y=3-x$:            $(-1;4)$        $(0;3)$        $(4;-1)$        $(7;-4)$       $(10;-7)$ .
  
• Видно, что графики пересекаются в точке с координатами $(2;1)$ . Значит, при $x=2$ обе функции имеют значение $1$.
• Это означает, что и левая и правая части в этой точке равны ... т.е. это решение уравнения      Ответ: $x=2$.

Графический способ решения дробно - рациональных уравнений

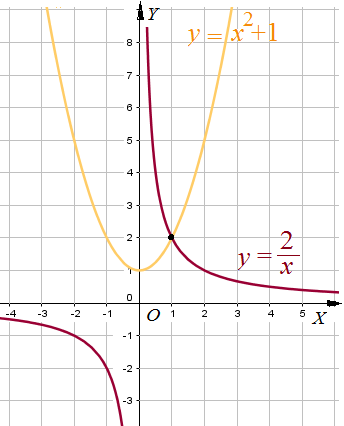
Пример 5:                Решить уравнение         $\frac{2}{x}=x^2+1$       графическим   способом.

• Рассмотрим   две   функции :      $y=\frac{2}{x}$      и      $y=x^2+1$      построим   гиперболу      $y=\frac{2}{x}$      и   параболу      $y=x^2+1$      по
• чертежу   видно,   что   графики   пересекаются   в   точке   с   координатами    $\left(1;2\right)$.   если   подставить   $x=1$    в   уравнение,
• то   равенство   выполняется:      $\frac{2}{1}=1^2+1$     обе   функции   принимают   одно   и   то   же   значение      $2=2$.    
  
• ответ:      $x=1$.      при   таком    $x$    графики   пересекаются.
• "почему?":   при   каких    $x$ - числах   выравниваются   обе   части   уравнения?   при   тех    $x$ - числах,   при   которых   левая
• функция   и   правая   функция   приобретают   одинаковые   значения    ...    это   то   же   самое,   что   графики   этих   функций
• пересекаются   в   точках с   такими   $x$   -   координатами.
  

                                                         

Пример 6:                Решить уравнение                            $\frac{5}{x}=x-4$.

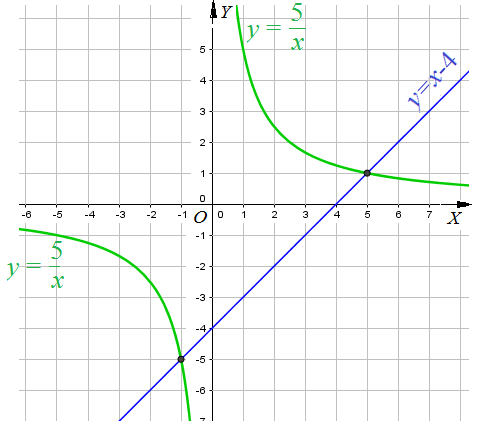
• рассмотрим две функции:     $y=\frac{5}{x}$     и      $y=x-4$,     построим   их   графики:   гиперболу    $y=\frac{5}{x}$    и   прямую   $y=x-4$.
• по   чертежу   видно,   что   гипербола   и   прямая   пересекаются   в   точках   $(-1;-5)$    и    $(5;1)$.    проверим,   подставим
• $x=-1$     и       $x=5$    в   уравнение :      $\frac{5}{-1}=-1-4$       $\Leftrightarrow$        $-5=-5$       и              $\frac{5}{5}=5-4$     $\Leftrightarrow$     $1=1$ .      равенство
• выполняется,   значит   данное   уравнение   имеет   два   корня   -   абсциссы   точек   пересечения   графиков.
  
• ответ:       $x_1=-1$;      $x_2=5$.

Упражнения: