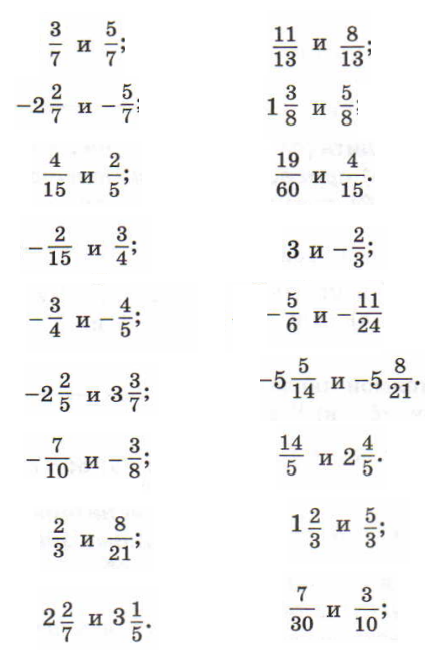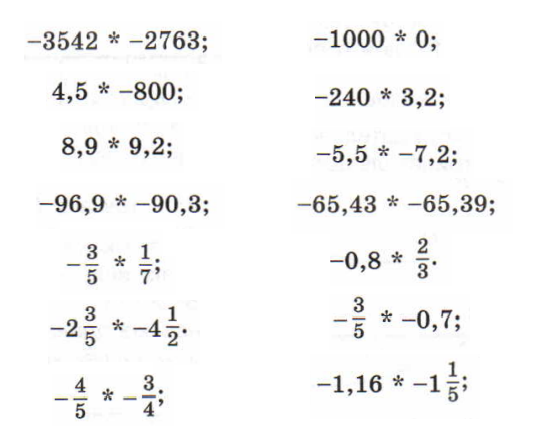Свойства числовых неравенств:

Свойство 1: если $a > b$ и $b > c$ $\Rightarrow$ $a > c$ свойство транзитивности;
Свойство 2: если $a > b$ $\Rightarrow$ $a+c > b+c$ добавление слагаемого к обеим частям не меняет знак неравенства;
это свойство позволяет выполнить операцию "перенос слагаемого".
Свойство 3: если $a > b$ и $m > 0$ $\Rightarrow$ $am > bm$,
после умножения обеих частей неравенства на положительное число, знак неравенства не меняется.
если $a > b$ и $m < 0$ $\Rightarrow$ $am < bm$ ,
после умножения обеих частей неравенства на отрицательное число, знак неравенства меняется.
Свойство 4: если $a > b$ и $c > d$ $\Rightarrow$ $a+c > b+d$ одноименные неравенства можно почленно складывать.
Свойство 5: если $a$, $b$, $c$, $d$ - положительные числа и $a > b$, $c > d$, $\Rightarrow$ $a\cdot c > b\cdot d$
одноименные неравенства можно почленно умножать.
Свойство 6: если $a$ и $b$ - неотрицательные числа и $a > b$ $\Rightarrow$ $a^n > b^n$, где $n$ - любое натуральное число
при возведении в натуральную степень знак неравенства не меняется.

Сравнение чисел:
Сравнение чисел: Из двух чисел меньше то, которому на координатной оси соответствует точка левее, а больше то, которому на координатной оси соответствует точка, расположенная правее.
Свойства сравнений: любое отрицательное число меньше нуля. любое положительное число больше нуля. Любое отрицательное число меньше любого положительного числа.
Изображение числа : Каждое число изображается в виде точки на оси координат. Числа на числовой оси выглядят точками. У каждого числа своя точка. У каждой точки свое число. Для того чтобы построить точку, соответствующую некоторому числу $a$ , нужно: 1) определить знак этого числа ; 2) от начала координат отложить отрезок , равный $∣a∣$ вправо , если знак "+" и влево , если знак "-" . Число $a$ в таком случае называют координатой построенной точки . Числа - это «адреса» точек на числовой прямой. Точки - это "фотографии" чисел.
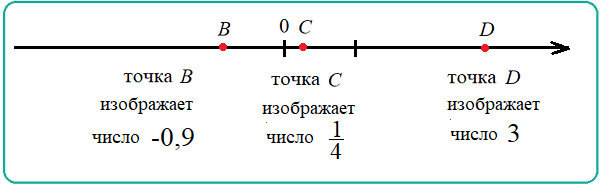
Пример 1: На рисунке числа $3$, $\frac{1}{4}$ , $−0,9$ изображены точками $B$, $C$ , $D$ . При этом только $B$ левее нуля, а точка $D$ самая правая. Какая буква какому числу соответствует?
- Если $B$ левее нуля, то число какого знака она изображает? А точки справа от 0 какими знаками представлены.
- $D$ самая правая - значит ли это, что ее число должно быть самым большим?... Чем правее, тем больше?
Пример 2: Сравнить десятичные числа
- $15,34$ и $12,1$ ? Целая часть 1-го $15$ больше, чем у 2-го, $12$. Значит, $15,34>12,1$
- $-15,34$ и $-12,1$ ? $15$ больше $12$ . 1-ое на числовой оси левее, чем 2-ое: $-15,34<-12,1$
- $15,34$ и $-12,1$ ? Положительное число правее $0$, отрицательное левее $0$. Значит, всяко 1-ое правее 2-го: $15,34>-12,1$
- $7,65337819$ и $7,65327819$ ? Смотрим и сравниваем цифры слева направо. В какой цифре различие? $7,65337819>7,65327819$
Пример 3: Сравнить дробные числа
- $\frac{5}{13}$ и $ \frac{6}{13}$ ? При одинаковых знаменателях: надо сравнить числители .... $\frac{5}{13}<\frac{6}{13}$
- $\frac{7}{10}$ и $\frac{8}{15}$ ? При разных знаменателях "подведем" к общему $30$: $\frac{21}{30}>\frac{16}{30}$ и сравним: $\frac{7}{10}>\frac{8}{15}$
- $\frac{7}{10}$ и $-\frac{8}{15}$ ? Отрицательно всяко меньше положительного. Левее ..... $\frac{7}{10}>-\frac{8}{15}$
- $0,51$ и $\frac{8}{15}$ ? Приближенно, через деление $\frac{8}{15}\approx0,53$ . Очевидный вывод: $0,51<\frac{8}{15}$
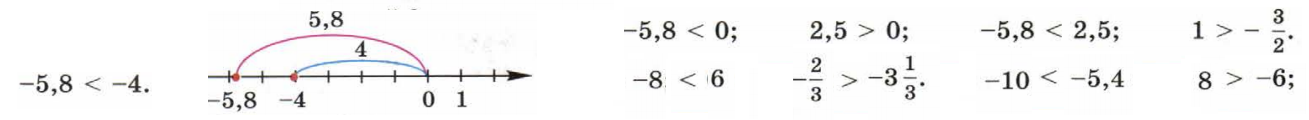
Пример 4: Расположить числа в порядке возрастания $\left(-3\right)^2$, $-(-2)^3=8$, $10\cdot\left(-1,11\right)^2$, $-3^2$ , $3\cdot2^2$
- Вычислим аккуратно каждое число, чтоб понять их "размер": $\left(-3\right)^2=9$ $-3^2=-9$
- $-(-2)^3=8$ $3\cdot2^2=12$ $10\cdot\left(-1,11\right)^2=12,321$
- Ясен порядок возрастания: $-3^2<-(-2)^3<\left(-3\right)^2<3\cdot2^2<10\cdot\left(-1,11\right)^2$
Замечание : Есть ученики, которые думают что $-5^2=25$ . "Что слышу, то и вижу". Но здесь вижу, что в квадрате $5$ , а не $-5$ . Если Вы хотите, чтоб $-a$ в квадрат возводился , то надо писать основание в скобке $\left(-a\right)^2$. Так что $-5^2=-25$, $(-5)^2=+25$ . Хороший вопрос для проверки синтаксиса: что под квадратом?
Пример 5: Сравнить числовые выражения $0,1\cdot0,77\cdot0,121$ и $2,5\cdot \frac{5,6\cdot 10^{-7}}{2,1\cdot 10^{-5}}$
- Стратегия "как сравнить два числовых выражений": предположим, что первое меньше второго ,
- затем по свойствам числовых неравенств преобразуем нашу гипотезу до "очевидного".
- Если придем к верному неравенству, значит наше предположение оправдалось , ....
- .... в противном случае, исходное неравенство выполняется "ровно наоборот".
- "Сравнить числа" = составить с ними неравенство, которое нужно доказать или опровергнуть.
- "рабочая гипотеза": $0,1\cdot0.77\cdot0.121 < 2,5\cdot\frac{5,6\cdot10^{-7}}{2,1\cdot10^{-5}}$
- эквивалентные преобразования числового неравенства : $\frac{7}{100000}\cdot11\cdot121 < 5\cdot\frac{8}{3}\cdot\frac{1}{100}$ $\Leftrightarrow$
- $\frac{7}{100000}\cdot11\cdot121 < \frac{20}{3}\cdot\frac{1}{100}$ $\Leftrightarrow$ $7\cdot1331\cdot3 < 2\cdot10000$ $\Leftrightarrow$ $27951 < 20000$ , что "очевидно неверно" ,
- значит $\Rightarrow$ $0,7\cdot0.77\cdot0.777 > 2,5\cdot\frac{5,6\cdot10^{-7}}{2,1\cdot10^{-5}}$
Пример 6: Расположить по убыванию числа $a-1$ ; $2+a$ ; $-a^2$ ; $-\frac{1}{a}$ , если число $a$ из интервала $-3 < a < -2$.
- Возьмем из интервала приближенное $a\approx-2,4$ . посмотрим, чему будет равно каждое из выражений:
- $a-1\approx-2,4-1\approx-3,4$ ; $2+a\approx-0,4$ ; $-a^2\approx-5,76$ ; $-\frac{1}{a}\approx0,41$
- сравним получившиеся значения и выстроим убывающую последовательность.
- Ответ : $-\frac{1}{a}>2+a>a-1>-a^2$
Интерактивная Доска:
Упражнения: