Сократить дробь - значит разделить числитель и знаменатель этой дроби на одно и то же число.
- сократить $\frac{16}{20}$ на $4$ значит разделить и числитель $16$, и знаменатель $20$ на число $4$.
- после деления мы получим равную $\frac{16}{20}$ - м дробь. $\frac{16}{20}=\frac{16:4}{20:4}=\frac{4}{5}$
Сокращение дробей - это способ упрощения выражения, содержащего дробь.
-
$\frac{16}{20}=\frac{4}{5}$ разделили числитель и знаменатель на $4$. дробь стала состоять из меньших чисел. выглядеть попроще.
-
$\frac{150}{250}=\frac{15}{25}=\frac{3}{5}$ здесь от дроби с трёхзначными числами перешли к дроби с однозначными числителем и знаменателем.
До какого момента можно сокращать дробь? Пока в числителе и в знаменателе не останутся взаимно простые числа.
Пример 1: Сократить $\frac{210}{840}=\frac{21}{84}=\frac{7}{28}=\frac{1}{4}$
-
- выделим множитель $10$ в числителе и в знаменателе.
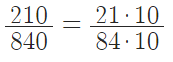
- выделим множитель $10$ в числителе и в знаменателе.
-
- разделим обоих на этот множитель(делитель).
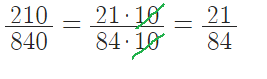 получили равную дробь, но попроще.
получили равную дробь, но попроще.
- разделим обоих на этот множитель(делитель).
-
- выделим ещё общие делители
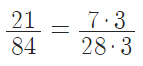
- выделим ещё общие делители
-
- сократим(разделим) на $3$.
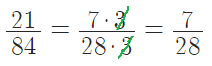 получили дробь ещё проще.
получили дробь ещё проще.
- сократим(разделим) на $3$.
-
- заметим, что и числитель, и знаменатель делятся на $7$.
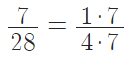
- заметим, что и числитель, и знаменатель делятся на $7$.
-
- сократим на последний общий делитель числителя и знаменателя.
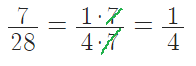
- сократим на последний общий делитель числителя и знаменателя.
-
- от $\frac{210}{840}$ пришли к $\frac{1}{4}$. $\frac{1}{4}$ уже сокращать нельзя. потому что $1$ и $4$ не имеют общих делителей.
иначе говоря, $1$ и $4$ взаимно простые числа.
- от $\frac{210}{840}$ пришли к $\frac{1}{4}$. $\frac{1}{4}$ уже сокращать нельзя. потому что $1$ и $4$ не имеют общих делителей.
Основное свойство дроби: Если числитель и знаменатель алгебраической дроби поделить на одно и то же ненулевое выражение, то получится алгебраическая дробь, равная прежнему: дробь не изменится.
$\frac{A\cdot X}{X\cdot B}=\frac{A\cdot X:X}{X\cdot B:X}=\frac{A\cdot1}{1\cdot B}=\frac{A}{B}$ $X\ne0$ $B\ne0$
Сократить дробь - значит разделить числитель и знаменатель этой дроби на один и тот же множитель.
Алгоритм сокращения алгебраических дробей
- Разложить числитель и знаменатель дроби на множители.
- Найти общие множители.
- Разделить числитель и знаменатель на общие множители.
Пример 2: Сократить дроби $\frac{7a}{ax}$ $\frac{6m}{-9m}$ $\frac{10ab^6c}{15a^3b^2x}$ $\frac{8\left(a-b\right)}{a-b}$
$\frac{7a}{ax}=\frac{7\cdot a}{a\cdot x}=\frac{7\cdot [a]}{[a]\cdot x}=\frac{7\cdot [1]}{[1]\cdot x}=\frac{7}{x}$ общий множитель $a$
$\frac{6m}{-9m}=\frac{6\cdot [m]}{-9\cdot [m]}=\frac{2\cdot3\cdot [1]}{-3\cdot3\cdot [1]}=-\frac{2}{3}$ общий множитель $3m$
$\frac{10ab^6c}{15a^3b^2x}=\frac{10ab^6c:[5ab^2]}{15a^3b^2x:[5ab^2]}=\frac{2b^4c}{3a^2x}$ общий множитель $5ab^2$
$\frac{8\left(a-b\right)}{a-b}=\frac{8\left(a-b\right):[a-b]}{(a-b):[a-b]}=8$ общий множитель $a-b$
Упражнения
