Координатная плоскость: Два числа - Одна точка плоскости.




Так же как простую прямую можно превратить в координатную, так и обычную плоскость можно превратить в координатную . Для этого на плоскости нужно провести две перпендикулярные координатные прямые с одинаковыми единичными отрезками $x$ и $y$ , которые пересекаются в начале отсчёта — точке $0$ . Так будет задана прямоугольная система координат или декартова.
прямоугольная система координат положение точки определяется двумя её координатами - абциссой и ординатой .
- На прямой положение точки определяется одной координатой, а на плоскости в системе координат положение точки определяется двумя её координатами - абциссой и ординатой .
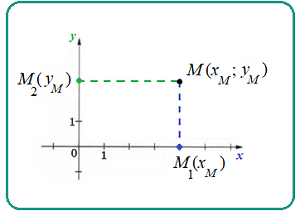
- Любой точке $M$ координатной плоскости сопоставляются $(x_M;y_M)$ - два числа, пара чисел, две его координаты:
- Для получения этих координат необходимо через точку $M$ провести две прямые, параллельные координатным осям.
- Одна прямая пересечёт ось абсцисс (ось $X$) в точке с абсциссой $x_M$ - первое число в паре координат ,
- вторая прямая пересечёт ось ординат (ось $Y$) в точке с ординатой $y_M$ - второе число в паре координат.
- Четыре прямых угла, образованных координатными осями, называются координатными углами: $I$ , $II$ , $III$ и $IV$ четверти.

Пример 1: Построить точки по заданным координатам $А(2;5)$, $В(3;1)$ . Отметить точки $M(3;-1)$, $N(-5;-2)$
- Для построения точки по ее координатам нужно:
- отсчитать по $x$ - горизонтали количество единиц, заданной первым числом. Если положительно, то вправо от 0. Иначе, влево.
- Затем: отсчитать по $y$ - вертикали столько, сколько указано вторым числом в координатах. Если отрицательно, то вниз от 0. Иначе вверх.





Пример 2: Определить координаты точек $А$, $В$ , $C$.
- Посмотреть на точку: сколько единиц по $x$ - горизонтали, правее или левее от 0, сколько по $y$ - вертикали, вверх или вниз?
- Знаки? по тому как вправо-влево по $x$, вверх- вниз по $y$. Ответ: $А(1;3)$, $В(-3;5)$ , $C(4;2)$.




Координатные углы . Четверти координатной плоскости $I$, $II$, $III$, $IV$.
- Если точка имеет положительную абсциссу $x>0$ и положительную ординату $y>0$ , то она лежит в $I$ четверти.
- Если точка имеет отрицательную абсциссу $x<0$ и положительную ординату $y>0$ , то она лежит во $II$ четверти.
- Если точка имеет отрицательную абсциссу $x<0$ и отрицательную ординату $y<0$ , то она лежит в $III$ четверти.
- Если точка имеет положительную абсциссу $x>0$ и отрицательную ординату $y<0$ , то она лежит в $IV$ четверти.



Пример 3: Построить точки по заданным координатам $M(1;3)$ , $N(3;1)$ .
- a) для построения точки $M$ необходимо отложить единицу на оси $x$ и провести перпендикулярную прямую, (Рис. 1).
- на оси $Y$ откладываем число $3$ и проводим перпендикулярную оси $y$ прямую ...на пересечении перпендикуляров получим точку $M$ с координатами $(1;3)$.
- б) для построения точки $N$ необходимо отложить на оси $x$ число $3$ и провести перпендикулярную оси $x$ прямую;
- на оси $y$ откладываем число $1$ и проводим перпендикулярную оси $y$ прямую $\Rightarrow $ на пересечении перпендикуляров получим точку $N$ с координатами $(3;1)$ .
(1)  (2)
(2)  (3)
(3)  (4)
(4) 
Пример 4: Определить в каком координатном углу находится точка по заданным знакам координат.
- а) Где находится $M\left(x_M;y_M\right)$ , если $x_M<0$ и $y_M>0$ ?
- построим координатную плоскость и обозначим на ней точку $M$ (Рис. 2). Ответ: точка $M$ лежит в $ΙΙ$ четверти.
- б) Где находится $N\left(x_N;y_N\right)$ , если $x_N<0$ и $y_N<0$ ?
- построим координатную плоскость и обозначим на ней точку $N$ (рис.3) . Ответ: точка $N$ лежит в $ΙΙΙ$ четверти.
- в) Где находится $P\left(x_P;y_P\right)$ , если $x_P<0$ и $y_P>0$ ?
- построим координатную плоскость и обозначим на ней точку $P$ (рис. 4).Ответ: точка $P$ лежит в $ΙV$ четверти.
Пример 5: Определить в каких координатных углах может находиться точка, если известен знак только одной из координат.
- а) Где находится точка , если у нее положительная ордината $(x;y>0)$ ?
- т.к ордината точки больше нуля $y>0$, а знак абсциссы не задан $\Rightarrow $ точка может лежать и в первом (т. $M$) и во втором (т. $N$ ) координатном углу (Рис. 5). Ответ: $Ι$ , $ΙΙ$.
- б) Где находится точка , если у нее отрицательная ордината $(x;y<0)$ ?
- рассуждаем: так как ордината точки меньше нуля $y<0$, а знак абсциссы не задан $\Rightarrow $ точка лежит в третьем (т. $M$) или в четвертом (т. $N$ ) координатном углу (Рис. 6). а) Ответ: $ΙΙΙ$ , $ΙV$.
- в) Где находится точка , если у нее положительная абцисса $(x>0;y)$ ?
- абцисса точки больше нуля $x>0$, знак ординаты может быть любой $\Rightarrow $ точка может принадлежать и первому (т. $M$) и второму (т. $N$ ) координатному углу (Рис. 7). а) Ответ: $Ι$ , $ΙV$.
- г) Где находится точка , если у нее отрицательная абцисса $(x<0;y)$ ?
- абцисса точки меньше нуля $x<0$, а знак ординаты не задан $\Rightarrow $ точка принадлежит второму (т. $M$) или третьему (т. $N$ ) координатному углу (Рис. 8). а) Ответ: $ΙΙ$ , $ΙΙΙ$.
(5)  (6)
(6)  (7)
(7) (8)
(8)
Пример 6: Построить точки $M(4;1)$ , $N(4;0)$ , $P(4;-3)$ , $K(4;3)$ и где они лежат?
- построим координатную плоскость и обозначим на ней заданные точки. у точек абсцисса одинаковая и равна $4$,
- следовательно, все они лежат на одной вертикальной прямой (Рис. 9), уравнение которой $x=4$.
- Ответ: все заданные точки лежат на прямой $x=4$.
Пример 7: Построить точки $M(1;3)$ , $N(-3;3)$ , $P(5;3)$ и определить на какой прямой они лежат.
- построим координатную плоскость и обозначим на ней заданные точки. у точек одинаковая ордината равная $3$
- все точки лежат на одной горизонтальной прямой (Рис. 10), уравнение которой $y=3$.
- Ответ: все заданные точки лежат на прямой $y=3$.
(9) (10)
(10)  (11)
(11) 
Пример 8: Составить уравнения прямых и написать координаты точек их пересечения по данным рисунка (11) .
- по рисунку видно , что абсцисса точки $M$ равна $5$ , а ордината равна $4$
- прямые $KM$ и $MN$ пересекаются в точке $M(5;4)$.
- аналогично находим координаты других точек: $N(5;-3)$ , $P(-3;3)$ , $K(-3;4)$ .
- уравнение вертикальной прямой $MK$ $y=4$ : ордината у любых точек этой прямой равна $4$ .
- уравнение вертикальной прямой $NP$ $y=-3$ , так как ордината каждой точки этой прямой равна $-3$.
- уравнение горизонтальной прямой $MN$ $x=5$ , так как абсцисса у всех точек этой прямой равна $5$.
- $KP$ - горизонтальная прямая и абсцисса каждой её точки равна $-3$ $\Rightarrow $ уравнение $KP$ $x=-3$ .
- Ответ: $(MK)$ $y=4$; $(NP)$ $y=-3$; $(MN)$ $x=5$ ; $(KP)$ $x=-3$ ; $M(5;4)$ , $N(5;-3)$ , $P(-3;3)$ , $K(-3;4)$ .
Упражнения:
Ответьте на вопросы:
- Как построить точку $A(-2;5)$?
- Какие знаки имеют координаты точек во втором координатном углу?
- В какой четверти располагается точка $B(4;2)$ ?
- Постройте фигуру по заданным точкам: $(-2;2)$ , $(2;2)$ , $(2;-2)$ , $(0;0)$ , $(-2;-2)$ , $(-2;2)$ .
- Отметьте на координатной плоскости точки $M(-6;3)$ , $N(3;0)$ , $K(-2;1)$ , $P(1;-2)$ . Проведите прямые $MN$ и $КР$ и найдите координаты их точки пересечения .

Иллюстрация координатной оси:







https://interneturok.ru/algebra/7-klass/glava-2-lineynaya-funktsiya/koordinatnaya-ploskost
Координатная ось - "фотография" чисел в виде точек на прямой ##
пробa Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось.

Чтобы из любой прямой получить координатную ось , необходимо выбрать на ней нулевую точку $0$ - это будет началом отсчета ; отметить точку $1$ - определить единичный отрезок (т.е. выбрать масштаб) и нарисовать стрелочку в положительном направлении отсчёта . На координатной оси изображается взаимооднозначные соответствия между точками и числами . Например, числу $3$ на координатной прямой сопоставляется единственная точка $A$ ,
точке $B$ - единственное число $-2$ , такое число назвали координатой.
Координатная прямая — это прямая с указанными на ней началом отсчёта O (0) , направлением и единичным отрезком.
пробa Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. Мы будем изучать координатную плоскость с прямоугольной системой координат.
Координаты точек на прямой.
пробa Точка $O$ разбивает прямую $AB$ на два луча $OA$ и $OB$ . Если примем точку $O$ за начало отсчета , выберем на ней единичный отрезок и положительное направление , то мы превратим эту прямую в координатную ось . Рассмотрим на ней произвольную точку . Как определить ее положение? Для ответа на этот вопрос придумали понятие - координата . Положение любой точки на координатной оси задается её координатой. Чтобы отличить друг от друга координаты , перед числами на левом луче $OA$ условились ставить знак «минус » , а перед числами на правом луче $OB$ - знак «плюс».

Координаты со знаком "$-$" называются отрицательными . Координаты со знаком «+» называются положительными .
Точка $O$ - начало отсчета или начало координат , изображает ноль. Само число $0$ не является ни положительным ни отрицательным , только отделяет положительные и отрицательные числа друг от друга .
Координата точки - это число , показывающее положение точки на прямой.
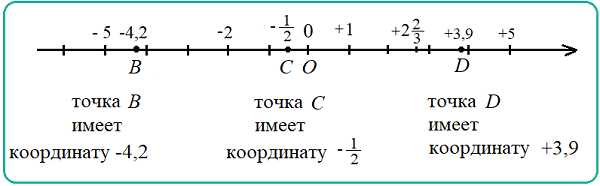
Записывают координаты точек $B$ , $C$ , $D$ следующим образом: $B(-4,2)$ , $C\left(-\frac{1}{2}\right)$ , $D(3,9)$ .
Изображение чисел точками на координатной оси.
Числа на координатной прямой выглядят точками. Для того чтобы построить точку, соответствующую некоторому числу $a$ , нужно: определить знак этого числа ; от начала координат отложить отрезок , равный $\left|a\right|$ вправо , если знак "+" и влево , если знак "-" .
Число $a$ в таком случае называют координатой построенной точки .
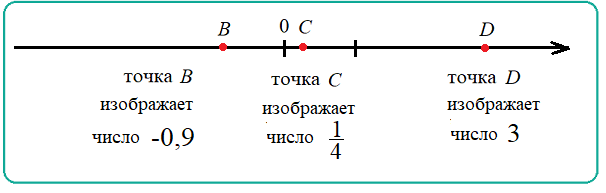
На рисунке числа $3$, $\frac{1}{4}$, $-0,9$ изображены соответсвенно точками $B$, $C$, $D$ . Числа - это «адреса» точек на координатной прямой. Точки - это "фотографии" чисел.
1) Выбрать на прямой начало координат ;
2) Выбрать положительное направление ;
3) Выбрать единичный отрезок.
Координаты точки:
Каждой точке можно присвоить свою координату - это расстояние от точки до начала координат с учетом знака: слева от $0$ знак $-$ , справа $+$.
Изображение числа :
пробa
По любой координате можно восстановить точку.




Расстояние от точки до начала отсчета на прямой.
Если нам известна координата точки , то мы можем сказать какое расстояние от этой точки до начала координат - точки $O$.
Если точка $A$ имеет координату $a$ , то расстояние между точками $A$ и $O$ равно длине отрезка $AO$ $=\left|a\right|$ . Например: если точка $A$ имеет координату $-5$ , $A(-5)$ $\Rightarrow $ $AO=5$ ; если точка $A(4)$ $\Rightarrow $ $AO=4$ .
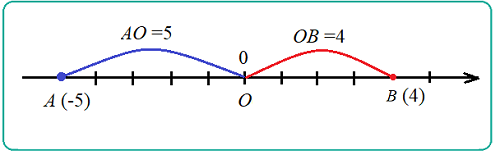
Расстояние между точками координатной прямой.
Пусть на прямой заданы две произвольные точки и их координаты известны , тогда между ними можно найти расстояние , т.е. длину отрезка , соединяющего эти точки. Как?
По специальной формуле: если точки $A$ и $В$ имеют соответсвенно координаты $a$ и $b$ , то - расстояние между двумя точками координатной прямой равно модулю разности их координат.
$$AB=\left|a-b\right|$$

{ОтступВниз:70:}
Упражнения С:
