- Прямоугольная система координат: положение точки определяется двумя её координатами - абcциссой и ординатой .
- Система координат: Абсцисса - ось $x$. Ордината - ось $y$.
- Точка $(2;-3)$: пересечение линий: горизонтальная линия $y = -3$ ; вертикальная линия $x = 2$
- Точка с координатами $(x;y)$ например, $(2;-3)$ : наносим точку, справа на 2 единицы, вниз на 3 единицы.
Алгоритм: детальное построение графика заданной функции
- вычислить значения функции: различные $x$ - числа подставить в выражение функции и найти свои $y$ - значения.
- составить таблицу: список точек ($x$; $y$ ), пары соответствующих $x$ - чисел и его $y$ - значений абсциссы и ординаты.
- нанести эти точки из списка на координатную плоскость в соответствии с координатами точек.
- построить график: линию, проходящую через все нанесенные точки. Аккуратно, красиво!
- при необходимости, дополнить список новыми точками: подобрать $x$ - числа для коррекции, уточнения графика.
Функция $y=f\left(x\right)$ - это правило, по которому $x$ - аргументам соответствуют у - значения.
- $x$ называется аргументом функции.
- $y$ переменная - значение функции при определенном аргументе.
- $f\left(x\right)$ - Правило, или закон функции - по которому вычисляются значения функции.
Пример 1: Построить график функции $y=-2x+7$
- У нас правило функции $f\left(x\right)=-2x+7$. Вычислим несколько значений для различных $x$ - аргументов:
- $f\left(0\right)=7$ $f\left(1\right)=-2+7=5$ $f\left(2\right)=-4+7=3$ $f\left(6\right)=-12+7=-5$
- или, можно писать так: $x=5$ $\Rightarrow$ $y=-10+7=-3$ $x=-3$ $\Rightarrow$ $y=6+7=13$ $x=-1$ $\Rightarrow$ $y=-2+7=5$
- Таблица значений: $(0;7)$ $(1;5)$ $(2;3)$ $(6;-5)$ $(5;-3)$ $(-3;13)$ $(-1;5)$
- Получили список точек, их координат. Таблица значений. Отметим точки на координатной плоскости. Проведем график.
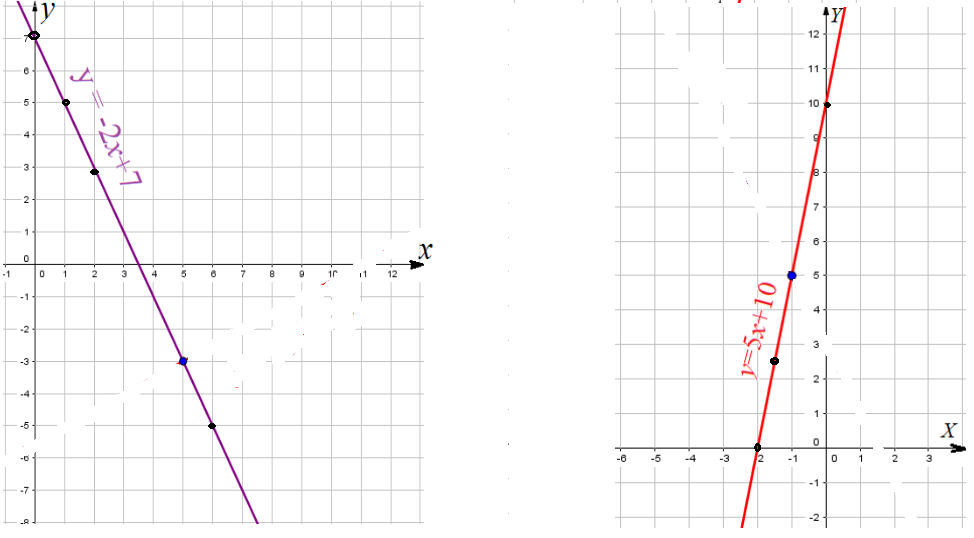
Пример 2: Построить график функции $y=5x+10$
- У нас правило функции $f\left(x\right)=5x+10$. Вычислим несколько значений для различных $x$ - аргументов:
- $f\left(-2\right)=0$ $f\left(-1,5\right)=-7,5+10=2,5$ $f\left(0\right)=10$ $f\left(1\right)=5+10=15$
- Таблица значений: $(-2;0)$ $(-1,5;2,5)$ $(-1;5)$ $(0;10)$ $(1;15)$
- Получили список точек, их координат. Таблица значений. Отметим точки на координатной плоскости. Проведем график.
Прямая, линейная функция, график
Линейной функцией называется функция вида $y=kx+b$ , где коэффициенты $k$ и $b$ - заданные числа.
- Графиком линейной функции является прямая линия.
- Т.к прямая определяется двумя её точками, то для построения графика функции достаточно построить две точки этого графика.
- Замечание: для построения графика $y=kx+b$ удобно находить точки пересечения с осями координат:
- Для $x=0$ найдем свой $y$ $\Rightarrow$ $y=b$. Точку $(0;b)$ с такими координатами отметим на оси ординат.
- Теперь, для $y=0$ найдем свой $x=-\frac{b}{k}$. Точка $(-\frac{b}{k};0)$ на абсциссе. Это и есть точки пересечения с осями.
При $b=0$ линейная функция имеет вид $y=kx$. Прямая проходит через начало координат.
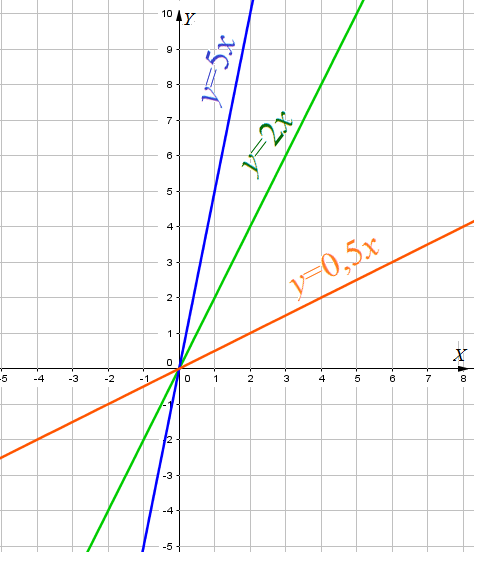
Cвойства функции y=kx при k > 0 (наклон прямой вправо)
- Свойство 1: Область Определения Функции - вся числовая прямая
- Свойство 2: Нули - $y=0$ при $x=0$ .
- Свойство 3: $y=kx$ - непрерывная функция.
- Свойство 4: Функция $y=kx$ возрастает на всей числовой оси.
- Свойство 5: Область значений функции $y=kx$ - все числа.
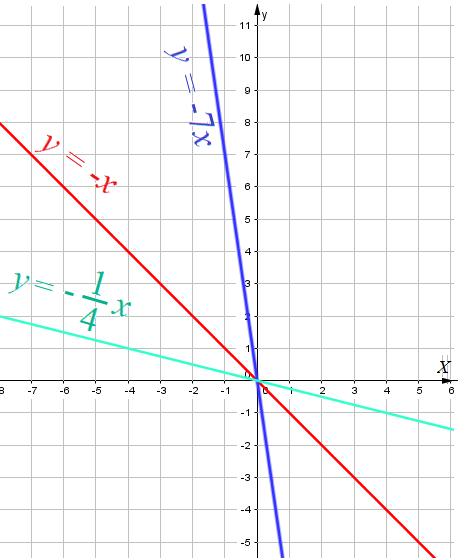
Cвойства функции y=-kx при k > 0 (наклон прямой влево)
- Свойство 1: Область Определения Функции - вся числовая прямая
- Свойство 2: нули - $y=0$ при $x=0$ .
- Свойство 3: $y=-kx$ - непрерывная функция.
- Свойство 4: Функция $y=-kx$ убывает на всей числовой оси.
- Свойство 5: Область значений функции $y=-kx$ - все числа.
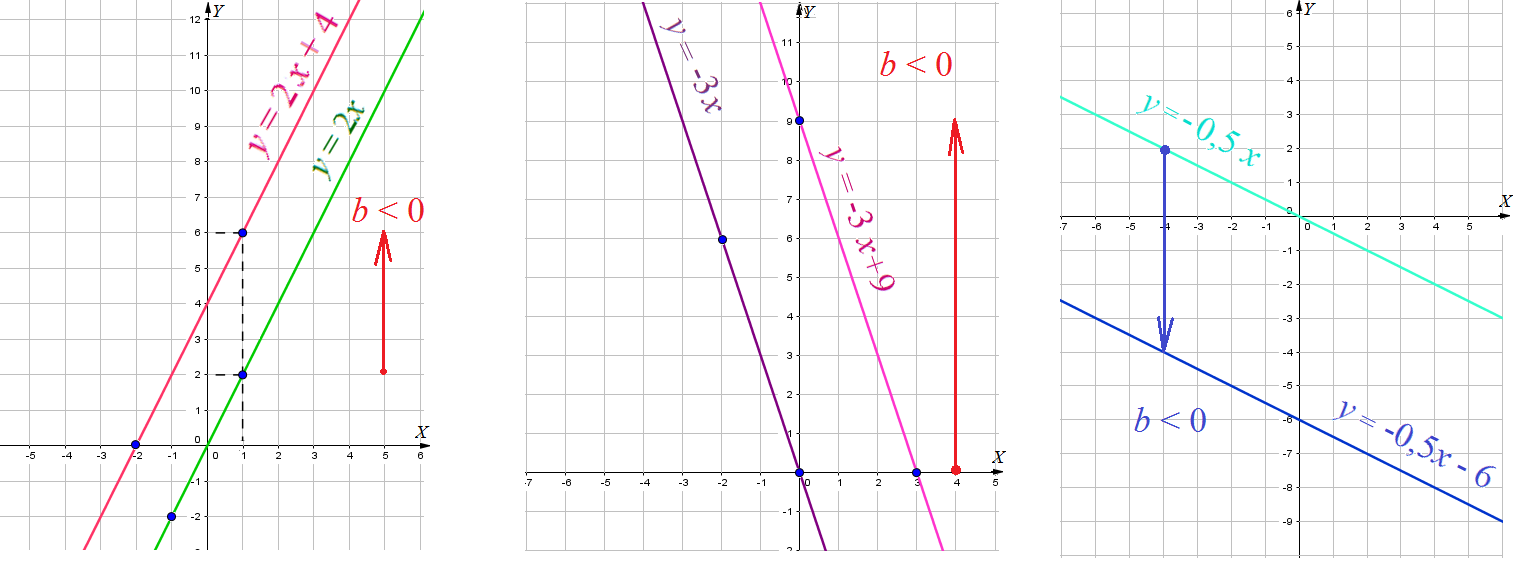
Графиками функций $y=kx+b$, $y=k(x+c)$ и $y=kx$ являются параллельные прямые.
График функции $y=kx+b$ получается сдвигом графика функции $y=kx$ на $b$ единиц вдоль оси ординат.
- Если $b$ положительно, то сдвиг вверх. Если же отрицательно, то вниз.
График функции $y=k(x+c)$ получается сдвигом графика функции $y=kx$ на $-c$ единиц вдоль оси ординат
- Если $c$ положительно, то сдвиг влево. Если же отрицательно, то вправо.
Графическое решение уравнений
Наклон графика определяется $k$ - коэффициентом функции $y=kx+a$ при $x$. чем меньше $k$ - коэффициент, тем "горизонтальнее".
Параллельность: линейные функции $y=kx+a$ и $y=kx+b$ имеют одинаковые $k$ - коэффициент наклона, то их графики - прямые параллельны.
Перпендикулярность: графики прямых $y=kx+a$ и $y=-\frac{1}{k}x+b$ взаимоперпендикулярны, произведение коэффициентов наклона равен $-1$.
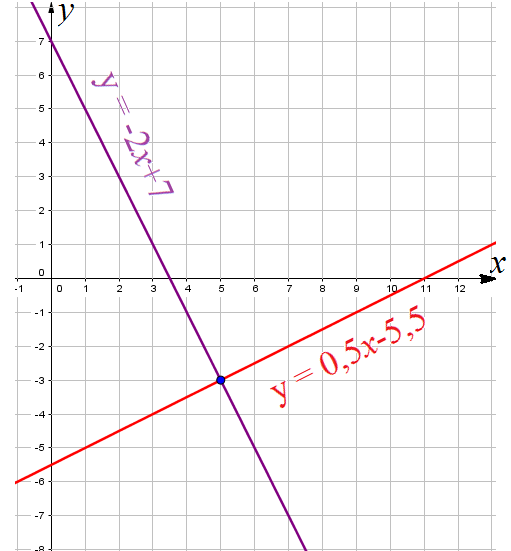
Пример 3: Решить уравнение $-2x+7=0,5x-5,5$ графическим способом.
- Построим прямые $y=-2x+7$ и $y=0,5x-5,5$. По чертежу найдем точку пересечения графиков
- $\left(5;-3\right)$. абсцисса этой точки является корнем данного уравнения,
- потому что, именно для этого $x$ значения
- графиков, а значит и функций, значения левой и правой частей выравниваются. ответ: $x=5$.
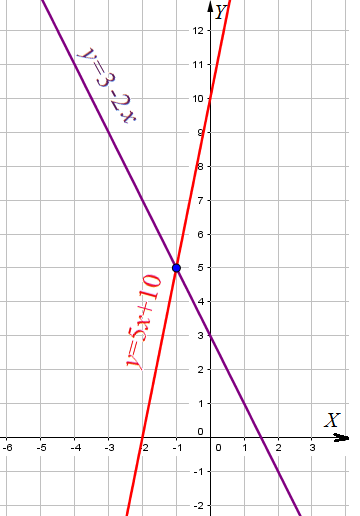
Пример 4: Решить систему уравнений { $2x+y=3$; $y-5x=10$ }
- Преобразуем первое уравнение системы к виду $y=3-2x$, второе уравнение системы к виду $y=5x+10$
- по чертежу найдем точку пересечения графиков: $\left(-1;5\right)$. Координаты этой точки и являются решением системы.
- При таких $x$ и $y$ оба уравнения системы выравниваются, значит такое решение удовлетворяет уравнение.
- ответ: $x=-1$ ; $y=5$
Пример 5: Найти $b$, если известно, что график $y=\frac{7}{9}x+b$ проходит через точку $\left(-9;-3\right)$
- Какое число $b=?$, если при аргументе $x=-9$ функция имеет значение $y=-3$ ? Запишем это в виде условия.
- Координаты заданной точки $x=-9$ , $y=-3$. Подставим в уравнение функции эти значения:
- $-3=\frac{7}{9}\left(-9\right)+b$ получим $-3+7=b$ $\Rightarrow$ $b=4$ ответ: $b=4$ , линейная функция $y=\frac{7}{9}x+4$.
Линейная функция и ее график. Правила.
Линейное уравнение имеет вид $ax + by + c = 0$ . Линейная функция имеет вид $y=kx+m$
- Например: $5x–4y+6=0$ . Выразим $y$: $4y=5x+6$ разделим на $4$ : $y=\frac{5x+6}{4}$ $\Rightarrow$ $y=1,25x+1,5$ .
- Полученное уравнение, равносильно первому, имеет вид $y=kx+m$ , где: $k$ и $m$ — коэффициенты (параметры).
- $x$ — независимая переменная - аргумент функции;
- $y$ — зависимая переменная - значение функции;
- Функцию, зависимую переменную $y$ принято заменять буквой $f$ или $p$, с указанием аргумента в скобках — $f(x)$ или $p(x)$
- Например: $f(x) = 1,25x + 1,5$ , $p(x) = kx + m$ , функция $1,25x + 1,5$ или функция $kx + m$ .
- Под словом функция мы подразумеваем как переменную $y$ , так и всё выражение в правой части уравнения.
Построение графика линейной функции сводится к нахождению координат двух точек, так как её график — прямая.
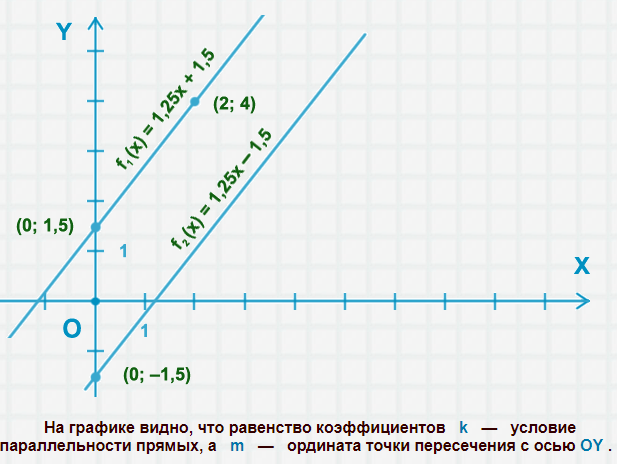
Пример 6: Построим графики двух функций: $f_1(x)=1,25x + 1,5$ и $f_2(x)=1,25x–1,5$ .
- Первая точка $f_1(0) = 1,5$ : $x=0$ ; $y=1,5$ т. к. $y=1,25x+1,5$ $\Rightarrow$ $y=1,25\cdot0+1,5=1,5$ .
- Вторая точка $f_1(2) = 4$ : $x=2$ ; $y=4$ т. к. $y=1,25x+1,5$ $\Rightarrow$ $y=1,25\cdot2+1,5=4$ .
- График $f_2$ строим аналогично.
Упражнения: