Уравнение касательной к графику функции в данной точке

Производная функции показывает скорость изменения функции в точке, тангенс угла наклона.
Производная числа (т.е. функция = числу) равна нулю. Число - постоянная функция никак не изменяется!

Производная vs касательная к графику функции.

Приближенное и точное определение производной функции

Приближенным значением производной функции в точке $x_{0}$ со сдвигом 0,01 называется значение

$f'\left(x_0\right)\approx \frac{f\left(x_0+0,01\right)-f\left(x_0\right)}{\left(x_0+0,01\right)-\left(x_0\right)}$ $f'\left(a\right)\approx \frac{f\left(a+h\right)-f\left(a\right)}{\left(a+h\right)-\left(a\right)}$ Точное: $f'\left(x_0\right)=\lim_{h\to 0} \frac{f\left(x_0+h\right)-f\left(x_0\right)}{\left(x_0+h\right)-\left(x_0\right)}$

Производная в точке - это отношение: (приращение самой функции) / (малое приращение аргумента в этой точке).
Физический смысл - производная функции показывает скорость изменения функции: роста или убывания функции.
Геометрический смысл - производная в каждой точке равна тангенсу угла наклона касательной, проведенной к ее графику.

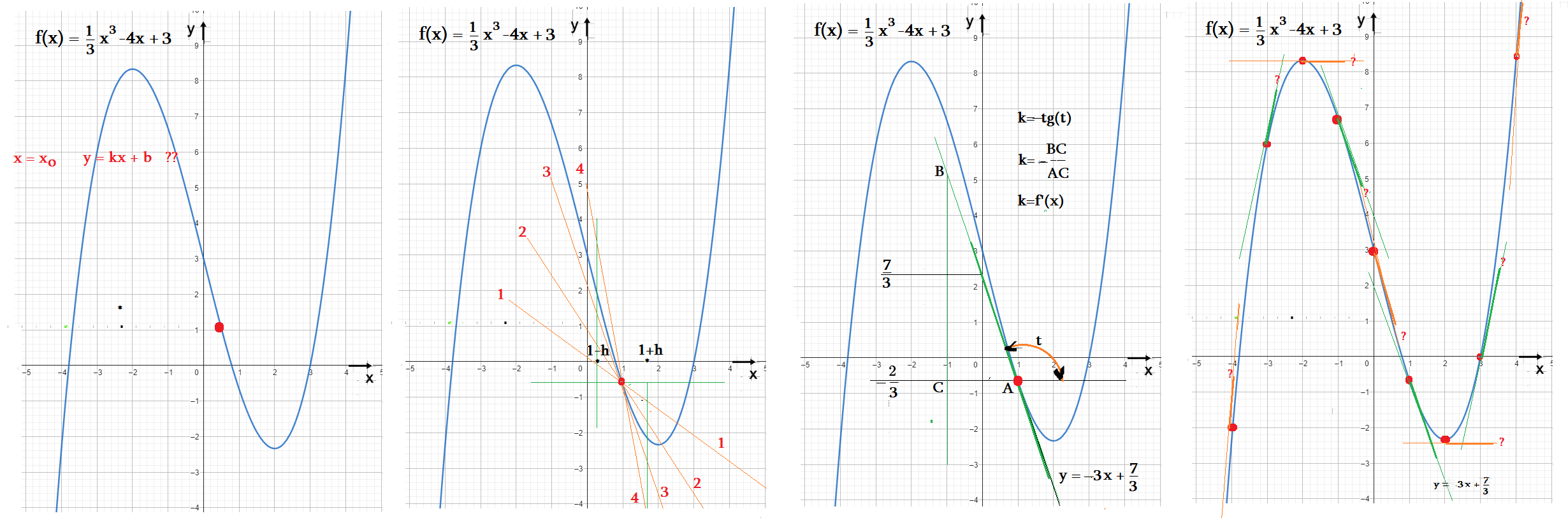
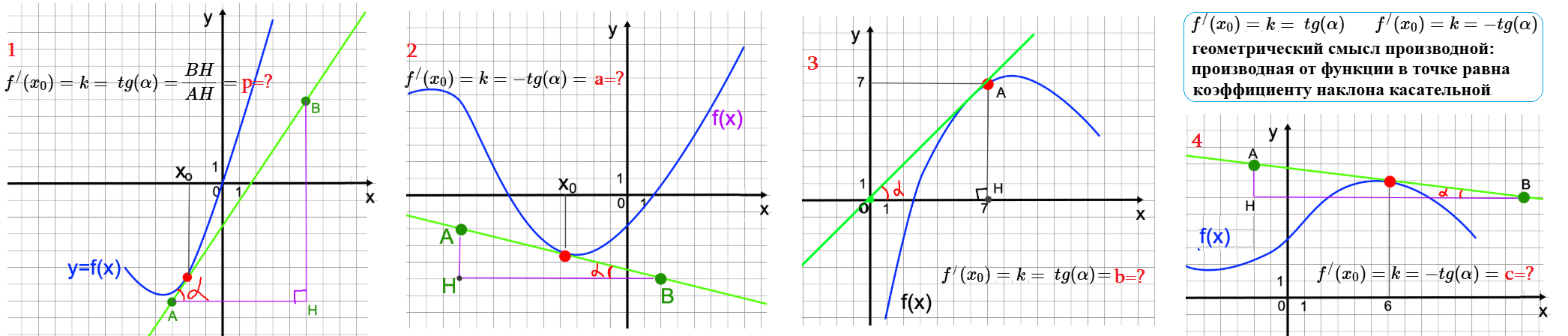
Задача 1: На рисунке изображен график функции $f(x)$ и касательная к этой функции в точке $x_0$. Найдите значение производной функции $f'(x)$ в точке $x_0$.

Геометрический смысл производной: производная от функции в точке равна коэффициенту наклона касательной, проведенной к этой точке.
Тангенс угла наклона касательной к горизонтали и будет равен производной функции в точке $x_0$.
Нахождение тангенса: достроим касательную до прямоугольного треугольника $ABH$.
Отметим такие точки, чтоб стороны треугольника получались целыми: $AH$ равна 8 клеточкам, а $BH$ равна 12 клеточкам.
Найдем значение тангенса $\alpha$: $\tg \alpha=\frac{BH}{AH}=\frac{12}{8}=\frac{3}{2}$ Ответ: $f'(x)=\tg \alpha=1,5$

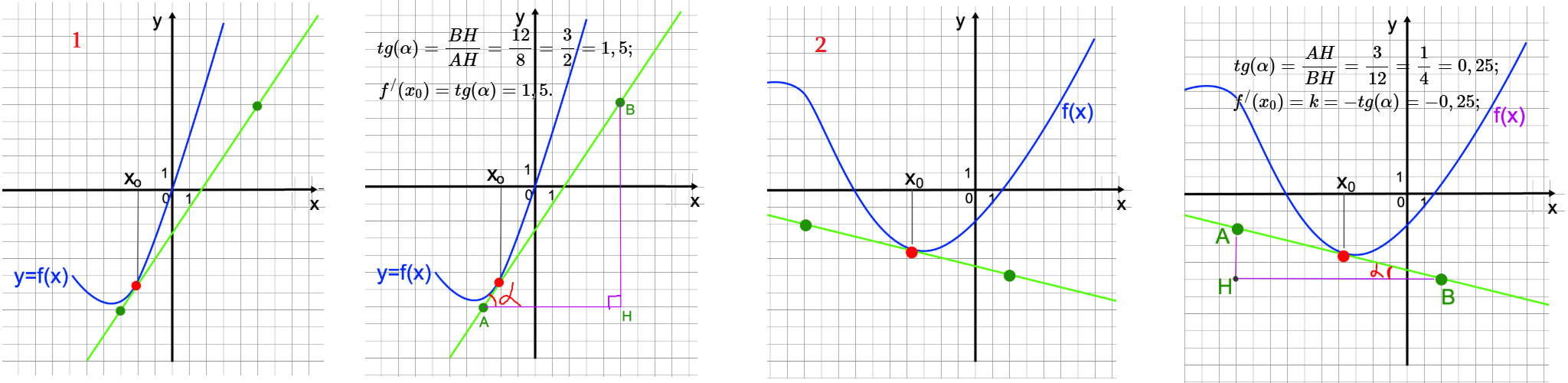
Задача 2: На рисунке изображен график функции $f(x)$ и касательная к этой функции в точке $x_0$. Найдите значение производной функции $f'(x)$ в точке $x_0$.

аналогично №1. Достроим касательную до прямоугольного треугольника, выберем удобные целые точки.
Находим тангенс α - наклон касательной к горизонтальному катету: $\tg \alpha=\frac{BH}{AH}=\frac{3}{12}=0,25$
Здесь есть один ньюанс (нельзя ошибаться): касательная - это прямая, идущая сверху вниз. Значит, убывает.
У таких прямых коэффициент наклона всегда отрицательный: $k=-\tg \alpha$
Значит и производная в точке $x_0$ тоже должна быть отрицательна: $f'(x)=k=-\tg \alpha=-0,25$ Ответ: $-0,25$

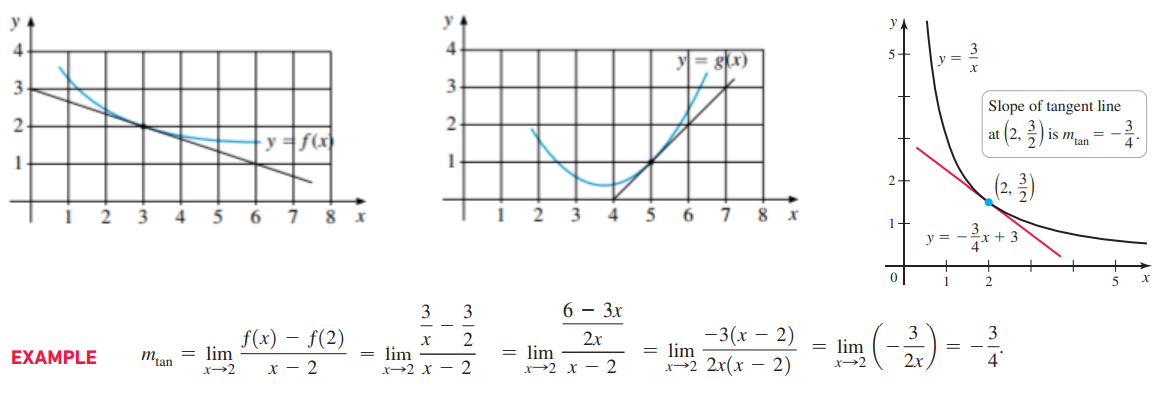
Задача 3: На рисунке изображен график некой функции $y=f\left(x\right)$ и касательная в заданной точке. Найти значение производной в указанной точке $x_0=3$.

Как по клеточкам найти производную? Ищем коэффициент наклона касательной в указанной точке $x=x_0$.
Смотрим на касательную - прямую, касающуюся с графиком $f\left(x\right)$ в точке $x_0=3$ .
Тангенс угла наклона ... надо увидеть прямоугольный треугольник с катетами вдоль х- и у-, и с гипотенузой по касательной:
Считаем по клеткам: f'(3) = - 1 : 3 1 клетка по у - оси вниз (-), 3 клетки по х - оси вправо (+) .
На 2-м рисунке: g'(5) = 2 : 2 2 клетки по у - оси вверх (+), 2 клетки по х - оси вправо (+) .

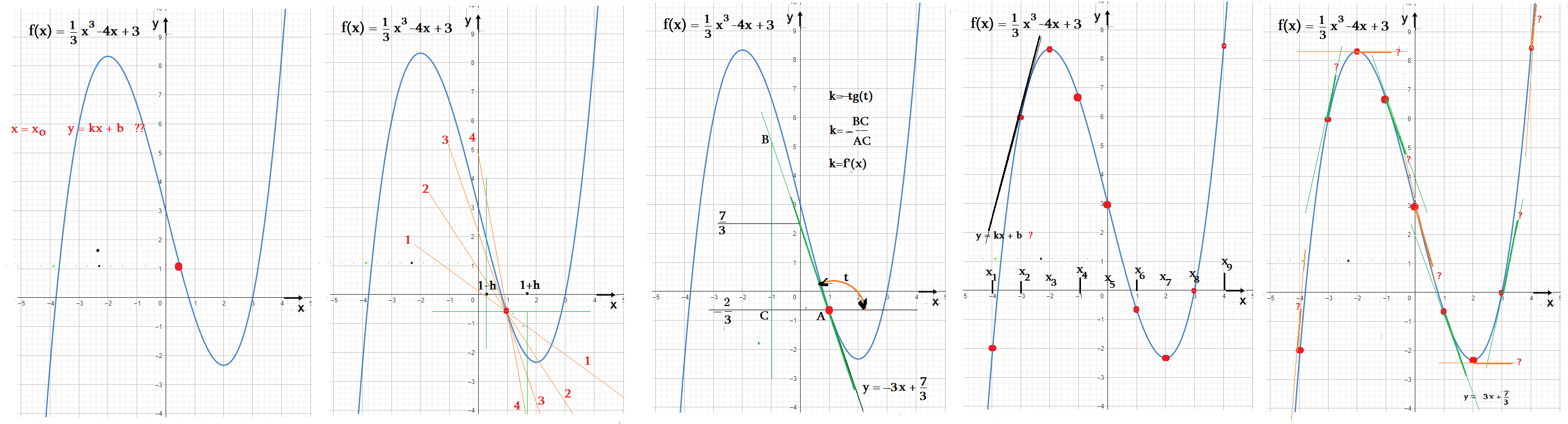
Уравнение касательной к графику в заданной точке

Уравнение касательной функции $y=f\left(x\right)$ в точке $x=x_0$ : $y=f\left(x_0\right)+f'\left(x_0\right)\cdot\left(x-x_0\right)$

касательная, прямая, линейная функция y = kx + b, коэфф: $k=f'\left(x_0\right)$, $b=f\left(x_0\right)-f'\left(x_0\right)\cdot x_0$

Прямая $y=f\left(x_0\right)+f'\left(x_0\right)\cdot\left(x-x_0\right)$ в точке $x=x_0$ касается графика функции $y=f\left(x\right)$.
Функция $y=f\left(x\right)$ и её касательная $y=kx+b$ в точке касания $x=x_0$ имеют одинаковые значения, наклон, производные.
Наклон касательной = производное функции $k=f'\left(x_0\right)$ определяет как "течет" график: растет, убывает?
$k>0$ : наклон касательной положительный - касательная слева-направо - чем правее $x$, тем выше поднимается прямая.
$k>0$ $\Rightarrow$ $f'\left(x_0 \pm \delta \right)>0$ - производная положительна - функция около $\left(x_0-\delta;x_0+\delta\right)$ растет - график поднимается вверх.
Наклон отрицательный, $k<0$ - касательная справа-налево - производная отрицательна - функция убывает - график "течет" вниз.

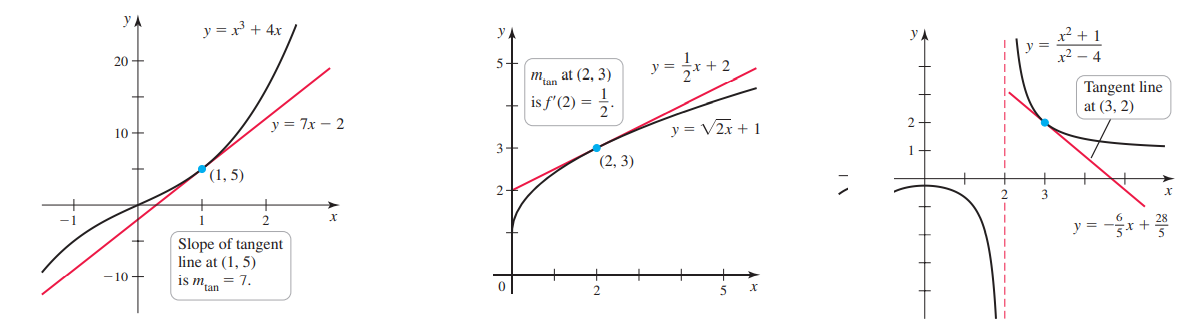
Задача 4: Найти уравнение касательной для $f\left(x\right)=x^3-3x+2$ в точках $x=0.5$ и $x=-2$ .

$f\left(x\right)=x^3-3x+2$ функция
$\left(x^3-3x+2\right)'=3x^2-3$ находим производную от функции
$f\left(0,5\right)=0,5^3-3\cdot 0,5+2=0,625$ значение функции в точке $x=0.5$
$f'\left(0,5\right)=3\cdot 0,5^2-3=-2,25$ значение производной функции в точке $x=0.5$
$x=0.5$ $y=f\left(0,5\right)+f'\left(0,5\right)\cdot \left(x-0,5\right)$ формула уравнения касательной в $x=0.5$
$x=0.5$ $y=0,625-2,25\cdot \left(x-0,5\right)$ составляем уравнение касательной в точке $x=0.5$
$x=0.5$ $y=-2,25\cdot x +1,75$ упростим уравнение касательной, по форме линейной функции.
$f\left(-2\right)=(-2)^3-3\cdot (-2)+2=0$ значение функции в точке $x=-2$
$f'\left(-2\right)=3\cdot (-2)^2-3=9$ значение производной функции в точке $x=-2$
$x=-2$ $y=f\left(-2\right)+f'\left(-2\right)\cdot \left(x-(-2)\right)$ формула уравнения касательной в $x=-2$
$x=-2$ $y=0+9\cdot \left(x+2\right)$ составляем уравнение касательной в точке $x=-2$
$x=-2$ $y=9\cdot x+18$ упростим уравнение касательной, форма линейной.

Комментарий: Посмотрим ... являются ли полученные прямые касательными в заданных точках. $x=0.5$ значение $y=0,625$, наклон $y'=-2,25$. Совпадают $y=-2,25\cdot x +1,75$ и $f\left(x\right)$ в этой точке: и значению и наклон. $x=-2$ значение касательной $y=0$, коэффициент наклона $y'=9$. Есть касание $y=9\cdot x+18$ и функции $f\left(x\right)$.

Задача 5: Прямая $y=1-5x$ параллельна некой касательной к графику функции $f\left(x\right)=4x^3-8x$. Найдите координаты точек касания таких касательных.

$f\left(x\right)=4x^3-8x$ функция , $G_f$ - ее график
$\left(1-5x\right)'=-5$ коэффициент наклона прямой
$\left(4x^3-8x\right)'=12x^2-8$ производная функция, $f'\left(x\right)$
$12x^2-8=-5$ $12x^2=3$ $x=0,5$ $x=-0,5$ производное = наклону: , корни.
$f'\left(0,5\right)=-5$ $f'\left(-0,5\right)=-5$ значения наклонов в этих точках
$f\left(0,5\right)=4(0.5)^3-8(0.5)=4(0.125)-4=-3.5$ . значение функции при $x=0,5$
$x_1=0,5$ $y=-3,5-5(x-0,5)$ $y=-5x+6$ уравнение касательной при $x=0,5$
$G_f$ $(0,5;-3,5)$ точка касания, на графике функции $f\left(x\right)$
$f\left(-0,5\right)=4(-0.5)^3-8(-0.5)=-4(0.125)+4=3.5$ значение функции при $x=-0,5$
$x_2=-0,5$ $y=-3,5-5(x+0,5)$ $y=-5x-6$ уравнение касательной при $x=-0,5$
$G_f$ $(-0,5;3,5)$ координаты точки касания

Комментарий: 1. Мы нашли наклон прямой $y=1-5x$, равен $-5$. Раз прямая параллельна касательной $\Rightarrow$ и касательная должна иметь такой же наклон, $\Rightarrow$ производная = -5 2. $\Rightarrow$ поэтому составляем уравнение $f'\left(x\right)=-5$ ... и, решая, узнаем где наклон станет $-5$. 3. Вычислим в этих точках ( $x=0,5$, $x=0,5$) значения функции, чтоб найти координаты точек касания. 4. Зная значение функции и производной, можем расписать уравнение касательной. Мы получили два касательных $y=-5x+6$, $y=-5x-6$ в двух точках. 5. Очевидно, что эти прямые действительно параллельны заданной прямой $y=1-5x$ ... ибо коэффициент перед $x$ у всех $-5$ $\Rightarrow$ наклон одинаковый $\Rightarrow$ эти прямые параллельны. Как и требовалось по условию задачи.

Какой наклон у функции $y=1-5x$ ? Какая производная? Конечно, $-5$.
Параллельная ему наша касательная к функции $y=4x^3-8x$ должна иметь такой же наклон $-5$.
$\left(4x^3-8x\right)'=12x^2-8$ найдем производное нашей функции: штрих по х.
В каких точках $x$ значение производной равно $-5$? Составим уравнение и найдем такие $x$ !
Условие для касательной: $12x^2-8=-5$ $12x^2=3$ $x^2=\frac{1}{4}$ , корни: $x=0,5$ $x=-0,5$
При $x=0,5$ значение нашей функции $y=4(0.5)^3-8(0.5)=4(0.125)-4=-3.5$ . Значит, точка касания $(0,5;-3,5)$.
При $x=-0,5$ значение нашей функции $y=4(-0.5)^3-8(-0.5)=-4(0.125)+4=3.5$ . Значит, точка касания $(-0,5;+3,5)$.

Функции с параметром: производная, касательная

Функция $y=-2x^2-mx-4$ Обозначение: $y'=p$ - производная функции.

$y$ - функция, зависимая переменная от независимой перемененной $x$. Для каждого $x$ определяется свой $y$.
$m$ - параметр, входящий в выражении функции. Постоянное, "пока что нам неизвестное", но число. Не изменяется, константа.
$p=y'$ - удобное обозначение, чтоб не писать $y'$. В данном случае $p=-4x-m$, производное от $-2x^2-mx-4$
Дифференцирование при параметре: $\left(-2x^2-mx-4\right)'=-4x-m$ - при штриховании параметр воспринимаем как число: $m'=0$
$y=kx+b$ касательная прямая к графику функции $y=-2x^2-mx-4$. $k$ - коэффициент наклона касательной.
условие о касательности: в точке $x$: $kx+b=-2x^2-mx-4$, $k=p$ т.е. $k=y'$ - коэффициент = производной.
комментарии: Что такое касательная прямая к графику функции в точке $x_0$ ? Касательная должна проходить в той же точке системы координат, что и график функции. Значит, числовые значения касательной и функции должны быть равными при данном $x=x_0$. Кроме того, касательная должна касаться графика, т.е. у них должны быть одинаковые наклоны, т.е. коэффициент наклона касательной должен быть равен производной функции в точке $x=x_0$. Итого: касательная и функция должны совпадать как по значениям так и по производным

Задача 6: Прямая $y=3x+4$ является касательной к графику функции $y=-2x^2-mx-4$.

Найти $m$, если известно, что точка касания имеет отрицательную абсциссу.

$p=-4x-m$ производная от параметрической функции, $p=y'$
$(3x+4)'=3$ $k=3$ коэффициент наклона касательной
$-4x-m=3$ равенство значений производной функции и наклона касательной: $p=k$
$-2x^2-mx-4=3x+4$ равенство значений функции и касательной в точке касания $x$.
$-4x-m=3$ $-2x^2-mx-4=3x+4$ получим систему уравнений из 2-х неизвестных $m$, $x$.
$m=-4x-3$ $-2x^2+\left(4x+3\right)x-4=3x+4$ выразим неизвестное и подставим во 2-ое уравнение.
$2x^2=8$ $x=-2$ Решим уравнение и выбираем отрицательный корень.
$x=-2$ $m=-4x-3=5$ $m=5$ При выбранной абсциссе получим значение параметра.

Теорема о касании: Если графики двух функций $f\left(x\right)$ и $g\left(x\right)$ касаются друг друга, то в точке касания $x_0$:

$f\left(x_0\right)=g\left(x_0\right)$ $f'\left(x_0\right)=g'\left(x_0\right)$ , значения функций и также значения их производных совпадают.

Уравнение касательной к графику функции $y=f\left(x\right)$ в точке $x=x_0$ : $y=f\left(x_0\right)+f'\left(x_0\right)\cdot\left(x-x_0\right)$ - касательная, прямая

Решаем устно: