Что такое функция и что такое сложная функция ?
Что такое функция и что такое сложная функция ?
- Функция $g\left(t\right)=3\cdot t-1$ - это правило отображения $t$ - чисел в значения функции $g\left(.\right)$ по указанному правилу.
- Например: числу $t=2$ соответствует значение $g\left(2\right)=3\cdot 2-1=5$. "2" отображается в "5".
- Еще: $t=0$ отображается в $-1$, т.е. $g\left(0\right)=-1$ ; говорят: функция $g$ в точке $0$ принимает значение $-1$.
- Именно все такие пары соответствий $\left(2;5\right)$ , $\left(0;-1\right)$ , $\left(4;11\right)$ ... все прочие "делают" функцию.
- "Я знаю кто он, если я знаю на что он способен, что и как он делает". Функция: аргумент $\to$ значение
- $g\left(t\right)$ переводит значения аргументов в значения функции. Имя аргумента " $t$ " здесь не важно, важно правило: $3\cdot t-1$ !
- Другая функция, $f\left(z\right)=z^2$ переводит, отображает 5 ---> 25, -1 ---> 1. т.е. $f\left(5\right)=25$ $f\left(-1\right)=1$
- Ключевые термины: функция имя аргумент правило вычисления значения
- $g\left(t\right)$ $g\left(t\right)=3\cdot t-1$ $g$ $t$ $3\cdot t-1$
- $f\left(z\right)$ $f\left(z\right)=z^2$ $f$ $z$ $z^2$
Сложная функция $f\left(g\left(x\right)\right)=\left(3x-1\right)^2$ комбинированная из двух: $f$ и $g$
- для $x=2$ функция $f\left(g\left(2\right)\right)=f\left(5\right)=25$, значение по правилу такое же $\left(3\cdot 2-1\right)^2=25$
- для $x=0$ функция $f\left(g\left(0\right)\right)=f\left(-1\right)=1$, также и значение по правилу $\left(3\cdot -1-1\right)^2=1$
- термины $f\left(g\left(x\right)\right)$ $x$ - аргумент функции $g$. $g\left(x\right)$ - аргумент функции $f$.
- $f$ - внешняя функция, $g$ - внутренняя функция. Правило сложной функции $\left(3x-1\right)^2$
- $f\left(g\left(x\right)\right)=f\left(3x-1\right)=\left(3x-1\right)^2=\left(g\left(x\right)\right)^2$ ... $x$ (по правилу $g$ ) ---> $\left(3x-1\right)$ (по правилу $f$) ---> $\left(3x-1\right)^2$
Задача 1: Найти производную сложной функций $\left(\left(3x-1\right)^2\right)'$
- Сложная функция: внутренняя $g\left(x\right)=3x-1$ и внешняя $f\left(g\right)=\left(g\left(x\right)\right)^2$ - квадрат от аргумента, от внутренней
- Метод Замены: Введем новую переменную $X=3x-1$ ... "внутренняя функция стала переменной от $x$ "
- Итак, зависимости: $f\left(X\right)=\left(X\right)^2$, $X=3x-1$ . C какой скоростью изменяется $f$ при изменении $x$ ?
- выражение $\left(X\right)^2$ при изменениях $X$ изменяется со скоростью $\left(\left(X\right)^2\right)'=2\cdot X=2\cdot (3x-1)$
- переменная $X$ при изменениях аргумента $x$ изменяется со скоростью $\left(X\right)'=\left(3x-1\right)'=3$
- тогда, "комбинация двух изменений": $\left(X\right)^2$ при изменениях $x$ меняется по умножения скоростей $2\cdot (3x-1)\cdot 3$
- иллюстрация правила умножения: Проследим за всеми взаимными изменениями
- $\bigtriangleup \left(X^2\right)\approx \left(X^2\right)'\cdot \bigtriangleup X=\left[2X\right]\cdot \bigtriangleup X$ $\bigtriangleup X\approx \left(X'\right)\cdot \bigtriangleup x=\left(3x-1\right)'\bigtriangleup x$
- комбинированная скорость $f'\left(x\right)\approx \frac{\bigtriangleup \left(X^2\right)}{\bigtriangleup x}=\frac{\bigtriangleup \left(X^2\right)}{\bigtriangleup X}\cdot \frac{\bigtriangleup \left(X\right)}{\bigtriangleup x}\approx \left[2X\right]\cdot \left(X'\right)=\left[2\cdot \left(3x-1\right)\right]\cdot \left(3\right)$ - умножение скоростей
Решение: Оформим записи о дифференцировании сложной функции через равенства - действия шаг за шагом:
$\left(\left(3x-1\right)^2\right)'=\left(X^2\right)'\cdot X'=2X\cdot X'=2\left(3x-1\right)\cdot \left(3x-1\right)'=2\left(3x-1\right)\cdot 3=18x-6$. Или, короче:
$\left(\left(3x-1\right)^2\right)'=2\left(3x-1\right)\cdot \left(3x-1\right)'=2\left(3x-1\right)\cdot 3=18x-6$ (замена $X=3x-1$ в воображении)
Хорошие вопросы: Производная Чего? в этом случае "квадрата". Что есть внешняя и что есть внутренняя функции?
Теорема: Производная Сложной Функции по аргументу $x$ равна умножению
производной внешней функции по внутренней на производной внутренней функции по $x$.
$\left(f\left(g\left(x\right)\right)\right)'=f_g'\cdot g_x'$ Метод Замены: $\left(f\left(g\left(x\right)\right)\right)'=\left(f\left(X\right)\right)'=f_X'\left(X\right)\cdot X'$.
$X=g\left(x\right)$ - внутреннее выражение. Доказательство через осмысление предела: $\frac{\bigtriangleup f\left(g\left(x\right)\right)}{\bigtriangleup x}=\frac{\bigtriangleup f\left(g\right)}{\bigtriangleup g}\cdot \frac{\bigtriangleup g\left(x\right)}{\bigtriangleup x}$
Таблица Основных Производных ... $X$ большое - любое выражение от $x$, внутренная функция:
-
Степень: $\left(X^n\right)'=n\cdot X^{n-1}\cdot X'$ $\left(X^3\right)'=3X^2\cdot X'$
-
Корень: $\left(\sqrt{X}\right)'=\left(X^{\frac{1}{2}}\right)'=\frac{1}{2}\cdot X^{-\frac{1}{2}}\cdot X'$ $\left(\sqrt[3]{X}\right)'=\left(X^{\frac{1}{3}}\right)'=\frac{1}{3}\cdot X^{-\frac{2}{3}}\cdot X'$
-
Тригонометрические: $\left(\sin X\right)'=\cos X\cdot X'$ $\left(\cos X\right)'=-\sin X\cdot X'$
-
Экспоненциальные: $\left(e^X\right)'=e^X\cdot X'$ $\left(a^X\right)'=a^X\cdot \ln a\cdot X'$
-
Логарифмические: $\left(\ln X\right)'=\frac{1}{X}\cdot X'$ $\left(\log _aX\right)'=\left(\frac{\ln X}{\ln a}\right)'=\frac{1}{X\cdot \ln a}\cdot X'$
Правила Дифференцирования:
-
производная суммы равна сумме производных: $\left(A-B+C\right)'=A'-B'+C'$
-
правило производной от умножения: $\left(A\cdot B\right)'=A'\cdot B+A\cdot B'$
-
правило производной от деления: $\left(\frac{A}{B}\right)'=\frac{A'\cdot B-A\cdot B'}{B^2}$
-
производная сложной функции : $\left(f\left(X\right)\right)'=f'\left(X\right)\cdot\left(X\right)'$
Дифференцирование "сложных" функций, ... ... "как замена" и умножение на производную "замены":
- Производная сложной функции ... в аргументе функции выражение от $x$, называем "заменой" $X$ :
- $\left(f\left(X\right)\right)'=f'\left(X\right)\cdot\left(X\right)'$. В сложных функциях надо распознать и выделить внешнюю и внутреннюю функцию.
- Найти производную внешней функции и умножить на производную внутренней функции.
- f- внешняя функция, $X$ - внутренняя. $f'\left(X\right)$ - производная в $X$ !
Главный вопрос при дифференцировании:
- Что находится под производным? $\left(....\right)'$ Штрих чего мы ищем?
- Варианты: умножение, деление, сумма, умножение на число, функция.
- Если функция, то какая? квадрат, степень, тригонометрия, экспоненциальная, логарифм, корень?
- Если квадрат, то чей? Если логарифм, то от чего? Если тригонометрия, то от какого аргумента?
Задача 2: Найти производные "сложных" функций
В сложных функциях важно правильно распознать внешнюю и внутреннюю функцию. И, перемножить их производные.
A. $\left(\sin7x\right)'=\left(\sin X\right)'=\cos X\cdot\left(X'\right)=\cos7x\cdot\left(7x\right)'=7\cos7x$
B. $\left(\sqrt{5\cdot x^2-6}\right)'=\left(\sqrt{X}\right)'=\frac{1}{2\sqrt{X}}\cdot\left(X\right)'=\frac{1}{2\sqrt{5\cdot x^2-6}}\cdot\left(5\cdot x^2-6\right)'=\frac{10x}{2\sqrt{5\cdot x^2-6}}=\frac{5x}{\sqrt{5\cdot x^2-6}}$
C. $\left(e^{-5x}\right)'=\left(e^X\right)'=e^X\cdot\left(X\right)'=e^{-5x}\cdot\left(-5x\right)'=-5e^{-5x}$
D. $\left(\cos\sqrt{5\cdot x^2-6}\right)'=\left(\cos X\right)'=-\sin X\cdot\left(X\right)'=-\sin\sqrt{5\cdot x^2-6}\cdot\left(\sqrt{5\cdot x^2-6}\right)'=-\frac{5x\cdot\sin\sqrt{5\cdot x^2-6}}{\sqrt{5\cdot x^2-6}}$
E. $\left(\log_3\left(x^5-3x^2\right)\right)'=\left(\log_3X\right)'=\left(\frac{\ln X}{\ln3}\right)'=\frac{1}{\ln3\cdot X}\cdot\left(X\right)'=\frac{1}{\ln3\cdot\left(x^5-3x^2\right)}\cdot\left(x^5-3x^2\right)'=\frac{5x^4-6x}{\ln3\cdot\left(x^5-3x^2\right)}$
Задача 3: Найти производную $\left(\sqrt{3x}\cos\left(4x+1\right)\right)'$
- перед нами произведение двух функций , возьмем производную от умножения по формуле
- $\left(fg\right)'=f'g+fg'$ : $\left(\sqrt{3x}\right)'\cos\left(4x+1\right)+\sqrt{3x}\left(\cos\left(4x+1\right)\right)'$ .
- функции , от которых предстоит взять производную, являются сложными .... производные сложных?
- важно правильно распознать, какая функция будет внешней, а какая внутренней для каждой сложной функции.
- $\sqrt{3x}$ : внешняя функция - квадратный корень ; внутренняя - выражение под корнем $3x$ , берем производную:
- $\left(\sqrt{3x}\right)'=\frac{1}{2}\left(3x\right)^{\frac{1}{2}-1}\cdot\left(3x\right)'=\frac{1}{2}\left(3x\right)^{-\frac{1}{2}}\cdot3=\frac{3}{2\sqrt{3x}}$
- $\cos\left(4x+1\right)$ : внешняя функция - тригонометрическая cos ; внутренняя - аргумент косинуса $4x+1$
- $\left(\cos\left(4x+1\right)\right)'=-\sin\left(4x+1\right)\cdot\left(4x+1\right)'=-\sin\left(4x+1\right)\cdot4x'=-4\sin\left(4x+1\right)$
- соберем все наши выкладки и получим производную исходного выражения:
- $\left(\sqrt{3x}\right)'\cos\left(4x+1\right)+\sqrt{3x}\left(\cos\left(4x+1\right)\right)'=\frac{3}{2\sqrt{3x}}\cos\left(4x+1\right)-4\sqrt{3x}\sin\left(4x+1\right)$
Chain rule Дииференцирование сложных функций
Задача 4: Найти производную "сложной" функций $e^{4-3x}$
- $\left(e^{4-3x}\right)'=$
- $y\sim 4-3x$ замена внутренней
- $\left(e^y\right)'=e^y \cdot \left(y\right)'$ (внешняя)'
- $\left(e^{4-3x}\right)'=e^{4-3x} \cdot \left(4-3x\right)'=$ формула сложности
- $\left(4-3x\right)'=\left(4\right)'-(3x)'=-3$ (внутренняя)'
- $\left(e^{4-3x}\right)'=e^{4-3x} \cdot (-3)=-3 e^{4-3x}$ (сложная)'
Комментарии: 1. Распознаем: $e^y$ - внешняя, ... $4-3x$ - внутренняя. 2. правило замены: $y\sim 4-3x$ 3. Находим производная внешней $\left(e^y\right)'=...$ 4. производная внутренней $\left(4-3x\right)'$. 5. В производной внешней возвращаем замену и умножаем на производную внутренней.
Штрихование в одну строку: $\left(e^{4-3x}\right)'=e^{4-3x} \cdot \left(4-3x\right)'=e^{4-3x} \cdot (-3)=-3 e^{4-3x}$
Таблица Формулы дифференцирования сложных: правила замены ...
$\left(f\left(y\left(x\right)\right)\right)'=f_y'\cdot y_x'$ Метод Замены: $\left(f\left(y\left(x\right)\right)\right)'=\left(f\left(y\right)\right)'=f_y'\left(y\right)\cdot (y)'$.
$\left(y^n\right)'=n\cdot y^{n-1}\cdot (y)'$ $\left(\sqrt[3]{y}\right)'=\left(y^{\frac{1}{3}}\right)'=\frac{1}{3}\cdot y^{-\frac{2}{3}}\cdot (y)'$
$\left(\sin y\right)'=\cos y\cdot (y)'$ $\left(\cos y\right)'=-\sin y\cdot (y)'$
$\left(e^y\right)'=e^y\cdot (y)'$ $\left(a^y\right)'=a^y\cdot \ln a\cdot y'$
$\left(\ln y\right)'=\frac{1}{y}\cdot (y)'$ $\left(\log _ay\right)'=\left(\frac{\ln y}{\ln a}\right)'=\frac{1}{y\cdot \ln a}\cdot (y)'$
Задача 5: Найти производную "сложной" функций $\sqrt{5x^2-6}$
- $\left(\sqrt{5x^2-6}\right)'=$
- $y\sim 5x^2-6$ замена внутренней
- $\left(\sqrt{y}\right)'=\left(y^{\frac{1}{2}}\right)'=\frac{1}{2}\left(y\right)^{-\frac{1}{2}}\cdot \left(y\right)'$ (внешняя)'
- $\left(\sqrt{5x^2-6}\right)'=\left(\left(5x^2-6\right)^{\frac{1}{2}}\right)'=\frac{1}{2}\left(5x^2-6\right)^{-\frac{1}{2}}\cdot \left(5x^2-6\right)'=$ формула сложности
- $\left(5x^2-6\right)'=\left(5x^2\right)'-6'=10x$ (внутренняя)'
- $\left(\sqrt{5x^2-6}\right)'=\frac{1}{2}\left(5x^2-6\right)^{-\frac{1}{2}}\cdot 10x=\frac{5x}{\sqrt{5x^2-6}}$ (сложная)'
Комментарии: 1. Распознаем что есть что: $\sqrt{y}$ - внешняя, ... $5x^2-6$ - внутренняя. 2. Значит, правило замены: $y\sim 5x^2-6$ 3. Находим производную внешней функции $\left(\sqrt{y}\right)'$ 4. Находим производную внутренней функции $\left(5x^2-6\right)'$. 5. В формуле сложности умножаем оба производных, возвращая замену. 6. Окончательно: упрощаем полученные произведения.
Штрих в 1 строку: $\left(\sqrt{5x^2-6}\right)'=\left(\left(5x^2-6\right)^{\frac{1}{2}}\right)'=\frac{1}{2}\left(5x^2-6\right)^{-\frac{1}{2}}\cdot \left(5x^2-6\right)'=\frac{1}{2}\left(5x^2-6\right)^{-\frac{1}{2}}\cdot 10x=\frac{5x}{\sqrt{5x^2-6}}$
Задача 6: Найти производную "сложной" функций $\log _3\left(7-4x+5x^2\right)$
- $\left(\log _3\left(7-4x+5x^2\right)\right)'=$
- $y\sim 7-4x+5x^2$ замена внутренней
- $\left(\log _3y\right)'=\frac{1}{y\cdot \ln 3}\cdot \left(y\right)'$ (внешняя)'
- $\left(\log _3\left(7-4x+5x^2\right)\right)'=\frac{1}{\left(7-4x+5x^2\right)\cdot \ln 3}\cdot \left(7-4x+5x^2\right)'=$ формула сложности
- $\left(7-4x+5x^2\right)'=\left(7\right)'+\left(-4x\right)'+\left(5x^2\right)'=-4+10x$ (внутренняя)'
- $\left(\log _3\left(7-4x+5x^2\right)\right)'=\frac{1}{\left(7-4x+5x^2\right)\cdot \ln 3}\cdot \left(-4+10x\right)=\frac{10x-4}{\left(7-4x+5x^2\right)\cdot \ln 3}$ (сложная)'
Комментарии: 1. Распознаем: $e^y$ - внешняя, ... $4-3x$ - внутренняя. 2. правило замены: $y\sim 4-3x$ 3. Находим производная внешней $\left(e^y\right)'=...$ 4. производная внутренней $\left(4-3x\right)'$. 5. В производной внешней возвращаем замену и умножаем на производную внутренней.
diff=()': $\left(\log _3\left(7-4x+5x^2\right)\right)'=\frac{1}{\left(7-4x+5x^2\right)\cdot \ln 3}\cdot \left(7-4x+5x^2\right)'=\frac{1}{\left(7-4x+5x^2\right)\cdot \ln 3}\cdot \left(-4+10x\right)=\frac{10x-4}{\left(7-4x+5x^2\right)\cdot \ln 3}$
Еще примеры, разное исполнение, оформление
Иллюстационный пример: Учет сложности под разными функциями ....
Задача 7: Под аргументом разных функций находится квадратичное $x^2-5x$ - внутренняя функция.
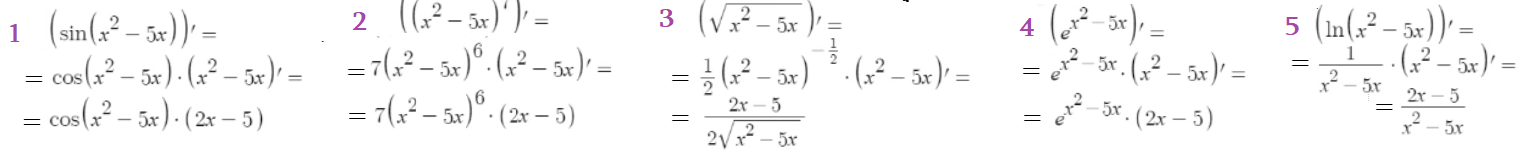
Задача 8: Еще примеры сложного диференцирования:
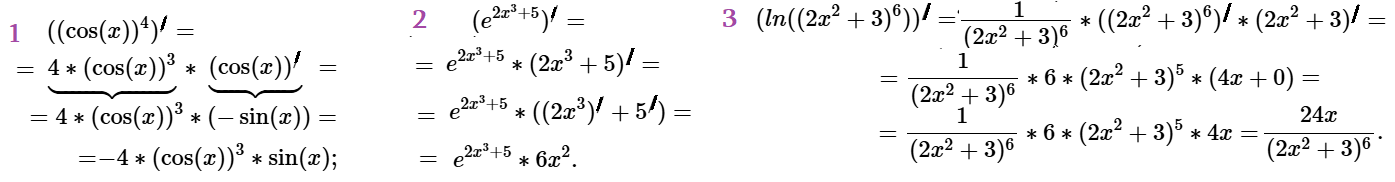
Комментарии: 1. 2. 3. 4. 5. 6. .
Комментарии: 1. 2. 3. 4. 5. 6. .
Упражнения (A):
Упражнения (В):
Упражнения (С):
Классная Интерактивная Доска:
