Алгоритм: Решение уравнений с ограничениями: .
-
Надо выписать ОДЗ - условия: условия существования выражений в уравнении. Решить получившиеся неравенства.
-
На тригонометрической окружности Е.Т.О. отметить области, промежутки точек, выполняющих условия ОДЗ.
-
Решить уравнение, отметить точки на Е.Т.О. , соответствующие полученным сериям решений.
-
Выбрать те точки, которые "попали" в допустимые промежутки, области. Какие числа-углы соответствуют этим точкам?
-
Написать серии для этих точек - эти серии и будут корнями нашего уравнения.
-
Выписать несколько конкретных корней. Перебрать разные $n$, $m$ целые числа, игнорируя заведомо не попадающие в ограничения.
-
Проверить каждый кандидат - корень: удовлетворяет ли условиям ограничения, входит ли в требуемый промежуток?
Задача 1: а) Решите уравнение $\left(\sin^2\frac{x}{2}+\frac{3\cdot \cos x}{2}\right)\left(\sqrt{3}\ctg x+1\right)\sqrt{-7\sin x}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $\left[-4\pi;-\frac{\pi}{2}\right]$ .
- ОДЗ: под радикалом $-7\sin x\ge0$ ; Условие на существование котангенса $x\ne\pi n$ - тоже самое, что $\sin x\ne0$;
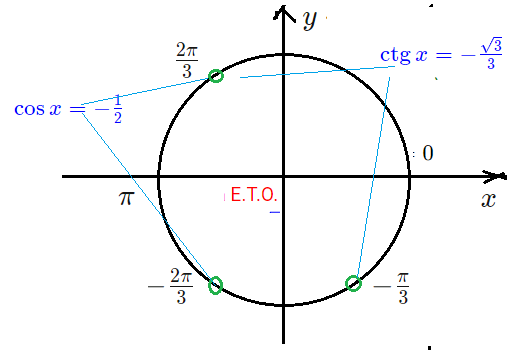
- Итоговое ОДЗ: $\sin x<0$ - корнями могуть быть углы из 3-ей и 4-ой четверти, в нижней части Е.Т.О окружности.
- Решаем уравнение: здесь произведение нескольких множителей равно 0. Значит, распад на случаи - каждый множитель = 0.
- Факт: "Произведение сравнить с нулем можно свести к сравнению с нулем каждого множителя":
- Уравнение: $A\cdot B\cdot C=0$ $\Rightarrow$ I случай $A=0$ , II случай $B=0$ , III случай $C=0$
- Последнее $\sqrt{-7\sin x}=0$ незачем решать т.к. мы уже установили при ОДЗ, что $\sin x\ne0$ из-за присутствия котангенса.
- I случай: $\sin^2\frac{x}{2}+\frac{3\cdot \cos x}{2}=0$ .
- Какие здесь углы? $\frac{x}{2}$ и $x$ . Значит, можем свести к одному углу!
- По формуле удвоенного угла $\cos x=1-2\sin^2\frac{x}{2}$ сможем прийти к замене $y=\sin\frac{x}{2}$. Но, решим по-другому ...
- по формуле понижения степени - половинного угла: $\frac{1-\cos x}{2}+\frac{3\cdot \cos x}{2}=0$ придем к простому
- $1+2\cos x=0$ $\Rightarrow$ $\cos x=-\frac{1}{2}$ его корни: $x=\frac{2\pi}{3}+2\pi n$ $x=-\frac{2\pi}{3}+2\pi m$
- Смотрим на Е.Т.О. - из этих двух точек-серий по ОДЗ нас устраивает только из 3-ей четверти: $x=-\frac{2\pi}{3}+2\pi m$
- II случай: $\sqrt{3}\ctg x+1=0$ "если в уравнении лишь одна функция, ее следует выразить ...":
- $\ctg x=-\frac{\sqrt{3}}{3}$ корни: 2 точки-серии $x=-\frac{\pi}{3}+\pi k$. Устраивает по ОДЗ: $x=-\frac{\pi}{3}+2\pi k$
- ответ a): $x=-\frac{2\pi}{3}+2\pi m$ $x=-\frac{\pi}{3}+2\pi k$ . (Две точки из нижней части Е.Т.О.).
Подробнее о проверке О.Д.З: Удобнее осуществить сразу же по простейщим уравнениям, по точкам Е.Т.О. до получения серий:
- Условие О.Д.З : $-7\sin x\ge0$ $\sin x\ne0$ существование радикалом котангенса
- 1-ое простейщее: $\cos x=-\frac{1}{2}$ выполняется в двух точках Е.Т.О. $T_{\frac{2\pi}{3}}$ и $T_{-\frac{2\pi}{3}}$ . В точке $T_{\frac{2\pi}{3}}$ из II четверти синус $>0$ $\to$ О.Д.З. не выполняется. В точке $T_{-\frac{2\pi}{3}}$ из III четверти синус $<0$ и косинус $\ne 0$ $\to$ О.Д.З. выполняется. Значит, серия $x=-\frac{2\pi}{3}+2\pi m$ удовлетворяют О.Д.З.
- 2-ое простейщее: $\ctg x=-\frac{\sqrt{3}}{3}$ $\to$ в двух точках Е.Т.О. $T_{\frac{2\pi}{3}}$ и $T_{-\frac{\pi}{3}}$ из II и IV четвертей. Точка $T_{\frac{2\pi}{3}}$ не годится ибо там синус $<0$. Точка $T_{-\frac{\pi}{3}}$ и всего его полные обороты удовлетворяют О.Д.З. $\to$ серия $x=-\frac{\pi}{3}+2\pi k$
Пункт б): Ищем корни из требуемого промежутка $\left[-4\pi;-\frac{\pi}{2}\right]$. Выпишем несколько возможных кандидатов для каждой серии:
- Из 1-ой серии: $-\frac{2\pi}{3}+2\pi$, $-\frac{2\pi}{3}$, $-\frac{2\pi}{3}-2\pi=-\frac{8\pi}{3}$, $-\frac{2\pi}{3}-4\pi$. Входит: 2-ой и 3-ий.
- Из 2-ой серии: $-\frac{\pi}{3}+2\pi$, $-\frac{\pi}{3}$, $-\frac{\pi}{3}-2\pi=-\frac{7\pi}{3}$, $-\frac{\pi}{3}-4\pi$. Попал лишь 3-ий.
- Требуемому ограничению удовлетворяют корни, ответ б): $-\frac{2\pi}{3}$, $-\frac{7\pi}{3}$, $-\frac{8\pi}{3}$,
Задача 2: а) Решите уравнение $\frac{3\cos^2 4x-7\left(\sin 4x+1\right)}{\sqrt{2\sin x-1}}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $\left[-4\pi;\frac{2\pi}{3}\right]$ .
- ОДЗ - условия: знаменатель не ноль, под радикалом неотрицательно: $2\sin x-1>0$
- Надо понять какие точки удовлетворяют ОДЗ на тригонометрической окружности Е.Т.О. Реши неравенство.
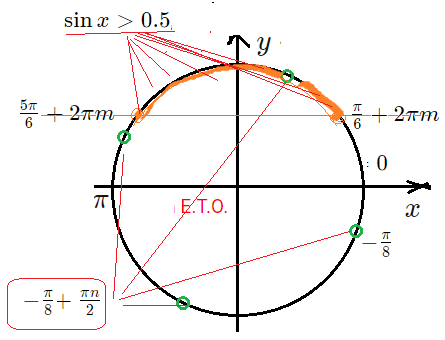
- Но пока уравнение: $2\sin x-1=0$ $\sin x=0.5$ $x=\frac{\pi}{6}+2\pi m$ $x=\frac{5\pi}{6}+2\pi m$
- Отметим эти точки-серии на Е.Т.О. Решение неравенства - это точки, в которых $\sin x>0.5$ , значит точки с $y$ - координатой выше $>0.5$ .
- Значит, неравенство и ОДЗ выполняется в точках дуги , верхней части окружности между точками $\frac{\pi}{6}$ и $\frac{5\pi}{6}$.
- Теперь решаем само уравнение: "Дробь = 0 $\Rightarrow$ числитель дроби = 0". Алгоритм: $\frac{A}{B}=0$ $\Rightarrow$ $A=0$
- Итак: $3\cos^24x-7\left(\sin4x+1\right)=0$ У нас 2 функции, 1 аргумент. Выразим первую через вторую:
- $3\cos^24x=1-\sin^24x$ - Основное тождество, $3\left(1-\sin^24x\right)-7\left(\sin4x+1\right)=0$ .
- Упростим: $3\sin^24x+7\sin4x+4=0$ 1 функция, 1 аргумент - все готово к методу замены:
- замена $y=\sin4x$ подстановка: $3y^2+7y+4=0$ корни: $y=-1$ $y=-\frac{4}{3}$
- $y=-1$ возвратное: $\sin4x=-1$ $\Rightarrow$ $4x=-\frac{\pi}{2}+2\pi n$ $\Rightarrow$ $x=-\frac{\pi}{8}+\frac{\pi n}{2}$
- $y=-\frac{4}{3}$ возвратное: $\sin4x=-\frac{4}{3}$ - нет решениий, т.к $-\frac{4}{3}<-1$ , а синус не может стать меньше $<-1$
- Отметим серию $x=-\frac{\pi}{8}+\frac{\pi n}{2}$ - это точки, получающиеся от точки $-\frac{\pi}{8}$ прокруткой четверть оборотов $\frac{\pi}{2}$.
- Получаются четыре точки на Е.Т.О.: $-\frac{\pi}{8}$, $\frac{3\pi}{8}$, $7\frac{\pi}{8}$, $-5\frac{\pi}{8}$.
- Из этих 4-х точек в интервале ОДЗ $\left(\frac{\pi}{6};\frac{5\pi}{6}\right)$ находится только точка $\frac{3\pi}{8}$ .
- ОДЗ удволетворяют углы: $\frac{3\pi}{8}$ и его $2\pi$ - прокуртки. ответ а): $\frac{3\pi}{8}+2\pi n$
- Пункт б): Ищем корни из требуемого промежутка . Выпишем несколько возможных кандидатов из серии $\frac{3\pi}{8}+2\pi n$:
- кандидаты: $\frac{19\pi}{8}$ $\frac{3\pi}{8}$ $-\frac{13\pi}{8}$ $-\frac{29\pi}{8}$ $-\frac{45\pi}{8}$ . Какие из них попадают в интервал $\left[-4\pi;\frac{2\pi}{3}\right]$
- Проверка принадлежности промежутку ограничения: ответ б): $\frac{3\pi}{8}$ $-\frac{13\pi}{8}$ $-\frac{29\pi}{8}$,
Послесловие: Какие навыки, умения, смыслы, понятия надо знать?
- Е.Т.О - связь углов, точек на окружности, серии углов, прокрутки в пол-оборота, полный оборот, части.
- Формулы решения простейших тригонометрических уравнений, интерпретация в виде точек на Е.Т.О.
- Решение неравенств, изображение решений на Е.Т.О. Перевод точек на серии углов и наоборот.
- Анализ ОДЗ: радикалы, знаменатели, тангенс-котангенс. Анализ условий ограничений. Интерпретация на Е.Т.О.
- Методы решения тригонометрических уравнений: простейших, метод замены, разложение на множители, понижение степени, однородные.
Интерактивная Доска
Упражнения
