I.     Тестирование по задачам ЕГЭ №1

Порешайте комбинированные задачи по темам ЕГЭ №1. Если обнаружились проблемы, то повторите основы планиметрии.

II - VI.     Теория: формулы, свойства, теоремы.

Ознакомьтесь с кратким изложением основных определений, свойств, формул и теорем планиметрии.

VII.     Упражнения для закрепления

Тренируйтесь по типам задач, проверяйте свои знания и навыки решения типовых задач

Рекоммендуемые интерактивные уроки   mathematicos по темам планиметрия

I.     Тестирование:     ЕГЭ задания №1,      планиметрия, задачи по-проще:

II.   Треугольники. Темы.   Краткая теория

• Углы.   Сумма углов. Внешний угол. Углы между медианой, биссектрисой, высотой.
• Теорема Пифагора. Прямоугольный треугольник. Равнобедренный треугольник. Равносторонный треугольник. Высота, медиана.
• Площадь треугольника. Площадь прямоугольного треугольника.
• Тригонометрия острых углов. Расчеты прямоугольного треугольника. Вычисления отрезков и сторон треугольника.
• Подобие. Коэффициент подобия. Отношение отрезков и площадей подобных треугольников. О высоте и медиане.
• Формула площади через синус. Теорема Синусов. Теорема Косинусов.

Сумма смежных углов = 180.     Вертикальные углы равны.          При трансверсальях:      сумма односторонних углов = 180,      накрест лежащие углы равны,    соответственные углы равны.

Сумма всех углов    треугольника = 180 градусов.    **Внешний угол треугольника равен сумме двух углов треугольника.      Сумма острых углов прямоугольного треугольника = 90 градусов.

Площадь   треугольника = половине * любая сторона * свою высоту.     Площадь прямоугольного треугольника   = катет * катет : 2.

Теорема Пифагора:    Квадрат гипотенузы = сумме квадратов катетов.     Равнобедренный   треугольник:: боковые стороны равны. Углы у основания равны. Из вершины высота, медиана, биссектриса совпадают.   Равносторонный   треугольник:: все стороны равны. Все углы 60 градусов.       Высота в любом треугольнике = удвоенная площадь деленная на свою сторону

Медиана к гипотенузе режет на два равнобедреных.     Медиана к гипотенузе:= половине гипотенузы.   Высота к гипотенузе делит на два подобных прямоугольных.    Катет напротив 30 град = половине гипотенузы.     Равнобедренный треугольник режется высотой на два равных прямоугольных.   Равносторонный треугольник режется высотой на два равных прямоугольных с 30 град.

Синус - отношение противолежащего катета к гипотенузе,      Косинус - отношение прилежащего катета к гипотенузе,    Тангенс - отношение противолежащего катета к прилежащему.    $\sin A=\frac{BC}{AB}$,       $\cos A=\frac{AC}{AB}$,        $\tg A=\frac{BC}{AC}$,    $\sin B=\cos A$,    $\cos B=\sin A$.

Катет = гипотенуза, умноженный на синус (или косинус).         Гипотенуза = катет, деленный на синус (или косинус).      Катет = другой катет, умноженный (деленный) на тангенс.

Формулы:,   $C=90$,     $BC=AB\cdot\sin A$, $AC=AB\cdot\cos A$,        Тождества:      $\sin^2\alpha+\cos^2\alpha=1$      ; Из синуса как найти косинус?     $\cos\alpha=\pm \sqrt{1-\sin^2\alpha}$ ;       $\tg\alpha=\frac{\sin\alpha}{\cos\alpha}$        ;     Тупые углы:      $\sin\left(\alpha\right)=\sin\left(180-\alpha\right)$                               $\cos\left(\alpha\right)=-\cos\left(180-\alpha\right)$ ,   $\tg\left(\alpha\right)=-\tg\left(180-\alpha\right)$

Прямоугольные:   "с $30^o$":    катет напротив = половине гипотенузы.    $a=\frac{c}{2}$    ;    $b=\frac{\sqrt{3}}{2}c$ .     "с $45^o$":   является равнобедренным, прямоугольным    ;   катеты через гипотенузу     $a=b=\frac{\sqrt{2}}{2}c$             Таблица:         $\sin 30=\frac{1}{2}$,       $\cos 30=\frac{\sqrt{3}}{2}$,       $\tg 30=\frac{\sqrt{3}}{3}$.            $\sin 60=\frac{\sqrt{3}}{2}$,       $\cos 60=\frac{1}{2}$,       $\tg 60=\sqrt{3}$,       $\sin 45=\frac{\sqrt{2}}{2}$,       $\cos 45=\frac{1}{2}$,       $\tg 45=1$.          $\sin 135=-\frac{\sqrt{2}}{2}$,       $\cos 135=\frac{1}{2}$,       $\tg 135=1$,         $\sin 120=\sin 60$,       $\cos 120=-\cos 60$,            $\sin 135=\sin 45$,       $\cos 135=-\cos 45$,         $\sin 150=\sin 30$,       $\cos 150=-\cos 30$,       $\sin 163=\sin 17$,       $\cos 163=-\cos 17$.

Подобие двух треугольников:    Состав углов одинаковый    $\angle A=\angle M$,     $\angle B=\angle K$,   $\angle C=\angle E$    $\Rightarrow $            $\bigtriangleup ABC\sim \bigtriangleup MKE$         $\frac{AC}{ME}=\frac{AB}{MK}=\frac{BC}{KE}$             $=k$ -   коэффициент подобия.     Признак I.   Равенство двух углов,    Признак II.   Пропорциональность двух сторон и равенство угла м/ж ними, Признак III.   Пропорциональность трёх сторон.

О важном:      какие составы углов? равные? какие стороны соответственные, схожие?   Коэффициент подобия = отношению соответственных сторон 1-го и 2-го треугольников.    Отношение всех соответствующих отрезков = $k$.       Квадрат   коэффициента = отношении площадей подобных.

О медианах: Три медианы треугольника пересекаются в одной точке, делятся этой точкой в пропорции 2 : 1,     треть и две третьих.

О высоте в прямоугольном:   делит на два подобных между собой и исходному.    Квадрат высоты = произведению отрезков гипотенузы.

Нахождение высоты треугольника:   Высота в любом треугольнике = удвоенная площадь деленная на свою сторону.

Теорема биссектрис:    делит сторону треугольника на два отрезка, пропорциональных другим двум сторонам треугольника.

О средней линии: параллелен стороне и = его половине,   отсекает подобный исходному треугольник,   2 : 1, площадь 4-раза меньше.

О линии, параллельной к стороне:   отсекает подобный исходному треугольник. Отношение их площадей = $k^2$.

Формула площади треугольника:       через синус:   $S=\frac{1}{2}\cdot a\cdot b\cdot\sin C$.             через высоту:   $S=\frac{1}{2}ah$.

Теорема Косинусов     $AB^2=AC^2+BC^2-2\cdot AC\cdot BC\cdot\cos ACB$     Квадрат любой стороны =   сумме квадратов двух других сторон     минус     удвоенное произведение сторон   на    косинус угла между ними.          

Теорема Синусов     $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$     Отношения сторон к синусу   своего   постоянны = $2R$.       -радиус описанной окружности.          ,

Пропорции т. синусов::           $\frac{a}{\sin A}=\frac{b}{\sin B}$                 $\frac{a}{\sin A}=\frac{c}{\sin C}$                   $\frac{b}{\sin B}=\frac{c}{\sin C}$.        Синус угла можем найти через площадь (о площади), либо через другой синус и стороны (т. синусов).      Нахождение высоты: площадь по одной формуле, неизвестную высотупо другой формуле площади.        Нахождение одно из 4-х (две стороны + два синуса противолежащих): через теорему синусов.    Нахождение одно из 4-х (три стороны + косинус угла):   через теорему косинусов.     Нахождение медианы: находим косинус угла по т. косинусов, медиану по теореме косинусов для своего треугольника.

III. Именные 4х-угольники: трапеция, параллелограмм, прямоугольник, ромб, квадрат    

Трапеция $\in$ четырехугольник с двумя параллельными сторонами (основания) ;         Параллелограмм   $\in$ трапеция, боковые стороно тоже параллельны ;       Прямоугольник    $\in$   параллелограмм с углами $90^o$ ;   Ромб    $\in$   параллелограмм с равными сторонами.   Квадрат    $\in$   ромб с углами $90^o$.

Расчет углов:     Сумма   углов 4-х-угольника = $360^o$. .      Используются свойства углов    Сумма смежных = $180^o$.     Вертикальные равные. .       Также, из-за параллельности сторон и секущей (стороны, диагонали) образуются     углы при трансверсалях: накрест лежащие равные;     соответственные равны;      сумма односторонних = $180^o$ ;

В равнобедренной трапеции диагонали одинаковые, образуют у оснований равнобедренные треугольники.   Важно: высоты   отсекают одинаковые прямоугольные треугольники, (углы, Пифагор, тригонометрия).   Высоты   делят основание на 3 части: средняя = основанию, по краям одинаковые =   полуразности оснований .

В прямоугольной трапеции   главное высота:. Отсекает прямоугольник и прямоугольный треугольник. Основание делит на = меньшему основанию = разности оснований. Пифагор, углы, тригонометрия.

Способы вычислений через формулы и свойства треугольников:   при высотах, при диагоналях могут образоваться разные расчетные треугольники (прямоугольные, равнобедренные, подобные) . Чтоб найти отрезок, его надо признать каким-то элементом какого-нибудь треугольника (высотой, медианой, катетом, гипотенузой, средней линией, ....).

Полезно искать прямоугольный треугольник и применять Теорему Пифагора: сумма квадратов катетов = квадрату гипотенузы.

Прямоугольный треугольник:   "с $30^o$":    катет = 0,5 гипотенузы. "с $45^o$":   является равнобедренным,    ;   катеты = $\frac{\sqrt{2}}{2}$ на гипотенузу               Тригонометрия:            $\cos 30=\frac{\sqrt{3}}{2}$,          $\cos 60=\frac{1}{2}$,       $\tg 60=\sqrt{3}$,           $\sin 45=\frac{\sqrt{2}}{2}$,       $\cos 45=\frac{1}{2}$,             $\sin 135=-\frac{\sqrt{2}}{2}$.            катет = sin (cos) * гипотенузу. гипотенуза = катет : sin (cos). катет = tg * катет

Увидеть подобные треугольники через равенства углов и воспользоватся пропорциями: отношения отрезков = $k$, отношения площадей = $k^2$

• Средняя линия трапеции делит боковые стороны, диагонали по серединам. Параллельна основаниям и = их полусумме.
• Биссектрисы в именных 4-х-угольниках отсекают равнобедренные треугольники (накрест-лежащие углы). Отрезки равны.
• Диагонали в именных 4-х-угольниках, кроме трапеции, делятся точкой пересечения по серединам, пополам.
• Диагонали трапеции образуют с основаниями подобные треугольники, $k$ = отношению оснований. Диагонали делятся $1:k$.
• Диагональ трапеции делит среднюю линию на отрезки - средние линии треугольников, равные половинам оснований.
• Диагонали ромба перпендикулярны, 90, и являются биссектрисами углов. Площадь = 0,5 произведения диагоналей.
• Диагональ ромба делит на 2 равнобедренных.    Диагонали ромба делят ромб на 4 одинаковых прямоугольных.
• Диагонали прямоугольника равные. (Пифагор, стороны).           Диагонали квадрата = $\sqrt \cdot $ сторона.
• Биссектрисы односторонных углов пересекаются перпендикулярно,$180^o$, образуют прямоугольный треугольник
• Любой 4-х-угольник:   Соединить середины сторон - получится параллелограмм.     См. средние линии, диагонали.

Аддитивность Площадей:     Площадь целой = сумме площадей кусков.           Площадь любой фигуры:    средняя ширина умноженная на высоту.      Средняя = (верхняя + нижняя) : 2.       Площади могут быть найдены путем складывания, вычитания кусков.

Площади:        Трапеции:     $s=\frac{a+b}{2}\cdot h$        параллелограмма:   $S=a\cdot h$,    $S= a\cdot b\cdot\sin C$.    ромба:   $S=a\cdot h$,       $S=a^2\cdot\sin A$,      диагонали    $S=\frac{d_1\cdot d_2}{2}$ .     прямоугольника:      $S= a\cdot b$.      квадрата:   $S=a^2$.     любого четырехугольника:    $S=\frac{1}{2}\cdot d_1\cdot d_2\cdot\sin \angle \left(d_1;d_2\right)$    ... треугольника $S=0,5\cdot a\cdot h$,    $S=0,5\cdot a\cdot b\cdot\sin C$, Heron.

Отношение площади:    Во сколько раз площадь одной фигуры больше, чем другой?   Какую долю площади занимает кусок в фигуре?     Если высоты равные, то через отношения нужных сторон ...      Если подобные, то через отношения площадей = $k^2$.    .... Медиана делит треугольник наа равновеликие ...

Нахождение высоты   через формулу площади фигуры. Конечно, предварительно найти площадь по другой формуле._

IV.    Окружности:    углы,    отрезки    

Вписанный угол = половине   центрального угла, опирающегося на ту же дугу. Внутренний Угол (м/ж хордами) =   полусумме дуг, отсеченных хордами.     Внешний угол   (м/жд двумя секщими из одной точки) =   полуразности дуг, заключенных секущими.   Угол между касательной и хордой   = половине дуги, заключенной м/ж ними.

Главное в окружности:      много углов, мало дуг. Углы связаны (определяются) с дугами.    Искать равные углы. Увидеть подобные треугольники.

Произведение отрезков пересекающихся   хорд     для каждой хорды одно и то же число, постоянное. произведение отрезков одной хорды   равен произведению отрезков другой хорды .

О произведении отрезков двух секущих:         Произведение    длин   отрезков   секущих   до    первой   и   второй   точек   пересечения с окружностью есть число постоянное.

О касательной и секущей из одной точки:       квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.

• Касательная и радиус в точке касания:    .... образуют   прямоугольный треугольник, 90°.
• Радиус,    проведенный в точке касания   касательной,    перпендикулярен касательной, 90°
• Две касательных из одной точки   равны, с радиусами образуют 2 равных прямоугольных треугольника.

V.   Вписанные и описанные окружности

• Геометрическое место точек, равноудаленных от обеих сторон угла   - это   биссектриса. (вписанная окружность)
• Геометрическое место точек, равноудаленных от обеих вершин отрезка   - это   срединный перпендикуляр. (описанная окружность)

Вписанная окружность в фигуру:       Центр находится на пересечении биссектрис и равноудален от сторон. Радиус   вписанной   окружности:        $r=\frac{S}{p}$       ,        $S=p\cdot r$.      $p$ - полупериметр:}   Радиус, проведенный к точкам касания сторон   перпендикулярен им.       Отрезки сторон - касательные до точек касания, проведенные из одной вершины    попарно   равны..

Описанная    окружность    вокруг   фигуры::    центр находится на пересечении серединных перпендикуляров   сторон и равноудален от вершин.         Описанная   окружность    вокруг   треугольника:   Формула радиуса   описанной:     $R=\frac{a\cdot b\cdot c}{4\cdot S}$ ;    $S=\frac{a\cdot b\cdot c}{4\cdot R}$ .        Теорема Синусов через радиус      $\frac{\sin\angle A}{a}=\frac{1}{2R}$ ;      $\frac{\sin\angle B}{b}=\frac{1}{2R}$ ;    $\frac{\sin\angle C}{c}=\frac{1}{2R}$

Теорема, Вписанная окружность в четырехугольник:   Попарные   суммы противоположных сторон четырехугольника равны    $AB+CD=BC+AD$    (из-за равных касательных).

Теорема, Описанная окружность вокруг четырехугольника:    Попарные суммы противоложных углов   четырехугольника    равны   180° :    $\angle A+\angle C=180=\angle B+\angle D$   

Правильный n - угольник:    Описанная    окружность    вокруг    n-угольника вершинами делится на n одинаковых дуг    каждый $\frac{360^o}{n}$.:}     Любой угол м/ж ... вычисляются через эти дуги.    Соединение центра с каждой вершиной: одинаковые сектора, центральные углы, дуги, равнобедренные треугольники.    Можно связать все со всеми!    

Сектор, дуга:     центральный угол = $\alpha$,    $\Rightarrow$       Площадь сектора = $\frac{\alpha}{360^o}$ * Площадь круга;      Длина дуги = $\frac{\alpha}{360^o}$ * длина окружности.

Аддитивность Площадей:     Площадь целой = сумме площадей кусков.           Площадь любой фигуры:    средняя ширина умноженная на высоту.      Средняя = (верхняя + нижняя) : 2.       Площади могут быть найдены путем складывания, вычитания кусков.

Упражнения:   задачи планиметрии, по-проще

Треугольники:

Четырехугольники:

Окружности:

VI. Вся планиметрия: теоремы, свойства, формулы на 4-х сценах

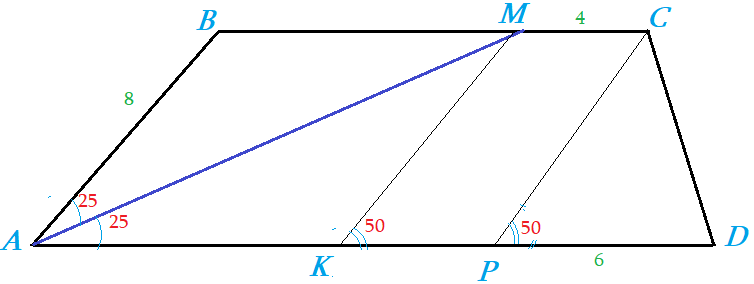
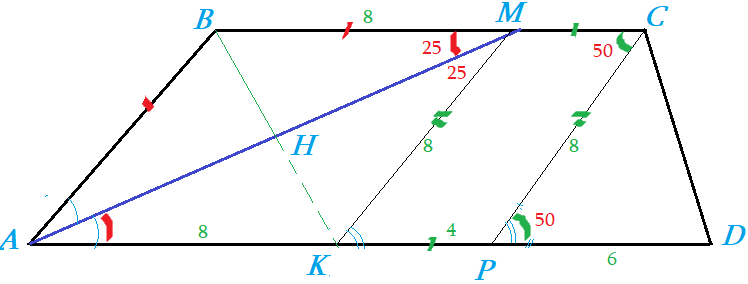
Сцена 1:    В трапеции $ABCD$   из вершины   $A$ проведена прямая   $AM$ составляющая со сторонами трапеции углы $25$ градусов. Из точки проведена $M$ прямая $MK$ к основанию под $50$ градусов. Из вершины $C$ проведенная прямая   $CP$ составляет также   $50$ градусов. Боковая сторона $AB$ равна 8, отрезок $KP$ равен 4, отрезок $PD$ равен $8$, .     Найти много чего!   

• Свойства: При пересечении двух параллельных линий с их Sекущей, образованные углы:
  
• Nакрест лежащие   углы равны                      $\angle MAD=\angle AMB$                 $\angle MCP=\angle CPD$              $\angle MKC=\angle KCP$
• Sумма Odносторонних   углов 180 град                        $\angle BAK+\angle ABC=180^o$                  $\angle KMC+\angle MCP=180^o$
• Sоответственные   углы равны                                $\angle MKP=\angle CPD$               $\angle BMK=\angle BCP$
  
•    Свойства: Uгол   =   Vершина   + два Lуча.                       .... противоположные Lучи, продолжения в обратную ... :
  
• Vертикальные   углы равны                      $\angle MAD=\angle AMB$                 $\angle MCP=\angle CPD$              $\angle MKC=\angle KCP$
• Sумма Sмежных   углов 180 град                        $\angle BAK+\angle ABC=180^o$                  $\angle KMC+\angle MCP=180^o$
•    Свойства:     Углы треугольника.    Биссектриса.      Равнобедренный треугольник:
• Bissектриса    из вершины угла делит его на два равных угла:         $\angle BAM=\angle MAK$           $\angle AKB=\angle BKM$
• Vнешний Uгол $\bigtriangleup -$ка равен сумме 2-х не Sмежных с ним.     $\angle AMC=\angle BAM+\angle ABM$               $\angle MPD=\angle PMK+\angle MKP$
• Sумма всех Uглов    треугольника равна 180 градусов.                  $\angle ABM+\angle BMA +\angle MAB=180^o$
• В Rавнобедренном Tреугольнике углы при Oсновании равны. Боковые Sтороны равны           $\angle BMA=\angle AMB$           $BA=MB$
• Sимметрии:     Ось Zеркальной sимметрии: слева и справа от Mедианы     $BH=h$   все одинаково!        $\bigtriangleup BHA=\bigtriangleup BHM$
• В Rавнобедренном: к Oснованию биссектриса, медиана и высота совпадают!    $\angle ABH=\angle HBM$      $AH=HM$      $BH \perp AM$

        

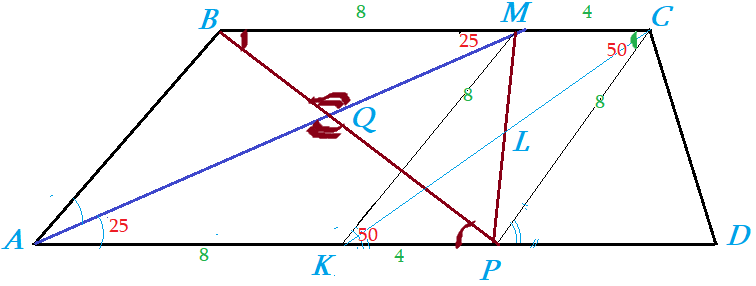
• Параллелограмм: $KMCP$      Противоположные    Sтороны   параллельны   и    равны    $KM=CP$    ,     $MC=KP$ .
• Противоположные     Uглы     $\angle KMC=\angle CPK$ ,        Сумма прилежащих Uглов $180^o$ :    $\angle KMC+\angle MKP=180$     ,     .
• Dиагонали образуют   равные   треугольники:       $\bigtriangleup MLC=\bigtriangleup KLP$      ;      $\bigtriangleup KLM=\bigtriangleup PLC$.
• Dиагонали параллелограмма делятся точкой пересечения пополам    $ML=LP=\frac{MP}{2}$      ,       $KL=LC=\frac{KC}{2}$ .
• Rомб: $ABMK$ Sимметричен относительно точки $H$ - пересечения диагоналей.      $H$ - центр Sимметрии.
• Симметричен относительно Dиагоналей.       Dиагональ - ось симметрии. .     Sтороны   равны     $AB=BM=MK=KA=a$
• Противолежащие Uглы    равны . Прилежащие в сумме 180.   Dиагонали делятся пополам .
• Dиагонали   взаимно перпендикулярны $AM \perp BK$   и   образуют равные Прямоугольные   $\bigtriangleup ABH = \bigtriangleup BHM$.
• Dиагонали    являются    Biссектрисами углов $\angle BAM=\angle MAK$ .   образуют Rавнобедренные   $\bigtriangleup$
• Tрапеция: $ABMP$ Параллельные   стороны   называются   Oснованиями,     $BM \parallel AP$ .   Другие две - боковыми сторонами.
• Сумма Oдносторонных Uглов при боковой стороне    $180^{\circ}$ :   $\angle BMP + \angle MPA = 180^{\circ}$    ,       $\angle ABM + \angle BAP = 180^{\circ}$.
• Dиагонали с основаниями   образуют равные   Nакрест лежащие углы:        $\angle MBP=\angle BPA$,         $\angle BMA=\angle MAP$
• Dиагонали с основаниями   образуют подобные треугольники           $\bigtriangleup BQM \sim \bigtriangleup AQP$            $\frac{BQM}{AQP}=(\frac{BM}{AQ})^2$

   

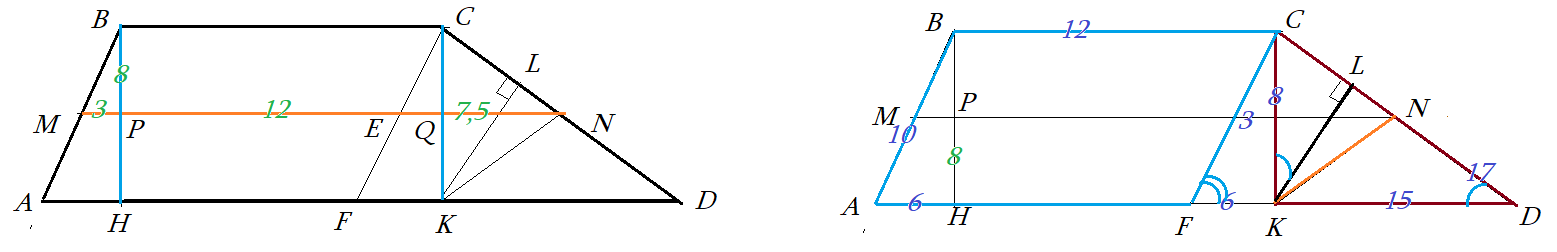
Сцена 2:    В трапеции $ABCD$   средняя линия   $MN$ разбывается высотами    $BH$ и $CK$   на три отрезка    $MP=3$,     $PQ=12$,     $QN=7,5$.    Высота трапеции равна   $BH=8$ . В треугольнике   $\bigtriangleup CKD$ проведены высота $KL$ и медиана $KN$. Из вершины $C$ проведена линия $CF$ параллельно боковой стороне $AB$.    Найти много чего!   

• Теорема Фалеса: Параллельные полоски отрезают от секущих пропорциональные отрезки     $\frac{BM}{AM}=\frac{BP}{PH}=\frac{CE}{EF}=\frac{CQ}{QK}=\frac{CN}{ND}$
• Средняя линия треугольника параллельна стороне и равна ее половине:          $QN=\frac{KD}{2}$    $MP=\frac{AH}{2}$      $EQ=\frac{FK}{2}$      $EN=\frac{FD}{2}$
• Средняя линия трапеции    параллельна основаниям и равна их полусумме:      $MN=\frac{BC+AD}{2}$     $MQ=\frac{BC+AD}{2}$       $PN=\frac{BC+HD}{2}$
• Площади фигур: Общее для всех: площадь равна произведению средней линии на высоту!         $S=\frac{a+b}{2} \cdot h$
• Площадь прямоугольника равна произведению длины на ширину    ... умножение сторон:          $S_{HBCK}=BC\cdot BH$
  
• Аддитивность площади:    площадь фигуры равен сумме площадей его частей, кусков.            $S_{ABCD}=S_{ABH}+S_{HBCK}+S_{KCD}$              $S_{HBK}=S_{HBCD}:2$         $S_{FCD}=S_{FCK}+S_{KCD}$            $S_{ABCF}=S_{ABH}+S_{HBCK}-S_{FCK}$
• Медиана на гипотенузу:    прямоугольного треугольника равна половине гипотенузы:         $KN=\frac{CD}{2}$        $HM=\frac{AB}{2}$
• Площадь прямоугольного треугольника равна половине произведения катетов:          $S_{KCD}=\frac{KD\cdot CK}{2}$        $S_{ABH}=\frac{AH\cdot BH}{2}$
• Площадь треугольника равен половине произведения стороны на свою высоту:        $S_{FCD}=\frac{FD\cdot CK}{2}$      $S_{KCD}=\frac{KL\cdot CK}{2}$
• Площадь параллелограмма равна произведению стороны на свою    высоту:           $S_{ABCF}=BC\cdot BH$

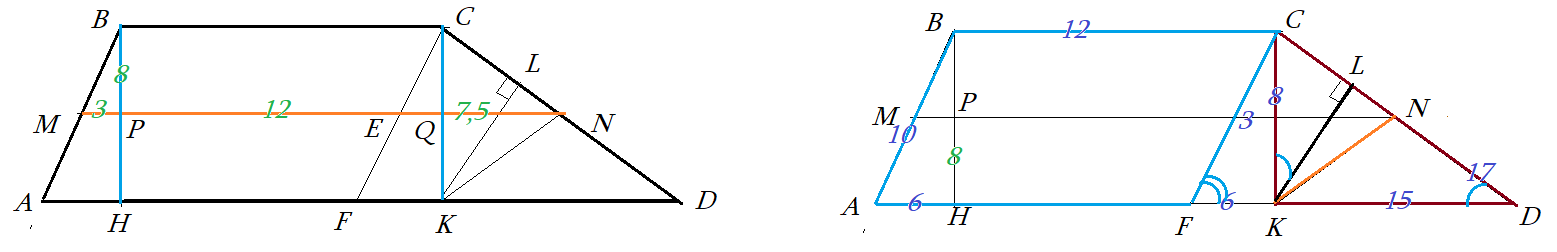
• Подобие прямоугольных треугольников ... хотя бы 1 острый одинаковый:        $\bigtriangleup KCD \sim \bigtriangleup KLD \sim \bigtriangleup KLC$       $\bigtriangleup BPM \sim \bigtriangleup BHA$.
• Тригонометрия углов прямоугольного треугольника: Все прямоугольные с одним и тем же   острым углом подобные!
• $\sin KCD=\frac{KD}{CD}$          $\sin KCD=\frac{KL}{KC}$          $\cos KCD=\frac{KC}{CD}$           $\tg KCD=\frac{KD}{CK}$         $\ctg KCD=\frac{CK}{KD}$          $\cos LKD=\frac{KL}{KD}$
• sin = противоположный : гипотенузу        cos = прилеж : гипотен        tg = протипол : прилеж         ctg = прилеж : протиполож
• Теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы.     $CK^2+KD^2=CD^2$             $KL^2+LN^2=KN^2$
• Основное тождество тригонометрии:        $\sin^2 \angle CDK+\cos^2 \angle CDK=1$              $\sin^2 \angle BAD+\cos^2 \angle BAD=1$
• Высота в прямоугольном делит на подобные, равен средне-геометрическому отрезков гипотенузы     $KL=\sqrt{CL\cdot LD}$
• Площадь треугольника равен половине произведения сторон на синус угла м/д    ними:        $S_{FCD}=\frac{1}{2} \cdot FD \cdot DC \cdot \sin\angle FDC$
• Площадь параллелограмма равна произведению стороны на синус угла м/д ними:           $S_{ABCF}=AB\cdot AF \cdot \sin\angle BAF$
• Теорема косинусов: Связь 3-х сторон и косинуса угла        $CD^2=FC^2+FD^2-2\cdot FC \cdot FD \cdot \cos \angle CFD$
• Тупой угол vs смежный с ним острый:          $\sin \angle CFA=+\sin \angle CFD$             $\cos \angle CFA=-\cos \angle CFD$

Сцена 3:    Дана окружность с центром $O$ и радиусом $r=R=7$. Точки     $A,B,C,D$   на окружности делят всю окружность пропорционально числам 5 : 3 : 2 : 2.   В этих точках проведены касательные к окружности. На рисунке образовались углы, треугольники вписанные и описанные, четыреъугольники вписанные т оптсанные. Найти много чего!   

• Пропорциональное деление    на доли 5 : 3 : 2 : 2 означает, что есть такое $x$, что полученные части равны     $5x$, $3x$, $2x$, $2x$
• Центральный угол угловую меру дуги, которую угол стягивает:                 $\angle AOD=∪AD$              $\angle AOB=∪AB$
• Вписанный угол равен половине угловой меры дуги, на которую угол опирается:       $ \angle BDA=\frac{\cup AB}{2}$             $\angle DAB=\frac{∪DC+∪CB}{2}$
• Радиусы образуют равнобедренные $\bigtriangleup$:    $OA=OB=R$     $OC=OD=R$    $\angle OCB=\angle OBC$
• Окружность описан вокруг 4-х угольника:     равные суммы противоположных углов          $\angle A+\angle B=\angle C+\angle D=180^{\circ}$
• Центр окружности, описанной вокруг    $n$-угольника:    находится на пересечении серединных перпендикуляров. Равноудален!
• Радиус окружности, описанной вокруг $\bigtriangleup ABD$:           $R\cdot 2S_{ABD}=AB\cdot BD\cdot DA$
• Связь радиуса описанной и стороны $\bigtriangleup ABC$:                 $\angle BAC=\frac{\angle BOC}{2}$         $\sin \angle BAC=\frac{0,5BC}{R}$
• Теорема Синусов,        $\bigtriangleup $:                $\frac{\sin \angle BAC}{BC}=\frac{\sin \angle CBA}{CA}=\frac{\sin \angle ACB}{AB}=\frac{1}{2R}$    синусы пропорциональны сторонам напротив.

                  

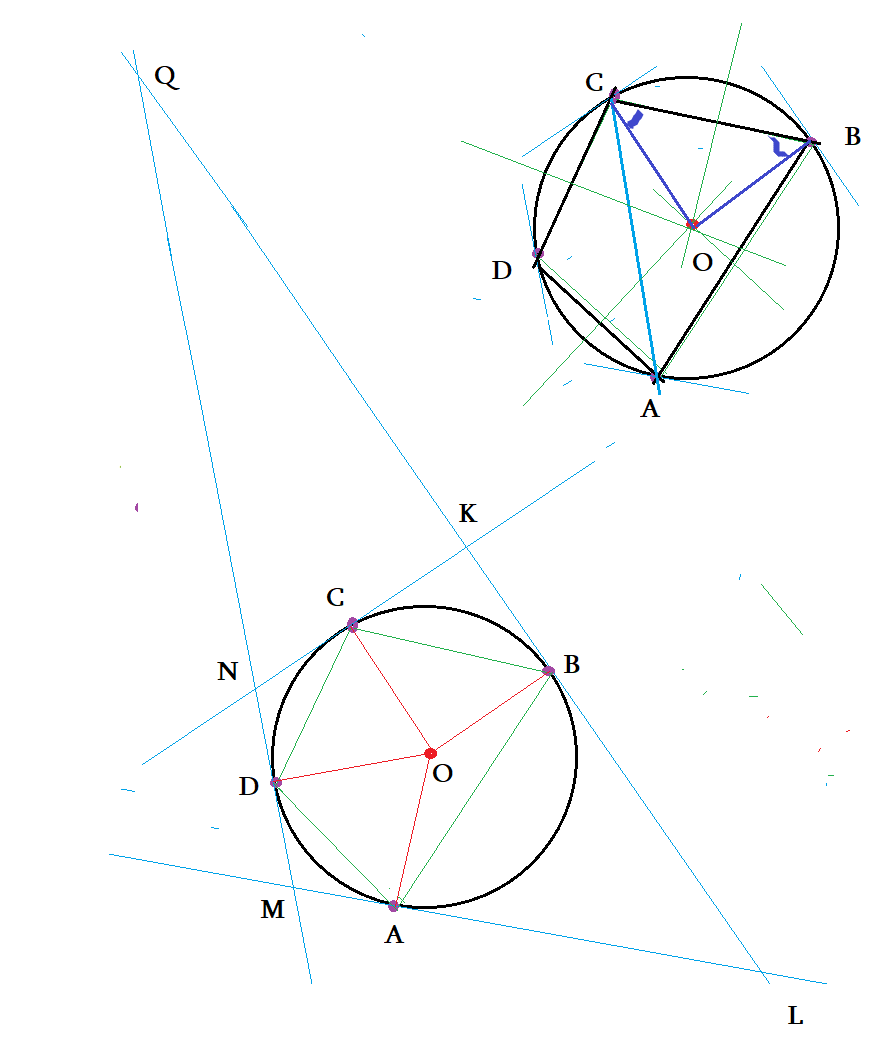
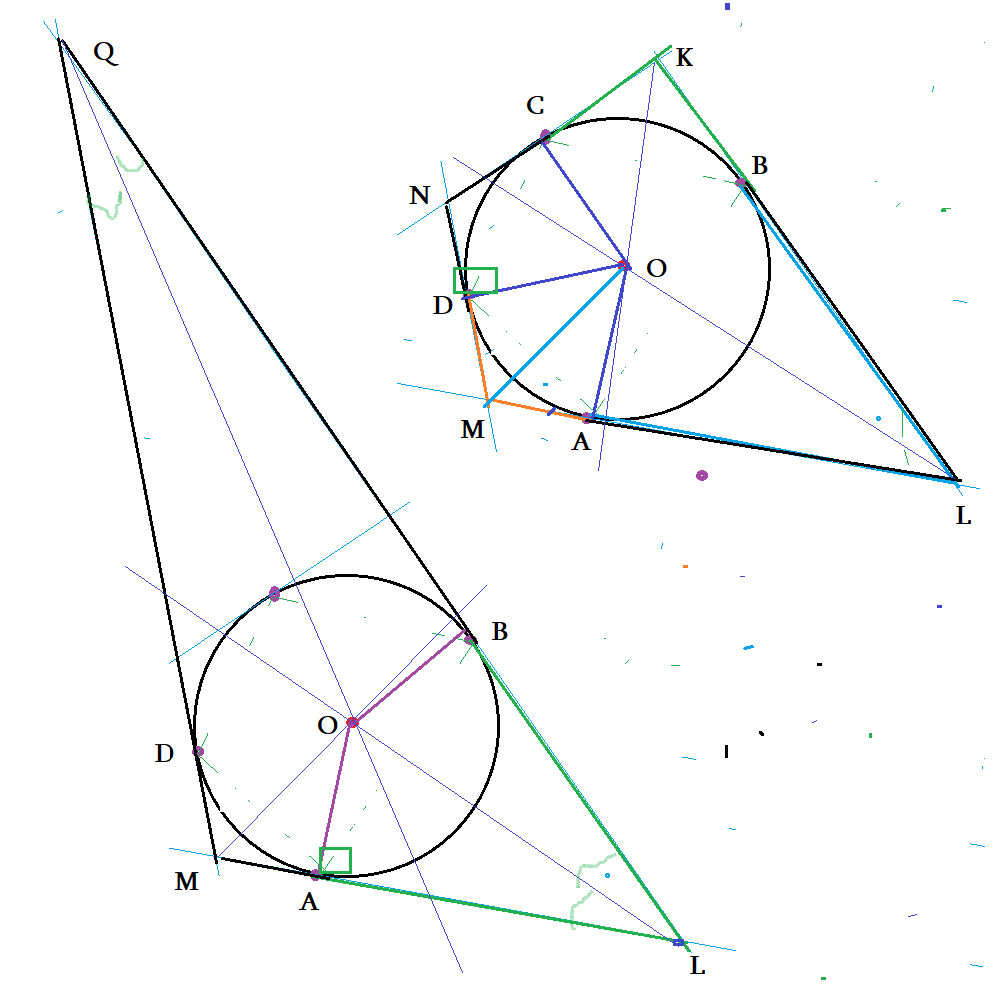
• Обе касательных от точки к окружности    равны:   $LA=LB$        $KC=KB$       $QD=QB$        $\bigtriangleup OMA=\bigtriangleup OMD$
• Касательная и радиус в точке касания    перпендикулярны:      $OA\perp ML$     $OC\perp NK$   $OB\perp QL$
• Центр вписанной окружности находится на пересечении биссектрис, равноудален от сторон.    $\angle MQO= \angle LMO$
• Радиус вписанной окружности в   $n$-угольник            $r\cdot p_{QML}=S_{QML}$        $r\cdot p_{MNKL}=S_{MNKL}$   полупериметр, площадь
• Окружность вписана в 4-х угольник:       равные суммы противоположных сторон:   $ML+NK=MN+KL$
• Соединение центра с вершинами и точками касания образует несколько пар равных прямоугольних $\bigtriangleup $
• Подобные $\bigtriangleup $-ов:         $\bigtriangleup QKN \sim \bigtriangleup QML $,    одинаковый состав углов, $\frac{QK}{QM}=\frac{QN}{QL}=\frac{KN}{ML}$.     $\angle QNK = \angle QLM $

Сцена 4:     В трапеции    $ABCD$ основание   $BC$ и боковая сторона    $CD$ являются касательными к окружности, описанной вокруг треугольника   $ABD$. Найдите площадь треугольника $ABD$, если известно, что     $AD=4\sqrt{3}$ и    $\angle BCD=120^{\circ}$. Боковые стороны продлены до пересечения. Докажите подобия, свойства секущих, хорд, углов.

• Касательные от точки к окружности равны    $CB=CD$   и перпендикулярны радиусам   $CB\perp OB$ ,   $CD\perp OD$
• Угол м\д касательной и хордой равен половине заключенной дуги    $ \angle CBD=\frac{\cup BD}{2}= \angle CDB$
• Одинаковый состав углов приводит к подобию     $\bigtriangleup BCD \sim \bigtriangleup ABD $      $\frac{BD}{AD}=\frac{BC}{AB}$
• Параллельные линии на окружности вырезают равные дуги:              $BC \parallel AB$           $\cup AB=\cup BD$
• Продолжение боковых сторон трапеции образует подобные треугольники         $\bigtriangleup AKD \sim \bigtriangleup BKC $
• Параллельная стороне треугольника отсекает подобный ему $\bigtriangleup $ :           $\frac{AK}{BK}=\frac{DK}{CK}=\frac{AD}{BC}=k$ - коэффициент подобия
• Отношения При Подобиях:        схожие отрезки относятся как   $k:1$;           площади как   $k^2:1$;        схожие   углы $1:1$

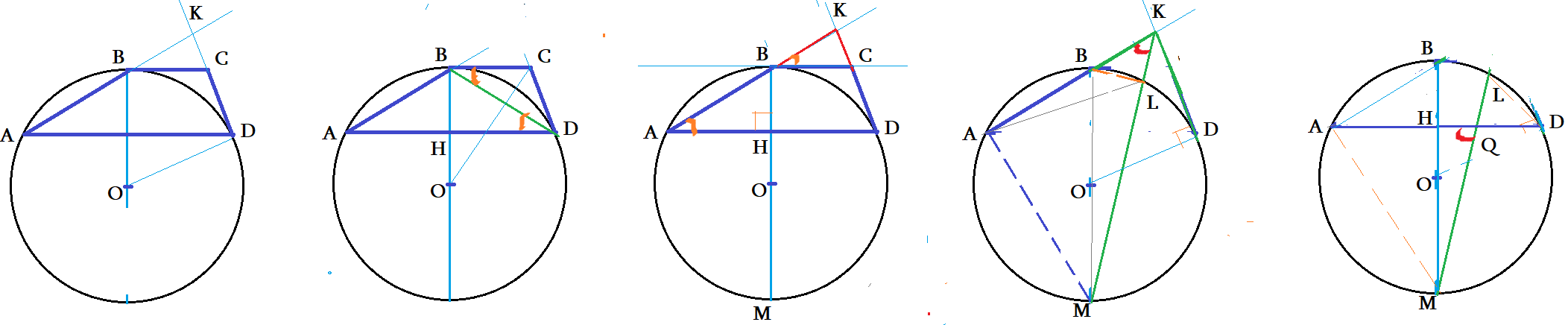
• Две секущих из внешней точки окружности образуют подобные треугольники         $\bigtriangleup KMB \sim \bigtriangleup KAL $
• Внешний угол окружности м\д секущими равен полуразности заключенных дуг     $ \angle AKM=\frac{\cup AM - \cup BL}{2}$
• Произведения отрезков секущих от одной точки равны м\д собой        $KB\cdot KA=KL\cdot KM$
• Квадрат касатальной равен произведению отрезков секущей из то же точки       $KD^2=KB\cdot KA$
• Две пересекающиеся хорды    образуют подобные треугольники           $\bigtriangleup QLD \sim \bigtriangleup QAM $
• Внутренний угол окружности м\д хордами равен полусумме заключенных дуг              $ \angle AQM=\frac{\cup AM - \cup LD}{2}$
• Произведения отрезков пересекающихся хорд    равны м\д собой           $LQ\cdot QM=DQ\cdot QA$ ,           $BH\cdot HM=AH\cdot HD$