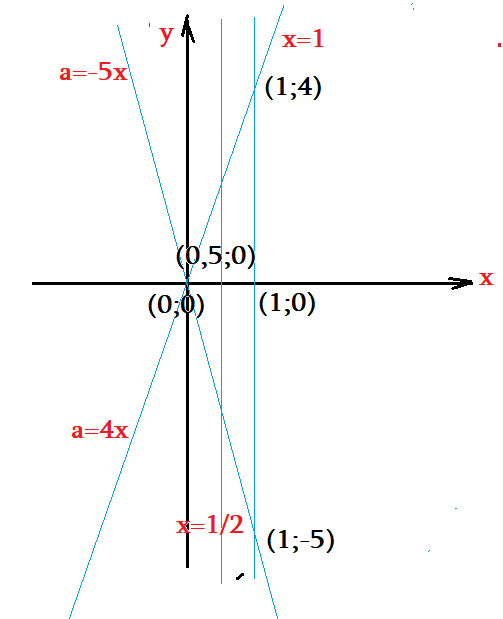
Задача:         Найти значения параметра   $a$, при котором уравнение          $\sqrt{2x-1}\ln\left(4x-a\right)=\sqrt{2x-1}\ln\left(5x+a\right)$     имеет более одного решения на отрезке       $\left[0;1\right]$

• ОДЗ:         $2x-1\ge0$     $4x-a>0$           $5x+a>0$         допустимость радикала и 2-х логарифмов.
• Какие   $x$    значения допустимы? И, главное, при каких парматерах $a$.
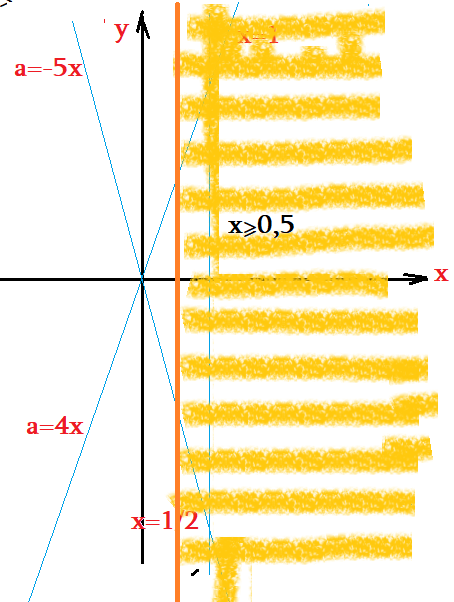
• Первое условие     $2x-1\ge0$    легко "осознать",   все числа   $x\ge 0,5$, т.е. правее   $0,5$.
• А аргументы логарифмов зависят от параметра $a$. Это значит: при разных параметрах получатся разные интервалы для   $x$.
• Как "визуализировать" области допустимости при различных параметрах ... чтобы "видеть" какие   $x$ допустимы при каких   $a$.
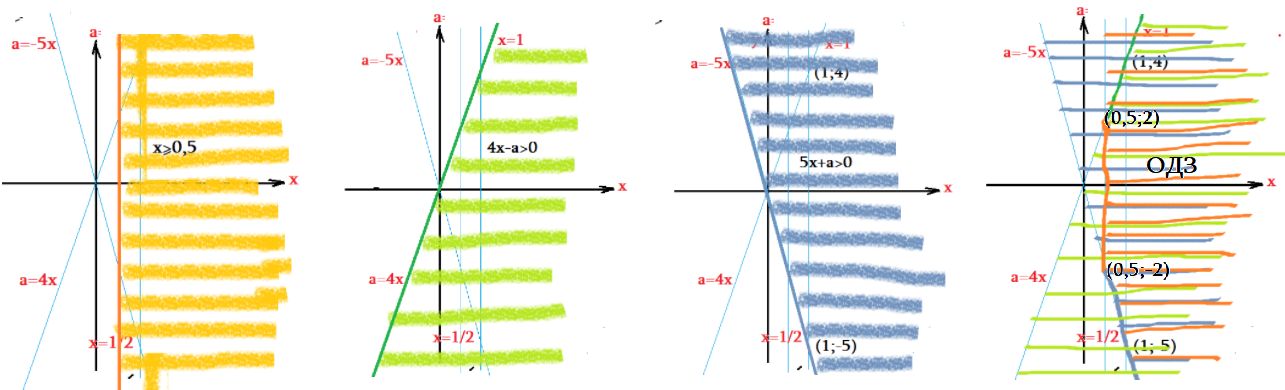
• "Нарисуем" решения неравенств      на координатной плоскости   $(x;a)$    и отметим области допустимости:
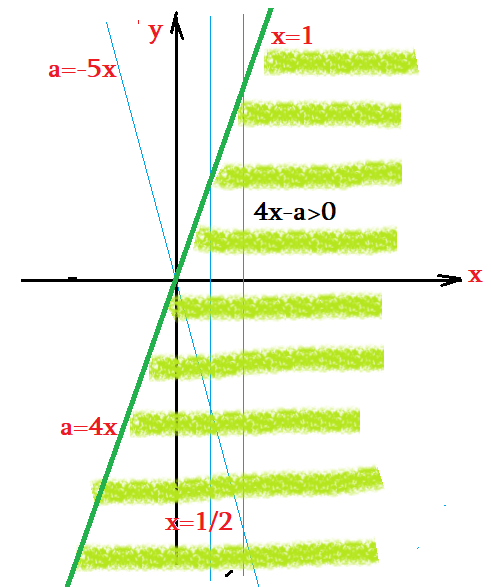
• Неравенство    $4x-a>0$ :   Критическая линия проходит по прямой   $4x-a=0$    $\Rightarrow$     $a=4x$. Нарисуем ее.
• Прямая   $a=4x$   делит плоскость    $(x;a)$ на две области: в левой неравенство не выполняется, в правой выполняется. Проверить!
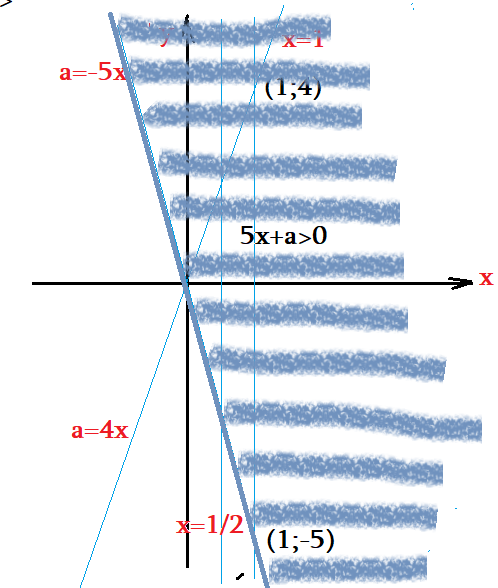
• $5x+a>0$ - критическая линия, "граница областей":   $a=-5x$ . установим область допустимости через контрольные точки. Правее...
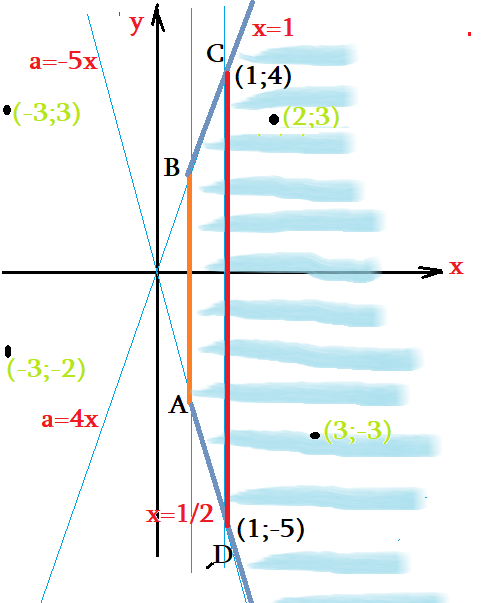
• ОДЗ должно состоять из общих точек всех полученных областей.     Пересечение областей    приведет к рисунку ....
• получились куски: где что выполняется --- на каких полуплоскостях - проверка подстановкой контрольных точек
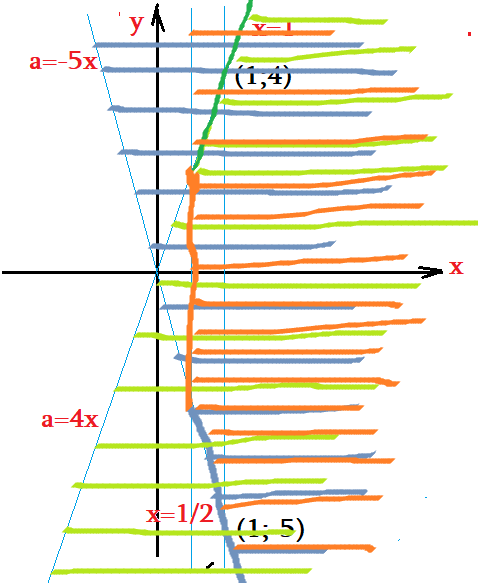
• Видим все точки, в которых выполняется ОДЗ - трапециовидная область правее $x=0,5$ и между лучами    $a=-5x$    и   $a=4x$

Решаем собственно уравнение   $\sqrt{2x-1}\ln\left(4x-a\right)=\sqrt{2x-1}\ln\left(5x+a\right)$   $\Rightarrow$    $\sqrt{2x-1}\left(\ln\left(4x-a\right)-\ln\left(5x+a\right)\right)=0$

• Сравнение произведения с нулем сводится к сравнению каждого множителя с нулем.
• $\sqrt{2x-1}$   дает решение $x=0,5$.   Но по "фотографии" ОДЗ видим, что оно корень только для $-2\le a\le2$. Точки отрезка $AB$.
• Другой множитель         $\ln\left(4x-a\right)-\ln\left(5x+a\right)=0$       $\Rightarrow$        $\ln\left(4x-a\right)=\ln\left(5x+a\right)$
• Сравнение логарифмов с одинаковыми основаниями сводится к сравнению аргументов:     $4x-a=5x+a$,    решение   $x=-2a$.
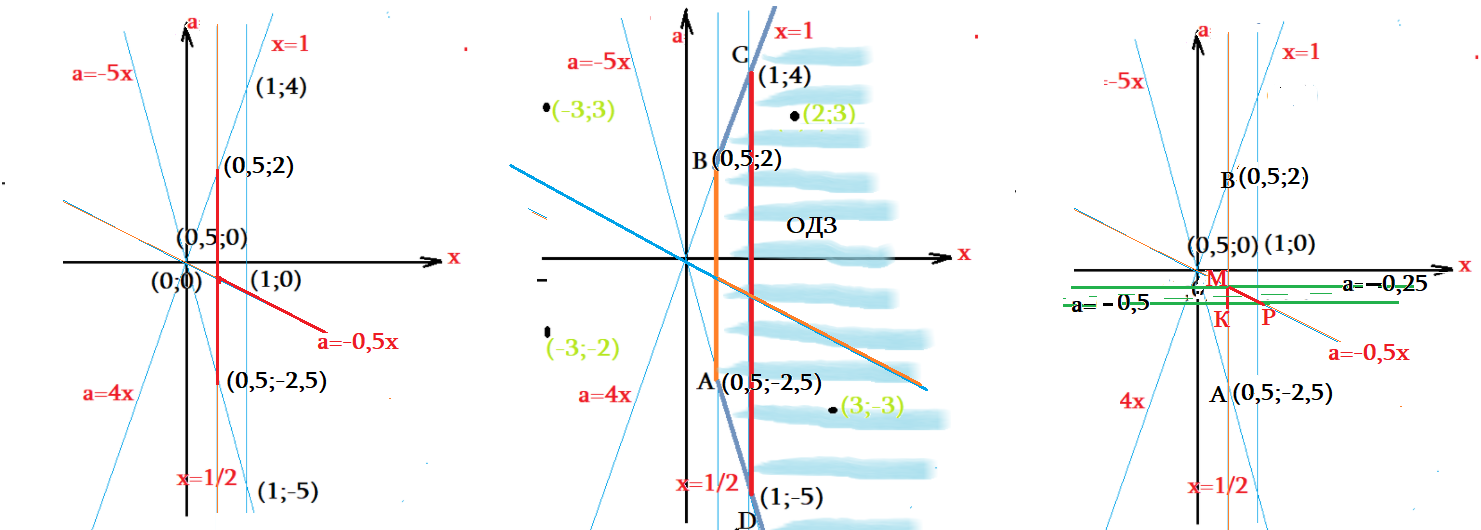
• "Нарисуем" решения $x=-2a$ -   прямую, точки которой удовлетворяют это равенство. Эта прямая   $a=-0,5x$
• Этот корень действителен только на той части прямой   $a=-0,5x$ , которая попадает на заштрихованной области ОДЗ ... луч вправо!
• Корень   $a=-0,5x$ с учетом ОДЗ дает точки на луче от $M$   вправо, включая точку $P$ и далее.
• Вычислим координаты всех особенных точек, пересечения прямых:   $A$ суть пересечение $a=-5x$ с $x=0,5$, т.е. $A(0,5;-2,5)$
• Точка $M$ пересечение прямых   $a=-0,5x$    и    $x=0,5$. Его координаты        $M(0,5;-0,25)$
• Точка $P$ дается пересечением прямых    $a=-0,5x$    и    $x=1$.   Его координаты        $P(1;-0,5)$
• Точка $K$ на уровне $P$, т.е.   $a=-0,5$, его координаты    $K(0,5;-0,5)$.

• В каких областях, кусках выполняются условия ОДЗ: проверим по контрольным точкам      $(2;3)$      $(3;-3)$     $(-3;3)$   $(-2;-3)$.
• Уточним область ОДЗ: все точки   $(x;a)$, находящиеся правее отрезка   $AB$ между лучами $BC$ и $AD$, включая все точки из   $AB$.
• Корнями являются точки отрезка $AB$   и луча $MP$:   все такие точки удовлетворяют уравнение и принадлежат ОДЗ.
• Последний штрих:   Какие корни попадyт в промежуток      $[0;1]$    и при каких параметрах получается более одного корня?
• Визуализация всех решений: проследим, на каких уровнях параметра появляются два корня, "подвигаем" горизонтальную линию ...
• Вспомним: нам нужны корни из промежутка    $[0;1]$, т.е. корни из полоски между вертикальными прямыми   $x=0$ и $x=1$.
• Посмотрим треугольник $MKP$ ....   только там горизонтальная линия пересечет решения два раза:   от уровня $M$   до уровня   $K$.
• Два корня, притом оба из промежутка $[0;1]$, появляются лишь между зелеными горизонтальными уровнями
• Более одного корня появляется от уровня       $a=-0,25$      до уровня     $a=-0,5$ . При этом исключая первое, там $1$ корень.
• Ответ:   при значениях   параметра    $a$     из полуинтервала      $[-2;-1)$       у исходного уравнения два корня из отрезка $[0;1]$.
• Проверка:   при   $a=-0,4$   корни:      $x=0,5$    и   $x=-0,8$.       Прямая    $a=-0,4$    два раза пересекает "фото" корней.
• при $a=-0,5$ корень по линии   $a=-0,5x$ дает крайнее значение $x=1$, т.е. выходит на границу промежутка   $[0;1]$.
  

Стратегия решения параметрических уравнений методом визуализации решений на графике $(x;a)$

1. Каждое условие ОДЗ "нарисовать" в виде области на координатной плоскости $(x;a)$:     Из условия ОДЗ выразить   $a$   через $x$ или наоборот    ....   Нарисовать граничную кривую ... в полученных кусках-областях учинить проверку контрольными точками ... отметить области выполнения ОДЗ.

2. Найти пересечение всех отдельных областей каждого условия ОДЗ. Полученная заштрихованная область - это те точки, пары $(x;a)$, удовлетворяющие всем требуемым условиям ОДЗ.
   

3. Решить уравнение без учета ОДЗ, нарисовать корни в виде кривых - зависимостей корней $x$ от параметра $a$.

4. Среди точек корней выделить те, которые находятся в заштрихованной ОДЗ области.        Куски, попадающие в ОДЗ.

5. Визуализация закончена:   мы видим воочию все корни, в том числе те, которые забракованы условиями ОДЗ. Мы видим корни, попадающиеся в требуемый промежуток. Мы можем, двигая горизонтальную линию   $a=const$ увидеть сколько и какие корни получаются при том или ином значении параметра $a$.

Задачи для самостоятельного решения:

№ 1:     Найдите значения параметра   $a$, при которых уравнение            $\sqrt{x+2a}\ln\left(x-a\right)=\left(x-1\right)\ln\left(x-a\right)$         имеет одно решения на отрезке       $\left[0;1\right]$

№ 2:      При каких значениях параметра уравнение          $\log _{x+1}\left(a+x-6\right)=2$     имеет хотя бы один корень       $-1<x\le 3$

№ 3:        Найдите все значения параметра    $a$   при которых уравнение $\left(a+3-\left|x-4\right|\right)\left(x^2-8x+10-a\right)=0$      имеет ровно   $2$   корня.

№ 4:      Найти все значения параметра $a$, при каждом из которых неравенство        $\left(x^2+a^2-13\right)\sqrt{2a+3x}\le0$         имеет не более двух решений.

№ 5:     Найдите все значения параметра $a$   при которых неравенство $\frac{x-2a-4}{x+3a-2}\le0$    выполняется при всех $x$    из промежутка     $1\le x\le3$

№ 6:     При каких значениях параметра система из двух неравенств     $\frac{x-ax-a}{x-2+2a}\ge 0$     и     $x-8>ax$     не имеет решений

№ 7:     Найдите все положительные значения a, при каждом из которых множеством решений неравенства   $\frac{x-2}{ax^2-\left(a^2+1\right)x+a}\le0$     является некоторый луч

Интерактивные Задачи: