Подробнее на эти темы, смотрите теорию:
- Урок здесь, XI . §18. minimum, maximum. Нахождение экстремумов функций.
- Урок здесь, XI . §19. Наибольшее и наименьшее значение функции на отрезке
min, max аналитически: условия экстремумов
Рассуждения о экстремальном: поведение функции (возрастание, убывание) в точке $x_0$ зависит от знака производной в точке $x_0$.
Функция возрастает ⇒ производная от функции положительна;__Функция убывает ⇒ производная от функции отрицательна; Функция принимает максимальное или минимальное значение в точке ⇒ производная от функции равна нулю;
- если $f'\left(x_0\right) > 0$ то $f\left(x_0-0,01\right) < f\left(x_0\right) < f\left(x_0+0,01\right)$ $\Rightarrow $ функция ⇑, возрастает.
- если $f'\left(x_0\right) < 0$ то $f\left(x_0-0,01\right) > f\left(x_0\right) > f\left(x_0+0,01\right)$ $\Rightarrow $ функция ⇓, убывает.
- если $f'\left(x_0\right)=0$ то ситуации более запутанные:
- $f\left(x_0-0,01\right) < f\left(x_0\right)$ и $f\left(x_0\right) > f\left(x_0+0,01\right)$ $\Leftrightarrow$ $x=x_0$ - максимума, в нем функция выше.
- В случае $f\left(x_0-0,01\right) > f\left(x_0\right)$ $f\left(x_0\right) < f\left(x_0+0,01\right)$, $x=x_0$ - точка минимума, нижайщее.
- Если ни то, ни другое, то точка перегиба: ... растет, прекращает рост ($f'=0$), опять растет ...
Определение: Точка, в которой производная обнуляется, называется экстремумом (min, max, перегиб).
- В этой точке наклон графика равен нулю, т.е. касательная к графику горизонтальна.
- Точка максимума - слева направо; функция растет ⇑, "застывает" в $x_0$" , затем убывает ⇓.
- max: слева - ( $x< x_0$, $f'>0$, $f$ ⇑); в точке - ($x=x_0$ притормаживает, $f'=0$); справа - ($x>x_0$, $f'<0$, $f$ ⇓).
- Точка минимума - слева направо; функция убывает ⇓, "застывает" в $x_0$" , затем растет ⇑.
- min: слева - ( $x< x_0$, $f'<0$, $f$ ⇓); в точке - ($x=x_0$ притормаживает, $f'=0$); справа - ($x>x_0$, f'>0$, $f$ ⇑).
- Экстремумы - это точки минимума и максимума функции, «вершины» и «впадины» на графике функции. Или перегиб.
Уравнение экстремумов: $f'\left(x\right)=0$ - в его корнях экстремумы, производная обнуляется.
Как определить: точка экстремума - это min, max или перегиб? Есть три способа:
- по поведению переходов "рост / убывание" исходной функции слева-справа от точки экстремума;
- либо поведение "отрицательности / положительности" производной чуть левее, чуть правее; Около точки!
- либо знак второй производной в этой точке (по смыслу это ускорение, кривизна):
- если 2-ая производная ("производная от производной") в точке $x_0$ положительна, то это точка минимума.
- если 2-ая производная в точке $x_0$ отрицательна, то это точка максимума. Касательная над графиком ...
- если же 2-ая производная в точке $x_0$ равна нулю, то -перегиб. Касательная пересекает график ...
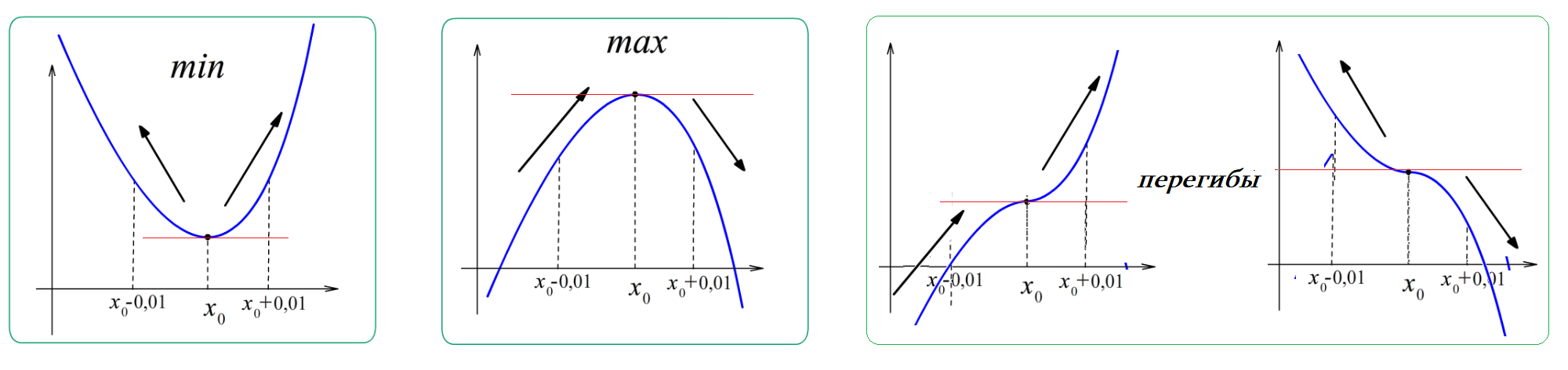
min: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) > f\left(x_0\right) < f\left(x_0+0,01\right)$ , $f'\left(x_0-0.01\right) < 0$ , $f'\left(x_0+0.01\right) > 0$ ; $f''\left(x_0\right) > 0$.
max: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) < f\left(x_0\right) > f\left(x_0+0,01\right)$ , $f'\left(x_0-0.01\right) > 0$ , $f'\left(x_0+0.01\right) < 0$ ; $f''\left(x_0\right) < 0$.
перегиб: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) < f\left(x_0\right) < f\left(x_0+0,01\right)$ $f'\left(x_0-0.01\right) < 0$ , $f'\left(x_0+0.01\right) < 0$ ; $f''\left(x_0\right) = 0$.
Задача 1: Найти точки минимума и максимума функции $f\left(x\right)=x^3-3x+2$
- $f\left(x\right)=x^3-3x+2$ функция
- $\left(x^3-3x+2\right)'=3x^2-3$ производная $f'\left(x\right)$ от нашей функции
- $3x^2-3=0$ $x=1$ $x=-1$ уравнение экстремума $f'\left(x\right)=0$, решение
- $X_f$ $x=-1$ $x=1$ точки экстремумов, список, множество
- $[-1]$ $f'\left(-1,1\right)>0$ $f'\left(-1\right)=0$ $f'\left(-0,9\right)<0$ знаки $f'(x)$ около $x=-1$
- $[1]$ $f'\left(0,9\right)>0$ $f'\left(1\right)=0$ $f'\left(1,2\right)<0$ знаки $f'(x)$ около $x=1$
- min $x=1$ точка минимума (переход ⇓, ⇑)
- max $x=-1$ точка максиума (переход ⇓, 0, ⇑)
Комментарии: 1. Надо найти производную функцию $f'\left(x\right)=\left(x^3-3x+2\right)'$ 2. уравнение, условие: производная = 0 3. Решить уравнение экстремумов, найти его корни, они же экстремумы 4. Исследовать функцию около точек экстремумов: взять точки чуть левее и чуть правее, Каковы знаки производных в этих точках?, функция возрастает, ⇑? или убывает ⇓ ? 5. Сделать выводы: точка экстремума является минимумом или максимумом? 6. Например, около точки $x=-1$ ситуация такая: при прохождении слева направо ... $x=-1,1;-1;-0,9$ ... производная $f'\left(x\right)$ "проходит" положительно, ноль, отрицательно. Тогда сама функция проходит как возрастает, остановка, убывает. Значит, $x=-1$ - точка максимума. 7. Итого: $x=-1$ точка максимума: слева интервал возрастания ⇑ , справа убывания ⇓. $x=1$ точка минимума: слева интервал убывания ⇓, справа возрастания ⇑ .
Задача 2: Найти min-max функции $f\left(x\right)=\left(x+2\right)^2\left(x-1\right)+1$
- $f\left(x\right)=\left(x+2\right)^2\left(x-1\right)+1$ функция
- $(\left(x+2\right)^2\left(x-1\right)+1)'=2\left(x+2\right)\left(x-1\right)+\left(x+2\right)^2=3x(x+2)$ - производная $f'\left(x\right)$ функции.
- $3x(x+2)=0$ $x=-2$ , $x=0$ - уравнение экстремума и его корни.
- $3x(x+2)>0$ $(-\infty;-2)+(0;+\infty)$ - производная $f'>0$ функция возрастает!
- $3x(x+2)<0$ $(-2;0)$ - производная $f'<0$ функция убывает!
- $X_f$ $x=-2$ $x=0$ - точки экстремума данной функции. Какой из них min? max?
- $M_f$ $x<-2$ $-2 < x<0$ $x>0$ Интервалы монотонности, все ...
- max $x=-2$ . до (слева) $x=-2$ возрастает ⇑, после (справа) убывает ⇓. Значит maximum
- min $x=0$ до (слева) $x=0$ убывает ⇓, после (справа) возрастает ⇑. Значит minimum
Комментарии: 1. Вычисляем производную 2. Составляем и решаем уравнение экстремумов 3. Указываем $X_f$ множество экстремумов, перечисляем все 4. Решаем неравенства производная > 0 и ... < 0 5. Перечисляем $M_f$ - все интервалы монотонности 6. Делаем выводы какой из экстремумов min, какой max в зависимости от переходов от ⇑ к ⇓ или наоборот.
Задача 5: Примеры нахождения точек минимума - максимума 3-х функций

Точки экстремумов функции, min-max, Наибольшее и наименьшее значение
Из $f'\left(x_0\right)\approx\frac{f\left(x_0+0,01\right)-f\left(x_0\right)}{x_0+0,01-x_0}$ выразим значение функции чуть правее точки $x_0$ : $f\left(x_0+0,01\right)\approx f\left(x_0\right)+0,01f'\left(x_0\right)$.
Значит, функция будет иметь большее значение правее от $x_0$ , если только $f'\left(x_0\right) > 0$.
Аналогичные рассуждения для значения функции чуть левее. Из $f'\left(x_0\right)\approx\frac{f\left(x_0-0,01\right)-f\left(x_0\right)}{x_0-0,01-x_0}$ $\Rightarrow$ $f\left(x_0-0,01\right)\approx f\left(x_0\right)-0,01\cdot f'\left(x_0\right)$ $\Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
Итак:
-
если $f'\left(x_0\right) > 0$ то $f\left(x_0-0,01\right) < f\left(x_0\right) < f\left(x_0+0,01\right)$ $\Rightarrow $ функция растет (см. слева направо).
-
если $f'\left(x_0\right) < 0$ то $f\left(x_0-0,01\right) > f\left(x_0\right) > f\left(x_0+0,01\right)$ $\Rightarrow $ функция убывает, график идет вниз.
-
если $f'\left(x_0\right)=0$ то ситуации более запутанные: при $f\left(x_0-0,01\right) < f\left(x_0\right) > f\left(x_0+0,01\right)$ точка $x=x_0$ называется точкой максимума. В нем функция "выше", чем по-соседству хоть слева, хоть справа.
В случае $f\left(x_0-0,01\right) > f\left(x_0\right) < f\left(x_0+0,01\right)$, $x=x_0$ - точка минимума. Если ни то, ни другое, то точка перегиба.
Определение: Точка, в которой производная обнуляется, называется экстремумом (минимум, максимум, перегиб). В этой точке наклон графика равен нулю, т.е. касательная к графику горизонтальна.
Точка максимума - если функция растет, "застывает" в $x_0$" , затем убывает. Производная функции больше нуля, в $x_0$ обнуляется, затем отрицательна.
Точка минимума наоборот - если функция убывает, "застывает" в $x_0$" , затем растет. Производная меньше нуля, равна нулю в $x_0$", затем положительна.
Нахождение точки минимума (максимума) функции $y=f\left(x\right)$:
Точка минимума - это $x$ - число, в котором производная равна нулю, а сама исходная функция от убывания переходит к возрастанию. Надо "взять" производную исходной функции и составить уравнение экстремума "производная равна нулю". Среди точек экстремума найти точку минимума.
Есть три способа:
- по поведению "рост / убывание" исходной функции ;
- либо поведение "отрицательности / положительности" производной;
- либо знак второй производной в этой точке; если 2-ая производная ("производная от производной") в точке $x_0$ положительна, то это минимум.
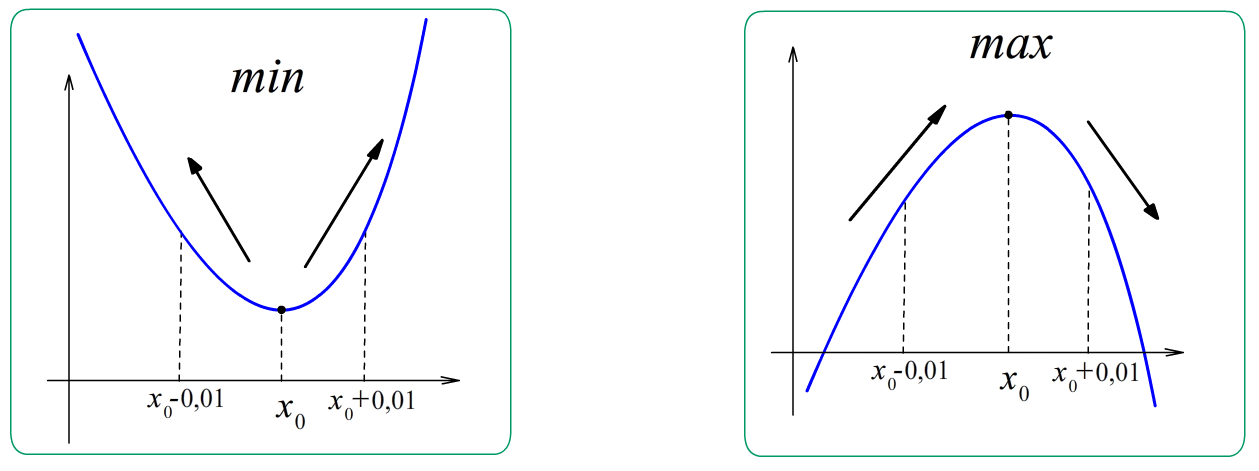
min: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) > f\left(x_0\right) < f\left(x_0+0,01\right)$ , $f'\left(x_0-0.01\right) < 0$ , $f'\left(x_0+0.01\right) > 0$ ; $f''\left(x_0\right) > 0$.
max: $f'\left(x_0\right)=0$ , $f\left(x_0-0,01\right) < f\left(x_0\right) > f\left(x_0+0,01\right)$ , $f'\left(x_0-0.01\right) > 0$ , $f'\left(x_0+0.01\right) < 0$ ; $f''\left(x_0\right) < 0$.
Пример 1: Найти точки экстремума функции $f\left(x\right)=x^3-3x+2$ . ;
- $f'\left(x\right)=\left(x^3-3x+2\right)'=3x^2-3$ находим производную от нашей функции
- $f'\left(x\right)=0$ $3x^2-3=0$ $x=1\ x=-1$ решаем уравнение экстремума
- Ранее мы нашли интервалы монотонности и знаем, где возрастание переходит в убывание и наоборот!
- $x=-1$ точка максимума: слева интервал возрастания, справа убывания
- $x=1$ точка минимума: слева интервал убывания, справа возрастания.
Нахождение наибольшего (наименьшего) значения функции $y=f\left(x\right)$ на указанном отрезке [ a ; b ] :
1) надо найти все точки экстремумов ("взять" производную, приравнять к нулю и найти корни);
2) выбрать среди точек экстремума те, которые окажутся "внутри отрезка" [ a ; b ];
3) вычислить в них значения исходной функции, вычислить также значения функции в концах отрезка. Среди полученных чисел выбрать наибольшее.
Точки - кандидаты на наибольшее : либо концы отрезка, либо экстремумы, попавшие в отрезок.
Пример 2: Найти наибольшее значение функции $y=\left(x+2\right)^2\left(x-1\right)+1$ на отрезке [-3 ; 0]
- $f'\left(x\right)=2\left(x+2\right)\left(x-1\right)+\left(x+2\right)^2$ - производная функции.
- $2\left(x+2\right)\left(x-1\right)+\left(x+2\right)^2=0$ - уравнение экстремума. Корни $x=-2$ , $x=0$.
- $x=-2$ и $x=0$ - точки экстремума данной функции.
- $f\left(-3\right)=-3$ $f\left(-2\right)=1$ $f\left(0\right)=-3$ - значения функции в концах и экстремумах.
- Наибольшее значение $y_{naibolshee}=1$ достигается в точке $x=-2$ .
Обозначения множеств, областей
- $D_f$ область определения функции
- $Z_f$ область знакопостоянства, интервалы положительности, отрицательности
- $M_f$ области монотонности функции, интервалы возрастания, убывания
- $X_f$ экстремумы функции, перечисление х - точек
- $T_f$ уравнение касательной к функции в указанной х - точке
- $E_f$ области значений функции, все у - значений
Упражнения (А):
Упражнения (В):
Задание №11 ЕГЭ, профиль: