
- Действия со степенями ·
- Преобразования числовых иррациональных выражений ·
- Преобразования числовых логарифмических выражений ·
- Вычисление значений тригонометрических выражений ·
- Преобразования числовых тригонометрических выражений
Действия со степенями
Формулы, свойства степеней:
- Умножение степеней - основание одинаковые, показатели складываются: $a^m\cdot a^n=a^{m+n}$ $\Leftrightarrow$ $a^{x+y}=a^x\cdot a^y$ ;
- $\frac{a^m}{a^n}=a^{m-n}$ $\Leftrightarrow$ $a^{x-y}=\frac{a^x}{a^y}$ Делении степеней с одинаковыми основаниями - основание прежнее, показатели вычитаются.
- $\left(a^x\right)^y=a^{xy}$ $\Leftrightarrow$ $a^{mn}=\left(a^m\right)^n$ Возведении степени в степень показатели перемножаются. И наоборот!
- $\left(a\cdot b\right)^x=a^x\cdot b^x$ $\Leftrightarrow$ $a^n\cdot b^n=\left(a\cdot b\right)^n$ Возведение в степень произведения - в эту степень возводится каждый множитель:
- $\left(\frac{a}{b}\right)^x=\frac{a^x}{b^x}$ $\Leftrightarrow$ $\frac{a^n}{b^n}=\left(\frac{a}{b}\right)^n$ Возведение в степень дроби в эту степень возводится числитель дроби и знаменатель . Деление?
- Дробная степень: $a^{\frac{x}{y}}=\left(\sqrt[y]{a}\right)^x$ ; $\sqrt[m]{a^n}=a^{\frac{n}{m}}$ Знаменатель как корень. Числитель как степень.
- Отрицательная степень $\Leftrightarrow$ обратная степень : $a^{-x}=\frac{1}{a^x}$ ; $\left(\frac{a}{b}\right)^{-x}=\left(\frac{b}{a}\right)^x$
Пример 1: Упростить $\frac{a^{-3}\cdot\left(3a^2b\right)^{-1}\cdot b^4}{\left(a^{-2}\right)^4\cdot b^{-2}}$
- по определению отрицательной, "перевернем" $\frac{\frac{1}{a^3}\cdot\frac{1}{3a^2b}\cdot b^4}{a^{-2\cdot4}\cdot\frac{1}{b^4}}$ , выполним деление, умножение дробей
- $\frac{b^4\cdot b^4}{a^{-8}\cdot a^3\cdot3a^2b}$ , умножим степени с одинаковыми основаниями $\frac{b^{4+4}}{a^{-8+3+2}\cdot3\cdot b}=\frac{b^8}{a^{-3}\cdot3\cdot b}$ , затем поделим степени
- с одинаковыми основаниями $\frac{b^{8-1}}{a^{-3}\cdot3}=\frac{b^7}{a^{-3}\cdot3}$ , еще раз "перевернем" отрицательную степень $\frac{a^3\cdot b^7}{3}$ .
Пример 2: Вычислить $\frac{2^{-11}\cdot4^6\cdot\left(0,5\right)^{-4}}{8^3\cdot\left(2^{-5}\right)^2}$
- Основания степеней переделаем на основание $2$: $4=2^2$ $8=2^3$ $0,5=2^{-1}$
- $\frac{2^{-11}\cdot4^6\cdot\left(0,5\right)^{-4}}{8^3\cdot\left(2^{-5}\right)^2}=\frac{2^{-11}\cdot\left(2^2\right)^6\cdot\left(2^{-2}\right)^{-4}}{\left(2^3\right)^3\cdot\left(2^{-5}\right)^2}$ степень в степени? преобразуем как произведение показателей
- $=\frac{2^{-11}\cdot2^{12}\cdot2^8}{2^9\cdot2^{-10}}=$ Умножение степеней? ... равно через сложение показателей
- $=\frac{2^{-11+12+8}}{2^{9-10}}=\frac{2^9}{2^{-1}}=$ Упростим показатели в числителе и знаменателе
- Деление степеней и вычисление 10-ой степени: $=\frac{2^9}{2^{-1}}=2^{9-\left(-1\right)}=2^{10}=1024$
- $\frac{2^{-11}\cdot4^6\cdot\left(0,5\right)^{-4}}{8^3\cdot\left(2^{-5}\right)^2}=\frac{2^{-11}\cdot\left(2^2\right)^6\cdot\left(2^{-2}\right)^{-4}}{\left(2^3\right)^3\cdot\left(2^{-5}\right)^2}=\frac{2^{-11}\cdot2^{12}\cdot2^8}{2^9\cdot2^{-10}}=\frac{2^{-11+12+8}}{2^{9-10}}=\frac{2^9}{2^{-1}}=2^{9-\left(-1\right)}=2^{10}=1024$
Пример 3: Вычислить $\frac{15^{18}:\left(5^{16}-16\cdot15^{14}\right)}{\left(15+30\right)^3}$
- вынесем за скобки $14$ -ую степень $\frac{15^{18}:5^{14}\cdot\left(5^2-16\right)}{45^3}$ . выполним деление степеней и разложим основание
- в знаменателе $\frac{15^{18-14}\cdot\left(25-16\right)}{\left(15\cdot3\right)^3}$ . используя свойство произведения степеней и правило сокращения дробей
- упростим выражение $\Rightarrow $ $\frac{15^4 \cdot 9}{15^3 \cdot 3^3}=\frac{15^1\cdot3^2}{3^3}=\frac{15}{3}=5$ .
Преобразования числовых иррациональных выражений
Свойства радикалов:
- $\left(\sqrt{a}\right)^2=a$ ; $\sqrt{a^2}=a$ - основные тождества . $\sqrt{9}\ne-3$ $\sqrt{a^4}=a^2$
- $\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}$ $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$
- $\sqrt{a^2\cdot b}=a\cdot\sqrt{b}$ - вынос квадратного множителя за знак радикала, частичное извлечение корня $\sqrt{\frac{a}{b^2}}=\frac{\sqrt{a}}{b}$
- $\sqrt{a^4}=a^2$ $\sqrt{a^{12}}=a^6$ $\sqrt{a^{2n}}=a^n$ $\left(\sqrt[n]{a}\right)^n=a$
- $\sqrt[n]{a\cdot b}=\sqrt[n]{a}\cdot\sqrt[n]{b}$ $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ $\sqrt[3]{b\cdot a^3}=a\cdot\sqrt[3]{b}$ $\sqrt[n]{b\cdot a^n}=a\cdot\sqrt[n]{b}$
- $\sqrt{a+\sqrt{b}}=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}+\sqrt{\frac{a-\sqrt{a^2-b}}{2}}$ Формулы сложного радикала $\sqrt{a-\sqrt{b}}=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}-\sqrt{\frac{a-\sqrt{a^2-b}}{2}}$
Полезные Навыки, действия с квадратными радикалами:
-
"Радикал от умножения" равен умножению радикалов. "Радикал от деления" равен делению радикалов. "Радикал от квадрата положительного числа" равен самому числу. "Радикал от степени" - степень с половиной показателя. "Вынос квадрата за радикал" - если внутри радикала есть множитель - квадрат числа, то само число выносится вперед радикала. Если внутри радикала есть два одинаковых множителя (квадрат?), то множителем впереди радикала выносим один из них. Для упрощения радикала подрадикальное число или выражение удобно разлагать на множители, желательно в виде полных квадратов.
-
Корень из умножения равно умножению корней. Произведение корней равен корню из произведения. Корень деления равен делению корней. Если делится двя корня, то это тоже самое, что под корнем поставить деление. Если под корнем есть квадратный множитель, то ее без квадрата можно вынести за знак корня. Корень из трех множителей превращается в умножение трех корней из каждого множителя. Упростить радикал - под корнем разложить на множители, обнаружить полные квадраты и частично извлекать корни. Упростить умножение или деление радикалов - "загнать" все множители, делители под крышей одного радикала и упрощать. корень из произведения равен умножению корней; корень из отношения равен делению корней; вынос полного куба из под кубического радикала; вынос полной степени того же порядка, что и корень, за знак корня.
Пример 4: Вычислить, преобразовать выражения, содержащие числовые радикалы:
- $\sqrt{729}=27$ $\sqrt{48}\cdot\sqrt{12}\cdot\sqrt{75}=\sqrt{48\cdot12\cdot75}=\sqrt{8\cdot6\cdot2\cdot6\cdot3\cdot25}=6\cdot5\cdot\sqrt{16\cdot3}=120\sqrt{3}$
- $\sqrt{75}=\sqrt{3\cdot25}=\sqrt{3}\cdot\sqrt{25}=5\sqrt{3}$ $\sqrt{2^2\cdot3\cdot7^2\cdot6}=2\cdot7\cdot\sqrt{3\cdot3\cdot2}=2\cdot7\cdot3\cdot\sqrt{2}=42\sqrt{2}$
- $\sqrt{0.81}=\sqrt{\frac{81}{100}}=\frac{\sqrt{81}}{\sqrt{100}}=\frac{9}{10}=0.9$ $\sqrt{\frac{64}{225}}=\frac{\sqrt{64}}{\sqrt{225}}=\frac{8}{15}$
- Действия: .... под корнем разложили на множители, увидели полный квадрат числа, извлекли; .... вынос корня по частям от множителей - полных квадратов; Числа без квадратов "выходят" вперед. .... "если внутри квадрата два одинаковых множителя, из двух выносим один вперед". .... десятичное число превратили в дробное , использовали свойство радикала от деления; .... свойство радикала от деления: нашли дробь, квадрат которой будет подрадикальной дробью.
Пример 5: Упростить иррациональные выражения
- $\left(\sqrt{98}-\sqrt{6}\right)\sqrt{8}=\sqrt{98}\cdot\sqrt{8}-\sqrt{6}\cdot\sqrt{8}=\sqrt{98\cdot8}-\sqrt{6\cdot8}=\sqrt{49\cdot2\cdot8}-\sqrt{3\cdot16}=7\cdot4-4\sqrt{3}=28-4\sqrt{3}$
- Правила перемножения скобки на число или скобку: каждое слагаемое одной скобки умножается на каждое слагаемое другой
- $\left(3\sqrt{10}-4\sqrt{2}\right)\left(-6\sqrt{5}+8\right)=-3\sqrt{10}\cdot6\sqrt{5}+3\sqrt{10}\cdot8+4\sqrt{2}\cdot6\sqrt{5}-4\sqrt{2}\cdot8=-18\sqrt{2\cdot5\cdot5}+24\sqrt{10}+24\sqrt{2\cdot5}-32\sqrt{2}=-90\sqrt{2}+48\sqrt{10}-32\sqrt{2}=48\sqrt{10}-122\sqrt{2}$
- $\left(5\sqrt{8}-\sqrt{73}\right)\left(\sqrt{73}+5\sqrt{8}\right)=\left(5\sqrt{8}\right)^2-\left(\sqrt{73}\right)^2=25\cdot8-73=77$ ... разность квадратов?
- Использовано формула $\left(a-b\right)\left(a+b\right)=a^2-b^2$ Здесь: $a=5\sqrt{8}$ $b=\sqrt{73}$ и $\left(\sqrt{x}\right)^2=x$
Преобразования числовых логарифмических выражений
Формулы, свойства логарифмов
- Что такое Логарифм $\log_48$ ? это просто число $\frac{3}{2}$ . Потому что, если $4$ возвести в степень $\frac{3}{2}$ , то получится $8$ .
- Определение Логарифма: $\log_ab$ -- показатель той степени, в которую надо возвести $a$ чтобы получить $b$.
- Основное тождество: $a^{\log_ab}=b$ $a$ - основание , $b$ - аргумент, $\log_ab$ - показатель степени.
- Основное тождество $\log_ab=n$ $\Leftrightarrow$ $b=a^n$ $a^{\log b_a}=b$ Логарифм есть показатель степени!
- сумма логарифмов $\log_ax+\log_ay=\log_axy$ логарифм произведения. разность логарифмов $\log_ax-\log_ay=\log_a\frac{x}{y}$
- формула замены основания: $\log_ab=\frac{1}{\log_ba}$ обратное логарифма $\frac{1}{\log_ba}=\log_ab$
- Вынос показателя степени аргумента: $\log_a\left(b^c\right)=c\cdot\log_ab$ ; и наоборот: множитель заносится внутрь $c\cdot\log_ab=\log_a\left(b^c\right)$
- Вынос показателя степени основания: $\log_{\left(a^n\right)}b=\frac{1}{n}\cdot\log_ab$ ; множитель заносится как корень основания $n\cdot\log_ab=\log_{\left(a^{\frac{1}{n}}\right)}b$
- Переход к новому основанию: $\log_ab=\frac{\log_xb}{\log_xa}$ ; отношение двух логарифмов с одинаковым основанием $\frac{\log_xb}{\log_xa}=\log_ab$
- Перекрестное произведение логарифмов: $\log_ax\cdot\log_xb=\log_ab$ ; аргумент одного равен основанию другого, как будто "сокращение" .
- Универсальная формула для степеней внутри логарифма: $\log_{\left(a^n\right)}\left(b^m\right)=\frac{m}{n}\cdot\log_ab$ ;
- Транзит, логарифм в показателе: $a^{\log_xb}=b^{\log_xa}$ $2^{\log_83}=3^{\log_82}$
- Инверсия степени: $\log_213$ - это то число-показатель, в которую надо возвести $2$ чтоб получить $13$, т.е. $2^{\log_213}=13$
- Аналогия: $\sqrt{13}$ - это то число, чей квадрат станет $13$, т.е. $\left(\sqrt{13}\right)^2=13$
- Аналогия: $\sqrt[4]{13}$ это то число, чья $4$-ая степень даст $13$, т.е. $\left(\sqrt[4]{13}\right)^4=13$
- Аналогия: $\arcsin\left(\frac{1}{3}\right)$ это число, чей синус $\frac{1}{3}$, т.е. $\sin\left(\arcsin\frac{1}{3}\right)=\frac{1}{3}$
- $\lg a=\log_{10}{a}$ - десятичный логарифм $\lg 0,001=-3$ $\ln a=\log_ea=\log_{2,71..}{a}$ - натуральный логарифм
Пример 6: Вычислить числовые логарифмы:
- $\log_381=?$ так, как $3^4=81$ то $\log_381=4$ $\log_{2}{2^5}=5$ т.к. $2^5=2^5$
- $2^{\log_28}=8$ $2^{\log_27}=7$ $2^{\log_2{13}}=13$ $2^{\log_2a}=a$
- $2^{\log_{2}{7}+\log_{2}{8}}=2^{\log_{2}{7}} \cdot 2^{\log_{2}{8}}=7\cdot 8$ $2^{\log_{2}{x}+\log_{2}{y}}=2^{\log_{2}{x}} \cdot 2^{\log_{2}{y}}=x\cdot y$ $2^{\log_2{(7\cdot 8})}=7\cdot 8$ $2^{\log_2{(x\cdot y)}}=x\cdot y$
- $\log_{0.125}4=?$ т.к $0.125^{-\frac{2}{3}}=4$ получаем $\log_{0.125}4=-\frac{2}{3}$
- $\lg0.0001=?$ так, как $10^{-4}=0.0001$, получаем десятичный логарифм $\lg0.0001=-4$
- $\log_{36}6\sqrt{6}=?$ так, как $36^{\frac{3}{4}}=\left(\sqrt{6}\right)^3=6\sqrt{6}$ значит, $\log_{36}6\sqrt{6}=\frac{3}{4}$
- $\log_{\sqrt[5]{3}}\left(\sqrt[4]{9}\right)=\log_{\left(3^{\frac{1}{5}}\right)}\left(9^{\frac{1}{4}}\right)=\frac{1}{\frac{1}{5}}\cdot\log_3\left(9^{\frac{1}{4}}\right)=5\cdot\frac{1}{4}\cdot\log_39=5\cdot\frac{1}{4}\cdot2=2,5$ ... корень в дробную степень. вынос показателей.
Пример 7: Вычислить $\left(\frac{1}{9}\right)^{\log_{\frac{1}{3}}13}$ перестановочность показателей $\left(a^x\right)^y=a^{x\cdot y}=\left(a^y\right)^x$
- основание степени $\frac{1}{9}$ , основание логарифма $\frac{1}{3}$ . преобразуем первое в квадрат второго $\left(\left(\frac{1}{3}\right)^2\right)^{\log_{\frac{1}{3}}13}$
- формула степень в степени приводит к умножению в показателе $\left(\frac{1}{3}\right)^{2\cdot\log_{\frac{1}{3}}13}$ но, те же множители $x\equiv2$ и $y\equiv\log_{\frac{1}{3}}13$
- могут составить другую комбинацию степень в степени, $\left(\left(\frac{1}{3}\right)^{\log_{\frac{1}{3}}13}\right)^2$ основное тождество $\left(13\right)^2=169$
Пример 8: Упростить: $\left(\sqrt{7}\right)^{4+\log_{\sqrt{7}}0,5}$ разделение показателей $z^{a+\lg b}=z^a\cdot z^{\lg b}$
- в показателе сумма чисел, обычного и логарифмического $\left(\sqrt{7}\right)^4\cdot\left(\sqrt{7}\right)^{\log_{\sqrt{7}}0,5}$ упростим, $49\cdot0,5=24,5$
Пример 9: Еще преобразования:
- $\frac{\log_{\frac{2}{3}}36}{\log_{\frac{2}{3}}216}=\log_{216}36=\log_{6^3}\left(36\right)=\frac{1}{3}\cdot\log_636=\frac{1}{3}\cdot\log_6\left(6^2\right)=\frac{2}{3}\cdot\log_66=\frac{2}{3}$
- $\lg300+\lg0.3=\lg\left(3\cdot100\right)+\lg\left(\frac{3}{10}\right)=\lg3+\lg100+\lg3-\lg10=2\lg3+2-1=2\lg3+1$
Пример 10: Еще примеры на преобразования, поэтапное применения формул, упрощения:
- формула для дробного множителя $a^{\frac{1}{n}\lg b}=\left(a^{\frac{1}{n}}\right)^{\lg b}=\left(\sqrt[n]{a}\right)^{\lg b}$
- $81^{\frac{1}{4}\log_{27}49}=\left(81^{\frac{1}{4}}\right)^{\log_{3^3}49}=\left(\sqrt[4]{81}\right)^{\frac{1}{3}\cdot\log_349}=3^{\log_349^{\frac{1}{3}}}=3^{\log_37^{\frac{2}{3}}}=7^{\frac{2}{3}}=\sqrt[3]{49}$
- комментарий: в показателе произведение дробного и логарифмических чисел. превратим в "степень степени". .....дробную $\frac{1}{4}$ степень представим в виде радикала и вычислим. ....из основания логарифма вынесем показатель $3$ в виде $\frac{1}{3}$ вперед....из аргумента логарифма вынесем показатель $2$ , превратим аргумент в $7$ .... Теперь, в логарифм от $7$ занесем $\frac{1}{3}$ внутрь логарифма как степень..... Основное тождество "упразднит" логарифм при одинаковых основаниях.
- $\left(\sqrt[4]{25^{\log_510}-7^{\log_719}}\right)=\sqrt[4]{5^{2\cdot\log_510}-19}=\sqrt[4]{5^{\log_5100}-19}=\sqrt[4]{100-19}=\sqrt[4]{81}=81^{\frac{1}{4}}=3$
- постепенно разбираемся внутри радикала, упрощаем по свойствам логарифма. учтем что $25$ степень $5$ .
- $\frac{2\log_{0.6}3+\log_{0,6}\sqrt{3}}{\log_{0,6}3-\log_{0,6}\sqrt{3}+\log_{0.6}9}=\frac{\log_{0.6}9+\log_{0,6}\sqrt{3}}{\log_{0,6}\left(\frac{3}{\sqrt{3}}\right)+\log_{0.6}9}=\frac{\log_{0.6}\left(9\sqrt{3}\right)}{\log_{0,6}\left(\sqrt{3}\right)+\log_{0.6}9}=\frac{\log_{0.6}\left(9\sqrt{3}\right)}{\log_{0,6}\left(\sqrt{3}\cdot9\right)}=\log_{9\sqrt{3}}\left(9\sqrt{3}\right)=1$
- чтобы сложить логарифмы, нужно избавиться от множителей впереди. значит, надо "занести" их внутрь логарифма как показатель. разбираемся с числителем и знаменателем по отдельности, по формулам суммы/разности логарифмов.


Вычисление значений тригонометрических выражений
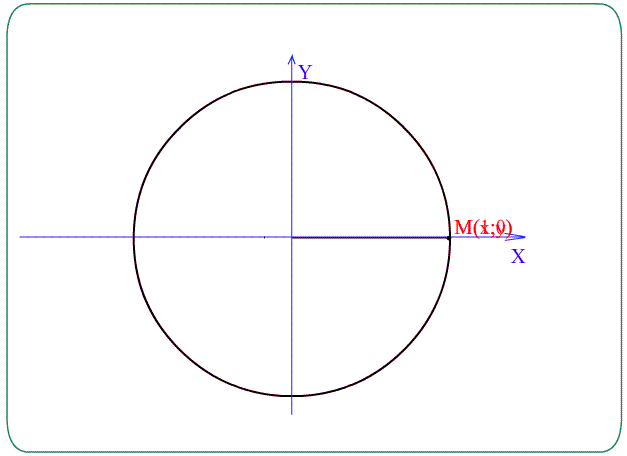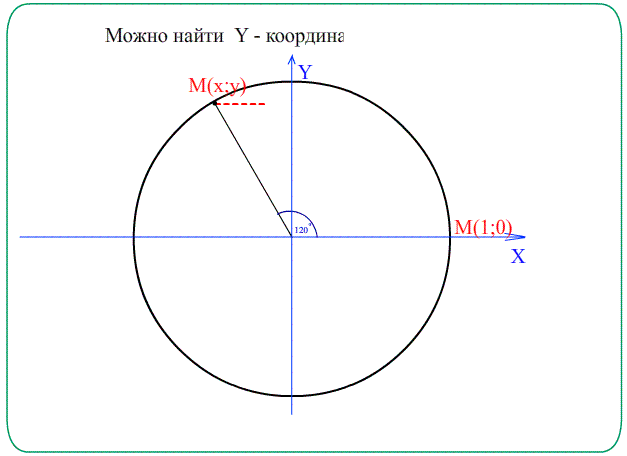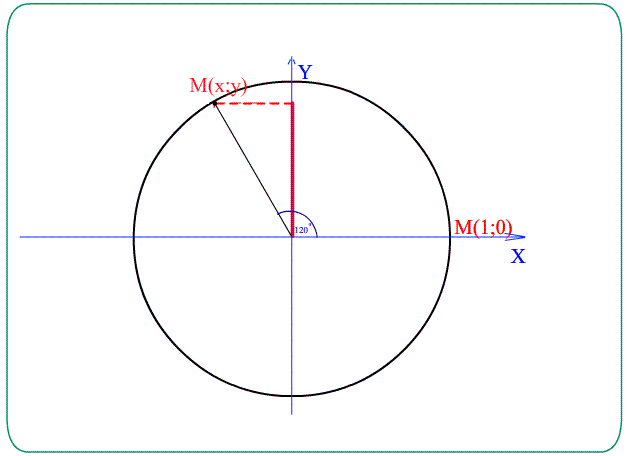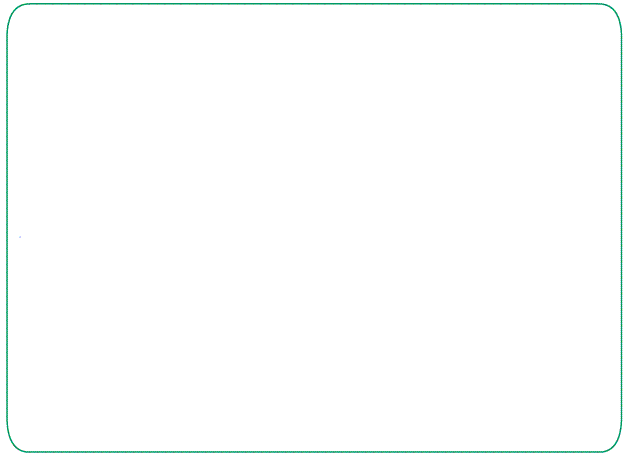
- Каждому углу $\left(t\right)$ , или числу $t$ - радиан соответствует точка $M\left(t\right)$ на Е.Т.О. $x$ - абсциссой и $y$ - ординатой точки.
- Синус угла $t$ - это $y$ - координата соответствующей точки $M\left(t\right)$ на Е.Т.О : $\sin t=y$ $M\left(t\right)=\left(x;y\right)$
- Косинус угла $t$ - это $x$ - координата соответствующей точки $M\left(t\right)$ на Е.Т.О : $\cos t=x$ $M\left(t\right)=\left(x;y\right)$
- Тангенс угла $t$ - это отношение $y$ - координаты к $x$ - координате соответствующей точки $M\left(t\right)$ на Е.Т.О $\tg t=\frac{y}{x}$
- Котангенс угла $t$ - это отношение $x$ - координаты к $y$ - координате соответствующей точки $M\left(t\right)$ на Е.Т.О $\ctg t=\frac{x}{y}$
- Е.Т.О. разбивается на $4$ четверти. Для всех точек на окружности координаты $-1\le x\le1$ $-1\le y\le1$
- Знаки координат определяются по четвертям. Например, в третьей четверти обе координаты отрицательные.
- Значит, знаки синуса и косинуса зависят от того, в какую четверть попадает соответствующая точка.
- Радиус Е.Т.О. равен $1$ . значит, ни абсцисса, ни ордината не превосходят по модулю $1$: $\left|\sin t\right|\le1$ $\left|\cos t\right|\le1$
- $x^2+y^2=1$ для всех точек на Е.Т.О. $\Leftrightarrow$ теорема Пифагора $\sin^2t+\cos^2t=1$ для любого $a$.
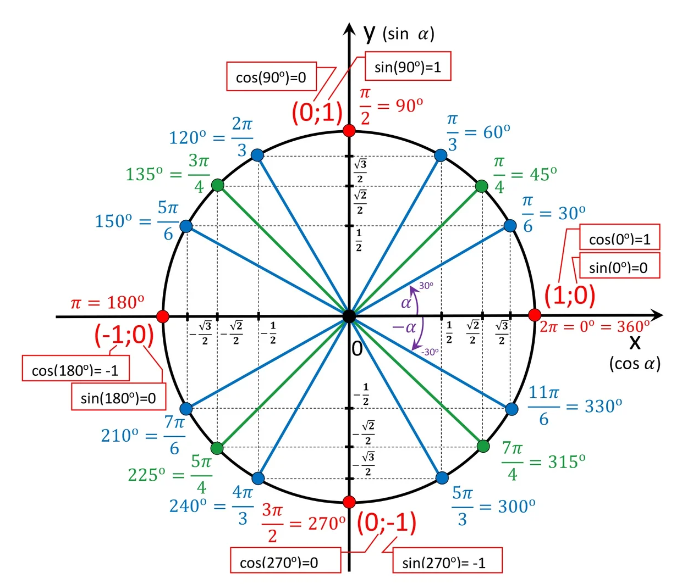
Калькуляторы: как находить приближенные значения $sin$ и $cos$ произвольного угла в градусах и в радианах:

Формула приведения "для градусов":
- Путем выделения 90 - кратных добавок функцию от большого угла можно привести к функции малого угла, меньше 90 градусов.
- $trig\left(\pm180\cdot m\pm A\right)=\left(?\right)trig\left(A\right)$ , где $m$ - целое. Четно - $90$ -кратные добавки функцию не меняют.
- $trig\left(\pm90\cdot n\pm A\right)=\left(?\right)cotrig\left(A\right)$ , где $n$ - нечетное целое. Нечетно - $90$ -кратные добавки меняют на "сопряженную".
- В формуле вместо (?) впереди ставится знак исходной функции в той четверти, в которой попадает большой угол.
- Алгоритм: 1) определяем знак функции по четверти 2) выделяем 90-кратную добавку от малого угла 3) функцию ставим по чет-нечет.
Пример 12: Преобразовать выражения с помощью формул приведения:
- Дополнение угла до 90 градусов, смена: $\sin68=\sin\left(90-22\right)=\cos22$ $\tg53=\tg\left(90-37\right)=\ctg37$
- $\sin330=$ выделим 90-добавки $=\sin\left(4\cdot90-30\right)=$ в IV-ой знак sin "-", 4-кратное $90$ не меняет sin: $\sin330=-\sin30=-\frac{1}{2}$
- $\sin330=$ выделим 90-добавки $=\sin\left(3\cdot90+60\right)=$ в IV-ой знак sin "-", 3-кратное $90$ sin меняет на cos: $\sin330=-\cos60=-\frac{1}{2}$
- $\cos234=\cos\left(2\cdot90+54\right)=-\cos54$ III четверть, знак cos "-", четная 2-крат добавка - cos не меняется.
- $\tg510=\tg\left(5\cdot90+60\right)=-\ctg60=-\frac{\cos60}{\sin60}=-\frac{1}{\sqrt{3}}$ II четверть, знак tg "-", нечетная 5-крат добавка - tg меняется на ctg.
- $\ctg298=\ctg\left(3\cdot90+28\right)=-\ctg28$ $\cos510=\cos\left(5\cdot90+60\right)=-\sin30=-0,5$
Основные тригонометрические тождества:
- Теорема Пифагора: $\sin^2a+\cos^2a=1$ $\cos a=\pm\sqrt{1-\sin^2a}$ $\sin a=\pm\sqrt{1-\cos^2a}$
- Свойства (ко-) тангенса: $\tg a=\frac{\sin a}{\cos a}$ $\ctg a=\frac{\cos a}{\sin a}$ $\tg a\cdot\ctg a=1$
- Смена функции, $90^o$ - дополнение: $\sin a=\cos\left(90^o-a\right)$
- Смена функции, $90^o$ - дополнение: $\cos a=\sin\left(90^o-a\right)$ $trig\left(a\right)=cotrig\left(90-a\right)$
- Смена функции, $90^o$ - дополнение: $\tg a=\ctg\left(90^o-a\right)$
- Формулы двойнных углов $ \sin2x=2\cdot\sin x\cdot\cos x $ $\tg2x=\frac{2\cdot\tg x}{1-\tg^2x}$ $\ctg2x=\frac{\ctg^2x-1}{2\cdot\ctg x}$
- $\cos2x=\cos^2 x-\sin^2x$ $\cos2x=2\cdot\cos^2x-1$ $\cos2x=1-2\cdot\sin^2x$
Пример 12: Преобразовать выражения, применив тождества, формулы приведения, значения хороших углов:
- $8\cdot\sin330\cdot\cos510=8\cdot\sin\left(4\cdot90-30\right)\cdot\cos\left(5\cdot90+60\right)=8\cdot\left(-\sin30\right)\cdot\left(-\cos60\right)=8\cdot\left(-0,5\right)\cdot\left(-0,5\right)=2$
- $5\cdot\ctg297\cdot\tg63=5\cdot\ctg\left(3\cdot90+27\right)\cdot\tg63=5\cdot\left(-\tg27\right)\cdot\tg\left(90-27\right)=5\cdot\left(-\tg27\right)\cdot\ctg27=-5$
- $12\sqrt{3}\tg\left(-210\right)=?$ $\tg\left(-210\right)=\tg\left(-2\cdot90-30\right)=+\tg30=\frac{\sqrt{3}}{3}$ $12\sqrt{3}\tg\left(-210\right)=12\sqrt{3}\cdot \frac{\sqrt{3}}{3}=12$
- $9\cdot\tg305\cdot\tg215=9\cdot\tg\left(3\cdot90+35\right)\cdot\tg\left(2\cdot90+35\right)=9\cdot\left(-\ctg\left(35\right)\right)\cdot\left(+\tg\left(35\right)\right)=-9\cdot\ctg\left(35\right)\cdot\tg\left(35\right)=-9$
- $\sin225\cdot\cos330=\sin\left(2\cdot90+45\right)\cdot\cos\left(3\cdot90+60\right)=\left(-\sin45\right)\cdot\left(+\sin60\right)=\left(-\frac{\sqrt{2}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=-\frac{\sqrt{6}}{4}$
- $\frac{\sin\left(-15\right)\cdot\ctg\left(-15\right)}{\cos\left(345\right)\cdot\tg\left(195\right)}=\frac{-\sin15\cdot\left(-\ctg15\right)}{\cos\left(360-15\right)\cdot\tg\left(180+15\right)}=\frac{\sin15\cdot\frac{\cos15}{\sin15}}{\cos15\cdot\tg15}=\frac{\cos15}{\cos15\cdot\frac{\sin15}{\cos15}}=\ctg15$
- $\tg1620-\sin675+\cos765=\tg\left(1800-180\right)-\sin\left(720-45\right)+\cos\left(720+45\right)=0+\sin45+\cos45=\sqrt{2}$
- $\frac{\ctg t-1}{1-\tg t}=\frac{\frac{\cos t}{\sin t}-1}{1-\frac{\sin t}{\cos t}}=\frac{\cos t\cdot\left(\cos t-\sin t\right)}{\sin t\cdot\left(\cos t-\sin t\right)}=\frac{\cos t}{\sin t}=\ctg t$
Пример 13: Найдите $\tg a$ если $\sin a=-\frac{2\sqrt{6}}{5}$ и угол из интервала $180<a<270$
- этот угол в III-ей четверти. Там и х - координата и у - координата отрицательные.
- Значит и синус и косинус - отрицательные. А вот тангенс и котангенс III-ей четверти положительные.
- Косинус найдем из формулы $\cos a=\pm\sqrt{1-\sin^2a}=\pm\sqrt{1-\left(-\frac{2\sqrt{6}}{5}\right)^2}=\pm\frac{1}{5}$
- Надо выбрать отрицательное $\cos a==-\frac{1}{5}$. находим тангенс по формуле $\tg a=\frac{\sin a}{\cos a}=\frac{-\frac{2\sqrt{6}}{5}}{-\frac{1}{5}}=2\sqrt{6}$


Упражнения:
